평면에서 가운데 점을 중심으로 같은 거리만큼 떨어진 점들로 이루어진 도형이다.
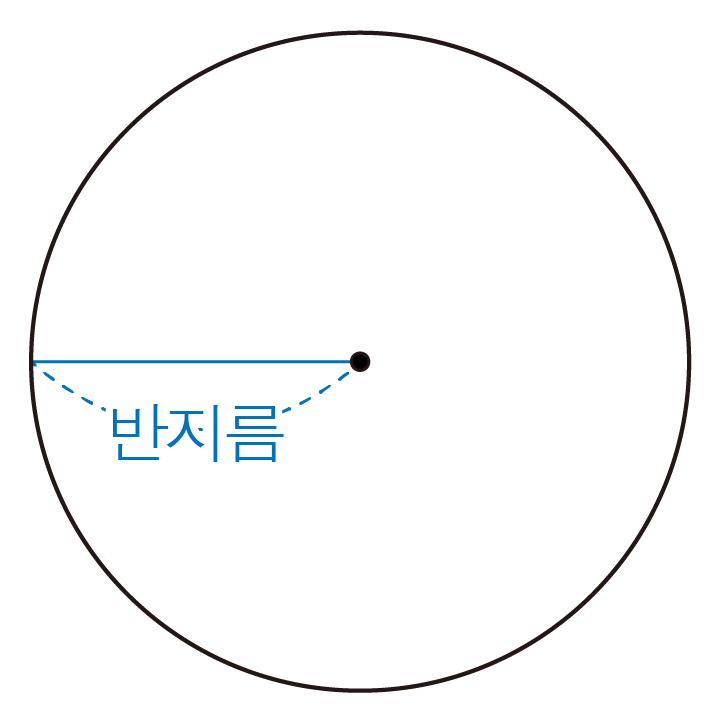
원 위의 한 점에서 원의 중심까지의 거리이다.
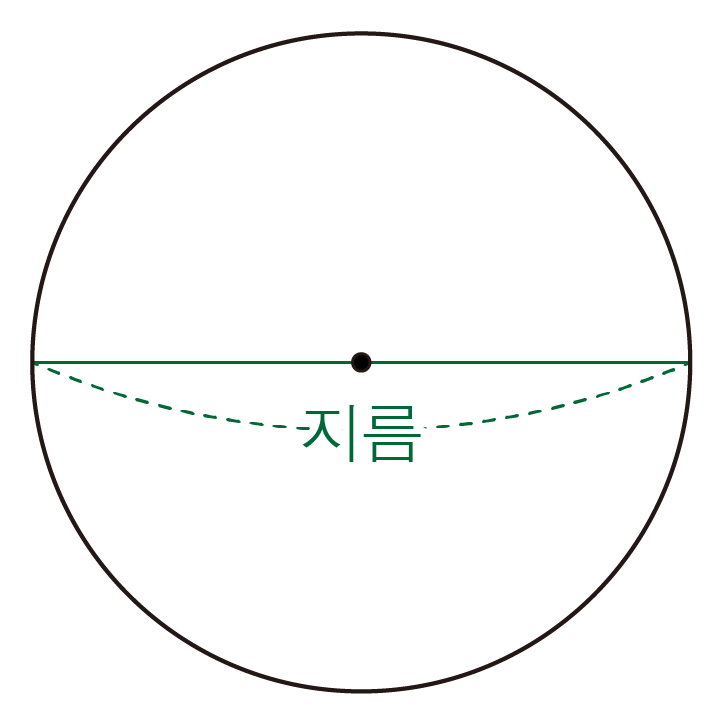
원 위의 한 점에서 중심을 지나 반대편까지의 직선 거리이다. 지름은 반지름의 2배와 같다.
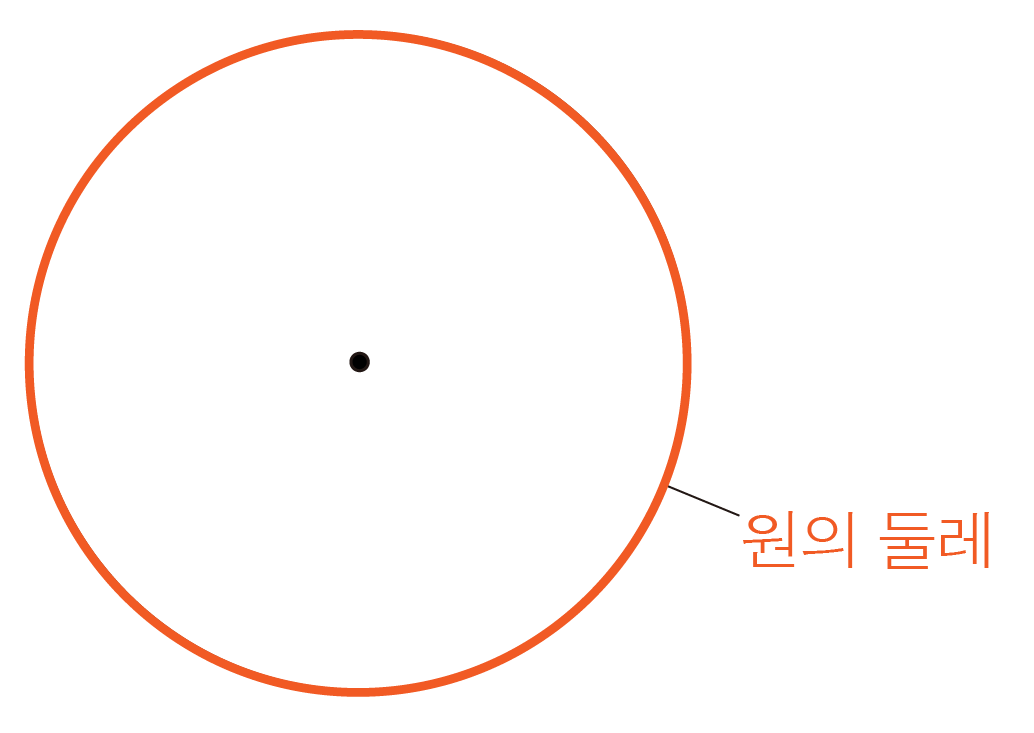
원의 바깥선을 따라 한 바퀴 돌아 잰 길이이다.
원의 둘레를 지름으로 나눈 값이다. 지름원의둘레=3.141592⋯의 값을 가지며, 기호로 π로 나타낸다. π는 ‘파이’로 읽는다.
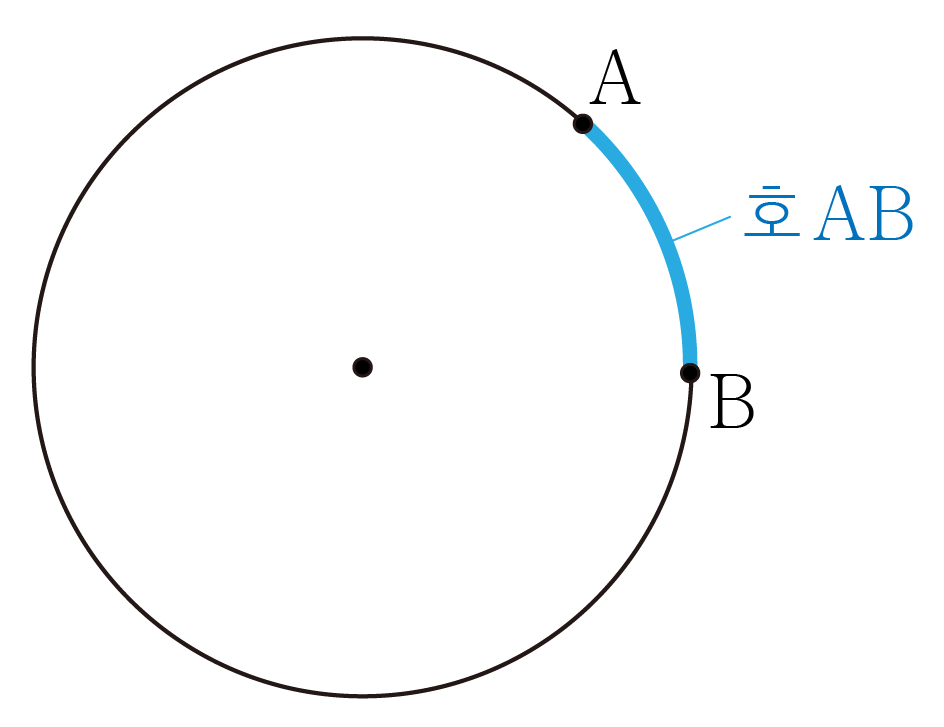
원의 둘레의 일부이다.
두 직선이나 면이 벌어진 정도를 나타낸 것이다. '도'와 '라디안'을 통해 표현한다.
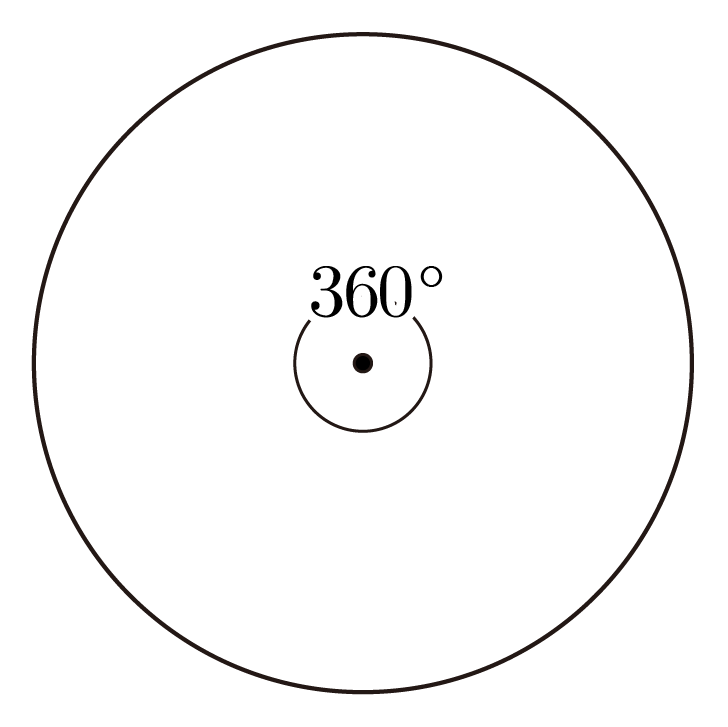
원을 한 바퀴 도는 각도를 360∘로 하여 나타낸 것이다. 기본 단위는 도(∘)이다.
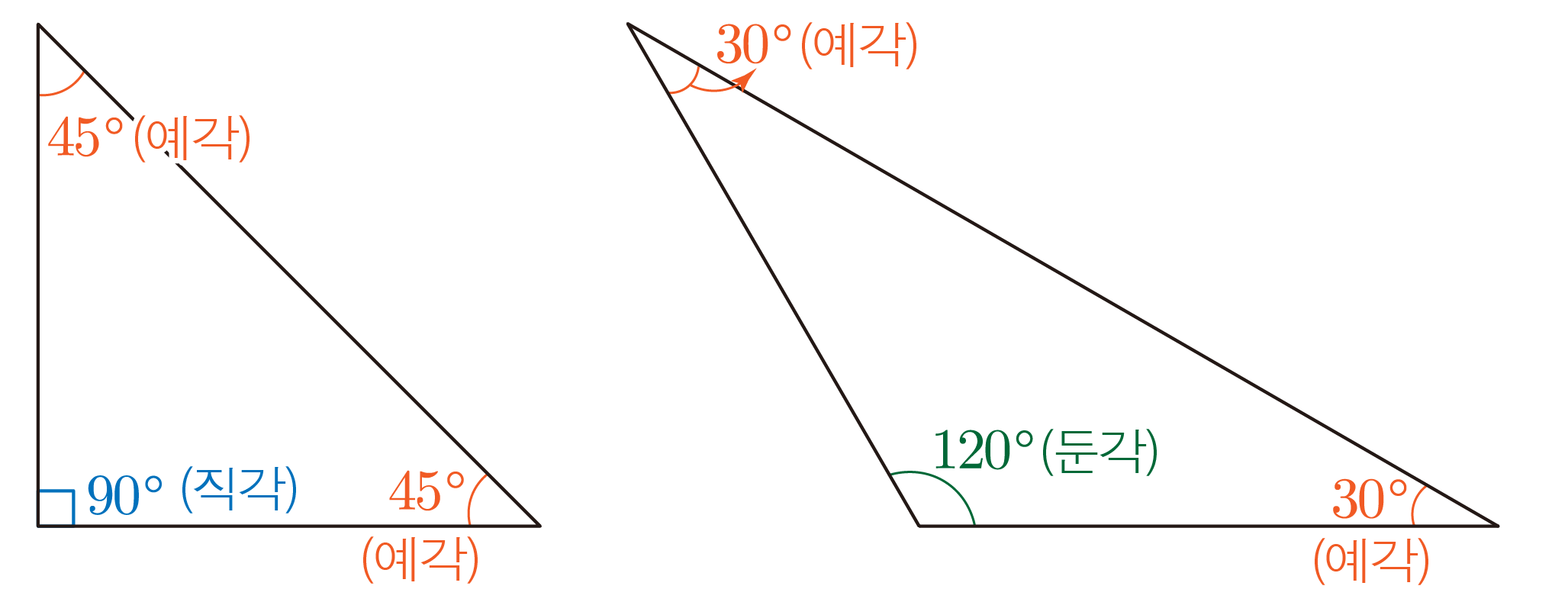
90∘는 직각, 90∘보다 작은 각은 예각, 90∘보다 크고 180∘보다 작은 각은 둔각이라 한다.
직각은 보통 작은 네모를 그려 나타낸다.
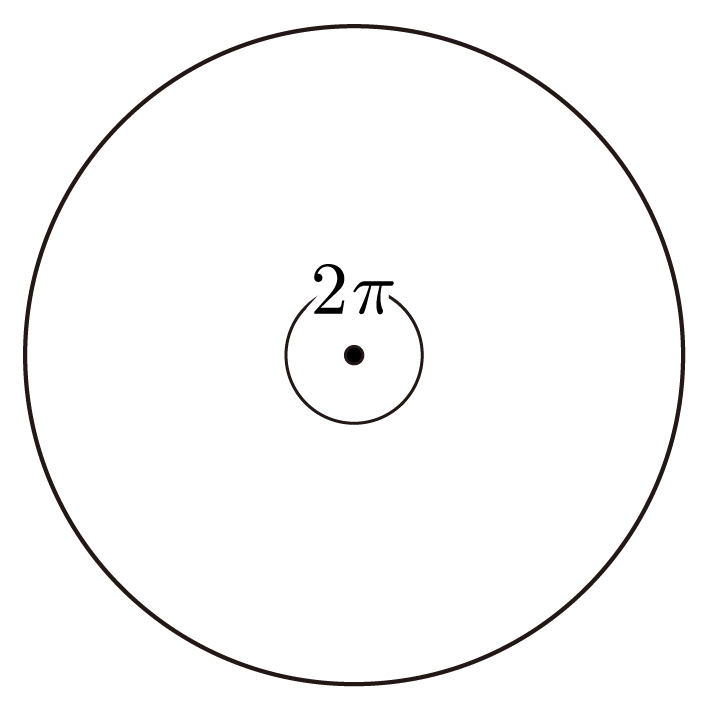
π를 통해 나타낸 각도이다. 기본 단위는 rad이고, 도(∘)와 달리 단위를 생략할 수 있다. 360∘는 2πrad과 같다.
도에서 라디안으로 변환할 때:
라디안=도$\times\frac{\pi\thinspace\mathrm{rad}}{180^\circ}$
라디안에서 도로 변환할 때:
도=라디안×πrad180∘
120∘를 라디안으로 변환해보자.
라디안=도×180∘πrad이므로 120∘×180∘πrad=32πrad=32π(rad은 생략 가능)이다.
23πrad을 도로 변환해보자.
도=라디안×πrad180∘이므로 23πrad×πrad180∘=270∘이다.
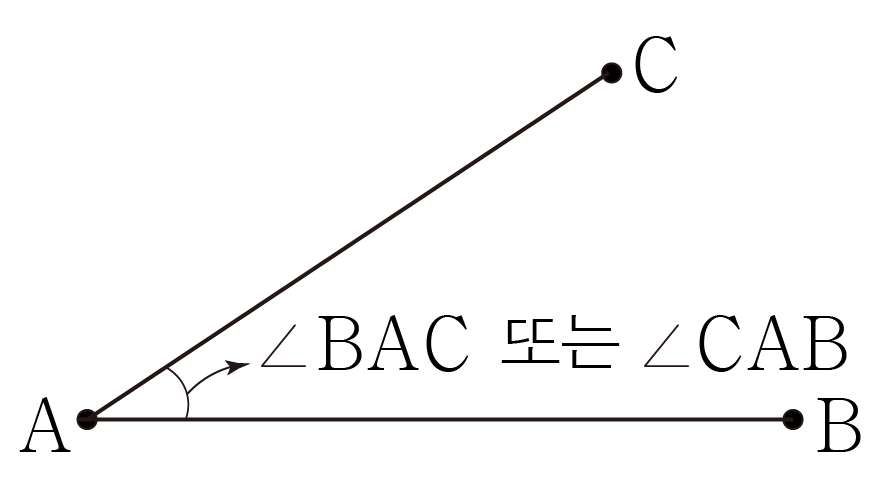
아래 그림과 같이 선 AB와 선 AC 사이의 각도를 나타내는 경우 ∠CAB 또는 ∠BAC로 표기한다.
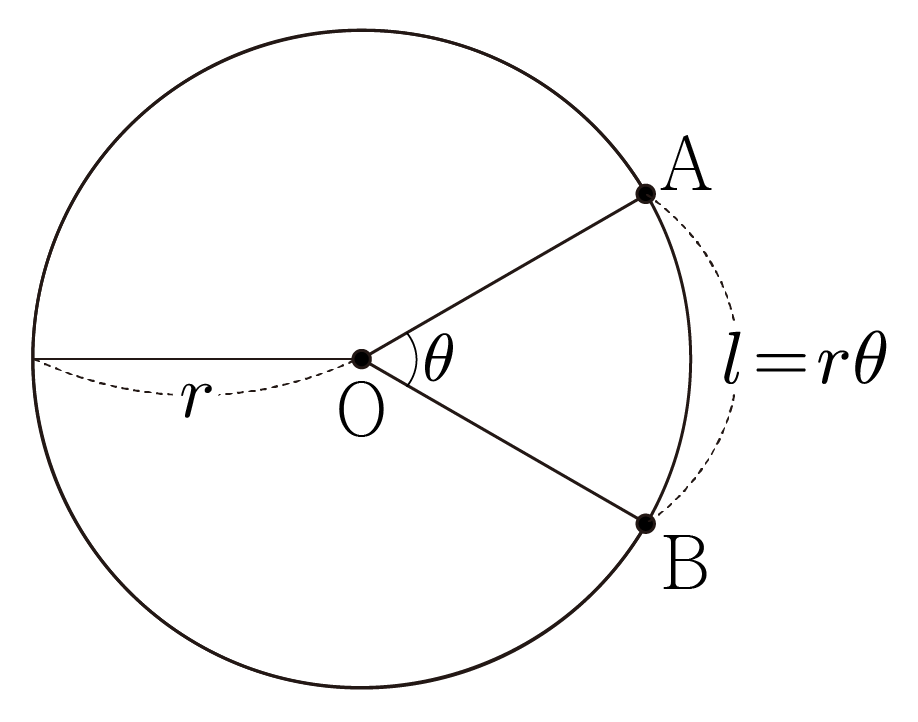
아래 그림과 같이 원의 중심을 O, 호 AB의 길이를 l, ∠AOB=θ(rad), 원의 반지름을 r이라 하면, l=rθ이다.
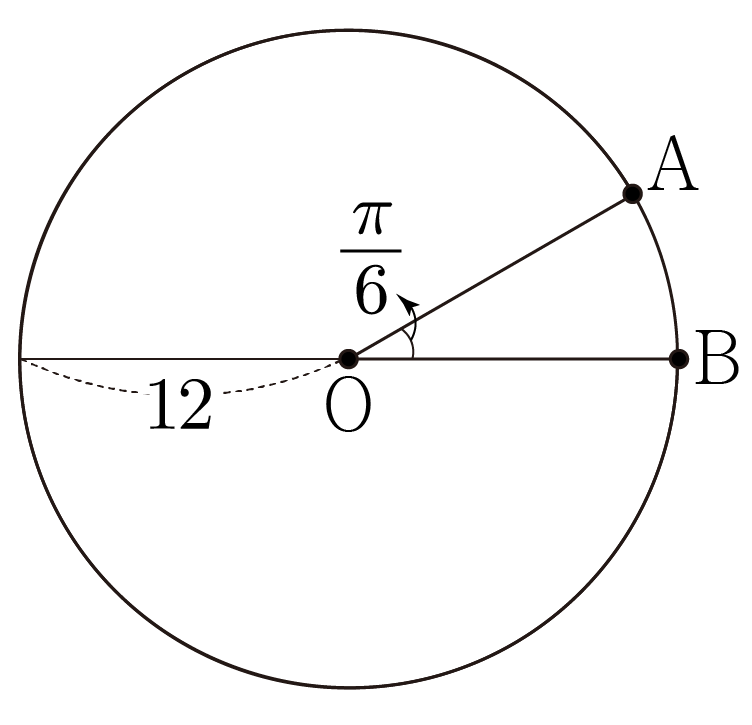
그림과 같이 중심이 O이고 반지름이 12인 원 위에 두 점 A,B가 있다.
∠AOB=6π일 때, 호 AB의 길이를 구해보자.
호 AB의 길이를 l, ∠AOB=θ(rad), 원의 반지름을 r이라 하면, l=rθ이므로 l=12×6π=2π이다.
정답: $3$
라디안=도$\times\frac{\pi\thinspace\mathrm{rad}}{180^\circ}$이므로
45∘×180∘πrad=4πrad=4π(rad은 생략 가능)이다.
따라서 정답은 3번이다.
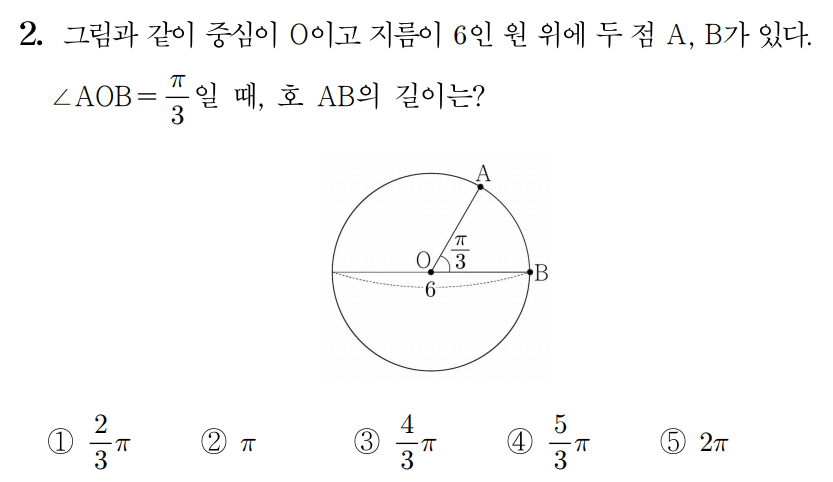
정답: $2$
지름은 반지름의 2배와 같으므로 반지름은 지름의 21배이다.
그러므로 원의 반지름은 6×21=3이다.
호 AB의 길이를 l, ∠AOB=θ(rad), 원의 반지름을 r이라 하면, l=rθ이므로
l=3×3π=π이다.
따라서 정답은 2번이다.