한 각이 직각인 삼각형이다.
변은 도형의 외곽을 이루는 선을 의미하며, 점 A, B를 잇는 변은 AB로 표기한다.
AB의 길이가 l일 때, AB=l과 같이 표기한다.
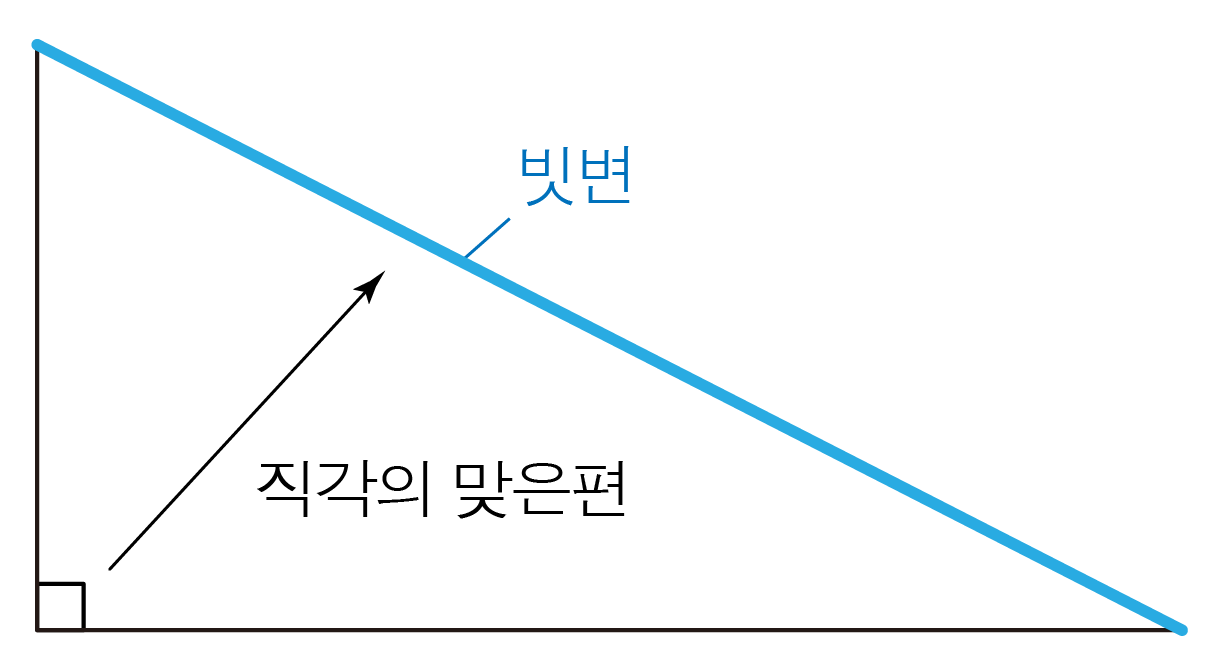
직각 삼각형의 변은 빗변, 대변, 인접변의 3가지가 존재한다.
- 빗변: 직각 삼각형에서 가장 긴 변으로 직각의 맞은편에 있는 변이다.
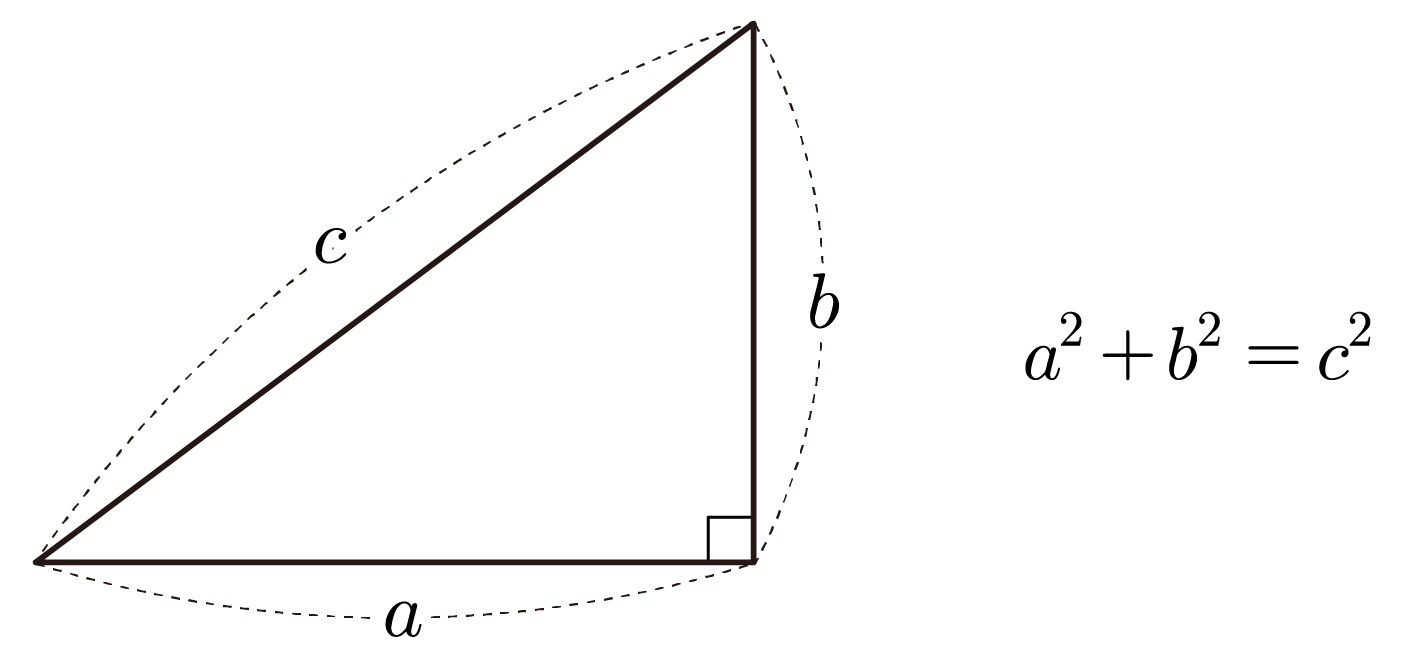
직각 삼각형에서 빗변의 길이를 c, 나머지 두 변의 길이를 각각 a, b라 할 때, a2+b2=c2이다.
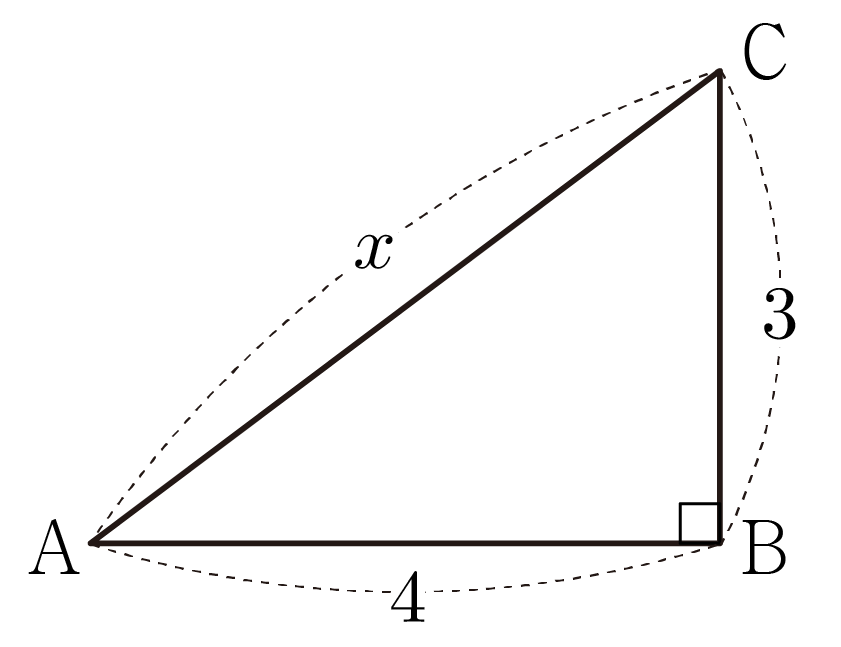
그림과 같이 AB=4, BC=3, AC=x인 직각 삼각형 ABC가 있을 때 x의 값을 구해보자.
AC는 빗변에 해당하므로 피타고라스 정리에 의해 42+32=x2,
16+9=x2,
25=x2,
52=x2,
x=5이다.
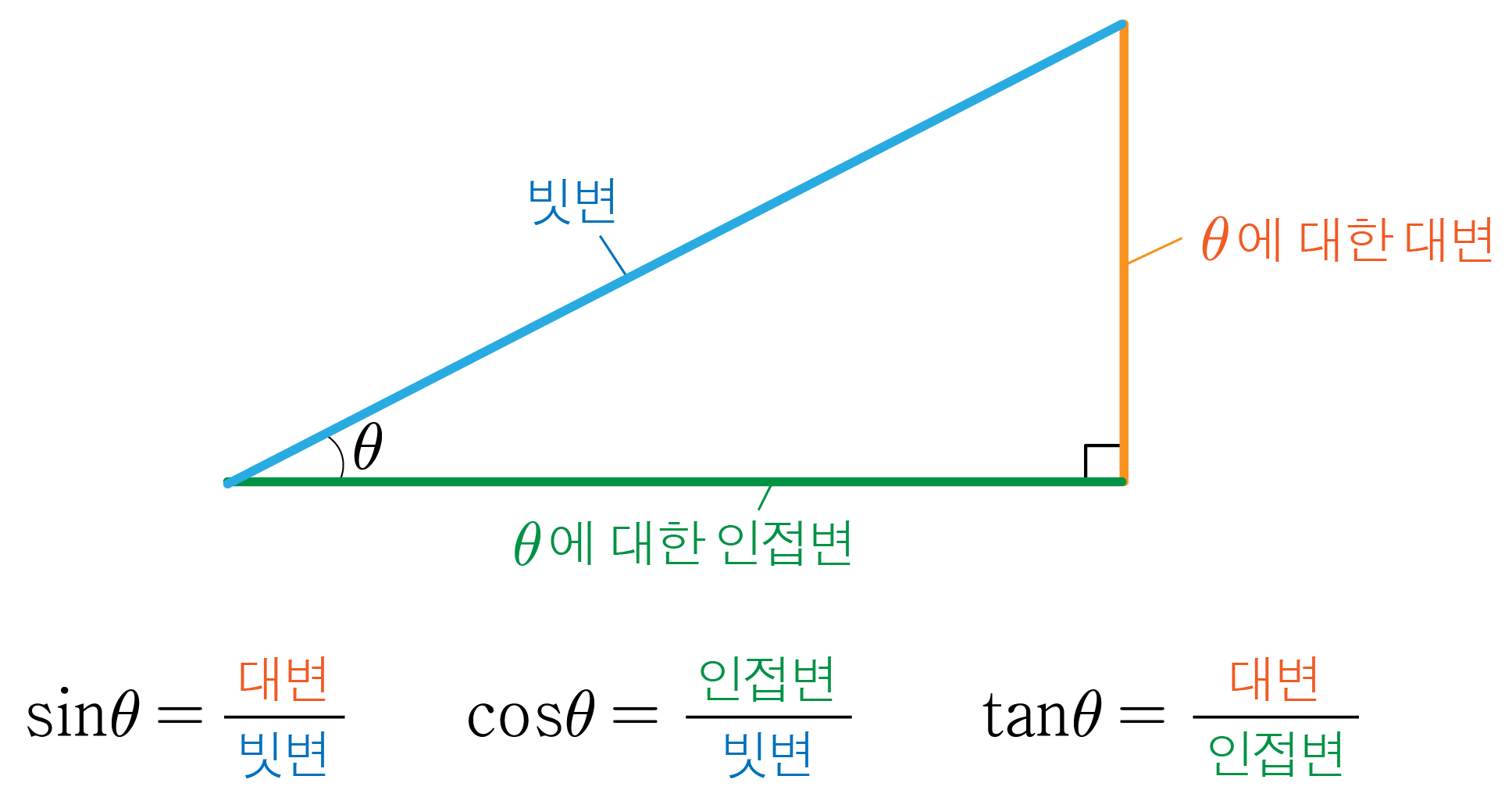
직각 삼각형에서 각도와 변의 길이 사이의 관계를 나타낸 비율이다. sin(사인), cos(코사인), tan(탄젠트)를 주로 활용한다.
특정 각도 θ에 대하여 sinθ=빗변대변, cosθ=빗변인접변, tanθ=인접변대변이다.
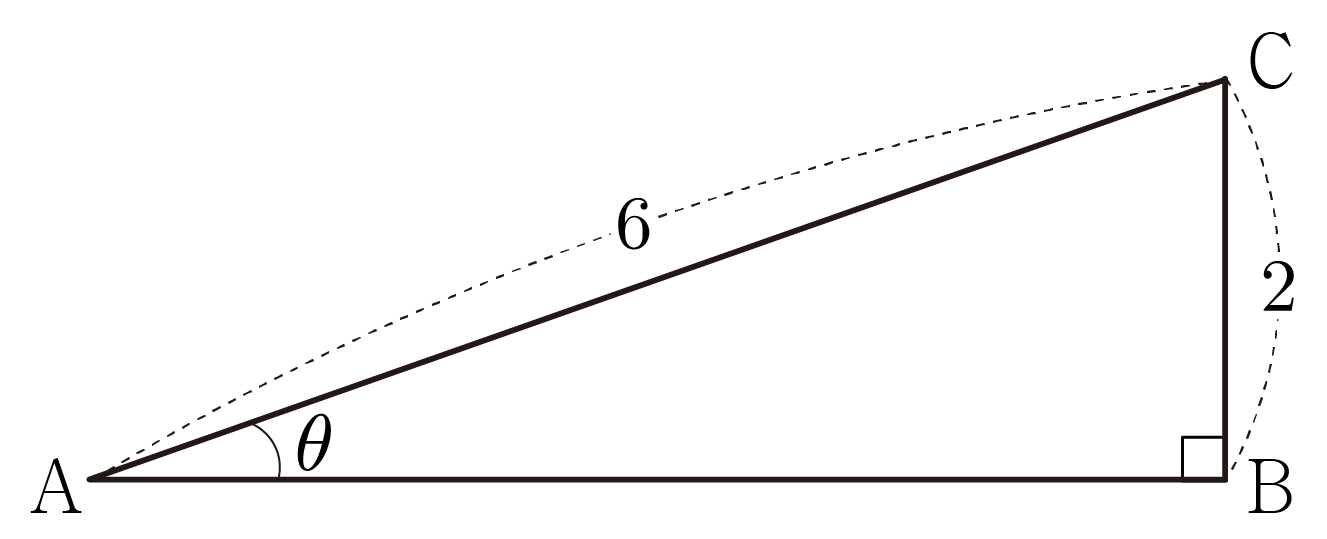
그림과 같이 AC=6, BC=2, ∠BAC=θ인 직각 삼각형 ABC가 있을 때 sinθ의 값을 구해보자.
빗변은 직각 삼각형에서 가장 긴 변으로 직각의 맞은편에 있는 변이고,
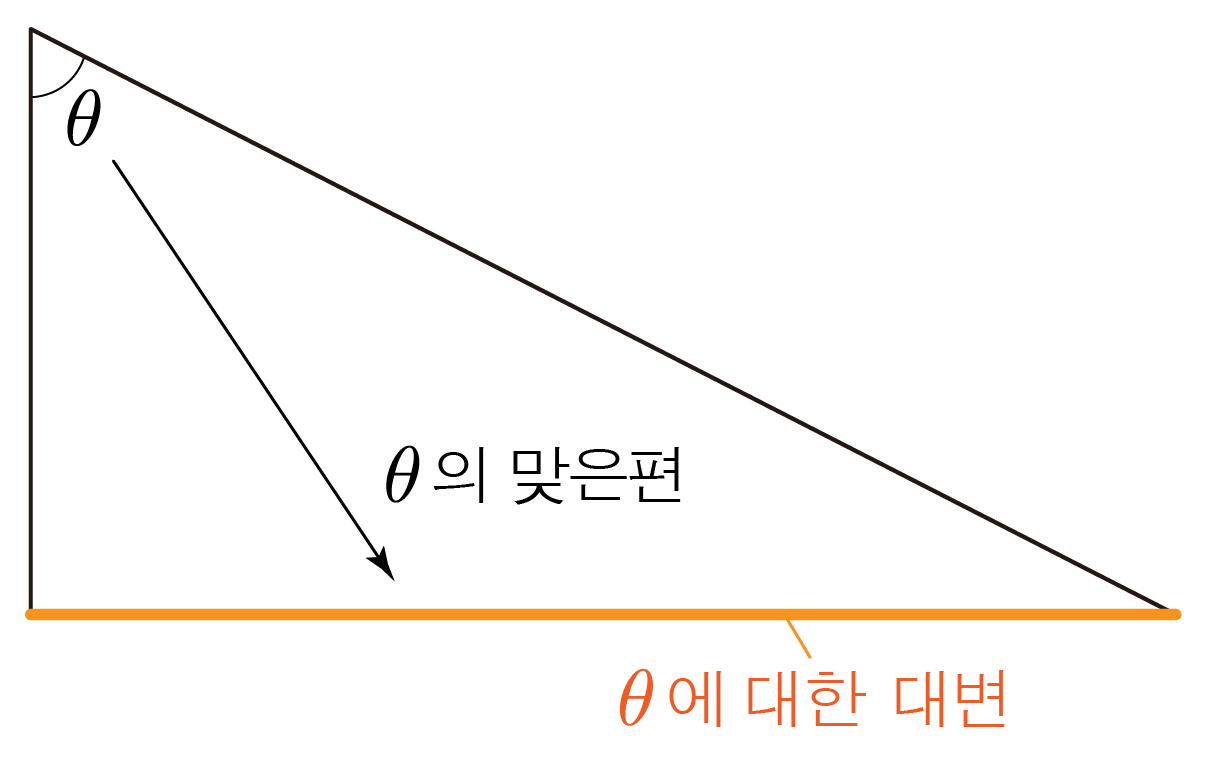
대변은 특정 각도의 맞은편에 있는 변이므로 AC가 빗변, θ에 대하여 BC가 대변에 해당한다.
따라서 sinθ=빗변대변=62=31이다.
θ가 30∘, 45∘, 60∘일 때의 각도이다. 특수각일 때 삼각비는 아래 표와 같다.
| $\theta$ |
$\sin\theta$ |
$\cos\theta$ |
$\tan\theta$ |
| $30^\circ$ |
$\frac{1}{2}$ |
$\frac{\sqrt{3}}{2}$ |
$\frac{1}{\sqrt{3}}$ |
| $45^\circ$ |
$\frac{\sqrt{2}}{2}$ |
$\frac{\sqrt{2}}{2}$ |
$1$ |
| $60^\circ$ |
$\frac{\sqrt{3}}{2}$ |
$\frac{1}{2}$ |
$\sqrt{3}$ |
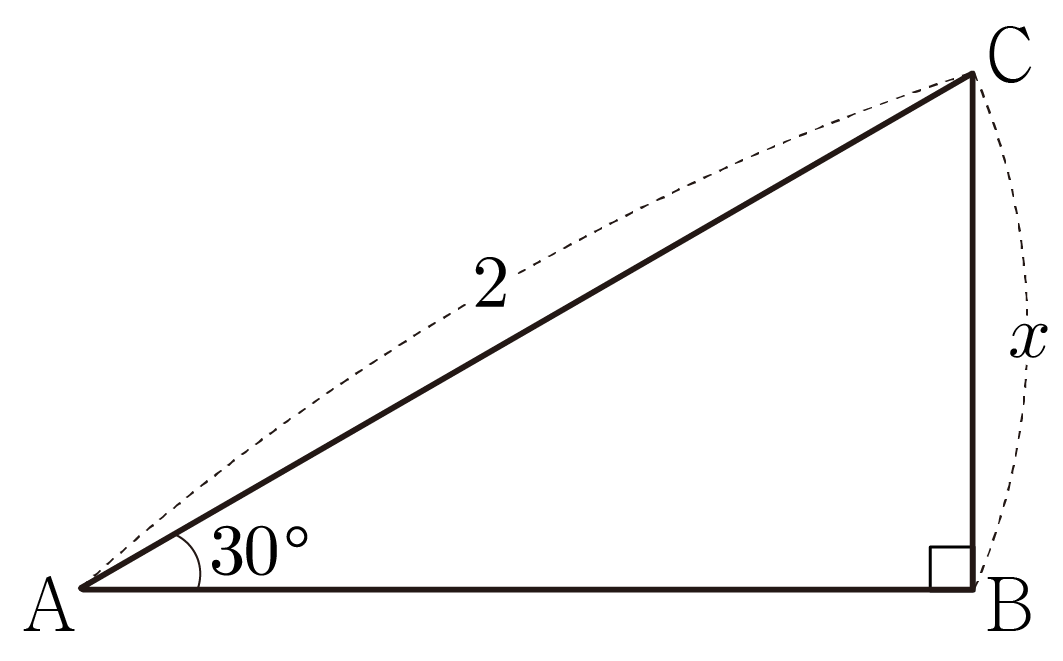
그림과 같이 AC=2, BC=x, ∠BAC=30∘인 직각 삼각형 ABC가 있을 때 x의 값을 구해보자.
빗변은 직각 삼각형에서 가장 긴 변으로 직각의 맞은편에 있는 변이고,
대변은 특정 각도의 맞은편에 있는 변이므로 AC가 빗변, ∠BAC에 대하여 BC가 대변에 해당한다.
따라서 sin30∘=빗변대변=2x인데, 특수각 30∘에서 sin30∘=21이므로
sin30∘=2x=21,
x=1이다.
정답: $2$
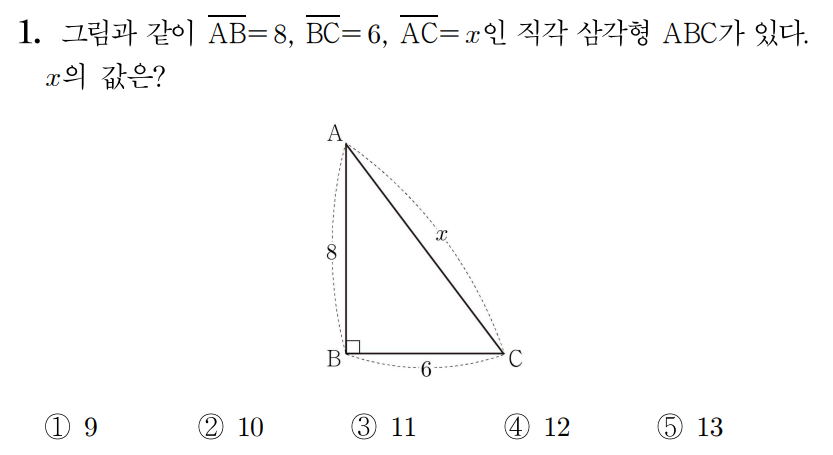
AC는 빗변에 해당하므로 피타고라스 정리에 의해 82+62=x2,
64+36=x2,
100=x2,
102=x2,
x=10이다.
따라서 정답은 2번이다.
정답: $1$
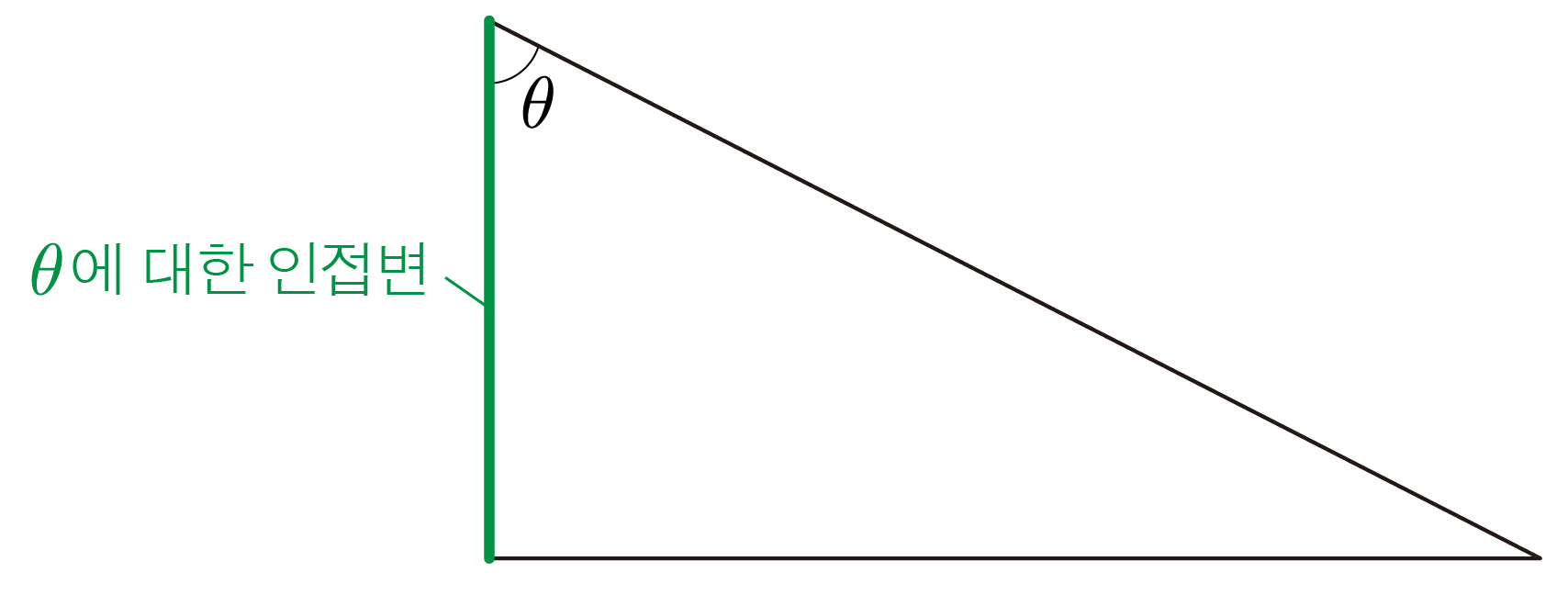
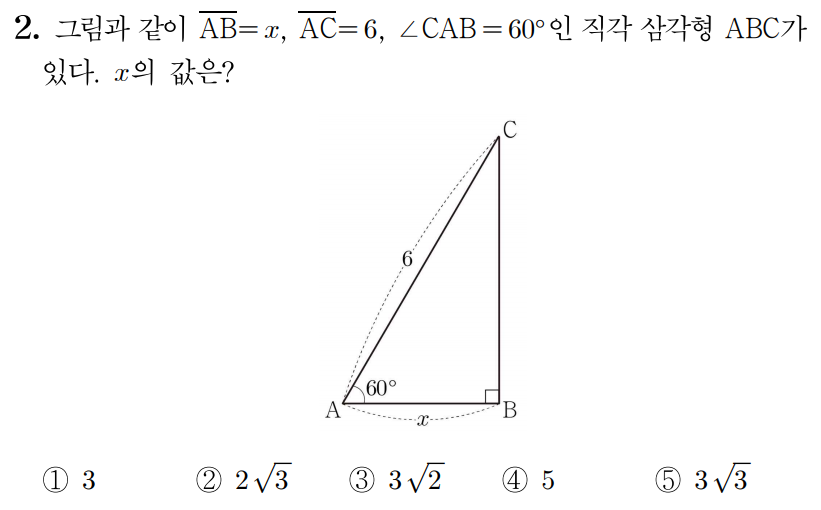
빗변은 직각 삼각형에서 가장 긴 변으로 직각의 맞은편에 있는 변이고, 대변은 특정 각도의 맞은편에 있는 변이며, 빗변과 대변이 아닌 변은 인접변이다.
그러므로 AC가 빗변, ∠CAB에 대하여 BC가 대변, AB가 인접변에 해당한다.
cos60∘=빗변인접변=6x인데, 특수각 60∘에서 cos60∘=21이므로
cos60∘=6x=21,
x=3이다.
따라서 정답은 1번이다.