¶ 지식 정보
| 해당 지식 | |
|---|---|
|
|
| 하위 지식 | 상위 지식 |
|
|
¶ 넓이
평면에서 도형이 차지하는 크기이다.
¶ 표면적
물체의 겉면의 전체 넓이이다.
¶ 부피
공간에서 도형이 차지하는 크기이다.
¶ 원의 넓이
원의 넓이를 , 반지름을 이라 할 때, 이다.
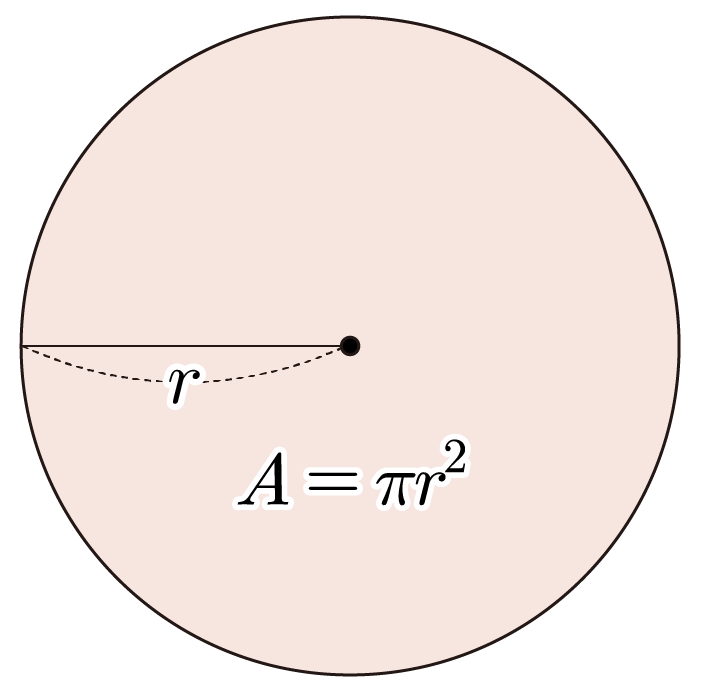
¶ 원의 넓이 예시
아래 그림과 같이 반지름이 인 원의 넓이를 구해보자.
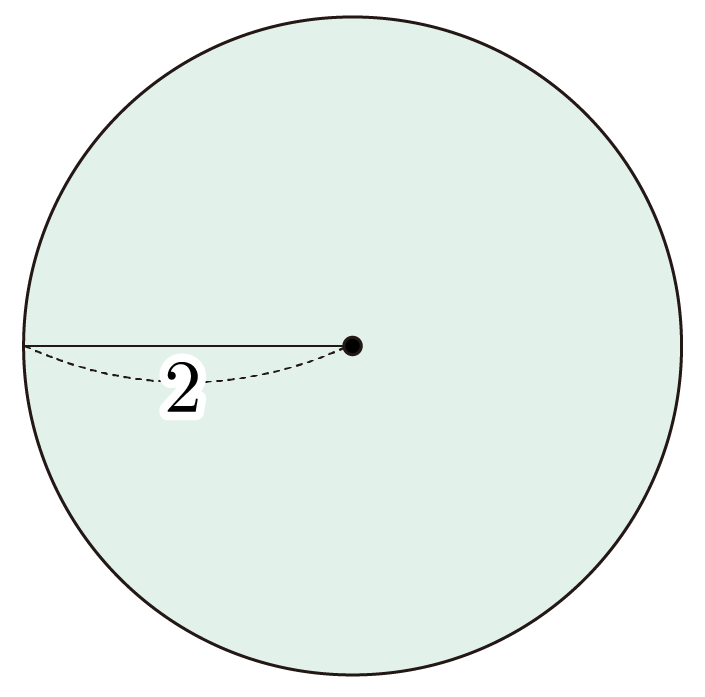
원의 넓이를 , 반지름을 이라 할 때, 이므로
이다.
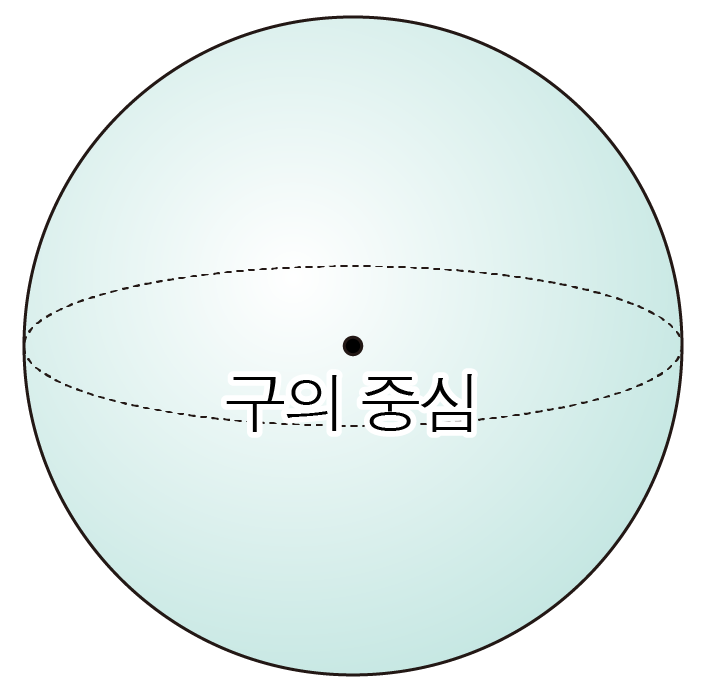
¶ 구
공간에서 가운데 점을 중심으로 같은 거리만큼 떨어진 점들로 이루어진 도형이다.
¶ 구의 표면적
구의 표면적을 , 반지름을 이라 할 때, 이다.
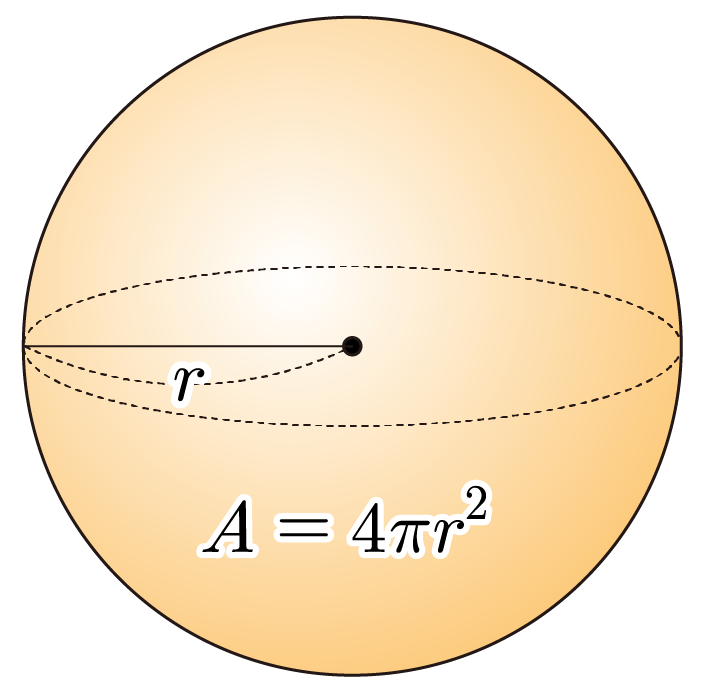
¶ 구의 표면적 예시
아래 그림과 같이 반지름이 인 구의 표면적을 구해보자.
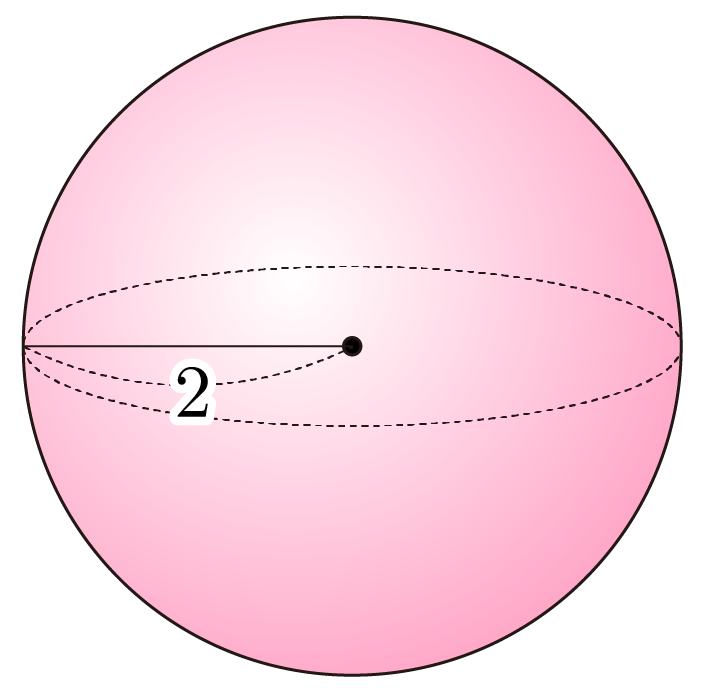
구의 표면적을 , 반지름을 이라 할 때, 이므로
이다.
¶ 구의 부피
구의 부피를 , 반지름을 이라 할 때, 이다.
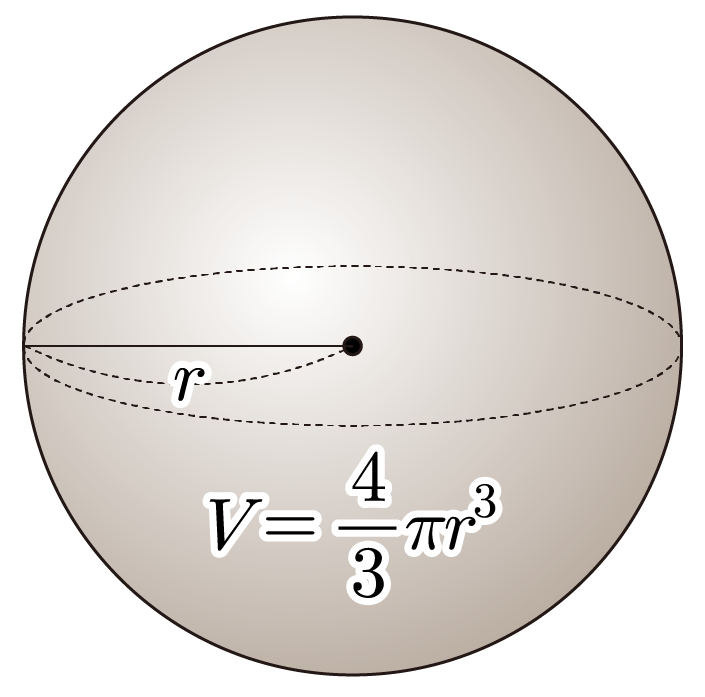
¶ 구의 부피 예시
아래 그림과 같이 반지름이 인 구의 부피를 구해보자.
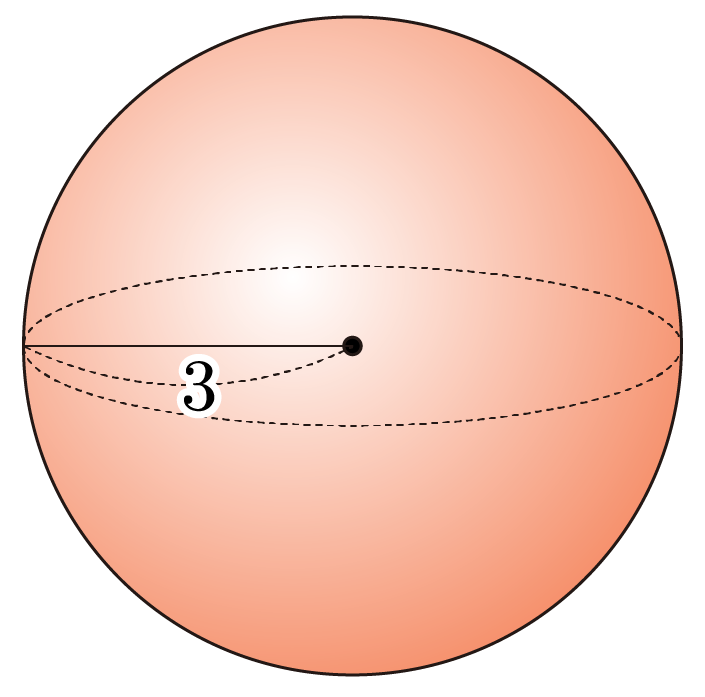
구의 부피를 , 반지름을 이라 할 때, 이므로
이다.
¶ 원기둥
윗면과 아랫면이 동일한 반지름을 가지는 원이고, 그 사이는 펼치면 직사각형이 되는 곡면으로 이루어진 도형이다.
¶ 원기둥의 부피
원기둥의 부피를 , 윗면 또는 아랫면의 반지름을 , 원기둥의 높이를 라 할 때, 이다.
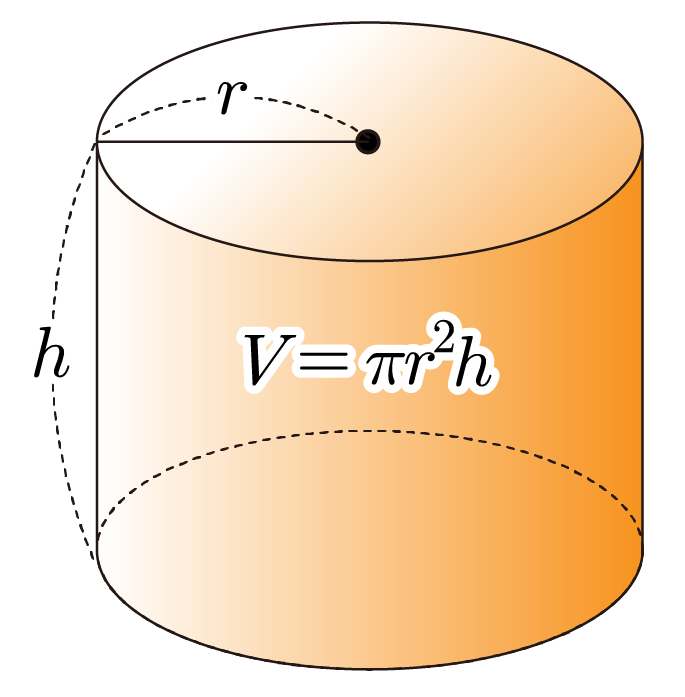
¶ 원기둥의 부피 예시
아래 그림과 같이 윗면의 반지름이 이고, 높이가 인 원기둥의 부피를 구해보자.
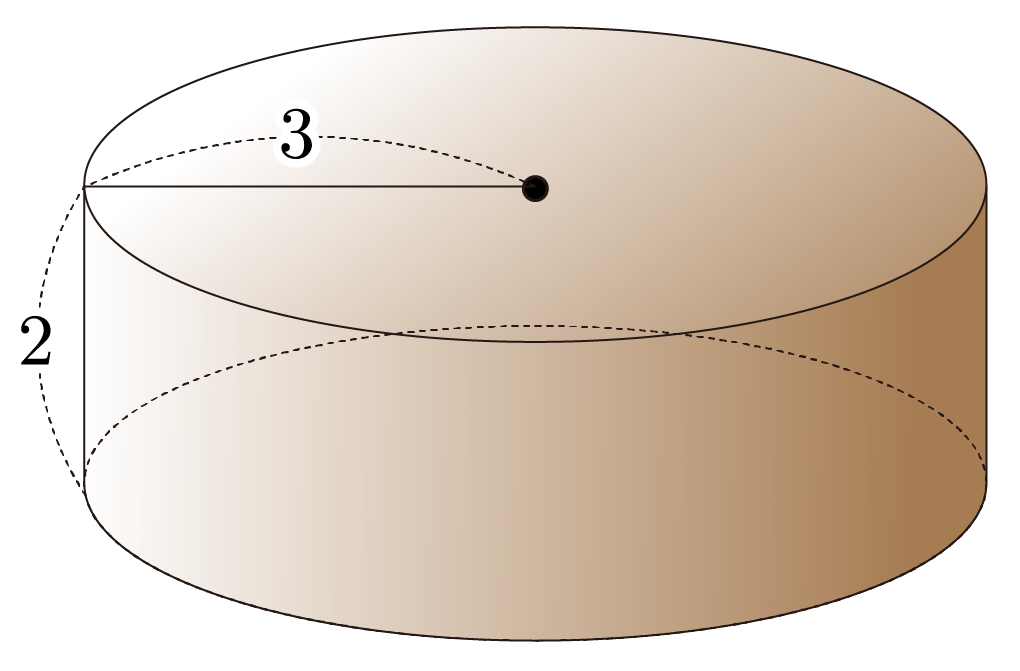
원기둥의 부피를 , 윗면 또는 아랫면의 반지름을 , 원기둥의 높이를 라 할 때, 이므로
이다.
¶ 직육면체
모든 면이 직사각형이고, 개의 면으로 이루어진 도형이다.
¶ 직육면체의 부피
직육면체의 부피를 , 가로를 , 세로를 , 높이를 라 할 때, 이다.
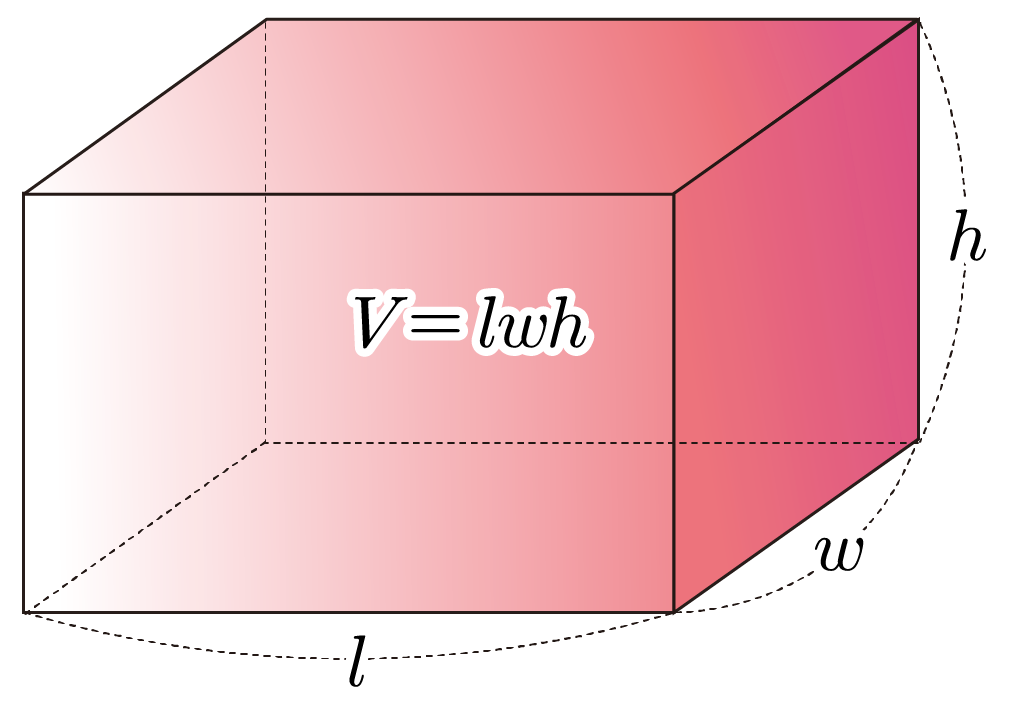
¶ 직육면체의 부피 예시
그림과 같이 가로가 , 세로가 , 높이가 인 직육면체의 부피를 구해보자.
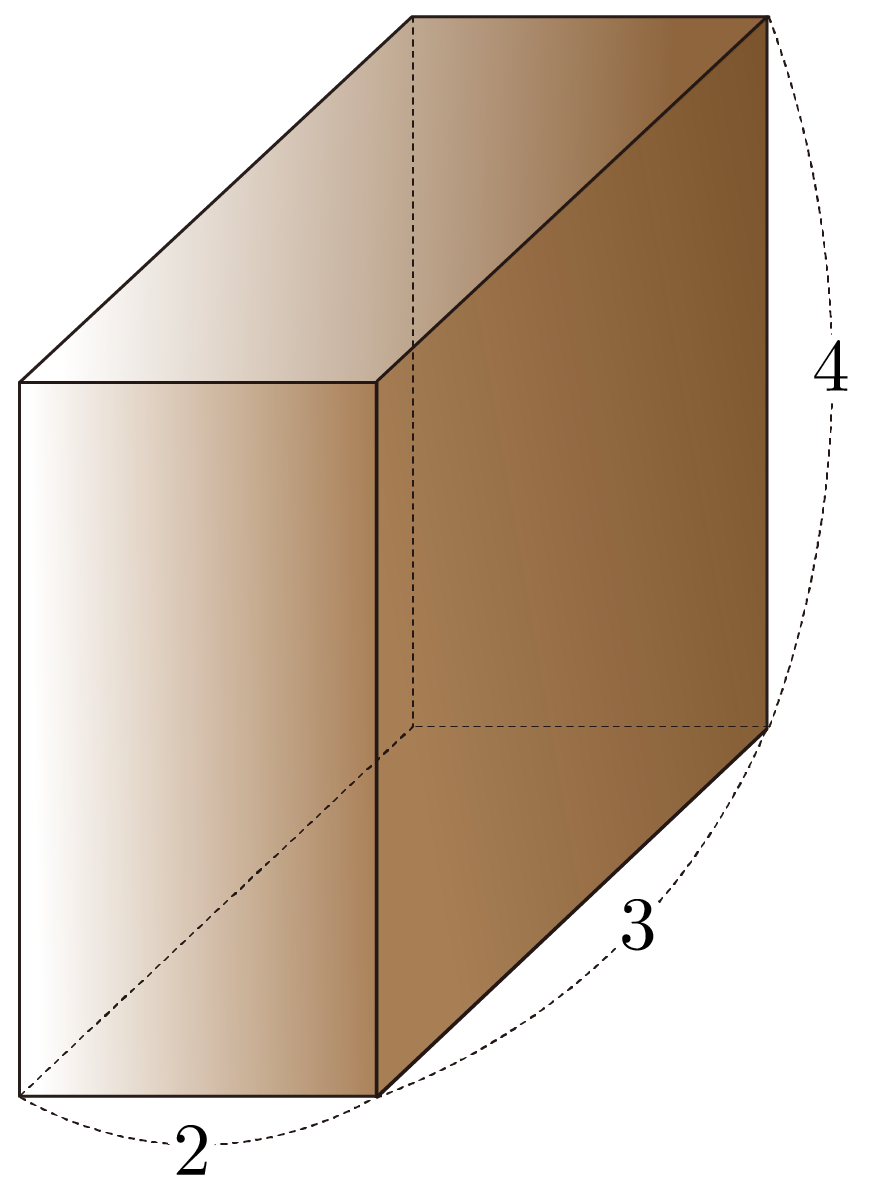
직육면체의 부피를 , 가로를 , 세로를 , 높이를 라 할 때, 이므로
이다.
¶ 적용 문항
¶ 1번 문항
정답: $3$
구의 부피를 , 반지름을 이라 할 때, 이므로
이다.
따라서 정답은 번이다.
¶ 2번 문항
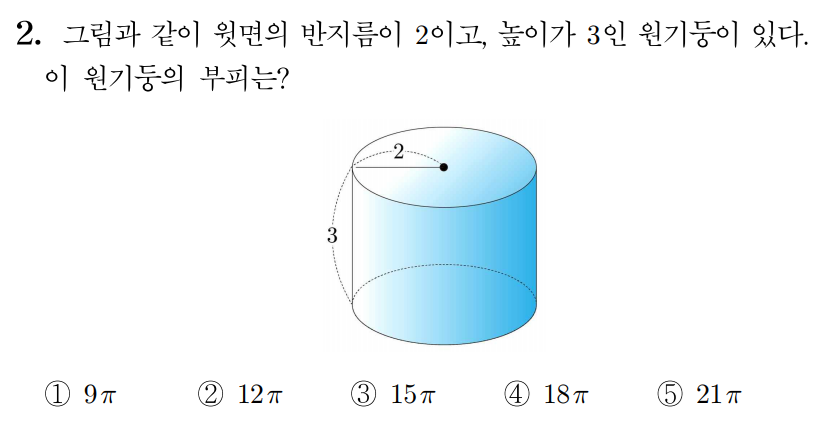
정답: $2$
원기둥의 부피를 , 윗면 또는 아랫면의 반지름을 , 원기둥의 높이를 라 할 때, 이므로
이다.
따라서 정답은 번이다.