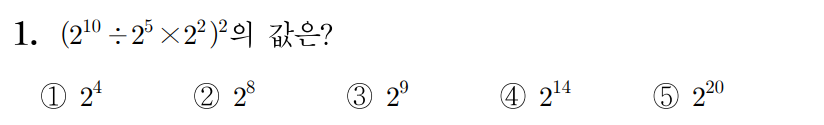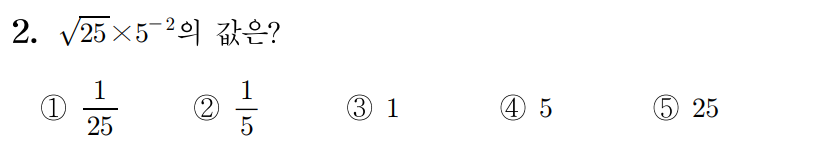곱했을 때 1이 되는 수를 말한다. a의 역수는 a1 (단, a가 0인 경우는 제외)이다.
3의 역수는 31, x의 역수는 x1이다.
어떤 수를 반복적으로 곱할 때 간단히 표현하는 방법이다.
an은 1에 a를 n번 곱하는 것을 의미한다.
여기서 a는 밑, n은 지수라 하며, an은 ‘a의 n제곱’ 또는 ‘a의 n승’이라 읽는다.
23은 1에 2를 3번 곱하는 것을 의미하므로, 23=1×2×2×2=8이다.
23에서 2는 밑, 3은 지수라 하며, 23은 ‘2의 3제곱’ 또는 ‘2의 3승’이라 읽는다.
- 같은 밑을 가진 거듭제곱의 곱은 지수를 더해서 계산한다.
am×an=am+n
예시: $2^{9}\times 2^{3}=2^{9+3}=2^{12}$
- 같은 밑을 가진 거듭제곱의 나눗셈은 지수를 빼서 계산한다.
am÷an=am−n
예시: $2^{9}\div 2^{3}=2^{9-3}=2^{6}$
- 거듭제곱의 거듭제곱은 지수를 곱해서 계산한다.
(am)n=am×n
예시: $(2^{9})^{3}=2^{9\times 3}=2^{27}$
- 지수가 0일 때는 밑과 관계없이 항상 1이다. (단, 밑이 0인 경우는 제외)
a0=1
예시: $2^{0}=1,\ 5^{0}=1$
- 음수인 지수는 밑을 역수로 바꾸고, 지수를 양수로 바꾼 것과 같다.
a−n=(a1)n=an1
예시: $2^{-3}=\left(\frac{1}{2}\right)^{3}=\frac{1}{2^{3}}$
지수가 21인 수로, 동일한 값끼리 곱했을 때 밑이 되는 수이다.
루트는 기호로 2로 나타내며, a는 ‘루트 a’라 읽는다.
a×a=a21×a21=a21+21=a1=1×a=a
4를 다르게 표현해보자.
루트는 지수가 21인 수로 4=421이다.
4=2×2=22이므로
421=(22)21이다. 이때 (am)n=am×n이므로
(22)21=22×21=21=1×2=2이다.
정답: $4$
같은 밑을 가진 거듭제곱의 나눗셈은 지수를 빼서 계산하므로
(210÷25×22)2=(210−5×22)2=(25×22)2이다.
같은 밑을 가진 거듭제곱의 곱은 지수를 더해서 계산하므로
(25×22)2=(25+2)2=(27)2이다.
거듭제곱의 거듭제곱은 지수를 곱해서 계산하므로
(27)2=27×2=214이다.
따라서 정답은 4번이다.
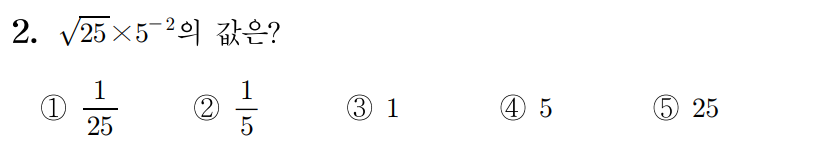
정답: $2$
루트는 지수가 21인 수로 25=2521이다.
여기서 25=5×5=52이므로 2521=(52)21이다.
이때 (am)n=am×n이므로
(52)21=52×21=51이다.
이를 통해 25×5−2=51×5−2임을 알 수 있는데, 같은 밑을 가진 거듭제곱의 곱은 지수를 더해서 계산하므로 51×5−2=51+(−2)=5−1이다.
음수인 지수는 밑을 역수로 바꾸고, 지수를 양수로 바꾼 것과 같으므로
5−1=511=1×51=51이다.
따라서 정답은 2번이다.