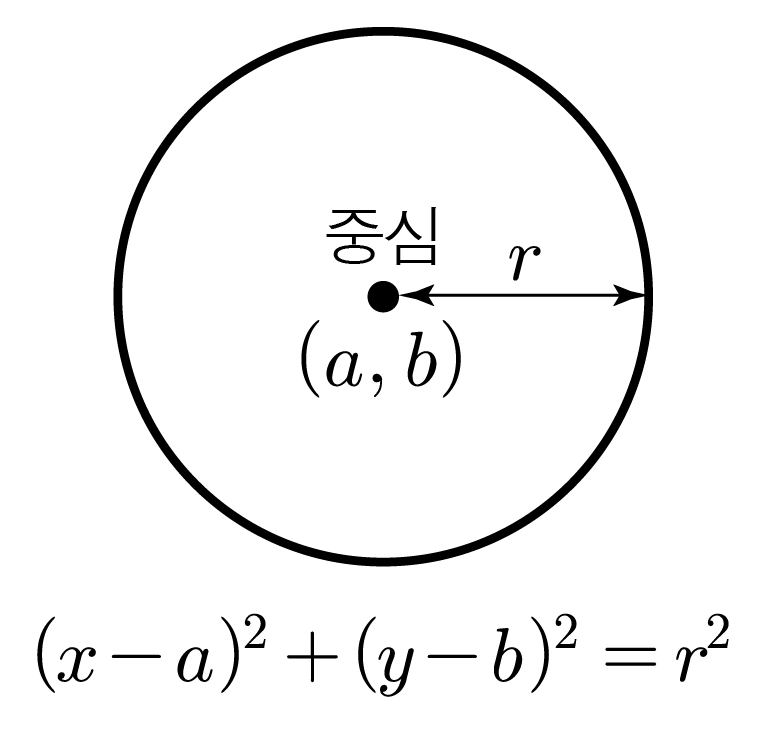
좌표 평면에서 중심의 좌표가 (a,b)이고 반지름이 r인 원의 방정식은 (x−a)2+(y−b)2=r2이다.
예시 1:
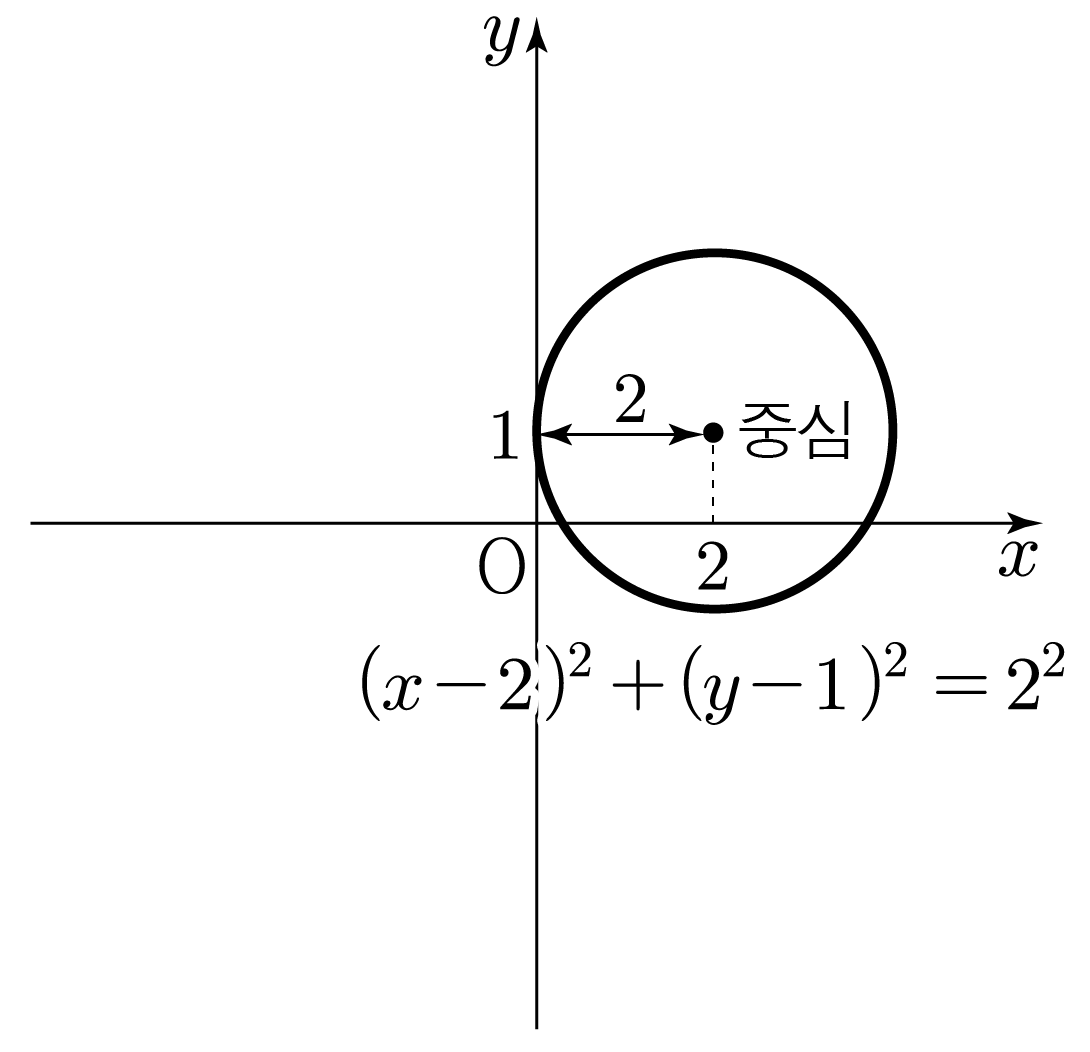
원 (x−2)2+(y−1)2=4를 그려보자.
(x−2)2+(y−1)2=4=22이므로
(x−a)2+(y−b)2=r2에서 a=2,b=1,r=2에 해당한다.
따라서 (x−2)2+(y−1)2=4는 중심의 좌표가 (2,1)이고 반지름이 2인 원이므로 그리면 아래와 같다.
예시 2:
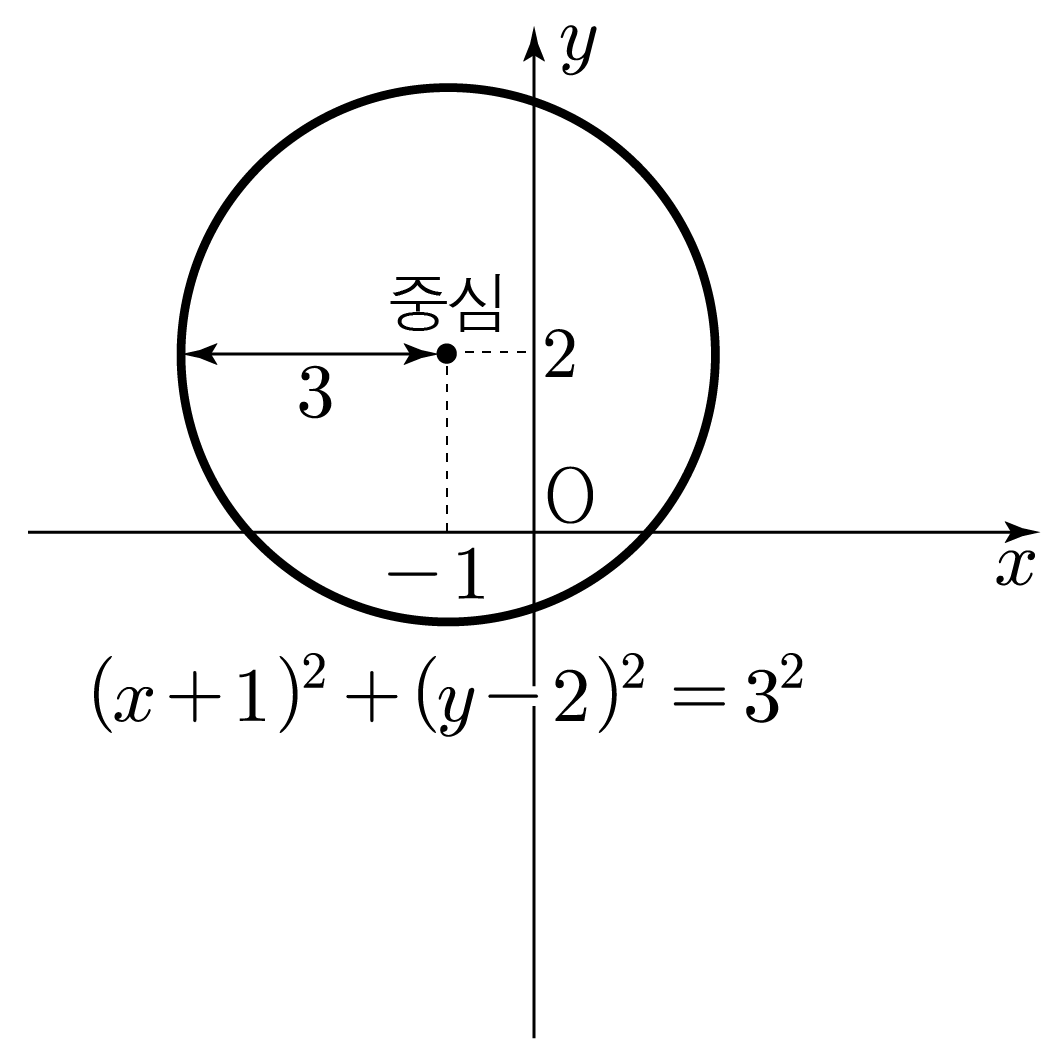
원 (x+1)2+(y−2)2=9를 그려보자.
(x+1)2+(y−2)2=9=32이므로
(x−a)2+(y−b)2=r2에서 a=−1,b=2,r=3에 해당한다.
따라서 (x+1)2+(y−2)2=9는 중심의 좌표가 (−1,2)이고 반지름이 3인 원이므로 그리면 아래와 같다.
정답: $3$
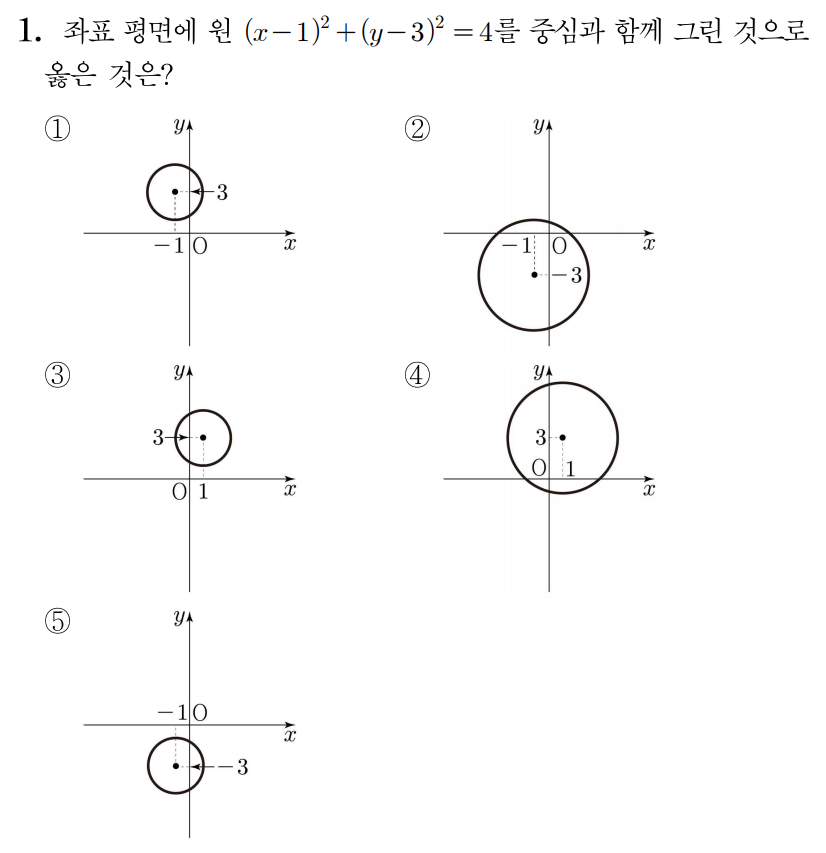
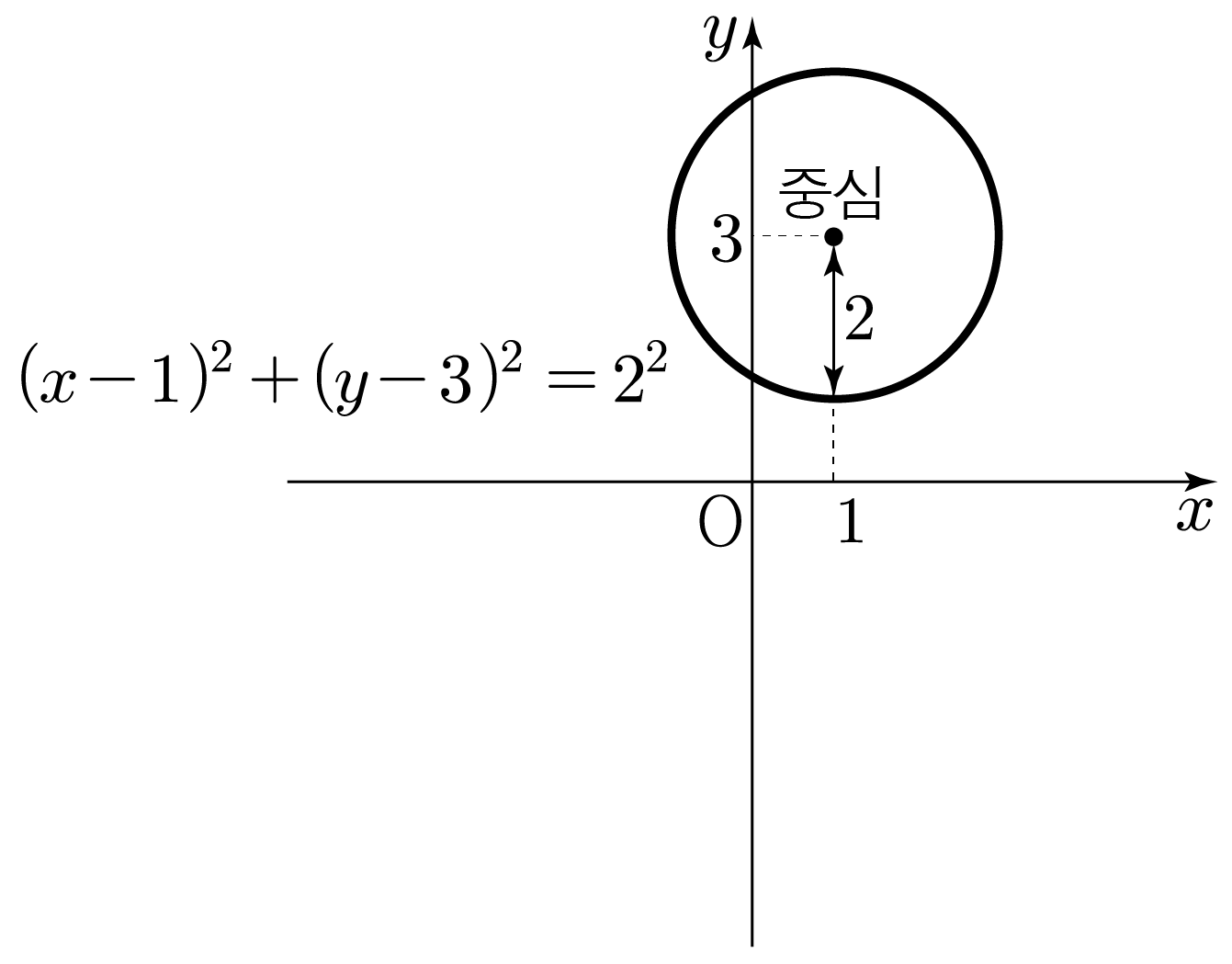
(x−1)2+(y−3)2=4=22이므로
(x−a)2+(y−b)2=r2에서 a=1,b=3,r=2에 해당한다.
그러므로 (x−1)2+(y−3)2=4는 중심의 좌표가 (1,3)이고 반지름이 2인 원이므로 그리면 아래와 같다.
따라서 정답은 3번이다.
정답: $1$
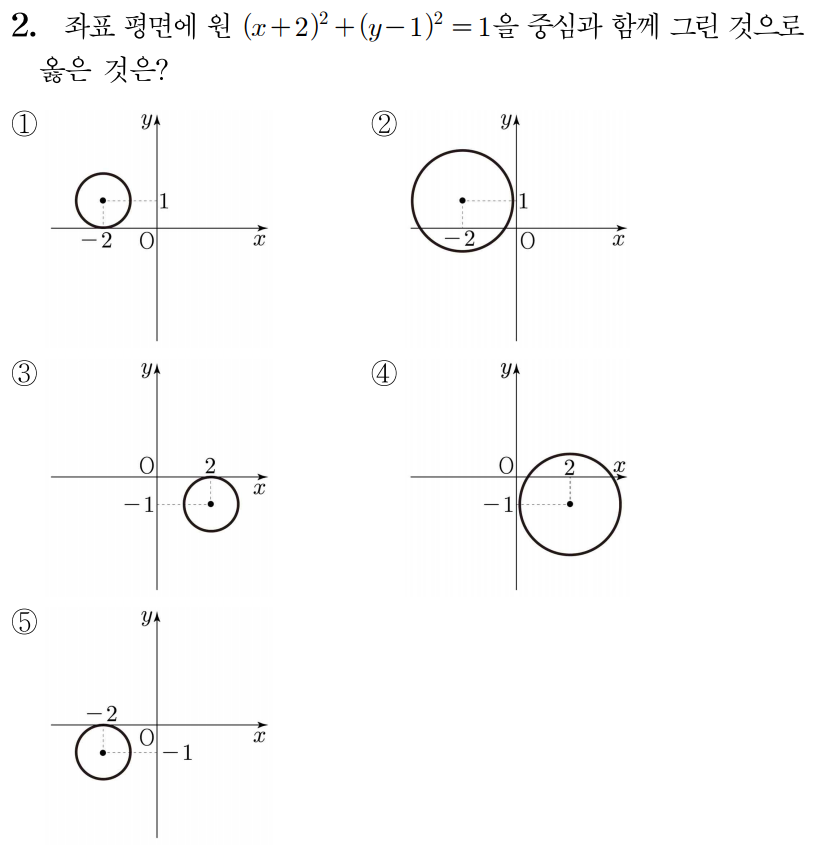
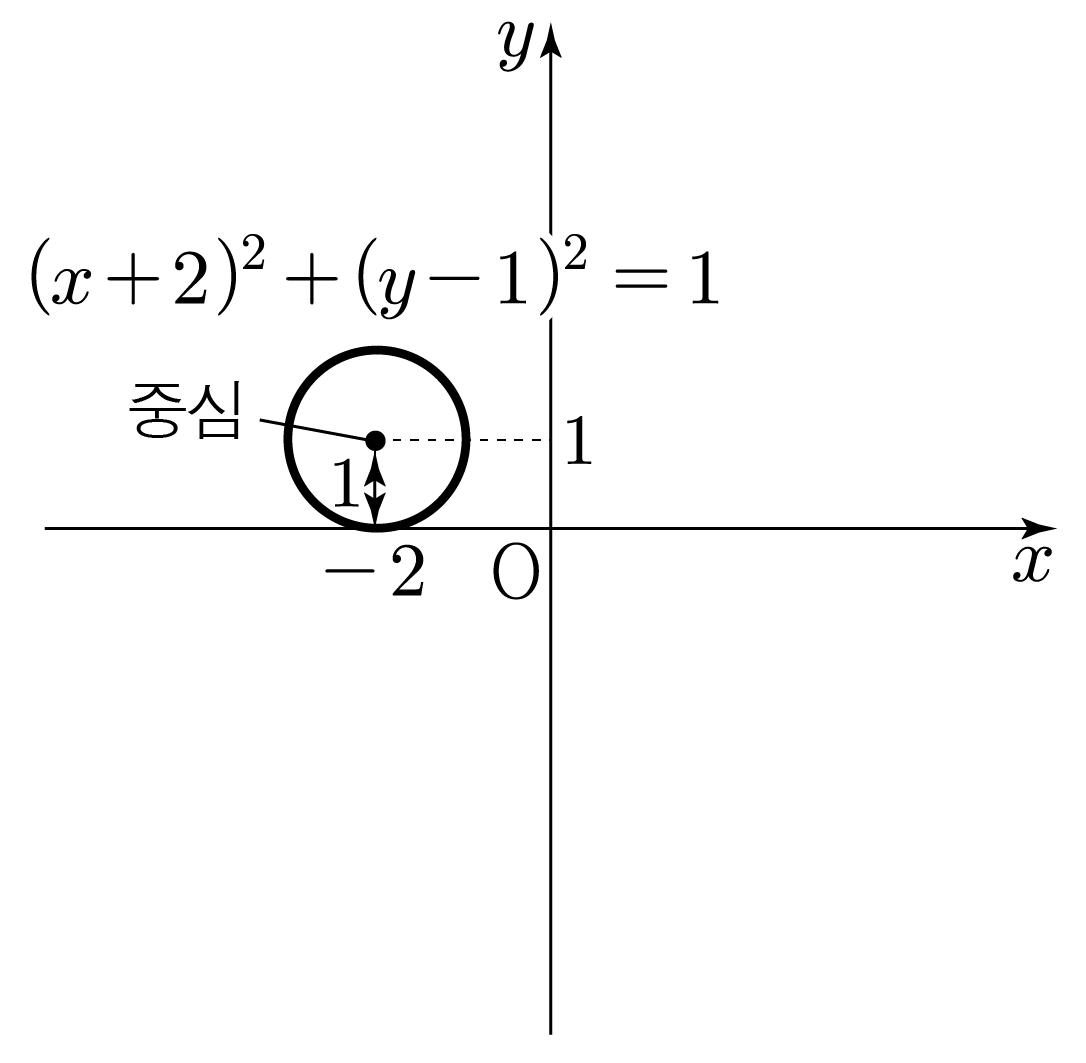
(x+2)2+(y−1)2=1=12이므로
(x−a)2+(y−b)2=r2에서 a=−2,b=1,r=1에 해당한다.
그러므로 (x+2)2+(y−1)2=1은 중심의 좌표가 (−2,1)이고 반지름이 1인 원이므로 그리면 아래와 같다.
따라서 정답은 1번이다.
