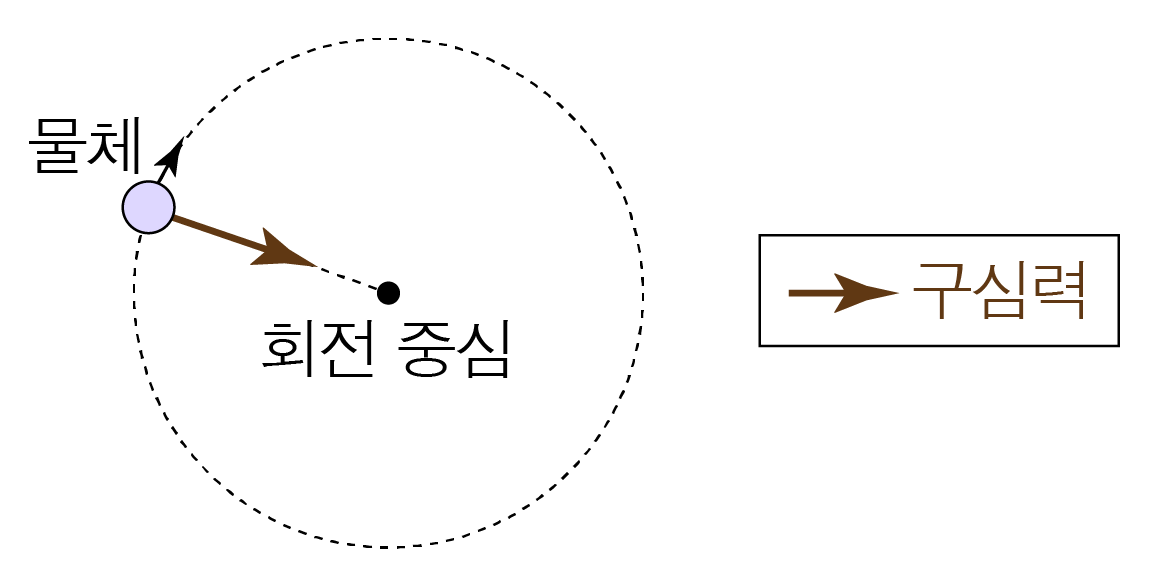
원 궤도를 따라 일정한 속력으로 회전하는 운동이다.
원운동에서 주기는 한 바퀴 회전하는 데 걸리는 시간을 의미하고,
진동수는 단위 시간 동안의 회전 수이다.
주기의 기본 단위는 s(초)이고, 기호로는 T로 나타낸다.
진동수의 기본 단위는 s−1=Hz이고, Hz는 ‘헤르츠’로 읽는다. 진동수는 기호 f로 나타낸다.
진동수와 주기는 서로 역수 관계이기 때문에 f=T1 또는 T=f1이다.
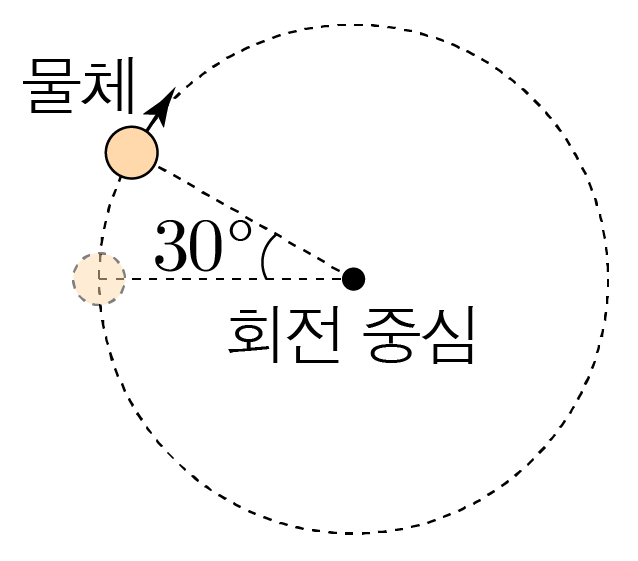
그림은 등속 원운동하는 물체가 1초 동안 30∘ 만큼 회전한 것을 나타낸 것이다.
이때 원운동의 주기와 진동수를 구해보자.
-
주기 구하기:
1초 동안 물체는 30∘만큼 회전하므로 물체가 한 바퀴(360∘) 회전하는 데 걸리는 시간은 12초이다.
주기는 한 바퀴 회전하는 데 걸리는 시간을 의미하므로, 원운동의 주기는 12초이다.
-
진동수 구하기:
진동수는 단위 시간 동안의 회전 수이고 30∘는 360∘30∘=121바퀴이므로, 원운동의 진동수는 1s121(바퀴)=121s−1=121Hz이다.
주기는 12초, 진동수는 121Hz로 서로 역수 관계에 있음을 확인할 수 있다.
단위 시간 동안 중심각의 변화이다.
기본 단위는 rad/s이고, 기호로는 ω로 나타낸다. ω는 ‘오메가’로 읽는다.
rad/s에서 rad은 각도를 나타내는 비율이므로 다른 단위와 연산시 사라진다.
등속 원운동하는 물체가 시간 t 동안 각도 θ만큼 회전하면 물체의 각속도의 크기는 tθ이다.
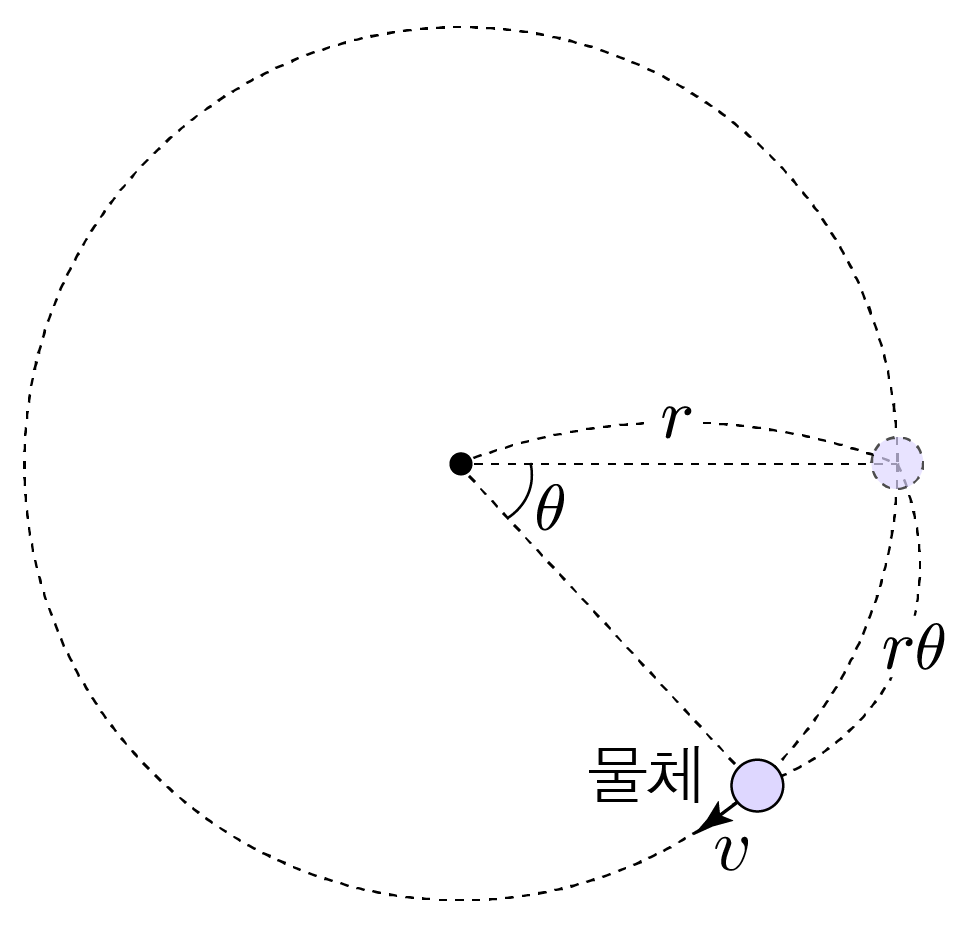
그림과 같이 속력 v로 등속 원운동하는 물체가 시간 t 동안 반지름이 r인 원 궤도를 θ만큼 회전하였다.
t 동안 물체가 이동한 거리는 rθ이므로 v=걸린시간이동거리=trθ=rω이다.
주기 T로 등속 원운동하는 물체는 T(한 바퀴 회전하는 데 걸린 시간) 동안 2π(1바퀴)만큼 회전하므로
ω=T2πrad=T2π=2πf이다.
rad은 각도를 나타내는 비율이므로 생략할 수 있다.
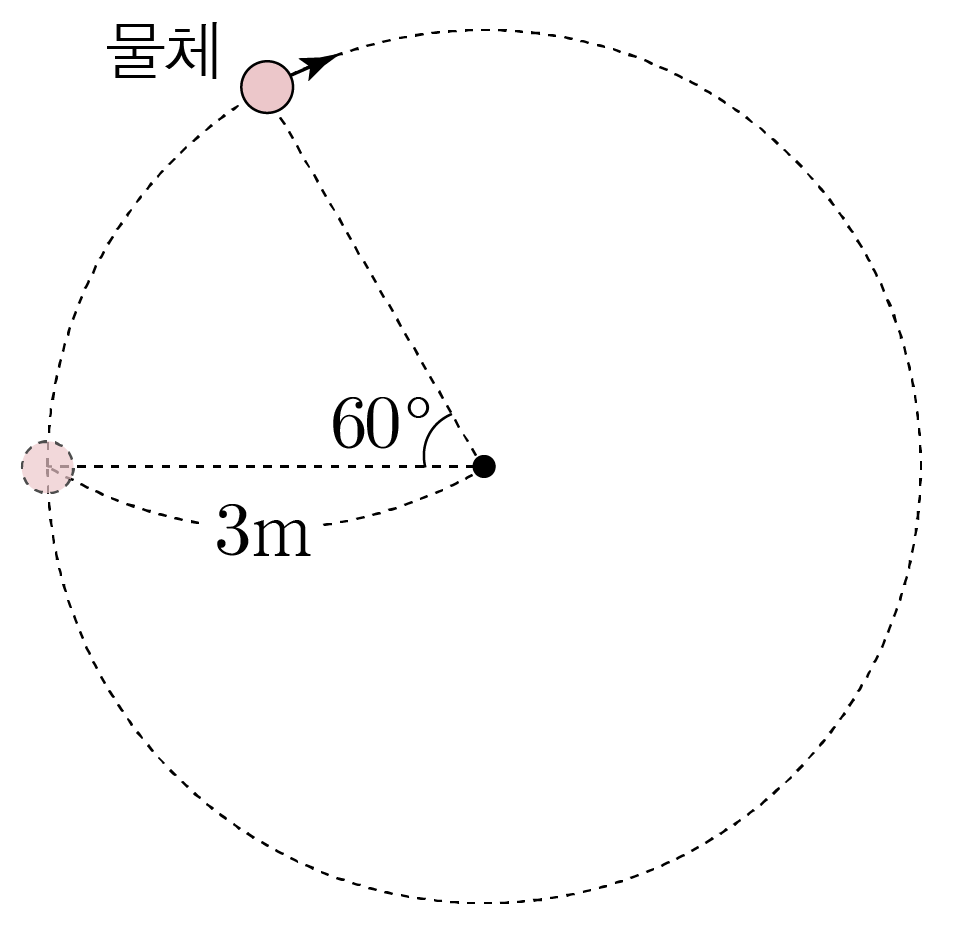
그림은 등속 원운동하는 물체가 1초 동안 60∘만큼 회전한 것을 나타낸 것이다.
원 궤도의 반지름이 3m일 때, 원운동의 주기, 진동수와 물체의 각속도의 크기, 속력을 구해보자.
-
주기 구하기:
1초 동안 물체는 60∘만큼 회전하므로 물체가 한 바퀴(360∘) 회전하는 데 걸리는 시간은 6초이고, 이는 원운동의 주기에 해당한다.
-
진동수 구하기:
진동수는 주기의 역수에 해당하므로 원운동의 진동수는 61s−1=61Hz이다.
-
각속도의 크기 구하기:
원운동 주기를 T, 진동수를 f라 할 때, 물체의 각속도의 크기 ω=T2πrad=2πfrad이므로, ω=6s2πrad=3πrad/s이다.
-
속력 구하기:
회전 반지름을 r이라 할 때, 물체의 속력 v=rω이므로 v=3m×3πrad/s=πm/s이다.
등속 원운동하는 물체의 속력은 일정하지만, 운동 방향이 변하기 때문에 물체에는 알짜힘이 작용한다.
이때 물체의 가속도를 구심 가속도, 물체에 작용하는 알짜힘을 구심력이라 하고,
물체의 가속도와 알짜힘의 방향은 회전 중심 방향이다.
등속 원운동하는 물체의 구심 가속도의 크기 a=rv2이고, 가속도 법칙(F알짜=ma)에 의해
물체에 작용하는 구심력(알짜힘)의 크기를 F구심, 물체의 질량, 회전 반지름, 속력을 각각 m, r, v라 하면,
F구심=m×rv2=rmv2이다.
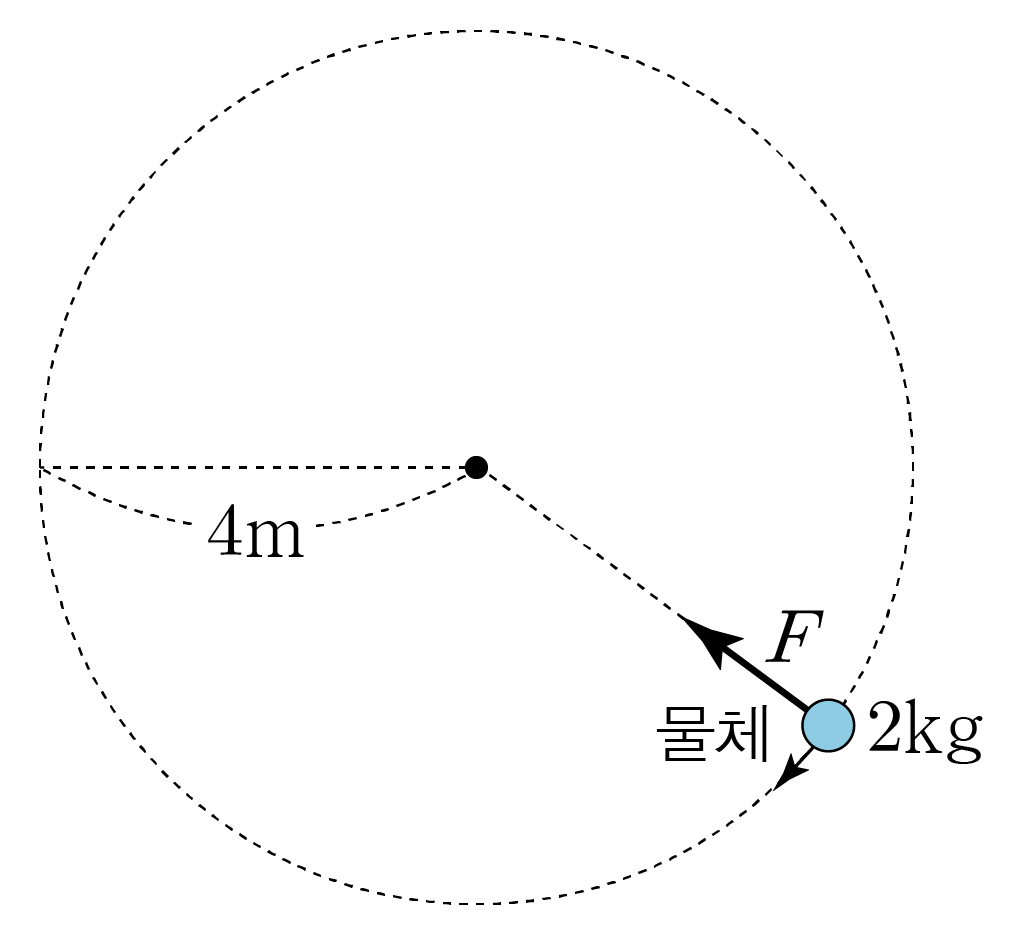
그림은 질량이 2kg인 물체에 크기가 F인 구심력이 작용하여 반지름이 4m인 원 궤도를 따라 등속 원운동하는 것을 나타낸 것이다.
원운동의 주기가 4초일 때, 물체의 각속도의 크기, 속력, 구심 가속도의 크기, 구심력의 크기를 구해보자.
-
각속도의 크기 구하기:
원운동 주기를 T, 진동수를 f라 할 때, 물체의 각속도의 크기 ω=T2πrad=2πfrad이므로,
ω=4s2πrad=2πrad/s=2πs−1이다.
-
속력 구하기:
회전 반지름을 r이라 할 때, 물체의 속력 v=rω이므로
v=4m×2πrad/s=2πm/s이다.
-
구심 가속도의 크기 구하기:
등속 원운동하는 물체의 구심 가속도의 크기 a=rv2이므로
a=4m(2πm/s)2=4m4π2m2/s2=π2m/s2이다.
-
구심력의 크기 구하기:
가속도 법칙(F알짜=ma)에 의해
F=2kg×π2m/s2=2π2kg⋅m/s2=2π2N이다.
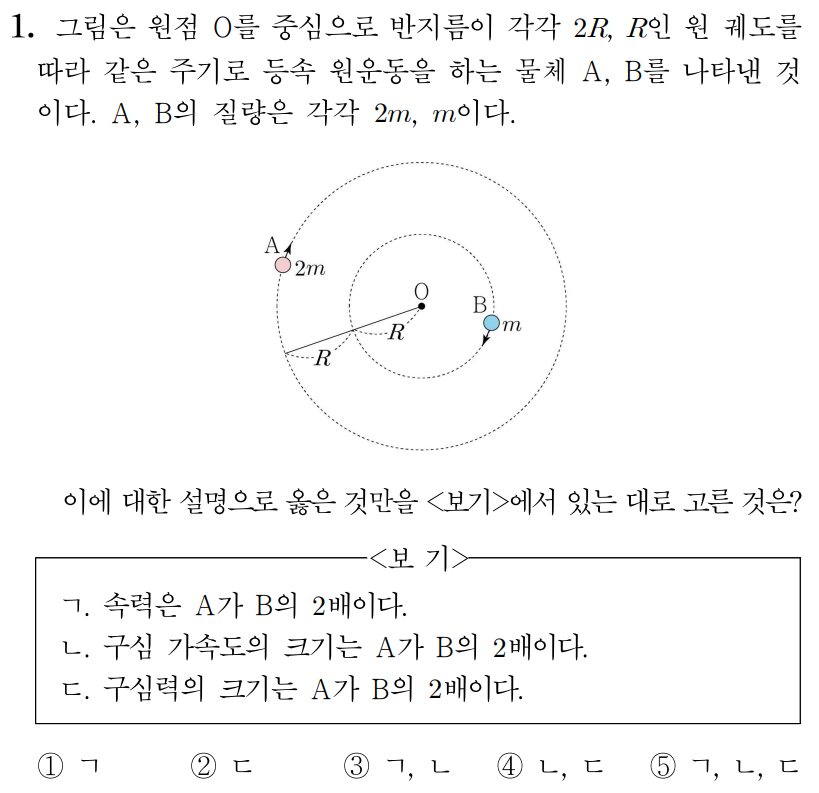
정답: $3$
ㄱ. A와 B의 주기는 같으므로 A와 B의 각속도의 크기는 같다.
A, B의 각속도의 크기를 ω라 하고, A, B의 속력을 각각 vA, vB라 하면,
vA=2Rω, vB=Rω이므로 속력은 A가 B의 2배이다. (O)
ㄴ. A, B의 구심 가속도의 크기를 각각 aA, aB라 하면,
aA=2R(2Rω)2=2R4R2ω2=2Rω2,
aB=R(Rω)2=RR2ω2=Rω2이므로
구심 가속도의 크기는 A가 B의 2배이다. (O)
ㄷ. A, B의 구심력의 크기를 각각 FA, FB라 하면,
FA=2m×2Rω2=4mRω2,
FB=m×Rω2=mRω2이므로
구심력의 크기는 A가 B의 4배이다. (X)
따라서 정답은 3번이다.
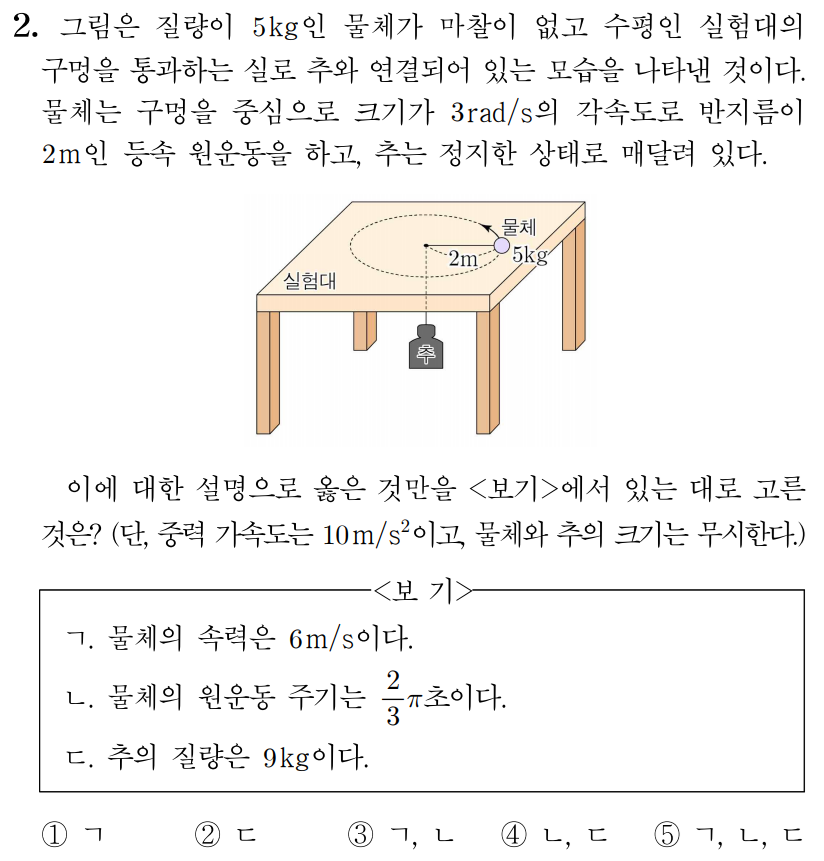
정답: $5$
ㄱ. 물체의 회전 반지름과 각속도의 크기는 각각 2m, 3rad/s이므로
물체의 속력은 2m×3rad/s=6m/s이다. (O)
ㄴ. 원운동 주기를 T라 할 때, 물체의 각속도의 크기 ω=T2πrad이므로,
3rad/s=T2πrad,
3=T2πs,
3T=2πs,
T=32πs(초)이다. (O)
ㄷ. 물체의 구심 가속도의 크기는 2m(6m/s)2=18m/s2이므로
구심력의 크기는 5kg×18m/s2=90kg⋅m/s2=90N이다.
이때 물체에 작용하는 구심력은 물체에 작용하는 장력과 같으며, 장력의 크기는 추에 작용하는 중력의 크기와 같다.
그러므로 추의 질량을 m이라 할 때,
90N=m×10m/s2,
90kg⋅m/s2=m×10m/s2,
90kg=m×10,
m=9kg이다. (O)
따라서 정답은 5번이다.