이상 기체는 아래와 같은 특징을 갖는다.
1. 이상 기체 법칙인 PV=nRT를 만족한다.
2. 이상 기체 분자의 크기를 무시하고, 분자 간 작용하는 힘이 없다.
3. 이상 기체 분자는 완전 탄성 충돌을 한다.
4. 이상 기체 분자는 무작위 운동을 한다.
5. 이상 기체 분자에 작용하는 중력은 무시한다.
기체 상수를 R, 아보가드로 수를 NA라 할 때, NAR의 값이다. 기호로는 kB로 나타낸다. (kB=1.38×10−23J/K)
NAR=kB, R=NAkB이므로 이상 기체의 몰 수를 n이라 할 때,
이상 기체 법칙 PV=nRT에 넣으면 PV=nNAkBT이다.
이때 이상 기체의 분자가 총 N개 있을 때 N=nNA이므로
PV=nRT는 PV=NkBT로도 나타낼 수 있다.
어느 물리량의 평균은 기호 위에 가로 막대기를 그려 표기한다.
예를 들어, 여러 물체의 속력 v가 다양하게 분포할 때, 평균 속력은 vˉ로 표기한다.
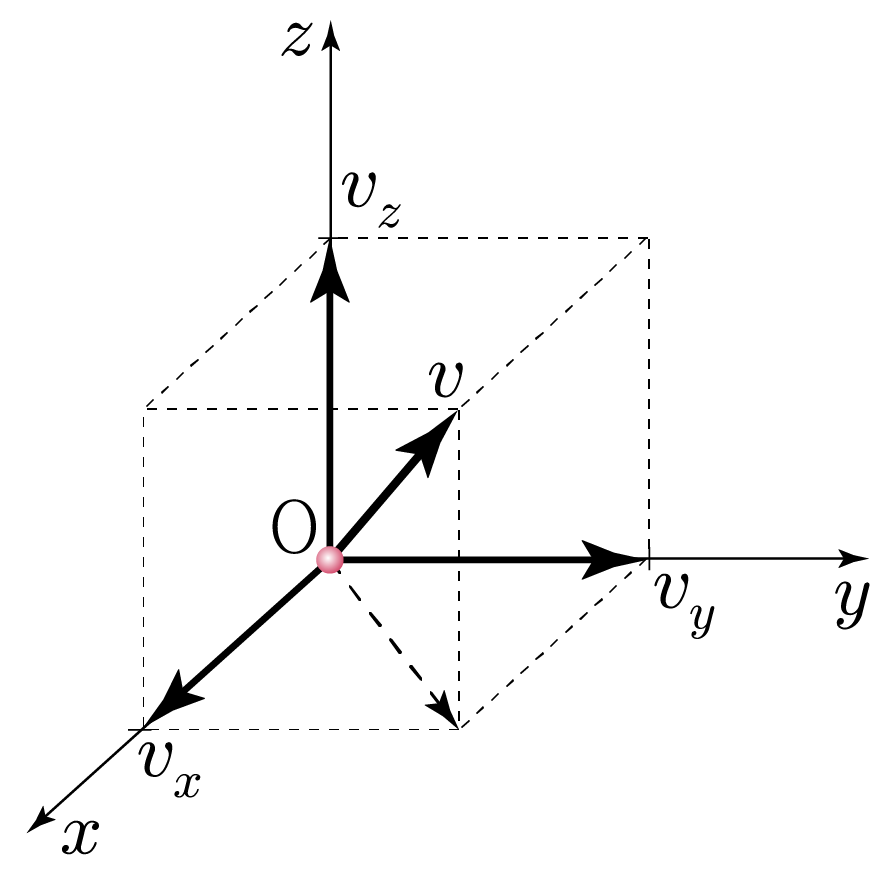
아래 그림과 같이 이상 기체 분자의 속도를 v라 할 때, x, y, z축에 나란한 속도 vx, vy, vz로 분해하면 v2=vx2+vy2+vz2를 만족한다.
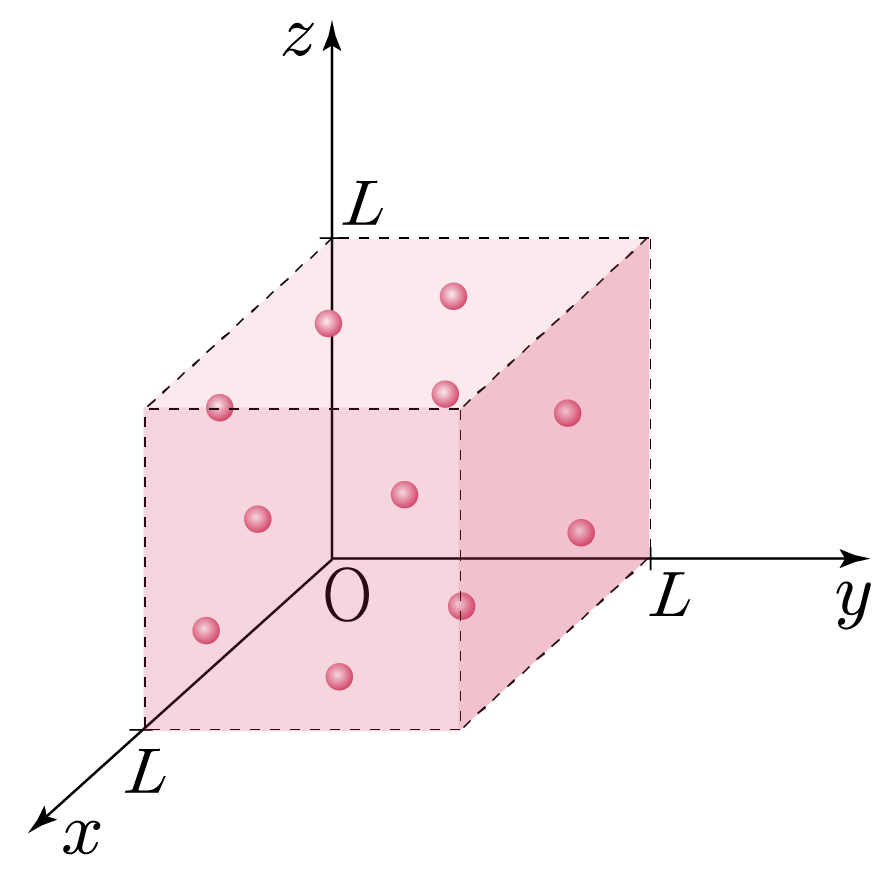
xyz 좌표(좌표 공간)에 한 변의 길이가 L인 정육면체 용기에 어느 이상 기체가 들어 있다고 가정할 때, 아래 그림과 같이 나타낼 수 있다.
이상 기체 분자는 방향에 관계없이 무작위 운동을 하므로 이상 기체 분자 전체로 보았을 때
vˉx2=vˉy2=vˉz2이다.
그러므로 vˉ2=vˉx2+vˉy2+vˉz2에서
vˉ2=vˉx2+vˉx2+vˉx2=3vˉx2,
vˉx2=31vˉ2이다.⋯①
이상 기체 분자의 운동을 통해 이상 기체의 평균 속력과 절대 온도 T의 관계를 유도해 보자.
1. 충격량을 통해 압력과의 관계식 구하기:
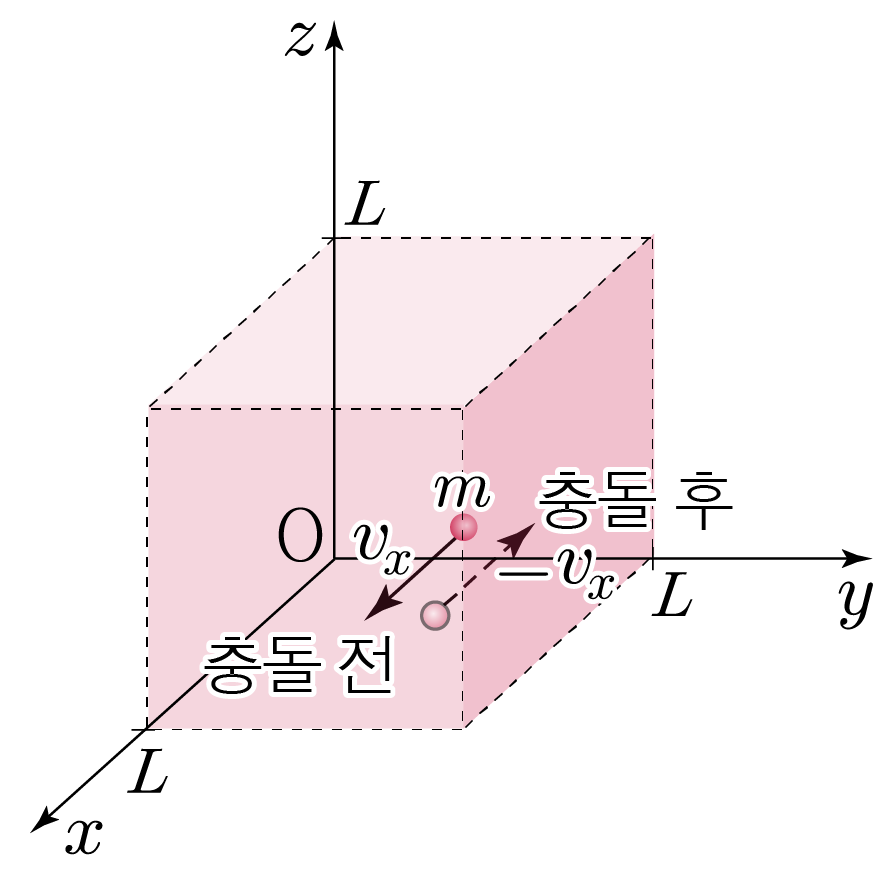
아래 그림과 같이 이상 기체 분자 1개의 질량을 m, x축에 나란한 속도를 vx라 할 때,
이상 기체 분자는 완전 탄성 충돌하므로 벽과 충돌 후 x축에 나란한 속도는 −vx이다.
따라서 이상 기체 분자 1개가 벽과 충돌할 때, 벽이 받은 충격량의 크기는 운동량 변화량의 크기와 같은 2m∣vx∣이다.
충돌 직후 이상 기체 분자는 반대 방향으로 운동하여 반대편 벽까지 이동하는 데 걸린 시간은 ∣vx∣L이고,
반대편 벽에 충돌한 직후부터 다시 처음에 충돌했던 벽까지 되돌아오는 데 걸린 시간은 ∣vx∣L이다.
그러므로 이상 기체 분자가 벽에 충돌한 후 다시 해당 벽으로 되돌아 오는 데 걸린 시간은 ∣vx∣L+∣vx∣L=∣vx∣2L이고,
1초당 이상 기체 분자 1개가 벽을 충돌한 횟수는 2L∣vx∣이다.
이를 통해 이상 기체 분자 1개로부터 1초당 벽이 받은 충격량의 크기는 2m∣vx∣×2L∣vx∣=Lm∣vx∣2=Lmvx2임을 알 수 있다.
vx2는 vx의 부호와 관계없이 항상 양수이기 때문에 ∣vx∣2=vx2이다.
이상 기체 분자가 총 N개 있고, 평균 속력을 vˉ라 할 때,
이상 기체 분자 전체로부터 1초당 벽이 받은 충격량의 크기는 LNmvˉx2이다.
①에 의해 vˉx2=31vˉ2이므로 LNmvˉx2=3LNmvˉ2이다.
1초당 벽이 받은 충격량(충격량 공식 Ft를 시간 t로 나눈 값)은 힘과 같으므로 한 벽에 가해진 힘은 3LNmvˉ2이다.
이때 압력은 가해진 힘을 단면적으로 나눈 값이므로 이상 기체가 한 벽에 가하는 압력 P는
3LNmvˉ2를 한 벽의 단면적인 L2으로 나눈 P=L23LNmvˉ2=3L3Nmvˉ2이다.
이상 기체 분자는 방향에 관계없이 무작위 운동을 하므로 이상 기체가 각각의 벽에 가하는 압력은 P=3L3Nmvˉ2로 같다.
따라서 이상 기체의 압력 P=3L3Nmvˉ2이다.
용기의 부피(이상 기체의 부피)를 V라 할 때, V=L3이므로 P=3L3Nmvˉ2=3VNmvˉ2이다.
2. 구한 압력을 PV=nRT에 대입하기:
볼츠만 상수를 kB, 이상 기체의 절대 온도를 T라 하면 PV=NkBT이다.
여기에 P=3VNmvˉ2를 넣으면
3VNmvˉ2×V=NkBT,
3Nmvˉ2=NkBT,
3mvˉ2=kBT,
vˉ2=m3kBT,
vˉ=m3kBT이다.
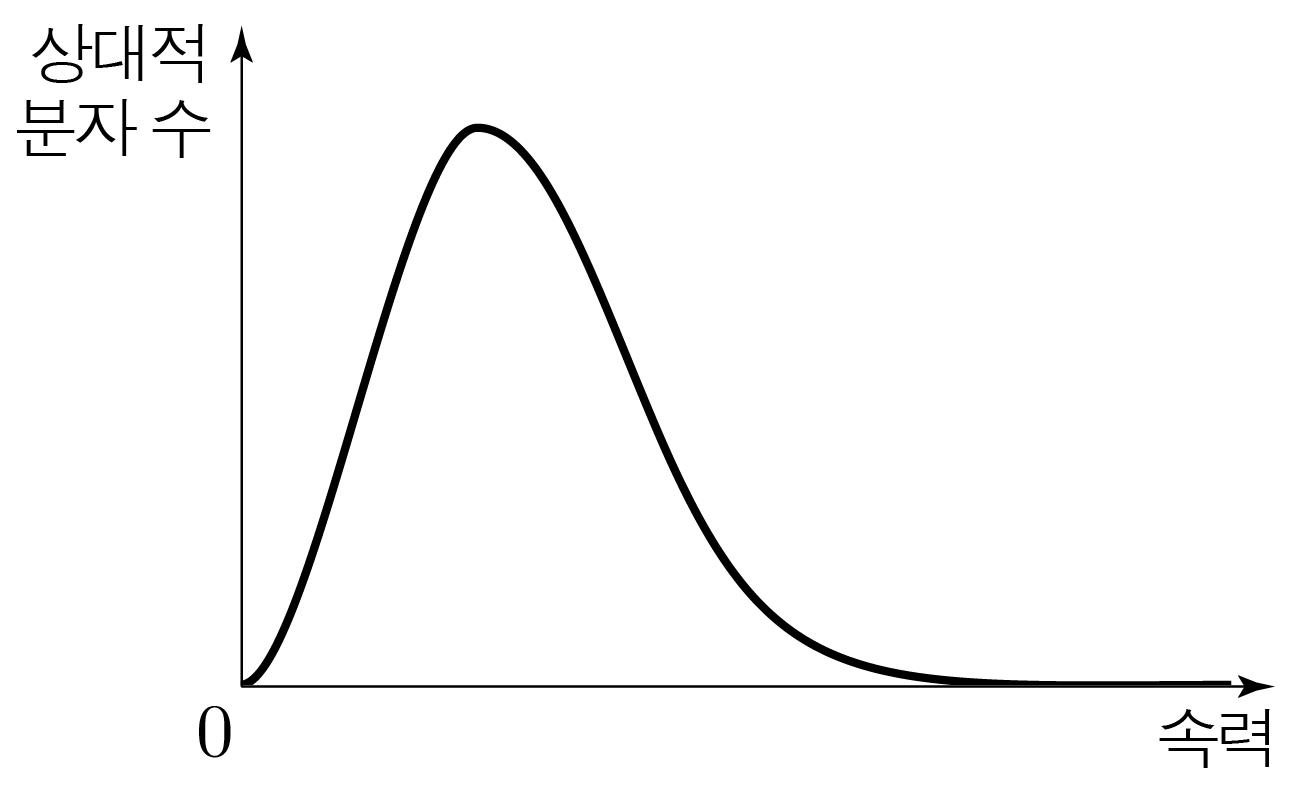
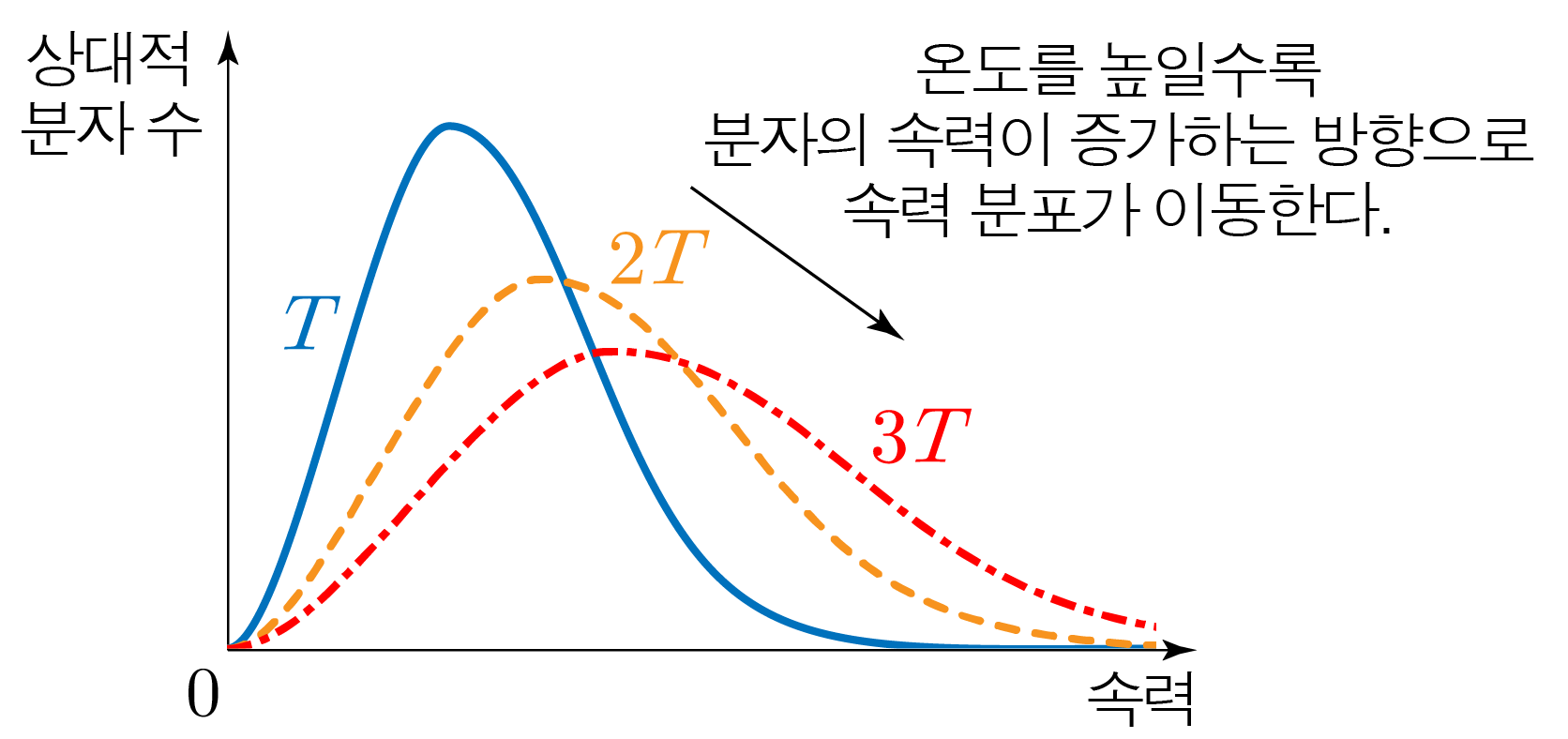
아래 그림과 같이 이상 기체 분자의 속력 분포를 분자 수–속력 그래프로 나타낸 것이다.
분자 수-속력 그래프에서 아래 면적은 이상 기체의 분자 수에 정비례(두 값이 같은 비율로 변화)한다.
이상 기체 분자의 평균 속력 vˉ=m3kBT이므로,
이상 기체의 온도를 높이면 분자의 속력이 증가하는 방향으로 속력 분포가 이동한다.
기체를 이루는 분자들의 운동 에너지와 퍼텐셜 에너지의 총합이다.
기본 단위는 J이고, 기호로는 U로 나타낸다.
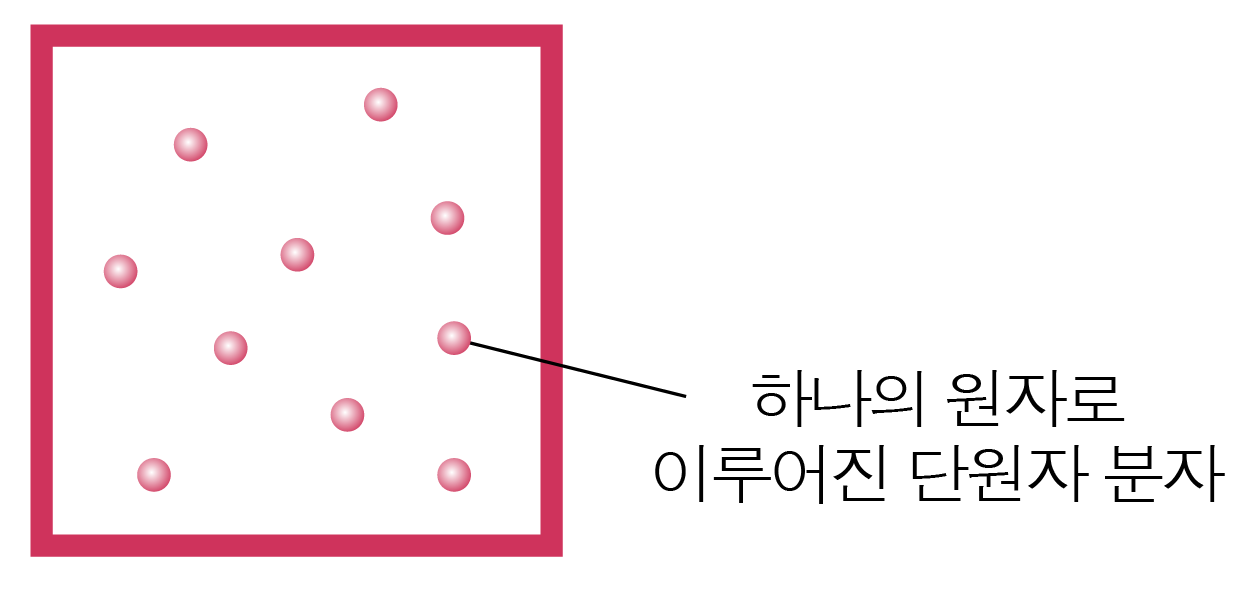
아래 그림과 같이 단원자 분자(하나의 원자로 이루어진 분자)의 경우 하나의 점으로 보아 진동 등을 고려하지 않아도 되고,
분자 간 작용하는 힘이 없으며 중력은 무시하므로 퍼텐셜 에너지는 0이다.
따라서 단원자 분자 이상 기체의 내부 에너지는 단원자 분자들의 운동 에너지의 합과 같다.
단원자 분자 이상 기체의 분자가 총 N개 있고, 평균 속력을 vˉ, 이상 기체 분자 1개의 질량을 m이라 하면, 내부 에너지 U는
U=N×21mvˉ2이다.
볼츠만 상수를 kB, 이상 기체의 절대 온도를 T라 하면, vˉ=m3kBT이므로
이를 U=N×21mvˉ2에 넣으면
U=N×21m×m3kBT,
U=23NkBT이다.
kB=NAR이므로 이를 U=23NkBT에 넣으면
U=23N×NAR×T,
U=2NA3NRT이다.
이상 기체의 몰 수를 n이라 할 때,
N=nNA,
NAN=n이므로
이를 U=2NA3NRT에 넣으면
U=23nRT이다.
따라서 단원자 분자 이상 기체의 내부 에너지는 23nRT이다.
정답: $2$
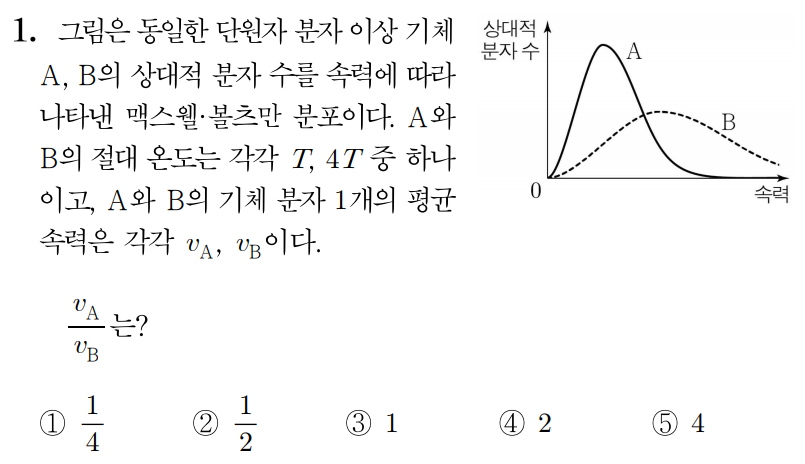
이상 기체의 온도를 높이면, 맥스웰·볼츠만 분포에서 분자의 속력이 증가하는 방향으로 속력 분포가 이동하므로
A, B의 절대 온도는 각각 T, 4T이다.
이상 기체 분자의 평균 속력 vˉ=m3kBT이므로 A와 B의 분자 1개의 질량을 m, 볼츠만 상수를 kB라 하면,
vA=m3kBT, vB=m3kB×4T=2m3kBT이다.
그러므로 vBvA=2m3kBTm3kBT=21이다.
따라서 정답은 2번이다.

정답: $5$
ㄱ. A와 B의 분자 수는 같으므로 A와 B의 몰 수를 n이라 하고, A, B의 절대 온도를 각각 T, TB라 하면,
A와 B에서 각각 이상 기체 법칙을 적용하면 아래와 같다.
A에서 P0V=nRT이고,
B에서 P0×2V=nRTB, 2P0V=nRTB이다.
P0V=nRT이므로
2P0V=2nRT=nRTB,
TB=2T이다.
그러므로 기체의 절대 온도는 B가 A의 2배이다. (O)
ㄴ. 이상 기체 분자의 평균 속력 vˉ=m3kBT이므로 A와 B의 기체 분자 1개의 평균 속력을 각각 vˉA, vˉB라 하면,
vˉA=2m3kBT, vˉB=m3kB×(2T)=22m3kBT이다.
그러므로 기체 분자 1개의 평균 속력은 B가 A의 2배이다. (O)
ㄷ. 단원자 분자 이상 기체의 내부 에너지 U=23nRT이므로 A와 B의 내부 에너지를 각각 UA, UB라 하면,
UA=23nRT, UB=23nR×2T=3nRT이다.
그러므로 내부 에너지는 B가 A의 2배이다. (O)
따라서 정답은 5번이다.