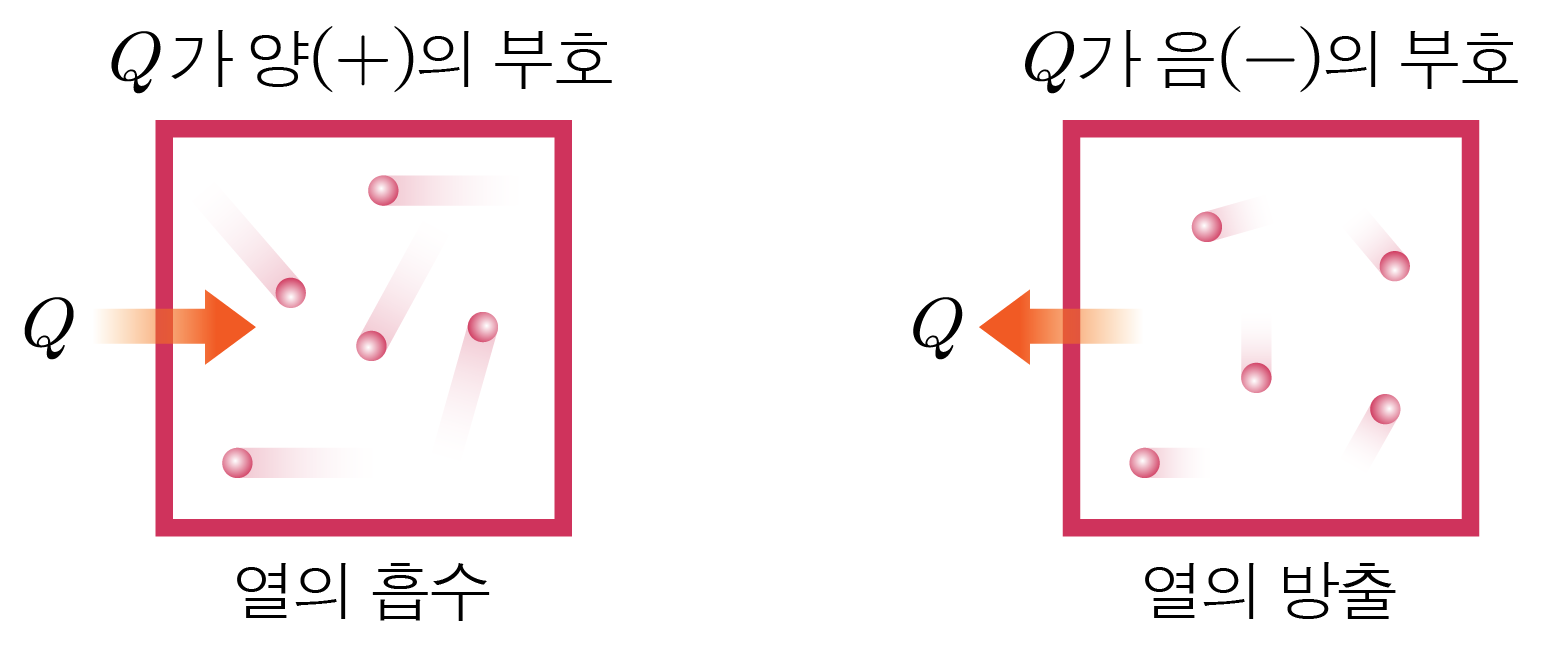
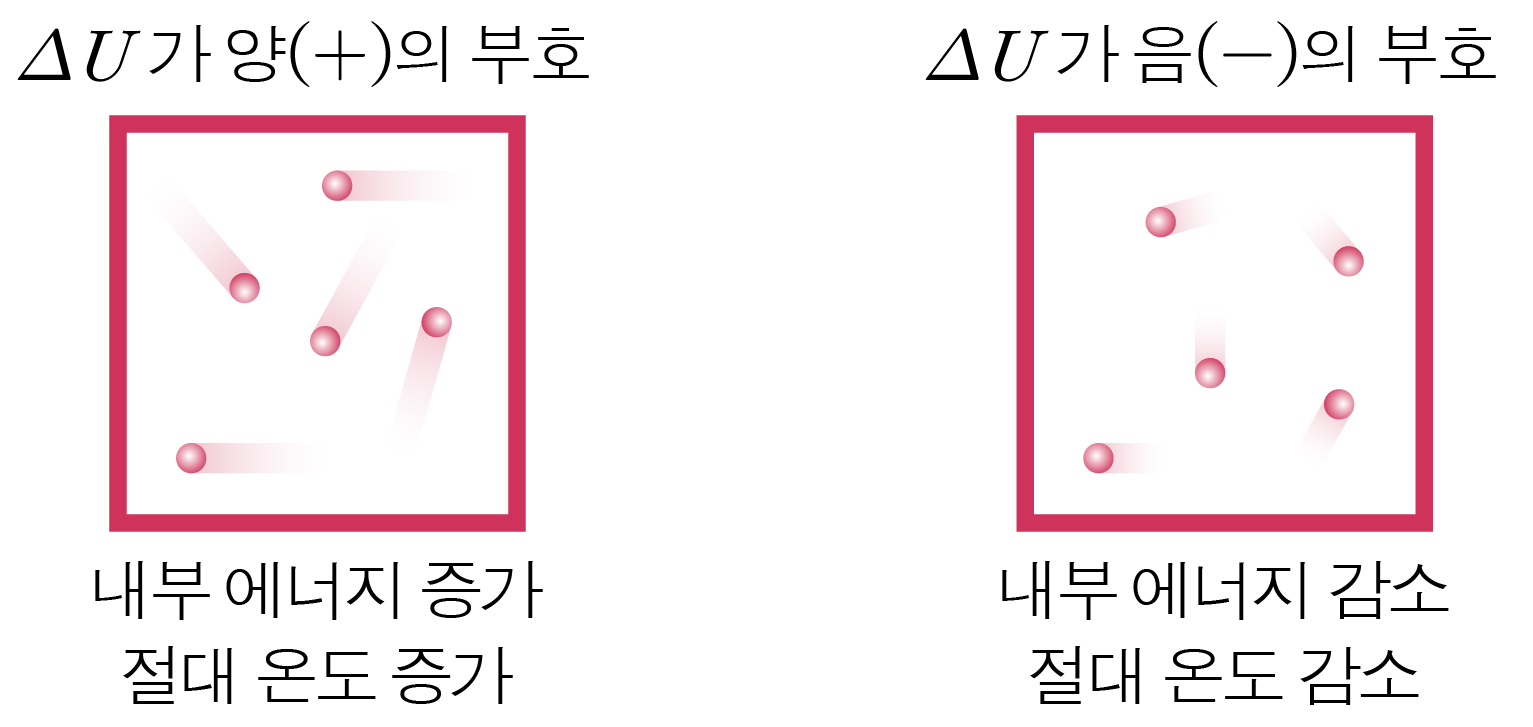
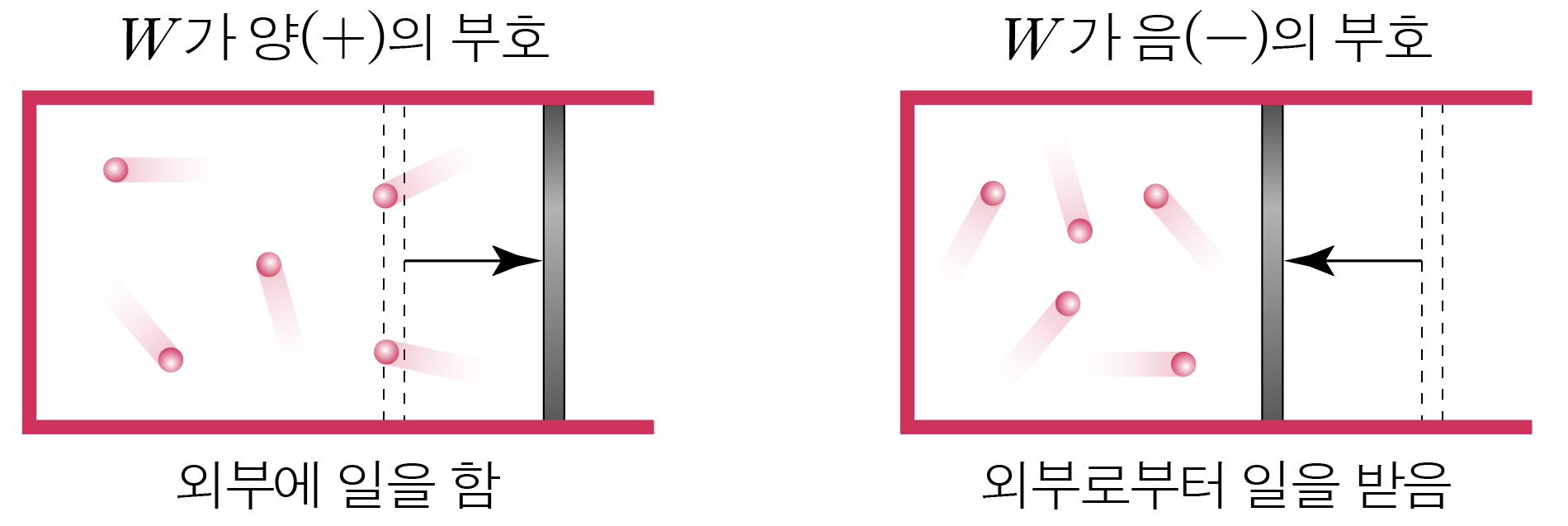
열량을 Q , Q , Δ U , Δ U , W W Q = Δ U + W Q = Δ U + W
열량(Q Q + + − −
내부 에너지 변화(Δ U Δ U + + − −
일(W W + + − −
기체의 물리량이 한 상태에서 다른 상태로 변하는 과정이다.
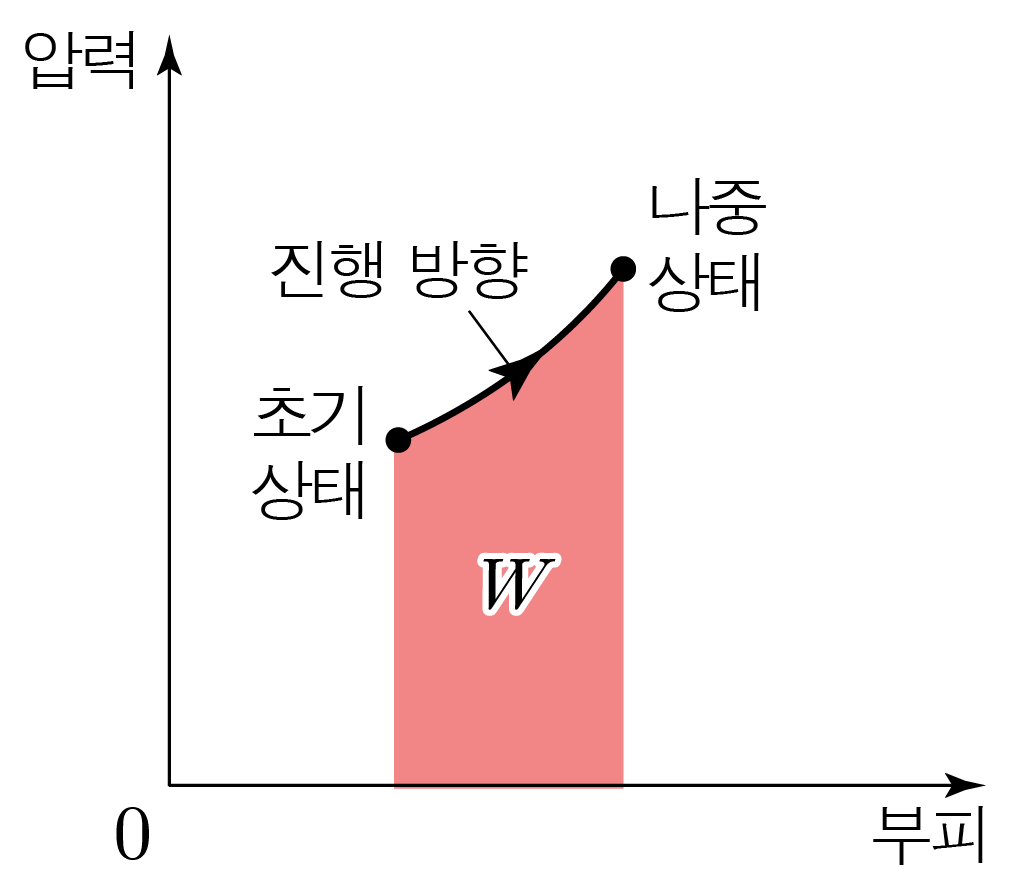
열역학 과정은 주로 압력-부피(P − V P − V W W
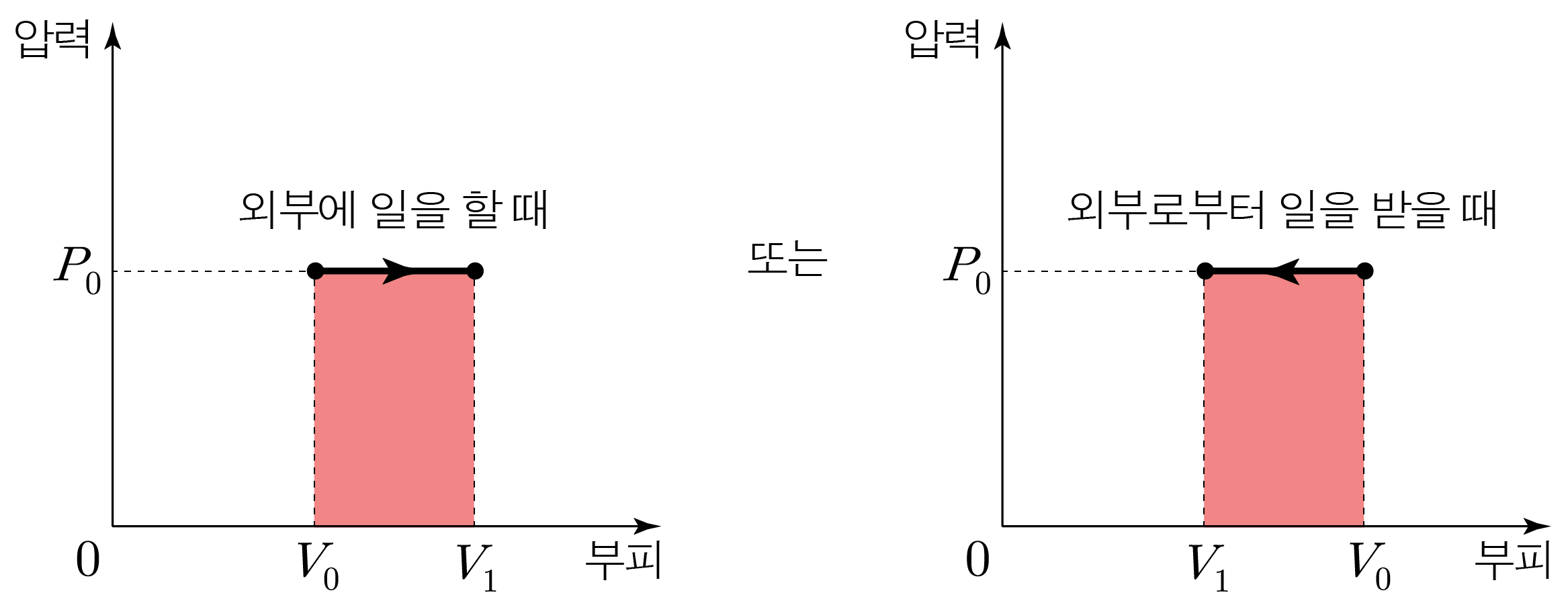
압력이 일정한 과정이다.P P Δ V Δ V W = P Δ V W = P Δ V
단원자 분자 이상 기체의 내부 에너지는 3 2 n R T 2 3 n R T P V = n R T P V = n R T 3 2 n R T = 3 2 P V 2 3 n R T = 2 3 P V
등압 과정에서 부피 변화를 Δ V Δ V Δ U = 3 2 P Δ V , Δ U = 2 3 P Δ V , W = P Δ V W = P Δ V Q = 3 2 P Δ V + P Δ V = 5 2 P Δ V Q = 2 3 P Δ V + P Δ V = 2 5 P Δ V
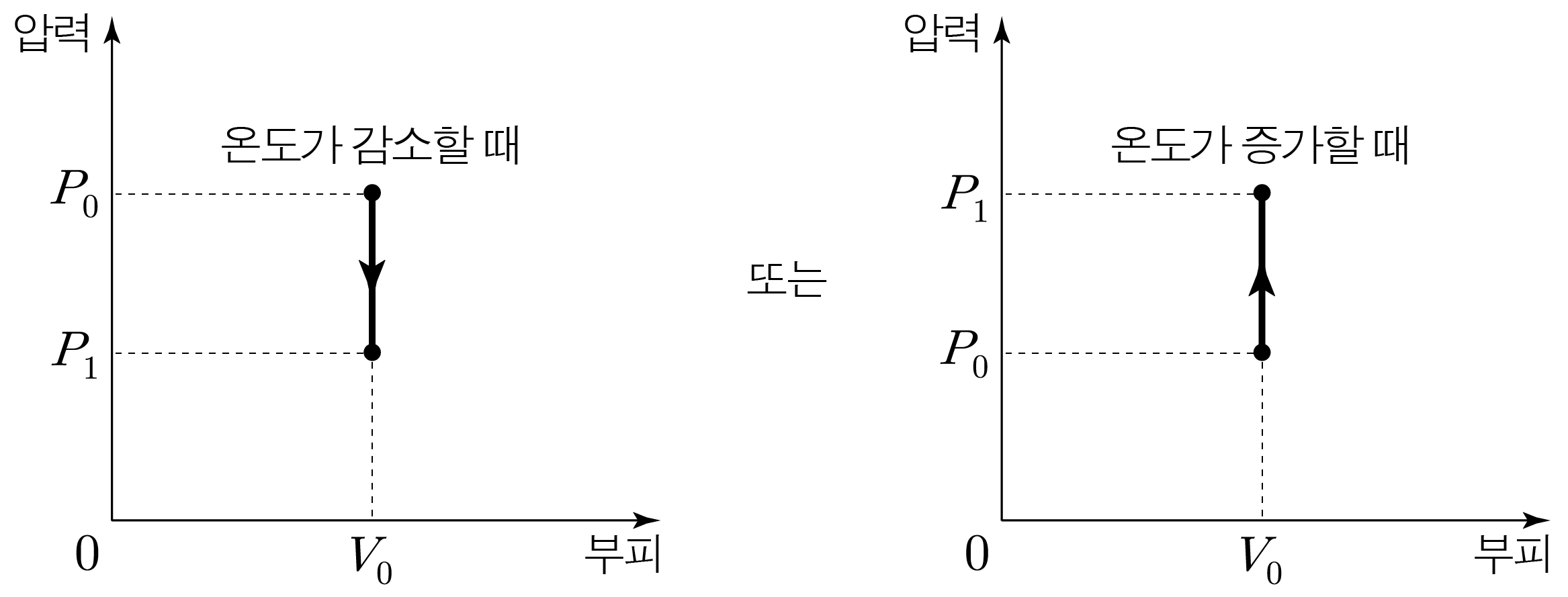
부피가 일정한 과정이다. 부피 변화가 없기 때문에 W = 0 W = 0 Q = Δ U Q = Δ U
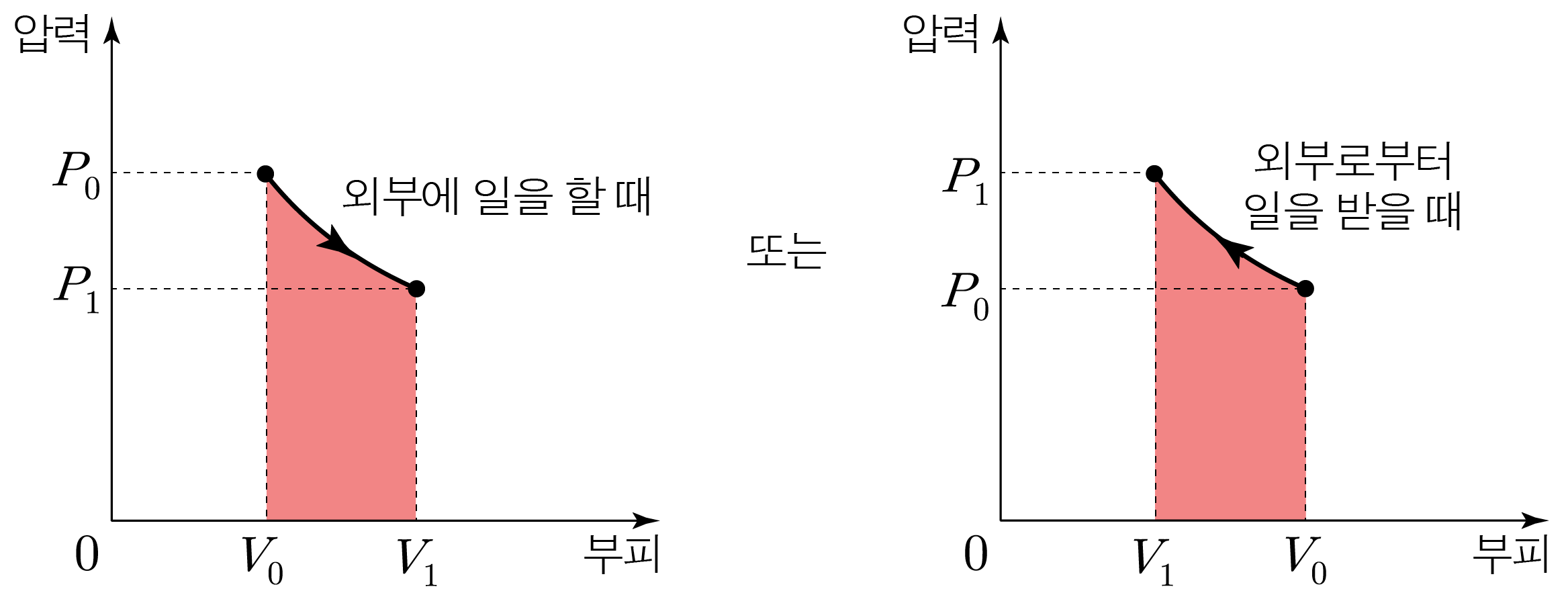
온도가 일정한 과정이다. 온도 변화가 없기 때문에 Δ U = 0 Δ U = 0 Q = W Q = W
일정한 양의 이상 기체가 등온 과정을 거칠 때, 이상 기체 법칙 P V = n R T P V = n R T n n T T P V P V
$P_0V_0=P_1V_1$이다.
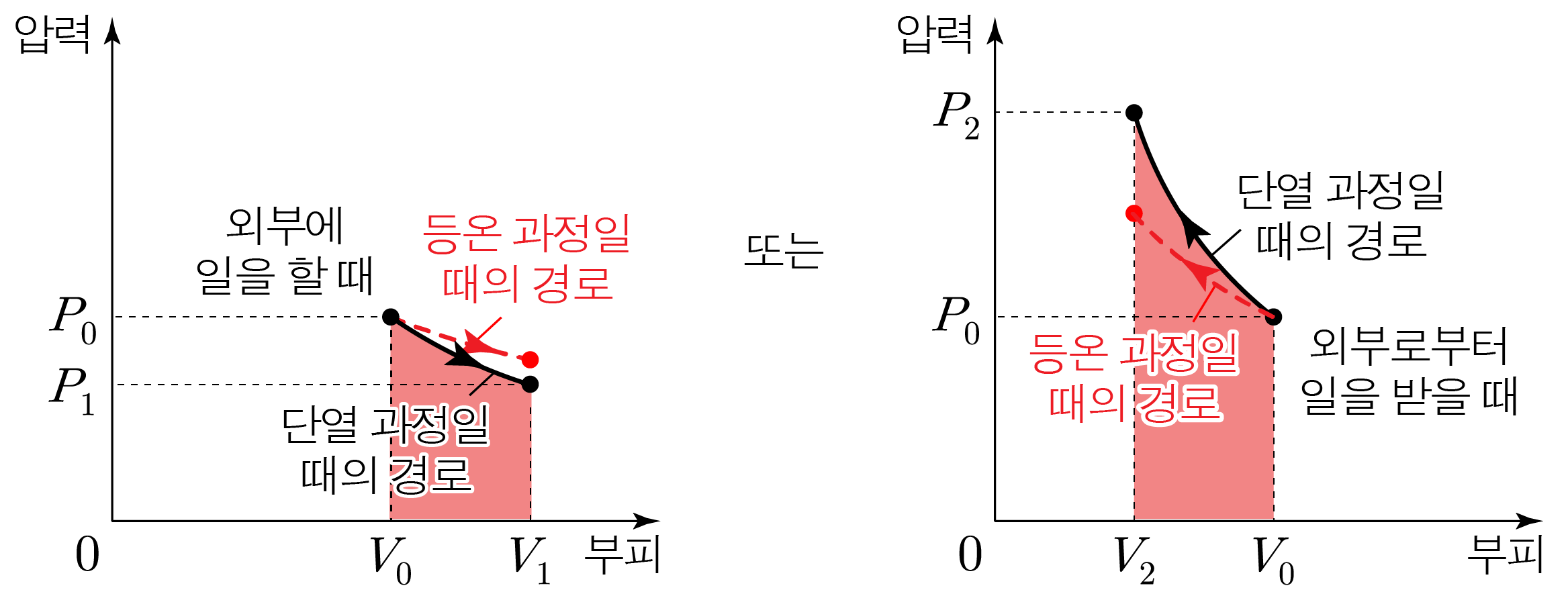
Q = 0 Q = 0 Q = 0 Q = 0 Δ U + W = 0 Δ U + W = 0
기체가 외부에 일을 하는 경우와 기체가 외부로부터 일을 받는 경우를 나눠 물리량의 변화를 분석하면 아래와 같다.
기체가 외부에 일을 하는 경우(W > 0 W > 0 Δ U < 0 Δ U < 0 P V = n R T P V = n R T n n T T P V P V
기체가 외부로부터 일을 받는 경우(W < 0 W < 0 Δ U > 0 Δ U > 0 P V = n R T P V = n R T n n T T P V P V
$P_1V_1 \lt P_0V_0 \lt P_2V_2$이다.
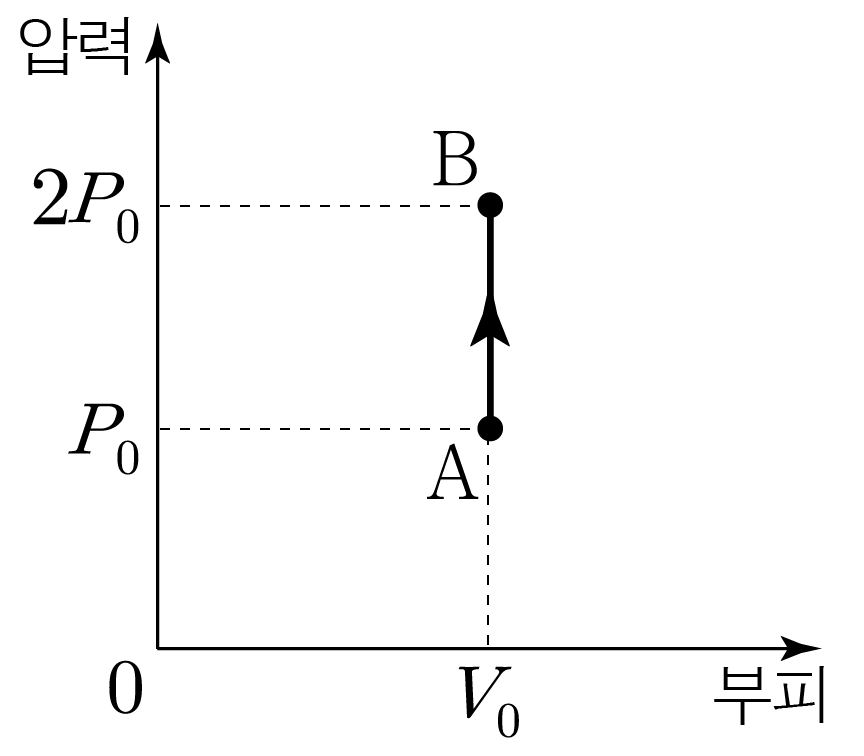
그림은 일정량의 단원자 분자 이상 기체가 상태 A → B A → B A → B A → B A → B A → B
A → B A → B
이상 기체의 몰 수를 n , n , R , R , T T 3 2 n R T 2 3 n R T P V = n R T P V = n R T 3 2 n R T = 3 2 P V 2 3 n R T = 2 3 P V
그러므로 A A 3 2 P 0 V 0 2 3 P 0 V 0 B B 3 2 × 2 P 0 × V 0 = 3 P 0 V 0 2 3 × 2 P 0 × V 0 = 3 P 0 V 0
A → B A → B Δ U = 3 P 0 V 0 − 3 2 P 0 V 0 = 3 2 P 0 V 0 Δ U = 3 P 0 V 0 − 2 3 P 0 V 0 = 2 3 P 0 V 0
A → B A → B W = 0 W = 0 Q = Δ U + W = 3 2 P 0 V 0 + 0 = 3 2 P 0 V 0 Q = Δ U + W = 2 3 P 0 V 0 + 0 = 2 3 P 0 V 0
Q > 0 Q > 0 A → B A → B 3 2 P 0 V 0 2 3 P 0 V 0
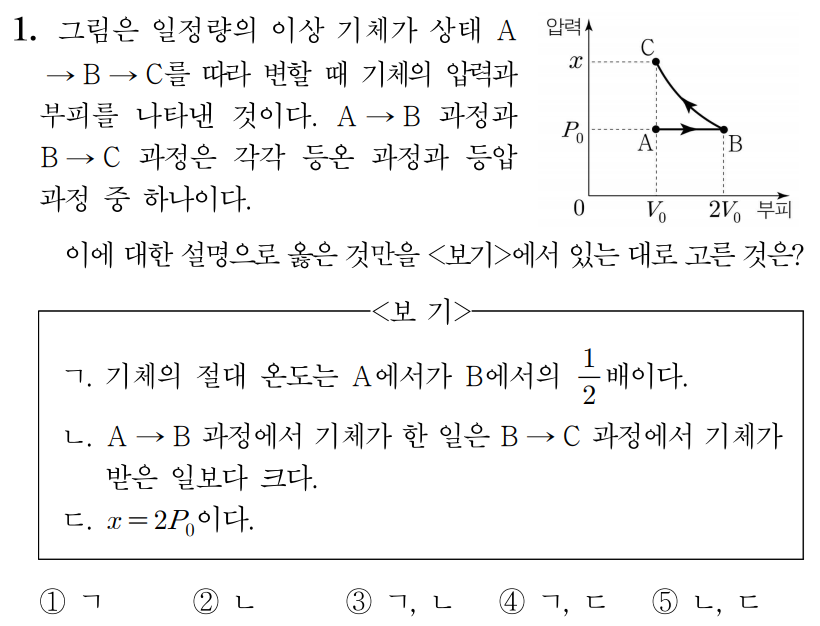
1번 문항 정답 및 해설 보기
정답: $4$
ㄱ. 기체의 몰 수를 n , n , A , A , B B T A , T A , T B T B A A B B A A P 0 V 0 = n R T A P 0 V 0 = n R T A B B P 0 × 2 V 0 = n R T B , P 0 × 2 V 0 = n R T B , 2 P 0 V 0 = n R T B 2 P 0 V 0 = n R T B T B = 2 T A , T B = 2 T A , T A = 1 2 T B T A = 2 1 T B A A B B 1 2 2 1
ㄴ. 압력-부피(P − V P − V W W A → B A → B B → C B → C
ㄷ. A → B A → B B → C B → C
등온 과정을 거칠 때, 이상 기체 법칙 P V = n R T P V = n R T n n T T P V P V
그러므로 x × V 0 = P 0 × 2 V 0 , x × V 0 = P 0 × 2 V 0 , x = 2 P 0 x = 2 P 0
따라서 정답은 4 4
2번 문항 정답 및 해설 보기
정답: $4$
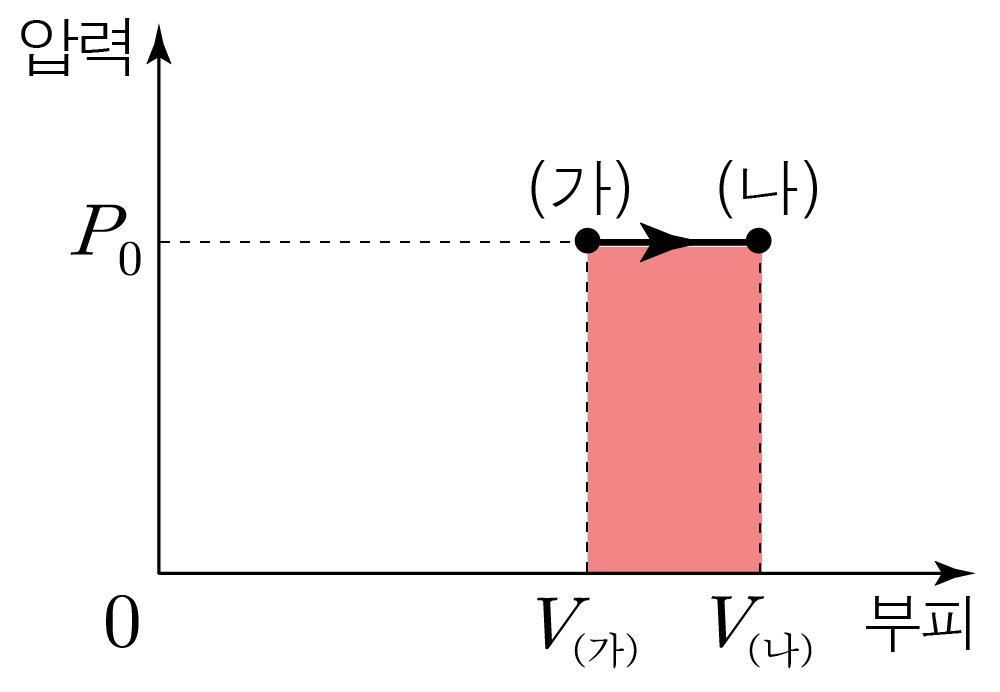
(가) → → Δ U Δ U
단원자 분자 이상 기체의 내부 에너지는 3 2 n R T 2 3 n R T 3 2 × 1 × R × 5 T = 15 2 R T , 2 3 × 1 × R × 5 T = 2 1 5 R T , 3 2 × 1 × R × 7 T = 21 2 R T 2 3 × 1 × R × 7 T = 2 2 1 R T Δ U = 21 2 R T − 15 2 R T = 3 R T Δ U = 2 2 1 R T − 2 1 5 R T = 3 R T
이제 (가) → → W W
(가), (나)에서 기체의 부피를 각각 V ( 가 ) V ( 가 ) V ( 나 ) V ( 나 )
그래프 아래 면적이 W W W = P 0 ( V ( 나 ) − V ( 가 ) ) W = P 0 ( V ( 나 ) − V ( 가 ) )
(가)와 (나)에서 이상 기체 법칙을 각각 적용하면
(가)에서 P 0 V ( 가 ) = 1 × R × 5 T , P 0 V ( 가 ) = 1 × R × 5 T , P 0 V ( 가 ) = 5 R T , P 0 V ( 가 ) = 5 R T , V ( 가 ) = 5 R T P 0 V ( 가 ) = P 0 5 R T
(나)에서 P 0 V ( 나 ) = 1 × R × 7 T , P 0 V ( 나 ) = 1 × R × 7 T , P 0 V ( 나 ) = 7 R T , P 0 V ( 나 ) = 7 R T , V ( 나 ) = 7 R T P 0 V ( 나 ) = P 0 7 R T
그러므로 V ( 나 ) − V ( 가 ) = 7 R T P 0 − 5 R T P 0 = 2 R T P 0 V ( 나 ) − V ( 가 ) = P 0 7 R T − P 0 5 R T = P 0 2 R T
이를 ①에 넣으면 W = P 0 ( V ( 나 ) − V ( 가 ) ) W = P 0 ( V ( 나 ) − V ( 가 ) ) W = P 0 × 2 R T P 0 = 2 R T W = P 0 × P 0 2 R T = 2 R T Q = Δ U + W Q = Δ U + W Q = 3 R T + 2 R T = 5 R T Q = 3 R T + 2 R T = 5 R T
따라서 정답은 4 4