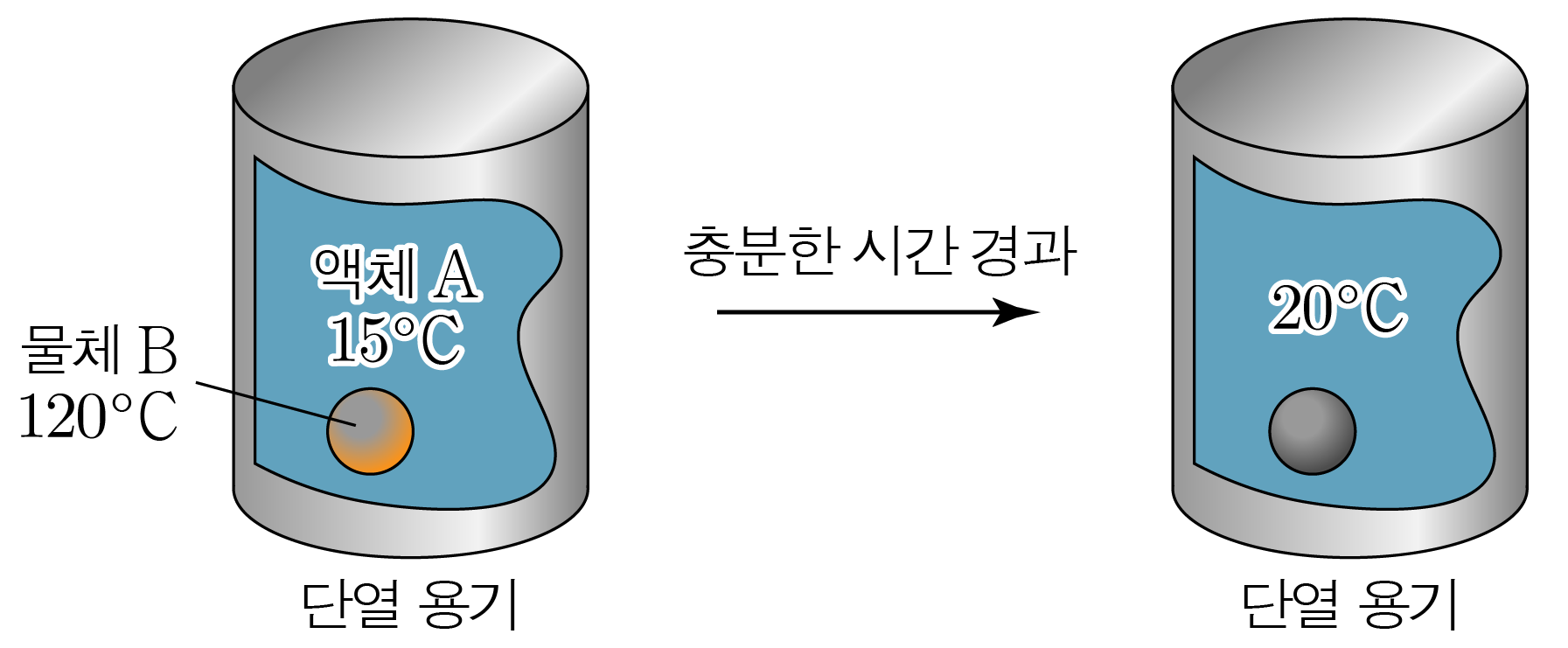
열의 이동으로 두 물체의 온도가 같아져 더 이상 열이 이동하지 않아 온도가 변하지 않는 것이다.
그림은 온도가 15 ∘ C 1 5 ∘ C 2 k g 2 k g A A 120 ∘ C 1 2 0 ∘ C 1 k g 1 k g B B A A B B 20 ∘ C 2 0 ∘ C A A B B 4000 J / k g ⋅ K 4 0 0 0 J / k g ⋅ K c B c B c B c B A A B B
온도는 B B A A B B A A A A B B
A A Q A Q A A A c A c A m A m A ∣ Δ T A ∣ ∣ Δ T A ∣ Q A = c A m A ∣ Δ T A ∣ , Q A = c A m A ∣ Δ T A ∣ , Q A = 4000 J / k g ⋅ K × 2 k g × ( 20 ∘ C − 15 ∘ C ) , Q A = 4 0 0 0 J / k g ⋅ K × 2 k g × ( 2 0 ∘ C − 1 5 ∘ C ) , Q A = 4000 J / k g ⋅ K × 2 k g × 5 ∘ C Q A = 4 0 0 0 J / k g ⋅ K × 2 k g × 5 ∘ C
이때 동일한 온도만큼 변했을 때, 변화의 크기는 섭씨 온도와 절대 온도가 같으므로 5 ∘ C 5 ∘ C 5 K 5 K Q A = 4000 J / k g ⋅ K × 2 k g × 5 K , Q A = 4 0 0 0 J / k g ⋅ K × 2 k g × 5 K , Q A = 8000 J / K × 5 K , Q A = 8 0 0 0 J / K × 5 K , Q A = 40000 J Q A = 4 0 0 0 0 J
B B Q B Q B B B m B m B ∣ Δ T B ∣ ∣ Δ T B ∣ Q B = c B m B ∣ Δ T B ∣ , Q B = c B m B ∣ Δ T B ∣ , Q B = c B × 1 k g × ( 120 ∘ C − 20 ∘ C ) , Q B = c B × 1 k g × ( 1 2 0 ∘ C − 2 0 ∘ C ) , Q B = c B × 1 k g × 100 ∘ C Q B = c B × 1 k g × 1 0 0 ∘ C
이때 동일한 온도만큼 변했을 때, 변화의 크기는 섭씨 온도와 절대 온도가 같으므로 100 ∘ C 1 0 0 ∘ C 100 K 1 0 0 K Q B = c B × 1 k g × 100 K , Q B = c B × 1 k g × 1 0 0 K , Q B = c B × 100 k g ⋅ K Q B = c B × 1 0 0 k g ⋅ K
A A B B Q A = Q B Q A = Q B 40000 J = c B × 100 k g ⋅ K , 4 0 0 0 0 J = c B × 1 0 0 k g ⋅ K , 400 J = c B k g ⋅ K , 4 0 0 J = c B k g ⋅ K , 400 J / k g ⋅ K = c B , 4 0 0 J / k g ⋅ K = c B , c B = 400 J / k g ⋅ K c B = 4 0 0 J / k g ⋅ K
A A B B B B C C A A C C
체온계가 사람과 열평형 상태라면, 체온계의 온도를 통해 사람의 체온을 알 수 있다.
1번 문항 정답 및 해설 보기
정답: $5$
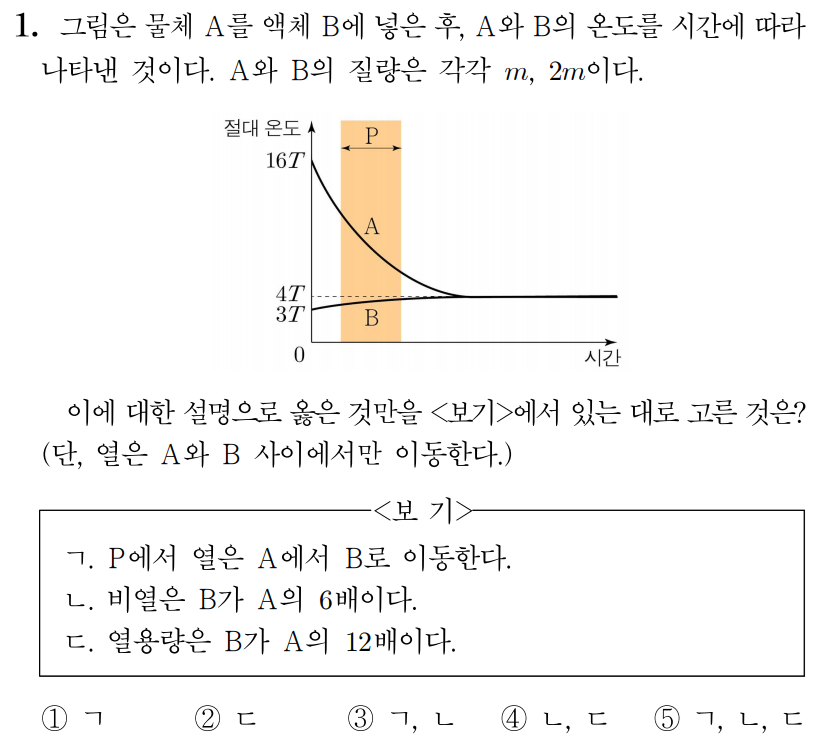
ㄱ. P P A A B B A A B B
ㄴ. 열은 A A B B A A B B
A A Q A Q A A A c A c A m A m A ∣ Δ T A ∣ ∣ Δ T A ∣ Q A = c A m A ∣ Δ T A ∣ , Q A = c A m A ∣ Δ T A ∣ , Q A = c A × m × ( 16 T − 4 T ) , Q A = c A × m × ( 1 6 T − 4 T ) , Q A = c A × m × 12 T , Q A = c A × m × 1 2 T , Q A = 12 c A m T Q A = 1 2 c A m T
B B Q B Q B B B c B c B m B m B ∣ Δ T B ∣ ∣ Δ T B ∣ Q B = c B m B ∣ Δ T B ∣ , Q B = c B m B ∣ Δ T B ∣ , Q B = c B × 2 m × ( 4 T − 3 T ) , Q B = c B × 2 m × ( 4 T − 3 T ) , Q B = c B × 2 m × T , Q B = c B × 2 m × T , Q B = 2 c B m T Q B = 2 c B m T
A A B B Q A = Q B Q A = Q B 12 c A m T = 2 c B m T , 1 2 c A m T = 2 c B m T , 12 c A = 2 c B , 1 2 c A = 2 c B , 6 c A = c B 6 c A = c B B B A A 6 6
ㄷ. 열용량 C = c m C = c m A A C A = c A × m = c A m C A = c A × m = c A m B B C B = c B × 2 m = 2 c B m C B = c B × 2 m = 2 c B m
이때 c B = 6 c A c B = 6 c A C B = 2 c B m = 2 × 6 c A × m = 12 c A m C B = 2 c B m = 2 × 6 c A × m = 1 2 c A m B B A A 12 1 2
따라서 정답은 5 5
2번 문항 정답 및 해설 보기
정답: $2$
열은 A A B B A A B B
A A Q A Q A A A c A c A m A m A ∣ Δ T A ∣ ∣ Δ T A ∣ Q A = c A m A ∣ Δ T A ∣ , Q A = c A m A ∣ Δ T A ∣ , Q A = 4000 J / k g ⋅ K × 5 k g × ( T − 22 ∘ C ) , Q A = 4 0 0 0 J / k g ⋅ K × 5 k g × ( T − 2 2 ∘ C ) , Q A = 20000 J / K × ( T − 22 ∘ C ) Q A = 2 0 0 0 0 J / K × ( T − 2 2 ∘ C )
B B Q B Q B B B c B c B m B m B ∣ Δ T B ∣ ∣ Δ T B ∣ Q B = c B m B ∣ Δ T B ∣ , Q B = c B m B ∣ Δ T B ∣ , Q B = 500 J / k g ⋅ K × 1 k g × ( 104 ∘ C − T ) , Q B = 5 0 0 J / k g ⋅ K × 1 k g × ( 1 0 4 ∘ C − T ) , Q B = 500 J / K × ( 104 ∘ C − T ) Q B = 5 0 0 J / K × ( 1 0 4 ∘ C − T )
A A B B Q A = Q B Q A = Q B 20000 J / K × ( T − 22 ∘ C ) = 500 J / K × ( 104 ∘ C − T ) , 2 0 0 0 0 J / K × ( T − 2 2 ∘ C ) = 5 0 0 J / K × ( 1 0 4 ∘ C − T ) , 20000 × ( T − 22 ∘ C ) = 500 × ( 104 ∘ C − T ) , 2 0 0 0 0 × ( T − 2 2 ∘ C ) = 5 0 0 × ( 1 0 4 ∘ C − T ) , 40 × ( T − 22 ∘ C ) = 104 ∘ C − T , 4 0 × ( T − 2 2 ∘ C ) = 1 0 4 ∘ C − T , 40 T − 880 ∘ C = 104 ∘ C − T , 4 0 T − 8 8 0 ∘ C = 1 0 4 ∘ C − T , 41 T = 984 ∘ C , 4 1 T = 9 8 4 ∘ C , T = 24 ∘ C T = 2 4 ∘ C
따라서 정답은 2 2