두 물체가 충돌할 때 충돌 후 상대 속도의 크기 충돌 전 상대 속도의 크기 충돌 전 상대 속도의 크기 충돌 후 상대 속도의 크기 e e
그림 (가)는 마찰이 없는 수평면에서 물체 A A B B v v 1 m / s 1 m / s A A B B A A B B 1 m / s 1 m / s 3 m / s 3 m / s A A B B 2 k g 2 k g 1 k g 1 k g v v e e
오른쪽 방향을 양( + ) ( + ) A A B B 2 k g × v + 1 k g × ( − 1 m / s ) , 2 k g × v + 1 k g × ( − 1 m / s ) , 2 v k g − 1 k g ⋅ m / s 2 v k g − 1 k g ⋅ m / s
충돌 후 A A B B 2 k g × 1 m / s + 1 k g × 3 m / s , 2 k g × 1 m / s + 1 k g × 3 m / s , 2 k g ⋅ m / s + 3 k g ⋅ m / s = 5 k g ⋅ m / s 2 k g ⋅ m / s + 3 k g ⋅ m / s = 5 k g ⋅ m / s
충돌하는 물체의 운동량의 합은 운동량 보존 법칙에 의해 충돌 전과 후가 같으므로2 v k g − 1 k g ⋅ m / s = 5 k g ⋅ m / s , 2 v k g − 1 k g ⋅ m / s = 5 k g ⋅ m / s , 2 v k g = 6 k g ⋅ m / s , 2 v k g = 6 k g ⋅ m / s , v k g = 3 k g ⋅ m / s , v k g = 3 k g ⋅ m / s , v = 3 m / s v = 3 m / s
충돌 전과 충돌 후의 A A B B
A A A A B B v B − v A v B − v A − 1 m / s − 3 m / s = − 4 m / s − 1 m / s − 3 m / s = − 4 m / s 3 m / s − 1 m / s = 2 m / s 3 m / s − 1 m / s = 2 m / s
B B B B A A v A − v B v A − v B 3 m / s − ( − 1 m / s ) = 4 m / s 3 m / s − ( − 1 m / s ) = 4 m / s 1 m / s − 3 m / s = − 2 m / s 1 m / s − 3 m / s = − 2 m / s
그러므로 A A B B 4 m / s 4 m / s 2 m / s 2 m / s
따라서 반발 계수 e = 충돌 후 상대 속도의 크기 충돌 전 상대 속도의 크기 = 2 m / s 4 m / s = 1 2 e = 충돌 전 상대 속도의 크기 충돌 후 상대 속도의 크기 = 4 m / s 2 m / s = 2 1
반발 계수 e e
e = 1 e = 1
0 < e < 1 0 < e < 1
e = 0 e = 0
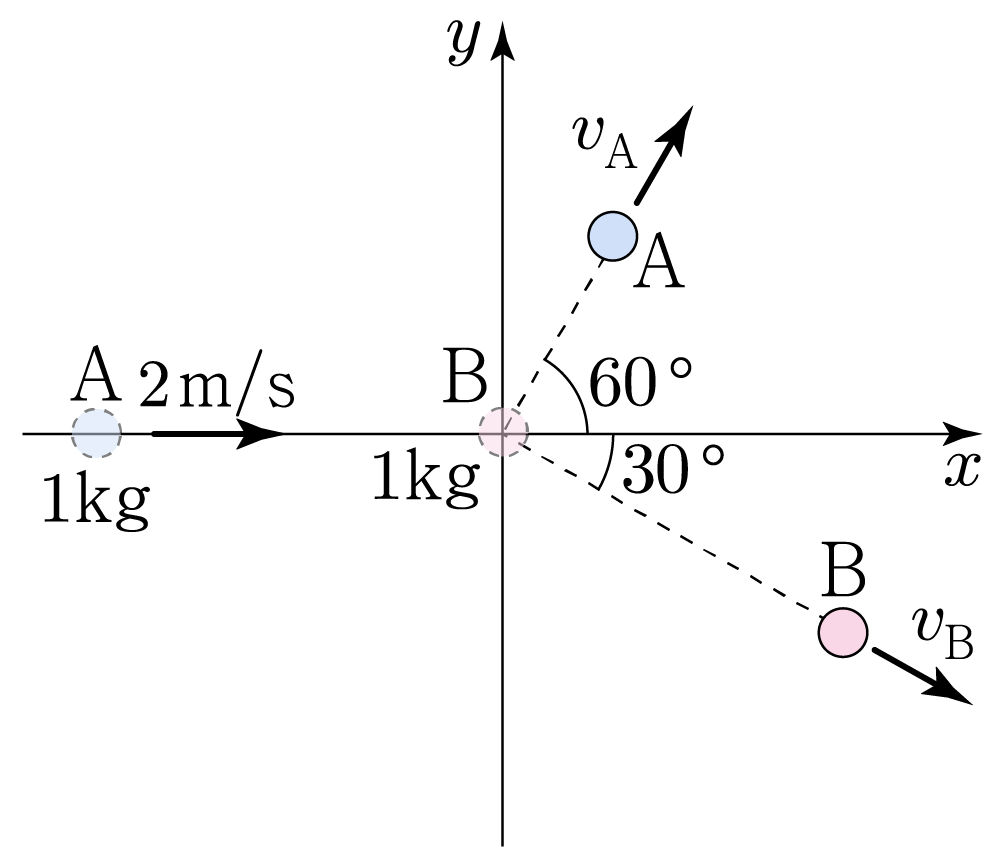
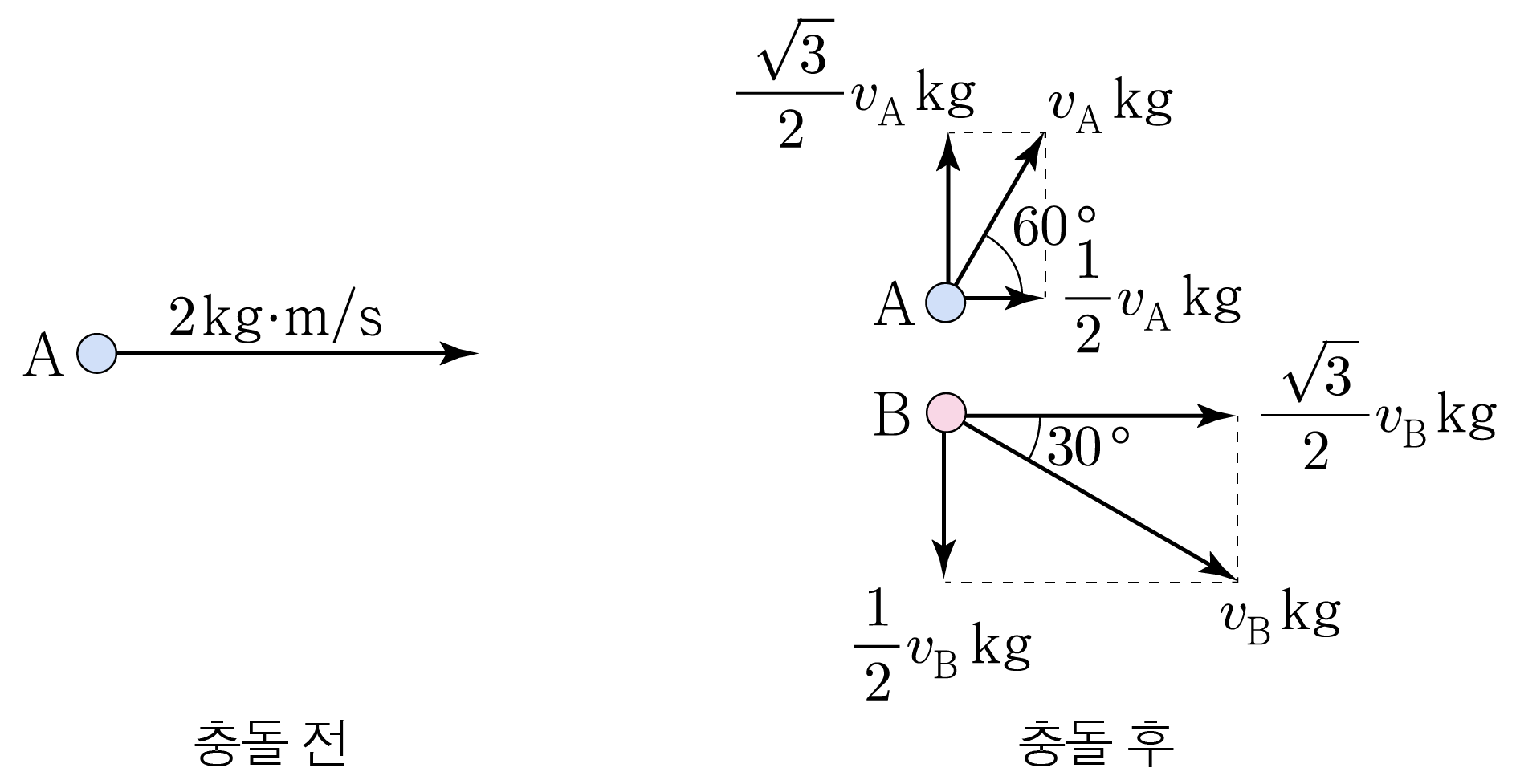
그림은 마찰이 없는 x y x y 2 m / s 2 m / s A A B B A A B B x x 6 0 ∘ 6 0 ∘ 3 0 ∘ 3 0 ∘ A A B B v A v A v B v B A A B B 1 k g 1 k g v A v A v B v B A A B B
축 방향을 양( + ) ( + ) A , B A , B x , y x , y
구분
물체
$x$ 성분
$y$ 성분
충돌 전
$\mathrm{A}$
$2\,\mathrm{kg·m/s}$
$0$
$\mathrm{B}$
$0$
$0$
충돌 후
$\mathrm{A}$
$v_{\mathrm{A}}\,\mathrm{kg} \times \cos 60^\cir$
$v_{\mathrm{A}}\,\mathrm{kg} \times \sin 60^\circ$
$\mathrm{B}$
$v_{\mathrm{B}}\,\mathrm{kg} \times \cos 30^\circ$
$-v_{\mathrm{B}}\,\mathrm{kg} \times \sin 30^\circ$
운동량 보존 법칙을 x x y y
x x 2 k g ⋅ m / s = 1 2 v A k g + 3 2 v B k g 2 k g ⋅ m / s = 2 1 v A k g + 2 3 v B k g
y y 0 = 3 2 v A k g − 1 2 v B k g , 0 = 2 3 v A k g − 2 1 v B k g , 3 2 v A k g = 1 2 v B k g , 2 3 v A k g = 2 1 v B k g , 3 2 v A = 1 2 v B , 2 3 v A = 2 1 v B , v B = 3 v A v B = 3 v A
이를 ①에 넣으면2 k g ⋅ m / s = 1 2 v A k g + 3 2 v B k g 2 k g ⋅ m / s = 2 1 v A k g + 2 3 v B k g 2 k g ⋅ m / s = 1 2 v A k g + 3 2 × 3 v A k g , 2 k g ⋅ m / s = 2 1 v A k g + 2 3 × 3 v A k g , 2 k g ⋅ m / s = 1 2 v A k g + 3 2 v A k g , 2 k g ⋅ m / s = 2 1 v A k g + 2 3 v A k g , 2 k g ⋅ m / s = 2 v A k g , 2 k g ⋅ m / s = 2 v A k g , 2 m / s = 2 v A , 2 m / s = 2 v A , v A = 1 m / s v A = 1 m / s
이를 ②에 넣으면 v B = 3 v A v B = 3 v A v B = 3 × 1 m / s , v B = 3 × 1 m / s , v B = 3 m / s v B = 3 m / s
충돌 전 A A B B 1 2 × 1 k g × ( 2 m / s ) 2 + 1 2 × 1 k g × ( 0 m / s ) 2 , 2 1 × 1 k g × ( 2 m / s ) 2 + 2 1 × 1 k g × ( 0 m / s ) 2 , 1 2 × 1 k g × ( 2 m / s ) 2 + 0 , 2 1 × 1 k g × ( 2 m / s ) 2 + 0 , 1 2 × 1 k g × 4 m 2 / s 2 , 2 1 × 1 k g × 4 m 2 / s 2 , 2 k g ⋅ m 2 / s 2 = 2 J 2 k g ⋅ m 2 / s 2 = 2 J
충돌 후 A A B B 1 2 × 1 k g × ( 1 m / s ) 2 + 1 2 × 1 k g × ( 3 m / s ) 2 , 2 1 × 1 k g × ( 1 m / s ) 2 + 2 1 × 1 k g × ( 3 m / s ) 2 , 1 2 × 1 k g × 1 m 2 / s 2 + 1 2 × 1 k g × 3 m 2 / s 2 , 2 1 × 1 k g × 1 m 2 / s 2 + 2 1 × 1 k g × 3 m 2 / s 2 , 2 k g ⋅ m 2 / s 2 = 2 J 2 k g ⋅ m 2 / s 2 = 2 J
충돌 전후 물체의 운동 에너지의 합이 같으므로 A A B B
1번 문항 정답 및 해설 보기
정답: $4$
ㄱ. A A B B
ㄴ. 오른쪽 방향을 양( + ) ( + ) A A B B 4 k g × 7 m / s + M × ( − 3 m / s ) , 4 k g × 7 m / s + M × ( − 3 m / s ) , 28 k g ⋅ m / s − 3 M k g ⋅ m / s 2 8 k g ⋅ m / s − 3 M k g ⋅ m / s
충돌 후 A A B B ( 4 k g + M ) × 1 m / s , ( 4 k g + M ) × 1 m / s , ( 4 k g + M ) k g ⋅ m / s ( 4 k g + M ) k g ⋅ m / s
충돌하는 물체의 운동량의 합은 운동량 보존 법칙에 의해 충돌 전과 후가 같으므로28 k g ⋅ m / s − 3 M k g ⋅ m / s = ( 4 k g + M ) k g ⋅ m / s , 2 8 k g ⋅ m / s − 3 M k g ⋅ m / s = ( 4 k g + M ) k g ⋅ m / s , 28 k g ⋅ m / s − 3 M k g ⋅ m / s = 4 k g ⋅ m / s + M k g ⋅ m / s , 2 8 k g ⋅ m / s − 3 M k g ⋅ m / s = 4 k g ⋅ m / s + M k g ⋅ m / s , 24 k g ⋅ m / s = 4 M k g ⋅ m / s , 2 4 k g ⋅ m / s = 4 M k g ⋅ m / s , M = 6 k g M = 6 k g
ㄷ. 충돌 전 A A B B 1 2 × 4 k g × ( 7 m / s ) 2 + 1 2 × 6 k g × ( 3 m / s ) 2 , 2 1 × 4 k g × ( 7 m / s ) 2 + 2 1 × 6 k g × ( 3 m / s ) 2 , 1 2 × 4 k g × 49 m 2 / s 2 + 1 2 × 6 k g × 9 m 2 / s 2 , 2 1 × 4 k g × 4 9 m 2 / s 2 + 2 1 × 6 k g × 9 m 2 / s 2 , 98 k g ⋅ m 2 / s 2 + 27 k g ⋅ m 2 / s 2 , 9 8 k g ⋅ m 2 / s 2 + 2 7 k g ⋅ m 2 / s 2 , 125 k g ⋅ m 2 / s 2 = 125 J 1 2 5 k g ⋅ m 2 / s 2 = 1 2 5 J
충돌 후 A A B B 1 2 × ( 4 k g + 6 k g ) × ( 1 m / s ) 2 , 2 1 × ( 4 k g + 6 k g ) × ( 1 m / s ) 2 , 1 2 × 10 k g × 1 m 2 / s 2 , 2 1 × 1 0 k g × 1 m 2 / s 2 , 5 k g ⋅ m 2 / s 2 = 5 J 5 k g ⋅ m 2 / s 2 = 5 J
그러므로 A A B B 125 J − 5 J = 120 J 1 2 5 J − 5 J = 1 2 0 J
따라서 정답은 4 4
2번 문항 정답 및 해설 보기
정답: $5$
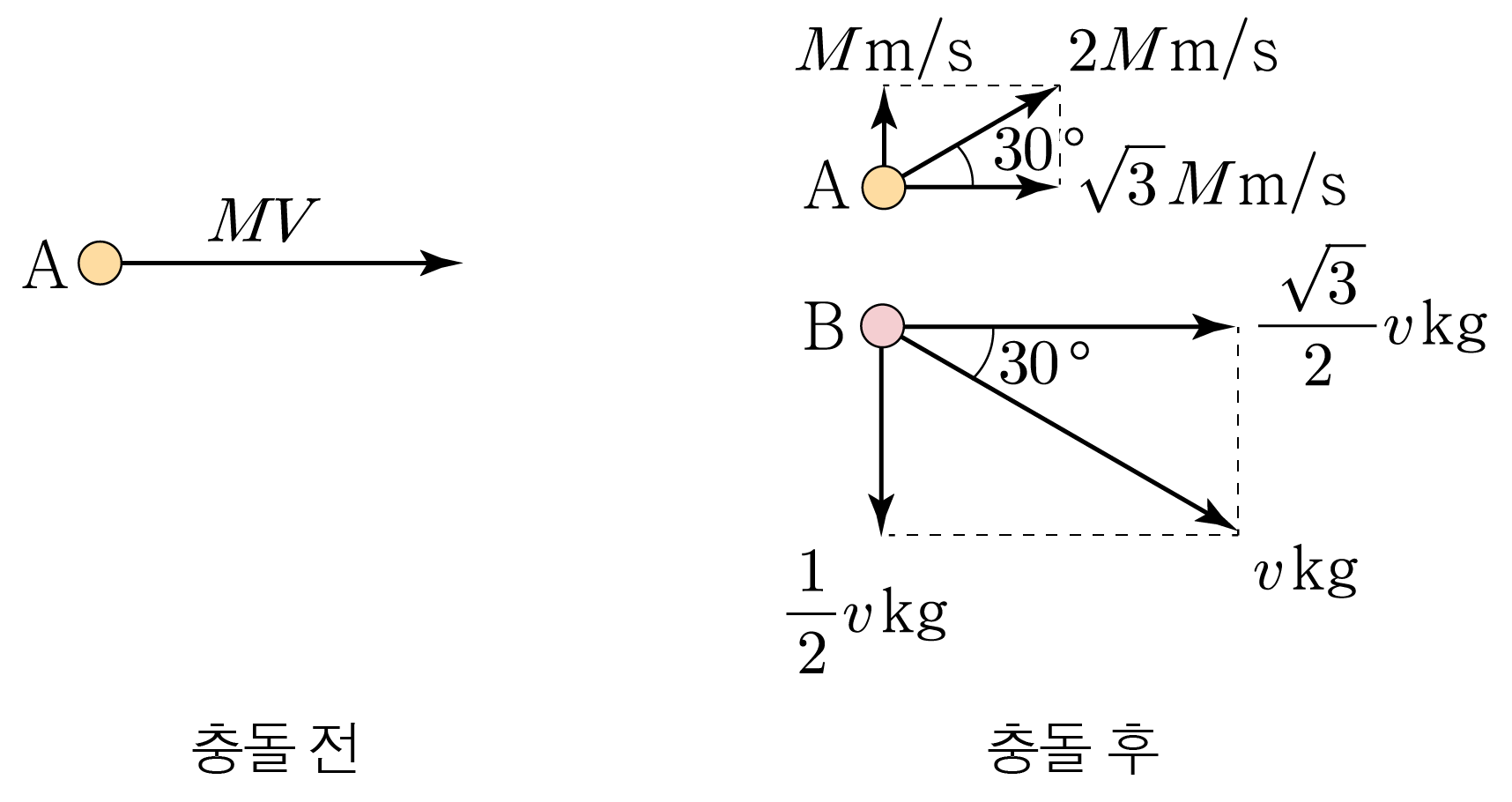
ㄱ. 축 방향을 양( + ) ( + ) A , B A , B x , y x , y
구분
물체
$x$ 성분
$y$ 성분
충돌 전
$\mathrm{A}$
$MV$
$0$
$\mathrm{B}$
$0$
$0$
충돌 후
$\mathrm{A}$
$2M\,\mathrm{m/s} \times \cos 30^\circ$
$2M\,\mathrm{m/s} \times \sin 30^\circ$
$\mathrm{B}$
$v\,\mathrm{kg} \times \cos 30^\circ$
$-v\,\mathrm{kg} \times \sin 30^\circ$
운동량 보존 법칙을 x x y y
x x M V = 3 M m / s + 3 2 v k g M V = 3 M m / s + 2 3 v k g
y y 0 = M m / s − 1 2 v k g , 0 = M m / s − 2 1 v k g , M m / s = 1 2 v k g , M m / s = 2 1 v k g , M = 1 2 v k g ⋅ s / m M = 2 1 v k g ⋅ s / m
이를 ①에 넣으면M V = 3 M m / s + 3 2 v k g M V = 3 M m / s + 2 3 v k g 1 2 v k g ⋅ s / m × V = 3 × 1 2 v k g + 3 2 v k g , 2 1 v k g ⋅ s / m × V = 3 × 2 1 v k g + 2 3 v k g , 1 2 v s / m × V = 3 × 1 2 v + 3 2 v , 2 1 v s / m × V = 3 × 2 1 v + 2 3 v , v 2 s / m × V = 3 2 v + 3 2 v , 2 v s / m × V = 2 3 v + 2 3 v , 1 2 s / m × V = 3 2 + 3 2 , 2 1 s / m × V = 2 3 + 2 3 , V 2 s / m = 3 v , 2 V s / m = 3 v , V s / m = 2 3 , V s / m = 2 3 , V = 2 3 m / s V = 2 3 m / s
ㄴ. 충돌 전 A A B B 1 2 × M × ( 2 3 m / s ) 2 + 1 2 × 1 k g × ( 0 ) 2 , 2 1 × M × ( 2 3 m / s ) 2 + 2 1 × 1 k g × ( 0 ) 2 , 1 2 × M × ( 2 3 m / s ) 2 + 0 , 2 1 × M × ( 2 3 m / s ) 2 + 0 , 1 2 × M × 12 m 2 / s 2 , 2 1 × M × 1 2 m 2 / s 2 , 6 M m 2 / s 2 6 M m 2 / s 2
충돌 후 A A B B 1 2 × M × ( 2 m / s ) 2 + 1 2 × 1 k g × v 2 , 2 1 × M × ( 2 m / s ) 2 + 2 1 × 1 k g × v 2 , 1 2 × M × 4 m 2 / s 2 + 1 2 × 1 k g × v 2 , 2 1 × M × 4 m 2 / s 2 + 2 1 × 1 k g × v 2 , 2 M m 2 / s 2 + 1 2 v 2 k g 2 M m 2 / s 2 + 2 1 v 2 k g
탄성 충돌을 하므로 충돌 전후 A A B B 6 M m 2 / s 2 = 2 M m 2 / s 2 + 1 2 v 2 k g , 6 M m 2 / s 2 = 2 M m 2 / s 2 + 2 1 v 2 k g , 4 M m 2 / s 2 = 1 2 v 2 k g , 4 M m 2 / s 2 = 2 1 v 2 k g , M m 2 / s 2 = 1 8 v 2 k g , M m 2 / s 2 = 8 1 v 2 k g , M = 1 8 v 2 k g ⋅ s 2 / m 2 M = 8 1 v 2 k g ⋅ s 2 / m 2
이를 ②에 넣으면M = 1 2 v k g ⋅ s / m M = 2 1 v k g ⋅ s / m 1 8 v 2 k g ⋅ s 2 / m 2 = 1 2 v k g ⋅ s / m , 8 1 v 2 k g ⋅ s 2 / m 2 = 2 1 v k g ⋅ s / m , 1 8 v 2 s / m = 1 2 v , 8 1 v 2 s / m = 2 1 v , 1 8 v s / m = 1 2 , 8 1 v s / m = 2 1 , 1 4 v s / m = 1 , 4 1 v s / m = 1 , v = 4 m / s v = 4 m / s
ㄷ. v = 4 m / s v = 4 m / s M = 1 2 v k g ⋅ s / m M = 2 1 v k g ⋅ s / m M = 2 k g M = 2 k g
따라서 정답은 5 5
