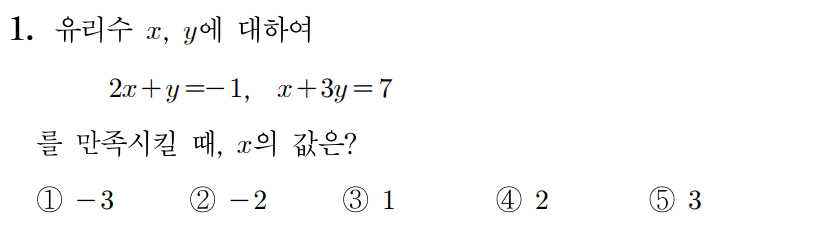값을 모르는 수이다. 수학에서 미지수는 보통 x,y,z 등으로 나타낸다.
미지수와 숫자 사이의 곱셈 기호는 생략할 수 있다.
곱셈 기호를 생략할 때 숫자는 미지수의 왼쪽 바로 옆에 적으며, 미지수의 계수라 한다.
예를 들어, x×5는 5x와 같고, x의 계수는 5이다.
(x+2)×4와 같이 괄호 안에 미지수가 있고 괄호 밖에 곱하는 수가 있을 때, ‘괄호 밖에 곱하는 수’를 ‘괄호 안의 식의 각 항’에 곱한 후 더하여 계산한다.
예를 들어, (x+2)×4를 계산할 때, 4를 괄호 안의 식 (x+2)의 각 항인 x와 2에 곱한 후 더해 (x×4)+(2×4)=4x+8과 같이 계산할 수 있다.
미지수가 포함된 식이다. 방정식을 풀어 미지수의 값을 찾을 수 있다.
(x+5)×2=14 방정식을 풀어 미지수 x를 구해보자.
(x+5)×2=14,
(x×2)+(5×2)=14,
2x+10=14,
2x=4,
x=2이다.
2개 이상의 미지수를 포함하는 방정식들의 묶음이다. 연립 방정식은 대입법과 소거법(가감법)을 통해 풀 수 있다.
-
대입법
하나의 방정식에서 미지수 하나에 관련된 값을 구한 후 다른 방정식에 대입하여 푸는 방법이다.
-
소거법(가감법)
미지수의 계수를 맞춘 후, 두 방정식을 더하거나 빼 미지수를 제거하여 푸는 방법이다.
2개의 방정식 x+y=8,2x+3y=21을 통해 x와 y 값을 구해보자.
-
대입법으로 풀기
x+y=8에서 x=8−y이므로 이를 2x+3y=21에 대입한다.
2x+3y=21,
2×(8−y)+3y=21,
(16−2y)+3y=21,
16−2y+3y=21,
16+y=21,
y=5이다.
이를 x+y=8 또는 2x+3y=21에 대입하여
x=3임을 알 수 있다.
-
소거법(가감법)으로 풀기
x+y=8의 양변에 2를 곱해 2x+3y=21과 x의 계수를 맞춘다.
(x+y)×2=8×2,
2x+2y=16이다.
2x+2y=16에서 2x+3y=21을 빼 x를 제거한다.
2x+2y−(2x+3y)=16−21,
2x+2y−2x−3y=−5,
2y−3y=−5,
−y=−5,
y=5이다.
이를 x+y=8 또는 2x+3y=21에 대입하여
x=3임을 알 수 있다.
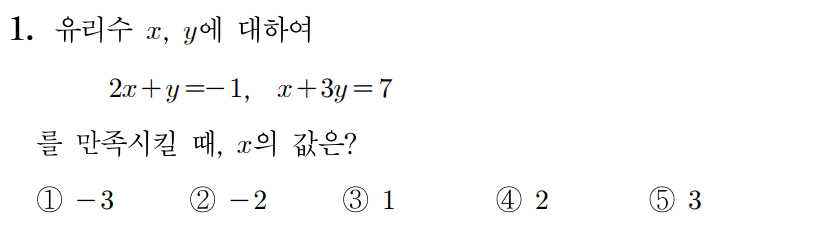
정답: $2$
-
대입법으로 풀기
2x+y=−1에서 y=−1−2x이므로 이를 x+3y=7에 대입한다.
x+3y=7,
x+3×(−1−2x)=7,
x−3−6x=7,
−3−5x=7,
−5x=10,
x=−2이다.
-
소거법(가감법)으로 풀기
2x+y=−1의 양변에 3을 곱해 x+3y=7과 y의 계수를 맞춘다.
(2x+y)×3=−1×3,
6x+3y=−3이다.
6x+3y=−3에서 x+3y=7을 빼 y를 제거한다.
6x+3y−(x+3y)=−3−7,
6x+3y−x−3y=−10,
5x=−10,
x=−2이다.
따라서 정답은 2번이다.

정답: $3$
-
대입법으로 풀기
x+y+z=6에서 x=6−y−z이므로 이를 2x+y+z=7, 3x+2y+z=10에 각각 대입한다.
2x+y+z=7에 대입하면
2×(6−y−z)+y+z=7,
12−2y−2z+y+z=7,
12−y−z=7,
−y−z=−5,
y+z=5이다.
3x+2y+z=10에 대입하면
3×(6−y−z)+2y+z=10,
18−3y−3z+2y+z=10,
18−y−2z=10,
−y−2z=−8,
y+2z=8이다.
y+z=5에서 y=5−z이므로 이를 y+2z=8에 대입한다.
y+2z=8,
(5−z)+2z=8,
5−z+2z=8,
5+z=8,
z=3이다.
-
소거법(가감법)으로 풀기
x+y+z=6과 2x+y+z=7은 y,z의 계수가 이미 맞춰져 있으므로 바로 x+y+z=6에서 2x+y+z=7을 빼 y,z를 제거한다.
x+y+z−(2x+y+z)=6−7,
x+y+z−2x−y−z=6−7,
−x=−1,
x=1이다.
이를 x+y+z=6과 3x+2y+z=10에 대입한다.
x+y+z=6에 대입하면
x+y+z=6,
1+y+z=6,
y+z=5이다.
3x+2y+z=10에 대입하면
3x+2y+z=10,
3+2y+z=10,
2y+z=7이다.
y+z=5의 양변에 2를 곱해 2y+z=7과 y의 계수를 맞춘다.
(y+z)×2=5×2,
2y+2z=10이다.
2y+2z=10에서 2y+z=7을 빼 y를 제거하면
2y+2z−(2y+z)=10−7,
2y+2z−2y−z=10−7,
z=3이다.
따라서 정답은 3번이다.