¶ 지식 정보
¶ 파동
어느 지점에서 발생한 진동이 전달되는 현상이다.
¶ 매질
파동을 전달해 주는 물질이다.
매질이 제자리에서 진동하여 파동을 전달한다.

¶ 파동의 종류
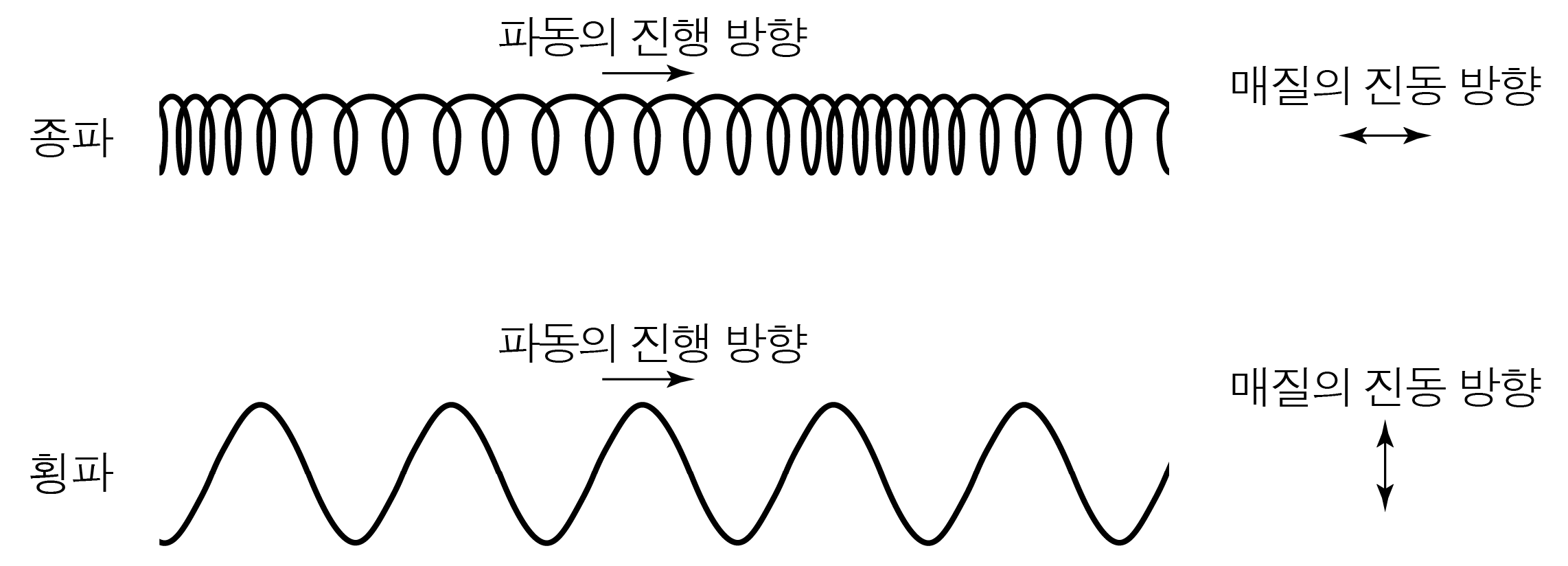
파동의 진행 방향과 매질의 진동 방향의 관계에 따라 종파와 횡파로 나눌 수 있다.
-
종파: 파동의 진행 방향과 매질의 진동 방향이 나란한 파동
종파 예시: 소리 -
횡파: 파동의 진행 방향과 매질의 진동 방향이 수직인 파동
횡파 예시: 빛
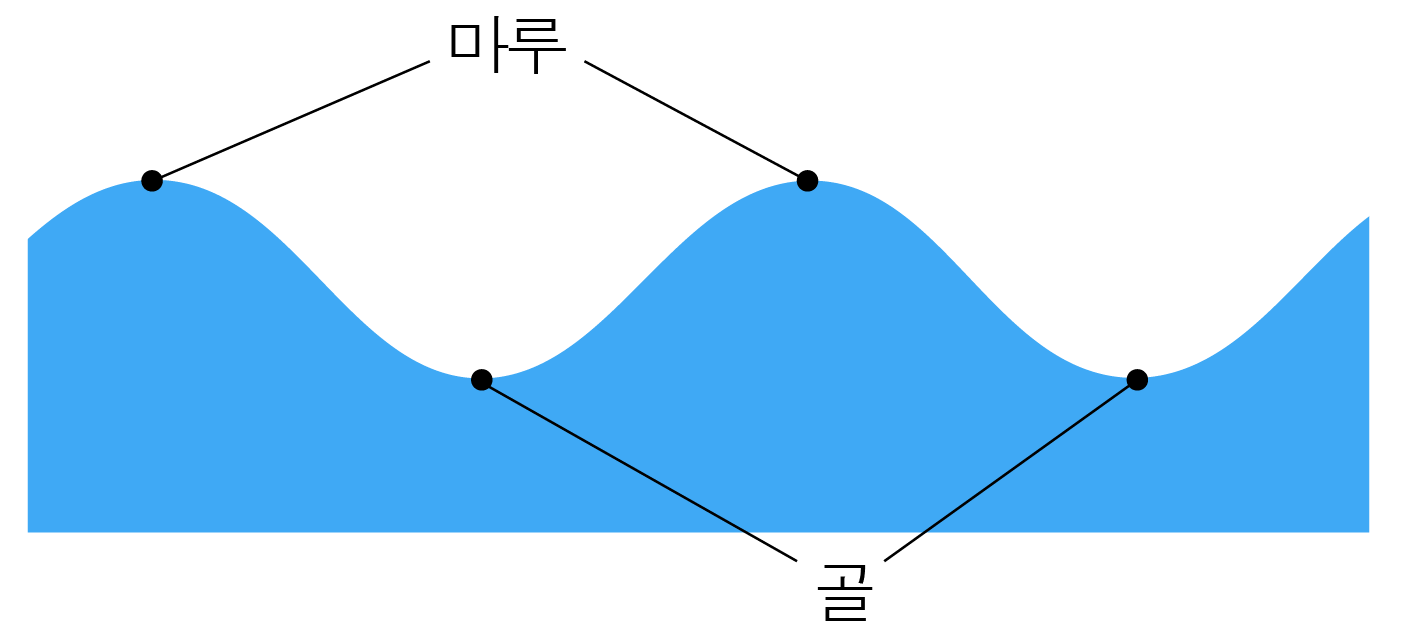
¶ 마루와 골
파동에서 가장 높은 부분을 마루, 가장 낮은 부분을 골이라 한다.
¶ 마루와 골 예시
다음은 시간 일 때, 파동의 변위 를 위치 에 따라 나타낸 것이다.
이 파동의 마루와 골의 위치를 구해보자. (단, 축의 단위는 이다.)
를 그리면 아래 그림과 같다.
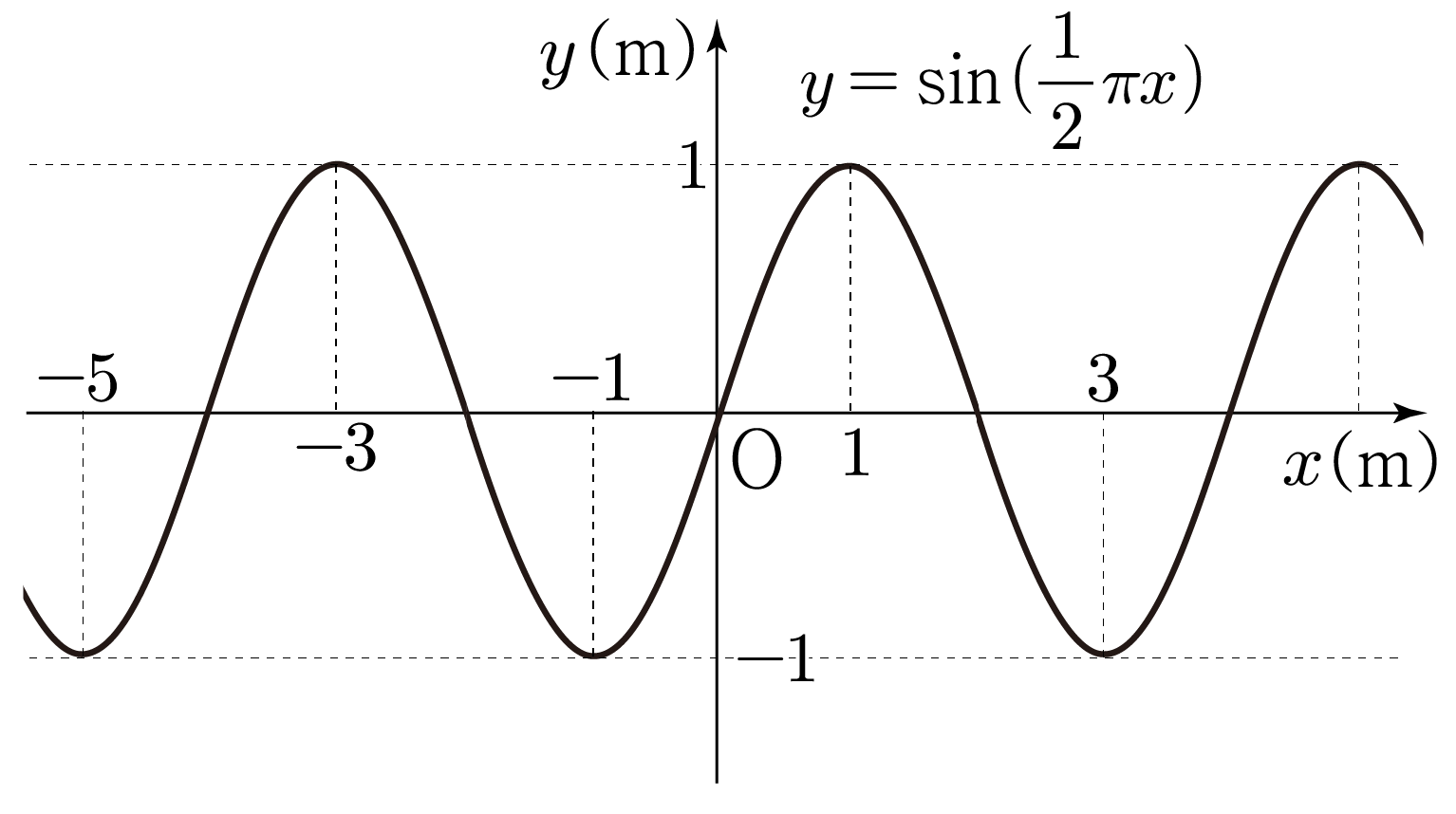
일 때, 로 가장 크므로 마루에 해당하며,
일 때, 로 가장 작으므로 골에 해당한다.
¶ 파동의 표현
파동은 파장, 진폭, 주기, 진동수, 위상을 통해 표현한다.
¶ 파장
인접한 마루와 마루 또는 골과 골 사이의 거리이다.
기본 단위는 이고, 기호로는 로 나타낸다.
¶ 파장 예시
다음은 시간 일 때, 파동의 변위 를 위치 에 따라 나타낸 것이다.
이 파동의 파장을 구해보자. (단, 축의 단위는 이다.)
를 그리면 아래 그림과 같다.
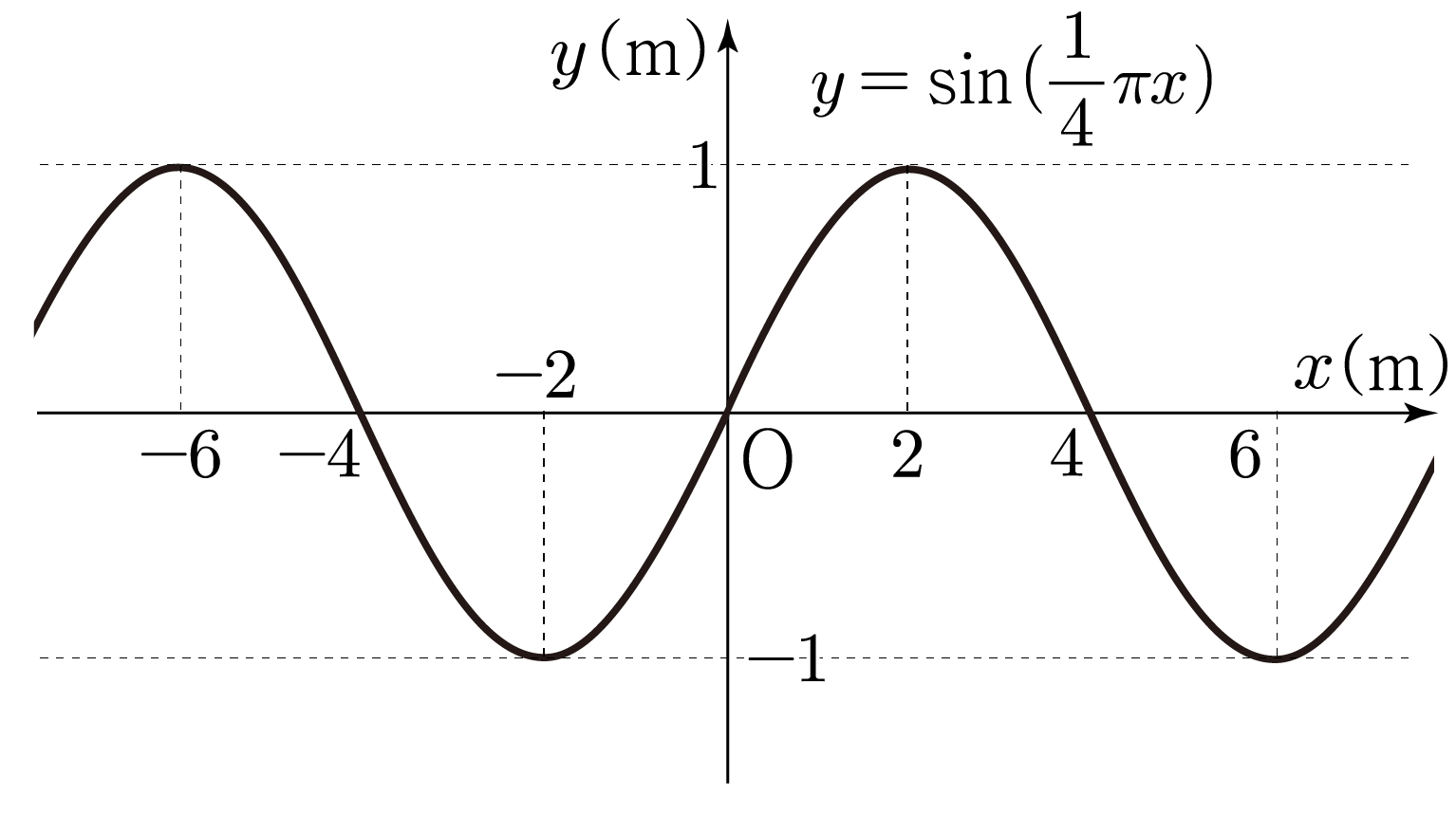
인접한 마루와 마루 사이의 거리로 파장 구하기:
일 때, 가 가장 큰 값을 가져 마루에 해당하므로 인접한 마루와 마루 사이의 거리는 이다.
인접한 골과 골 사이의 거리로 파장 구하기:
일 때, 가 가장 작은 값을 가져 골에 해당하므로 인접한 골과 골 사이의 거리는 이다.
¶ 진폭
매질의 진동 중심으로부터 마루 또는 골까지의 수직 거리이다.
기본 단위는 이고, 기호로는 로 나타낸다.
¶ 진폭 예시
다음은 시간 일 때, 파동의 변위 를 위치 에 따라 나타낸 것이다.
이 파동의 진폭을 구해보자. (단, 축의 단위는 이다.)
를 그리면 아래 그림과 같다.
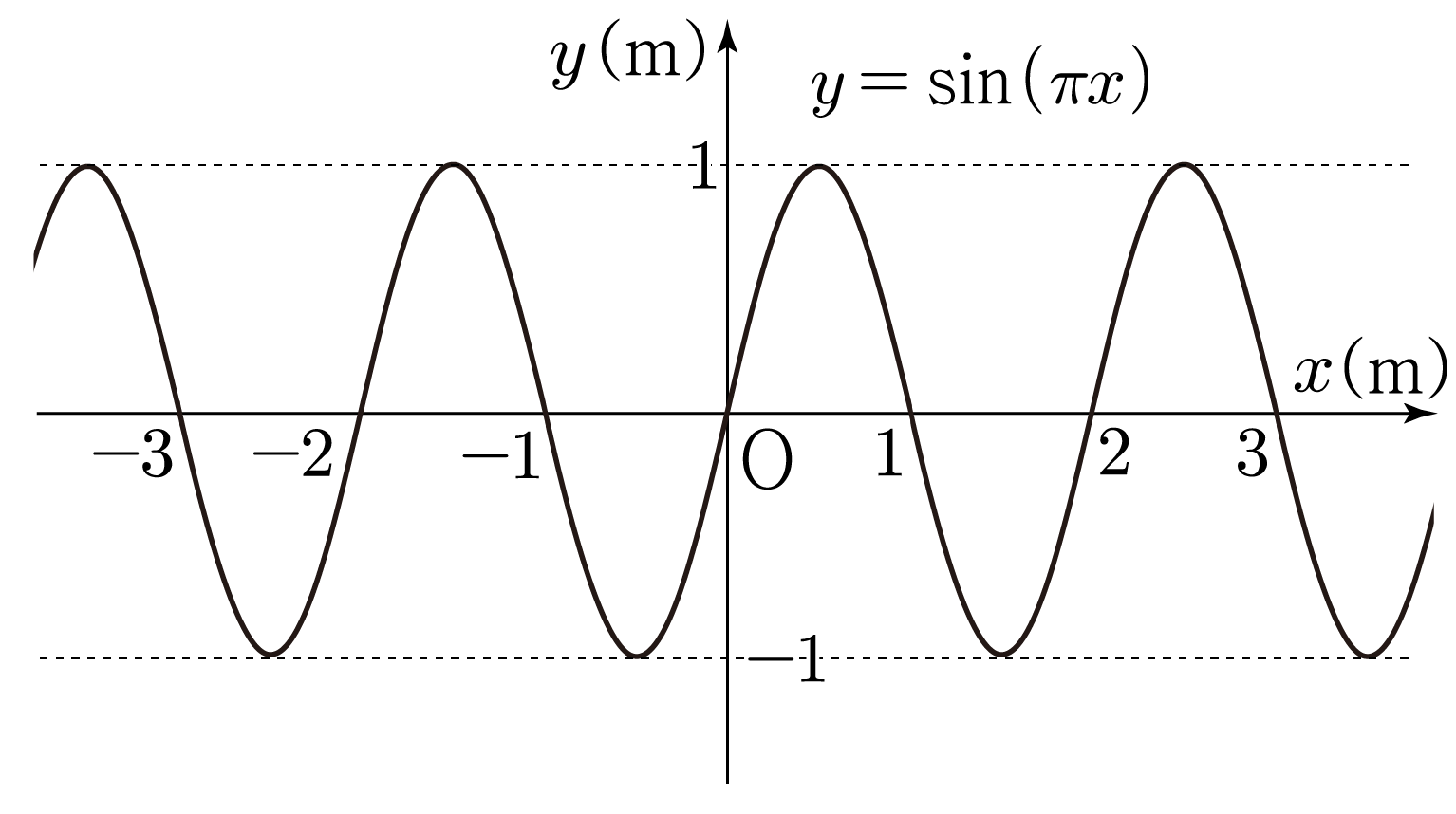
의 진동 중심 으로부터 마루 또는 골까지의 수직 거리는 이므로 진폭은 이다.
¶ 주기
매질의 한 점이 한 번 진동하는데 걸리는 시간이다.
매질의 한 점이 마루가 된 순간부터 다음 마루가 되는 때까지 걸린 시간과 같고, 기본 단위는 이며, 기호로는 로 나타낸다.
¶ 진동수
주기의 역수인 값이다.
기본 단위는 또는 (와 같은 의미)이고, 기호로는 로 나타낸다.
진동수는 주기의 역수이므로 수식으로 나타내면 이다.
주기와 진동수는 매질이 달라져도 변하지 않고 일정하다.
¶ 주기와 진동수 예시
그림 (가)는 시간 일 때, 어느 물결파가 진행하는 것을 나타낸 것이고, (나)는 점 의 변위를 에 따라 나타낸 것이다.
물결파의 주기와 진동수를 구해보자.
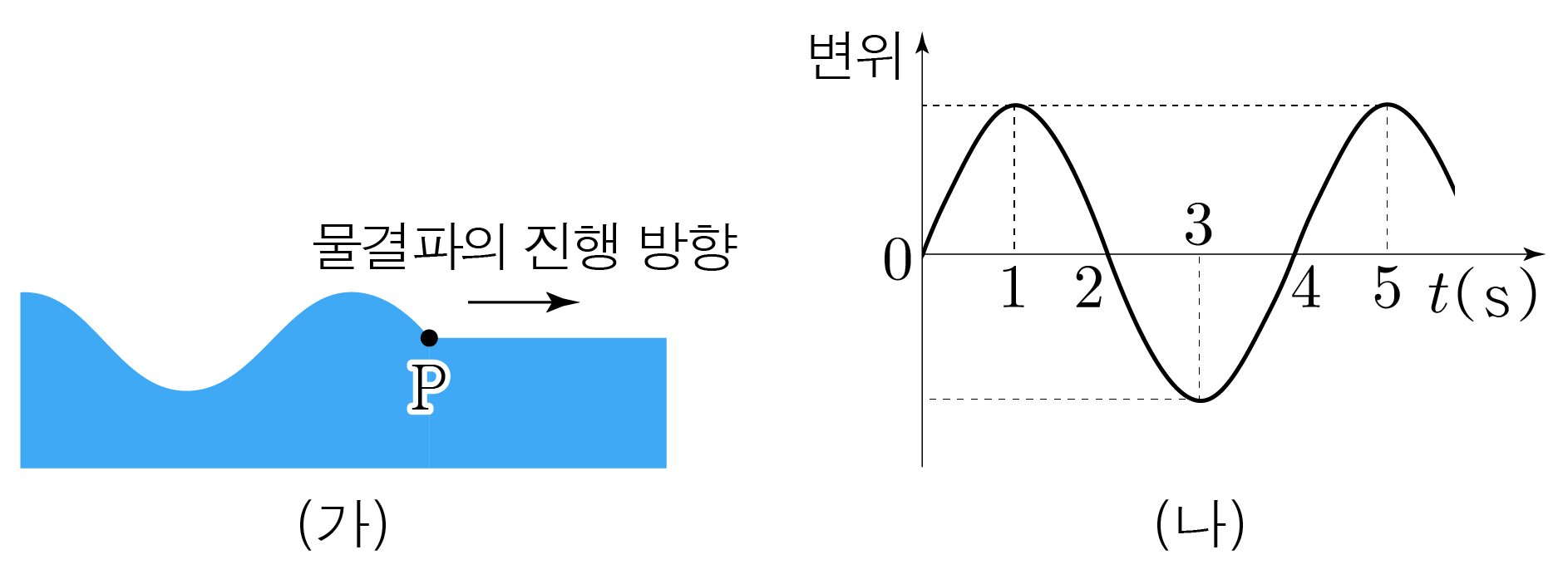
(나)에서 매질의 한 점 가 마루가 된 순간부터 다음 마루가 되는 때까지 걸린 시간은 이므로 주기는 이다.
진동수는 주기의 역수이므로 진동수는 이다.
¶ 위상
파동의 한 파장에서 어느 위치에 있는지를 나타낸 각도이다.
기본 단위는 이고, 기호로는 로 나타낸다.
¶ 위상 예시
그림은 시간 일 때, 어느 파동의 변위를 위치에 따라 나타낸 것이다.
점 중 점 와 위상이 같은 점은 어디인지 구해보자.
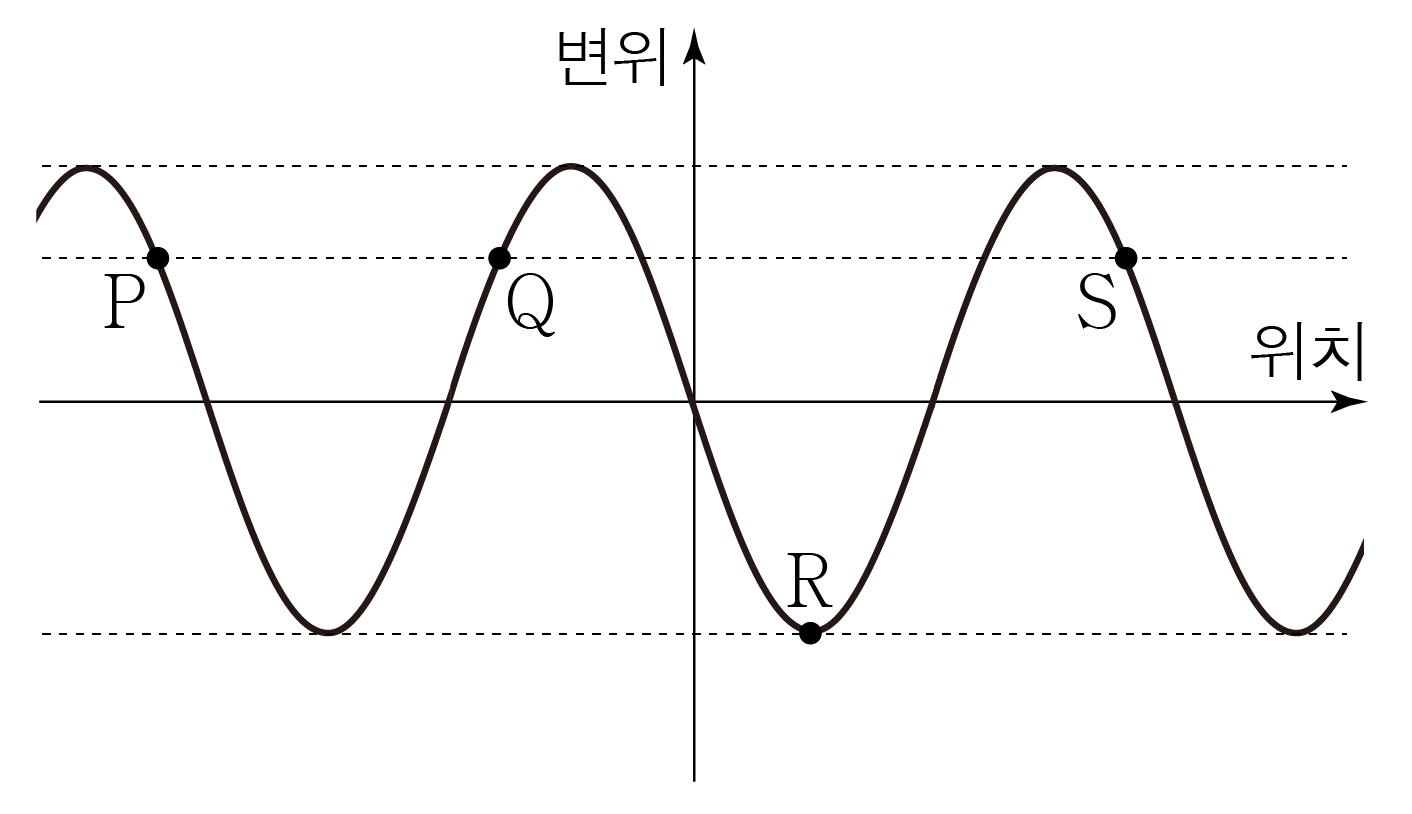
아래 그림에서 부터 까지를 한 파장이라 할 때,
위상은 그라데이션(한 파장) 내에서의 위치에 해당하므로 놓여 있는 위치의 그라데이션 색상이 같은 경우 위상이 같다.
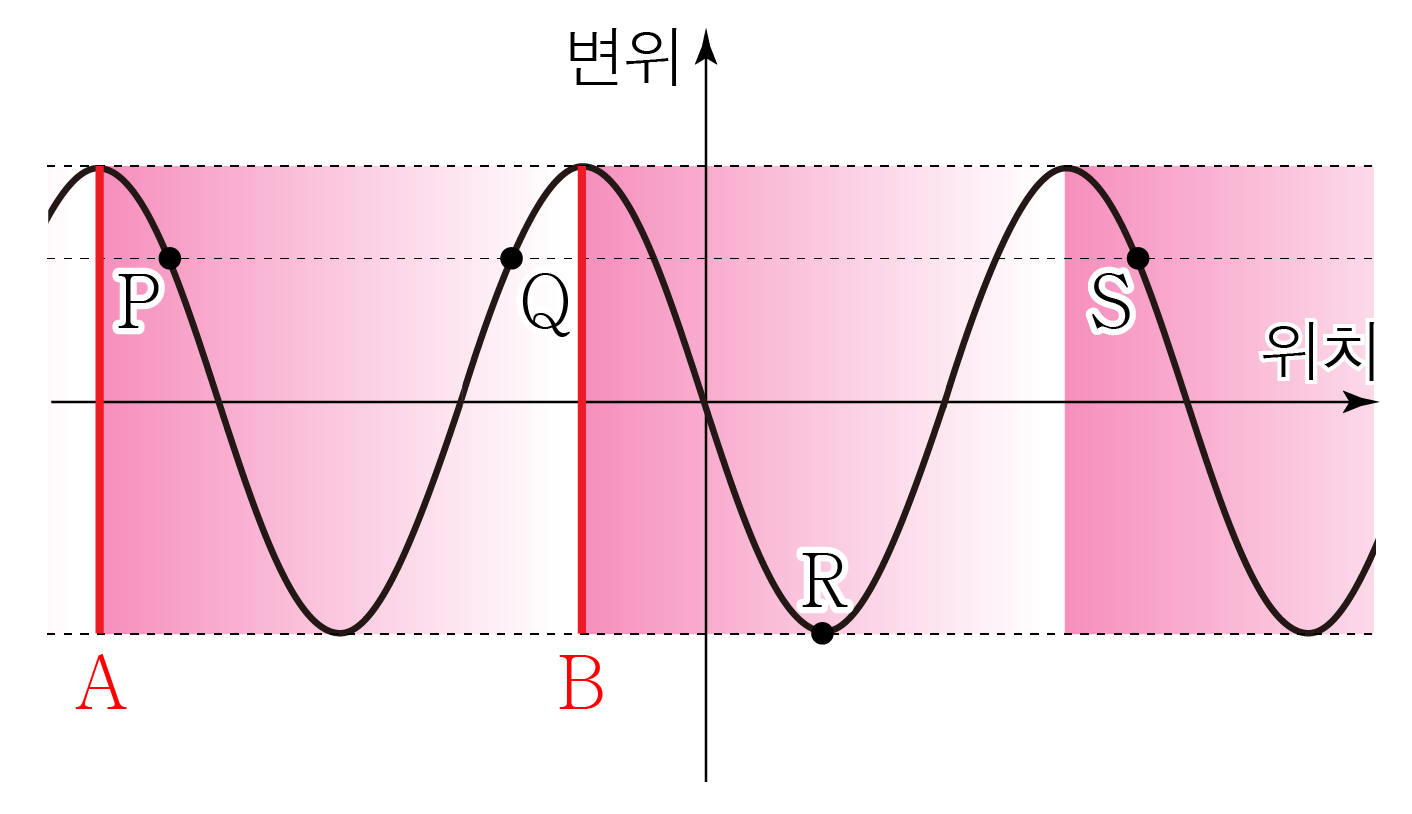
따라서 중 와 위상이 같은 점은 이다.
¶ 적용 문항
¶ 1번 문항
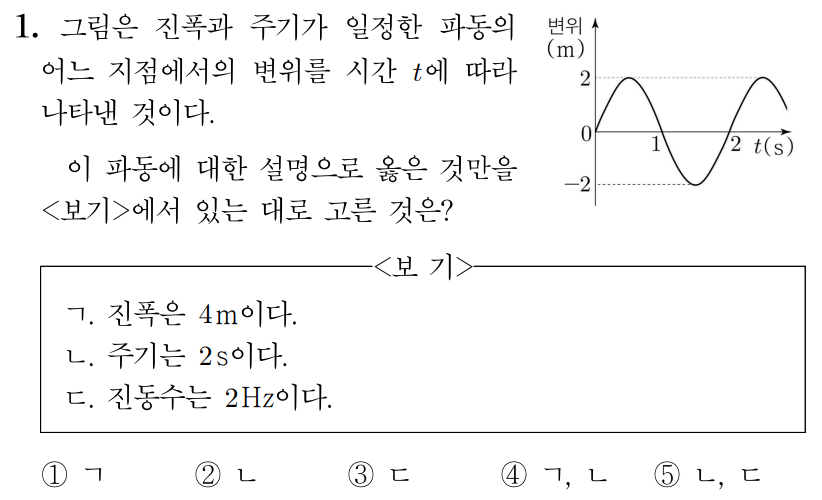
정답: $2$
ㄱ. 진폭은 매질의 진동 중심(변위가 인 지점)으로부터 마루 또는 골까지의 수직 거리이므로 파동의 진폭은 이다. (X)
ㄴ. 주기는 매질의 한 점이 한 번 진동하는데 걸리는 시간이므로 파동의 주기는 이다. (O)
ㄷ. 진동수는 주기의 역수인 값이므로 이다. (X)
따라서 정답은 번이다.
¶ 2번 문항
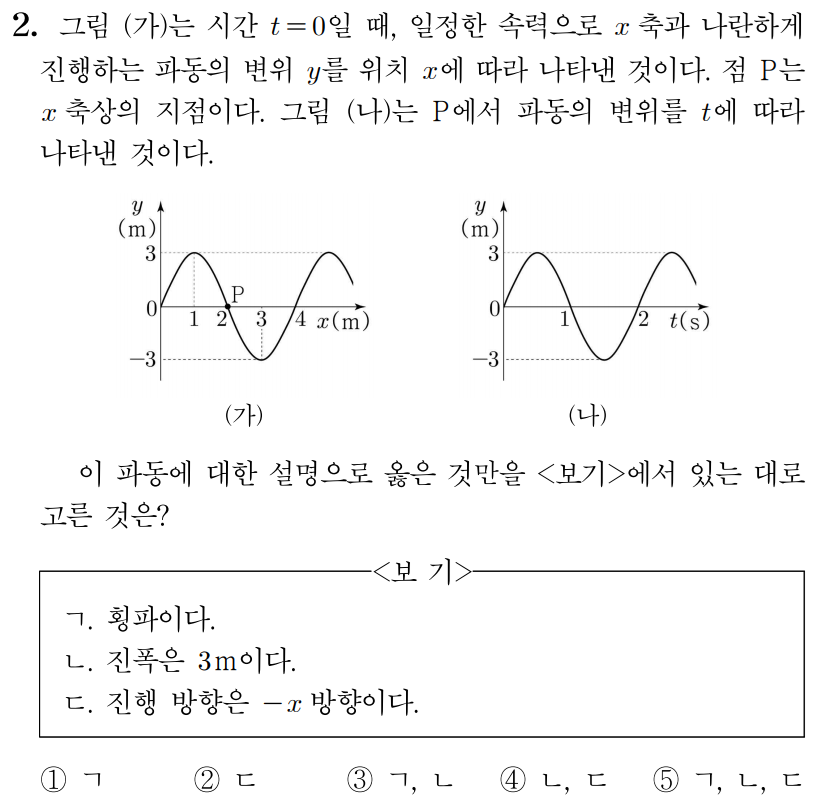
정답: $3$
ㄱ. 파동은 축과 나란하게 진행하며, (나)를 통해 매질의 진동 방향은 축과 나란함을 알 수 있다.
그러므로 파동의 진행 방향과 매질의 진동 방향이 수직인 횡파이다. (O)
ㄴ. 진폭은 매질의 진동 중심(변위가 인 지점)으로부터 마루 또는 골까지의 수직 거리이므로 파동의 진폭은 이다. (O)
ㄷ. 직후 에서의 변위는 증가하므로 (가)에서 파동은 방향으로 진행함을 알 수 있다.
그러므로 파동의 진행 방향은 방향이다. (X)
따라서 정답은 번이다.






