sin,cos,tan 등으로 이루어진 함수이다.
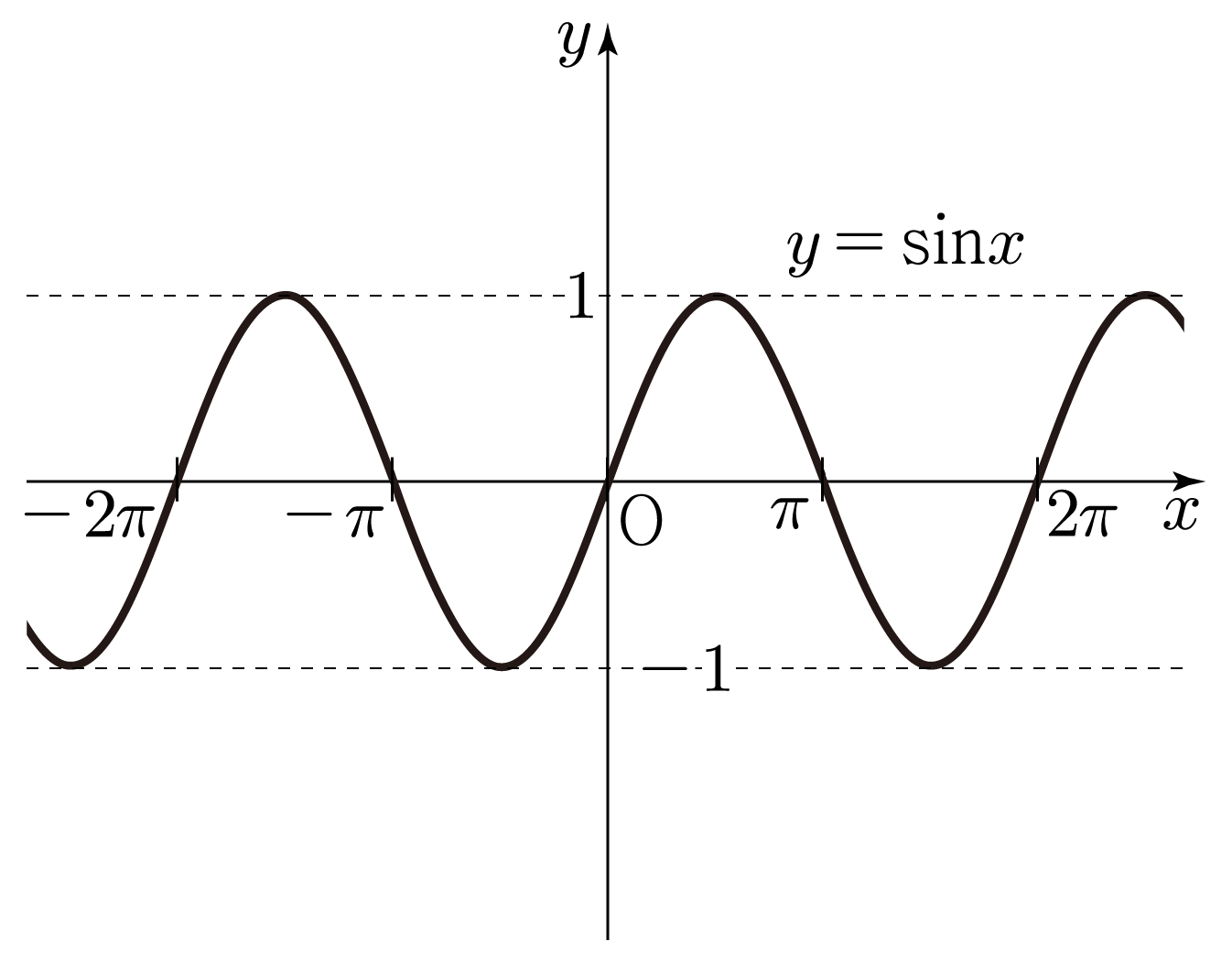
y=sinx의 그래프는 아래와 같다.
- y는 최댓값 1과 최솟값 −1을 갖는다.
- 물결 모양이 2π를 주기로 반복되며 x=0일 때, y=0이다.
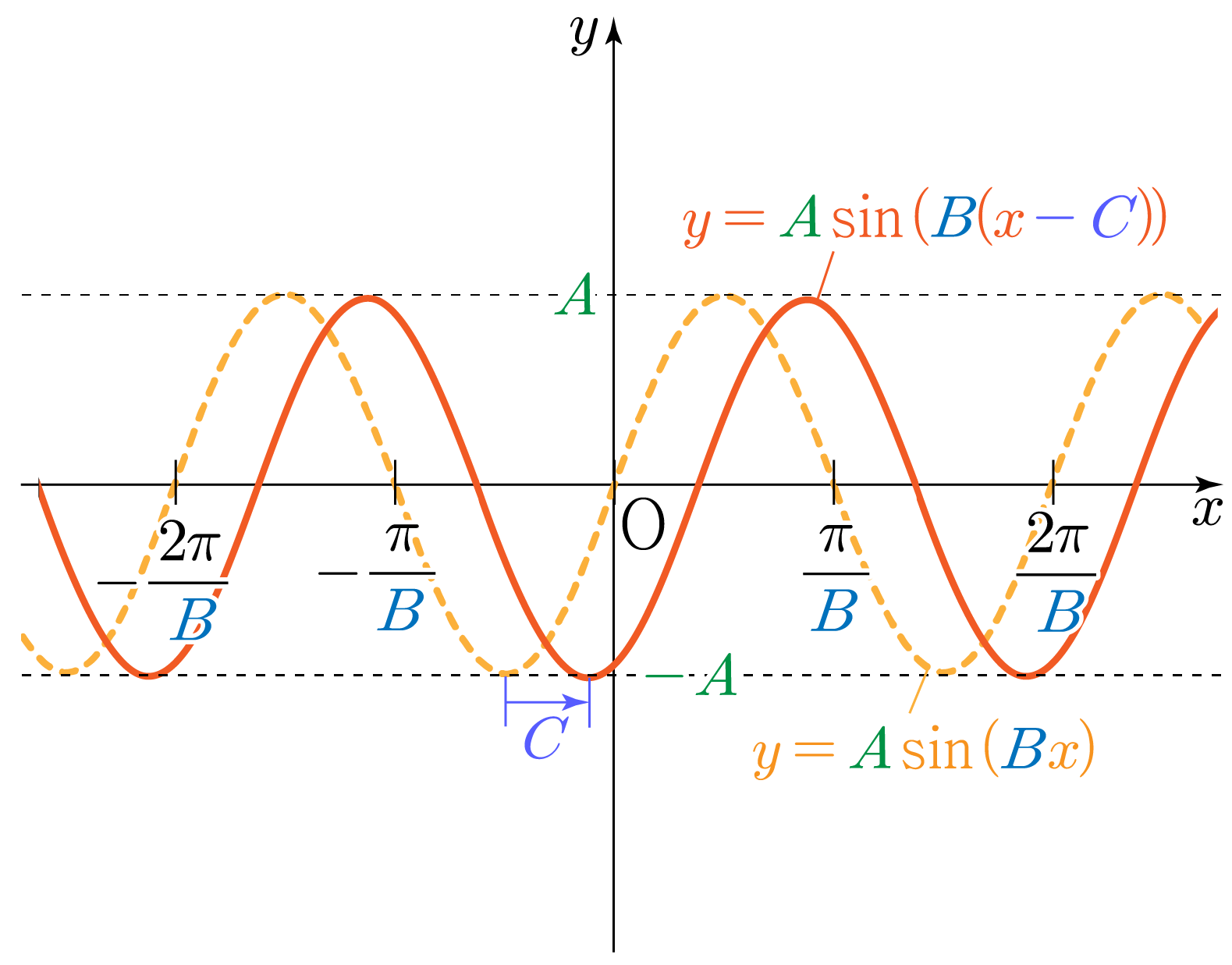
y=Asin(B(x−C))의 그래프는 아래와 같다.
- y는 최댓값 A와 최솟값 −A를 갖는다.
- 물결 모양이 B2π를 주기로 반복된다.
- y=Asin(Bx)의 그래프를 x축 방향으로 C만큼 움직인 형태이다.
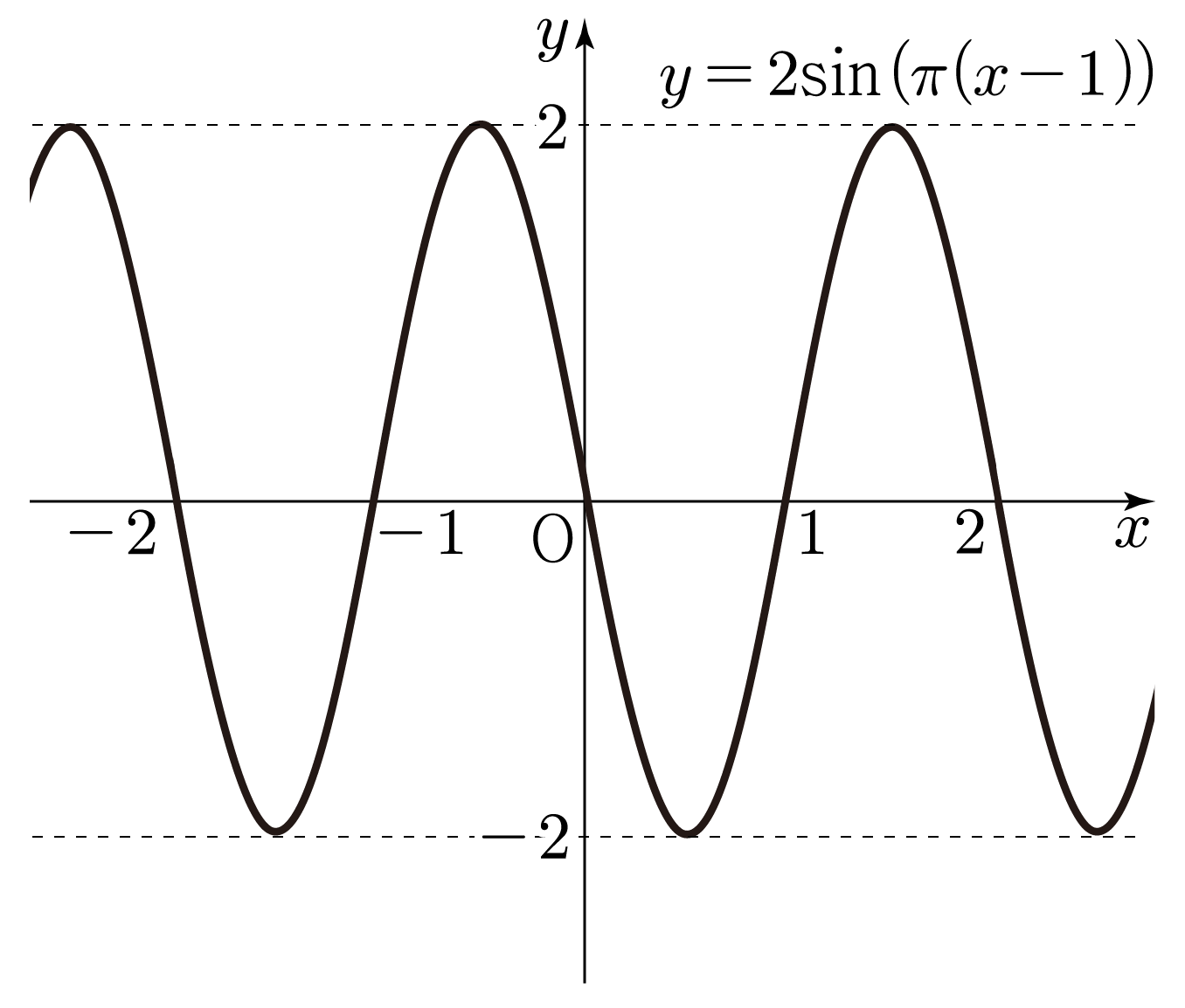
y=2sin(π(x−1))의 그래프를 그려보자.
y=Asin(B(x−C))에서 A=2,B=π,C=1이므로
- y는 최댓값 2와 최솟값 −2를 갖는다.
- 물결 모양이 π2π=2를 주기로 반복된다.
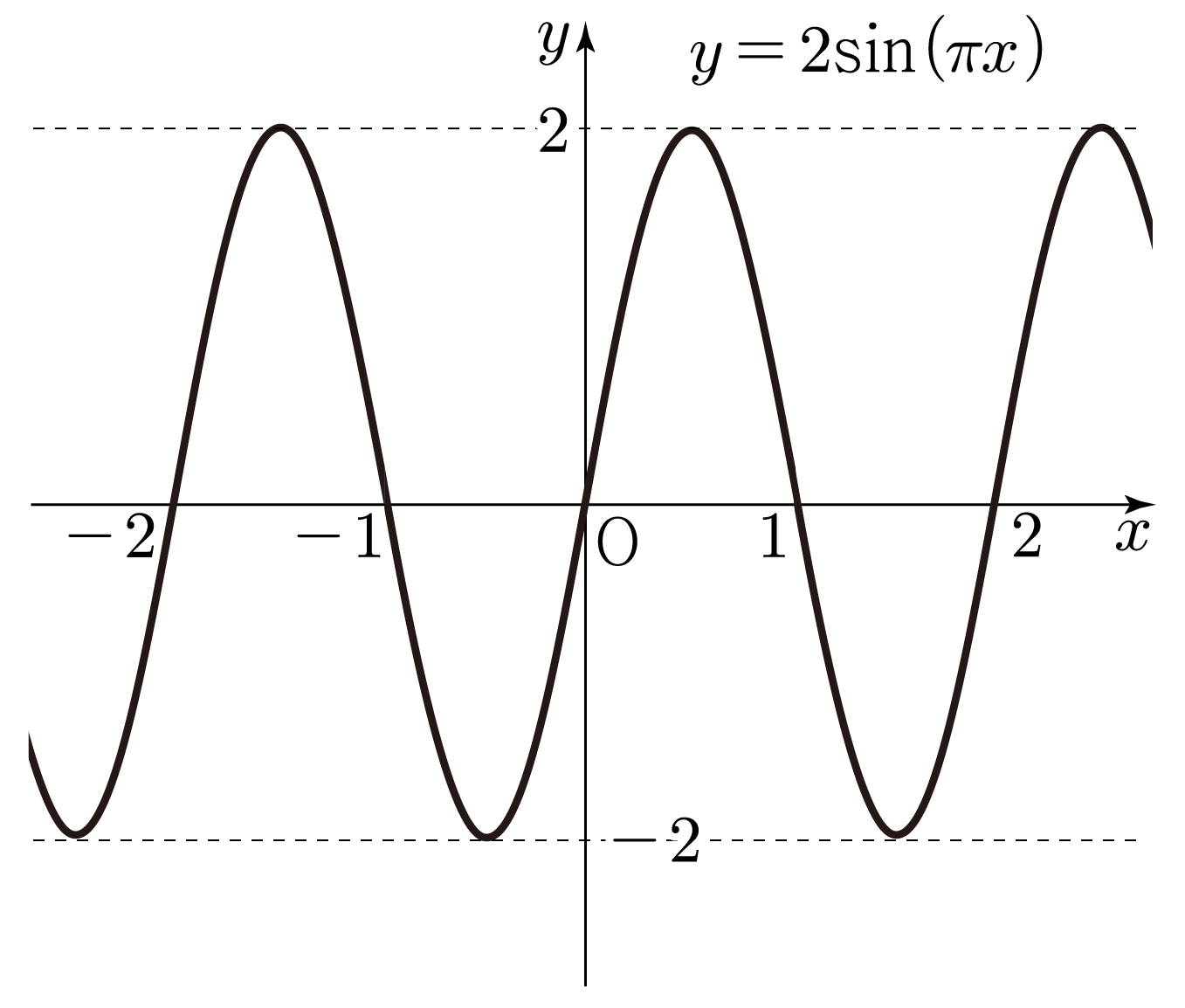
- 아래의 y=2sin(πx)의 그래프를 x축 방향으로 1만큼 움직인 형태이다.
따라서 y=2sin(π(x−1))의 그래프를 그리면 아래와 같다.
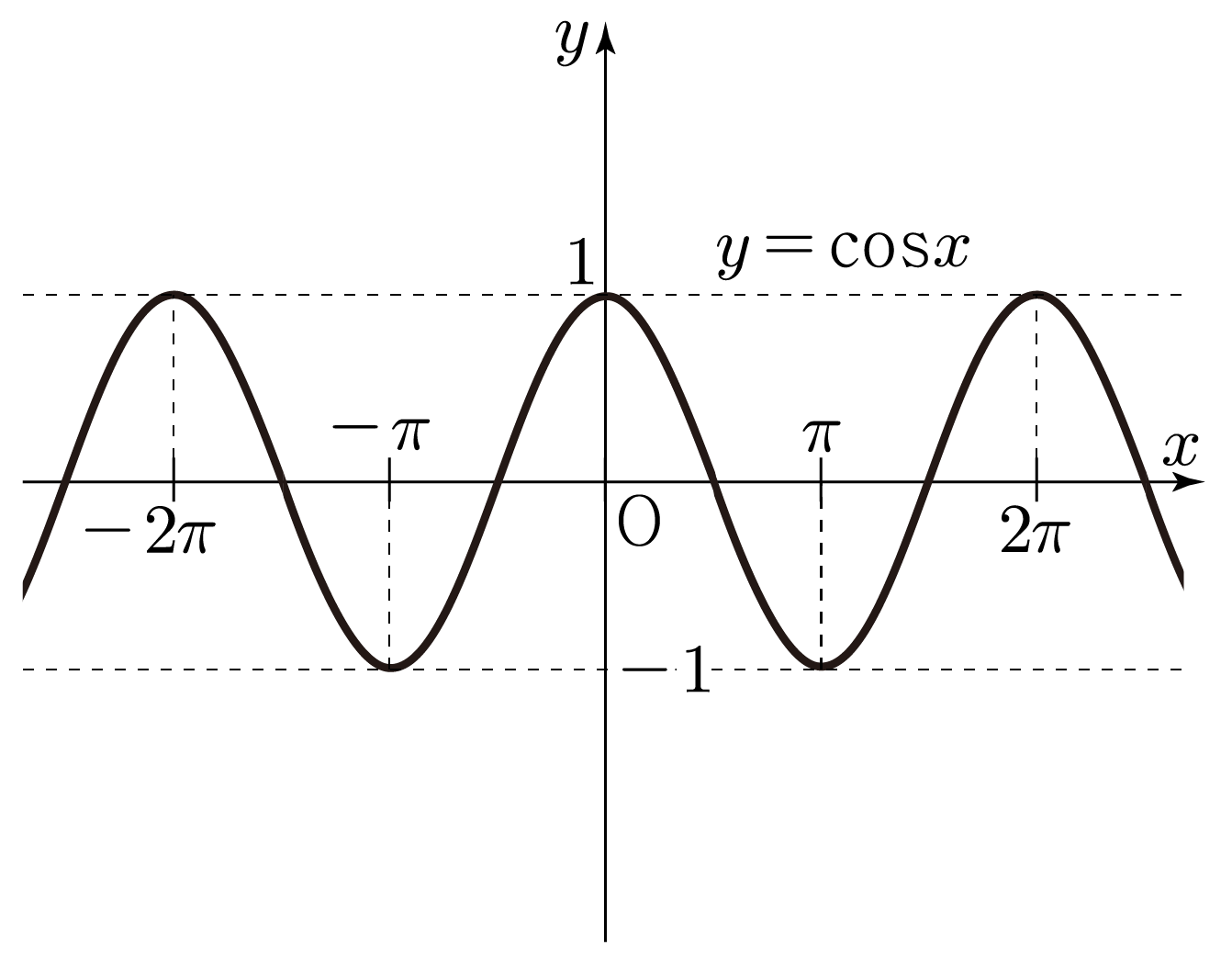
y=cosx의 그래프는 아래와 같다.
- y는 최댓값 1과 최솟값 −1을 갖는다.
- 물결 모양이 2π를 주기로 반복되며 x=0일 때, y는 최댓값 1이다.
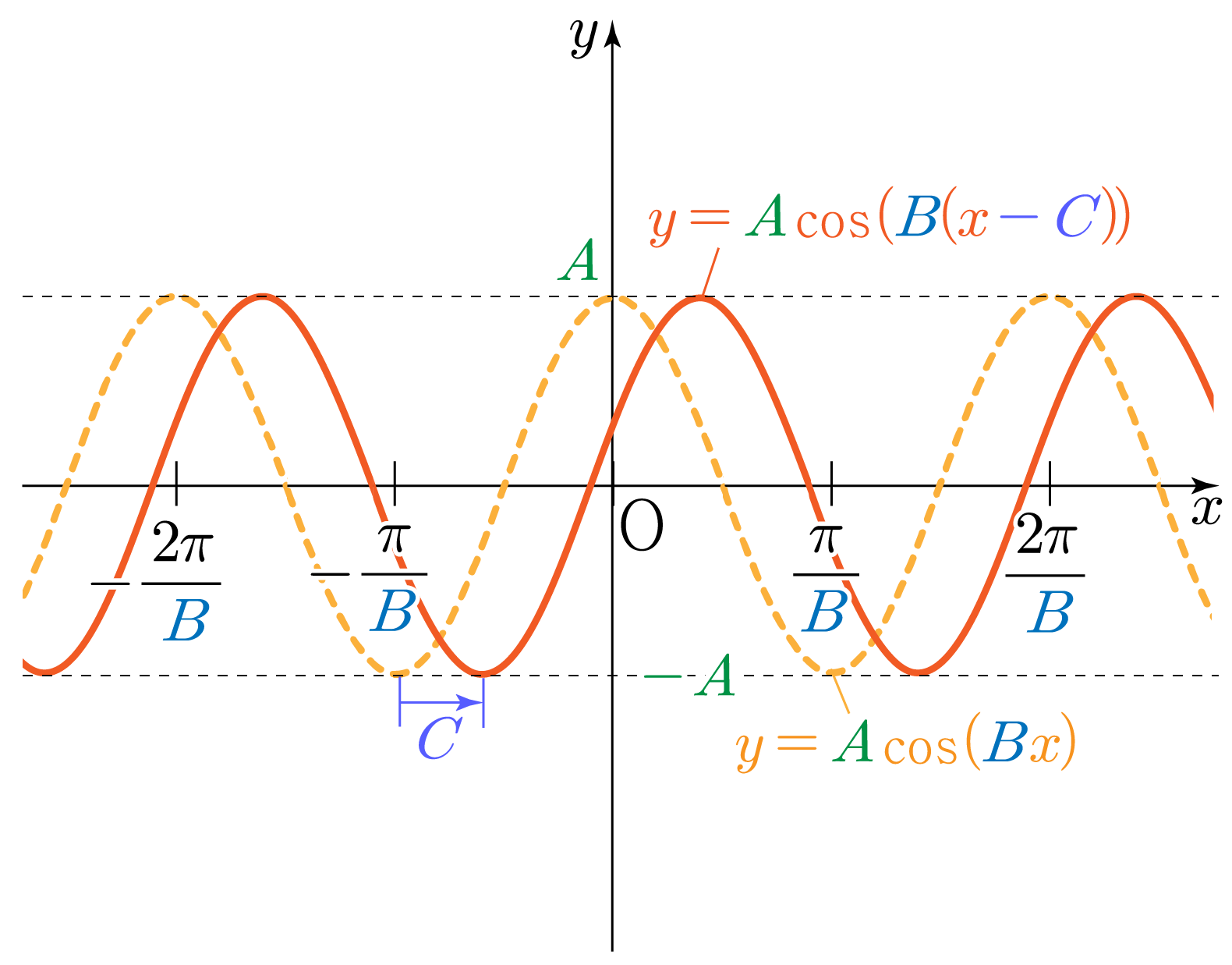
y=Acos(B(x−C))의 그래프는 아래와 같다.
- y는 최댓값 A와 최솟값 −A를 갖는다.
- 물결 모양이 B2π를 주기로 반복된다.
- y=Acos(Bx)의 그래프를 x축 방향으로 C만큼 움직인 형태이다.
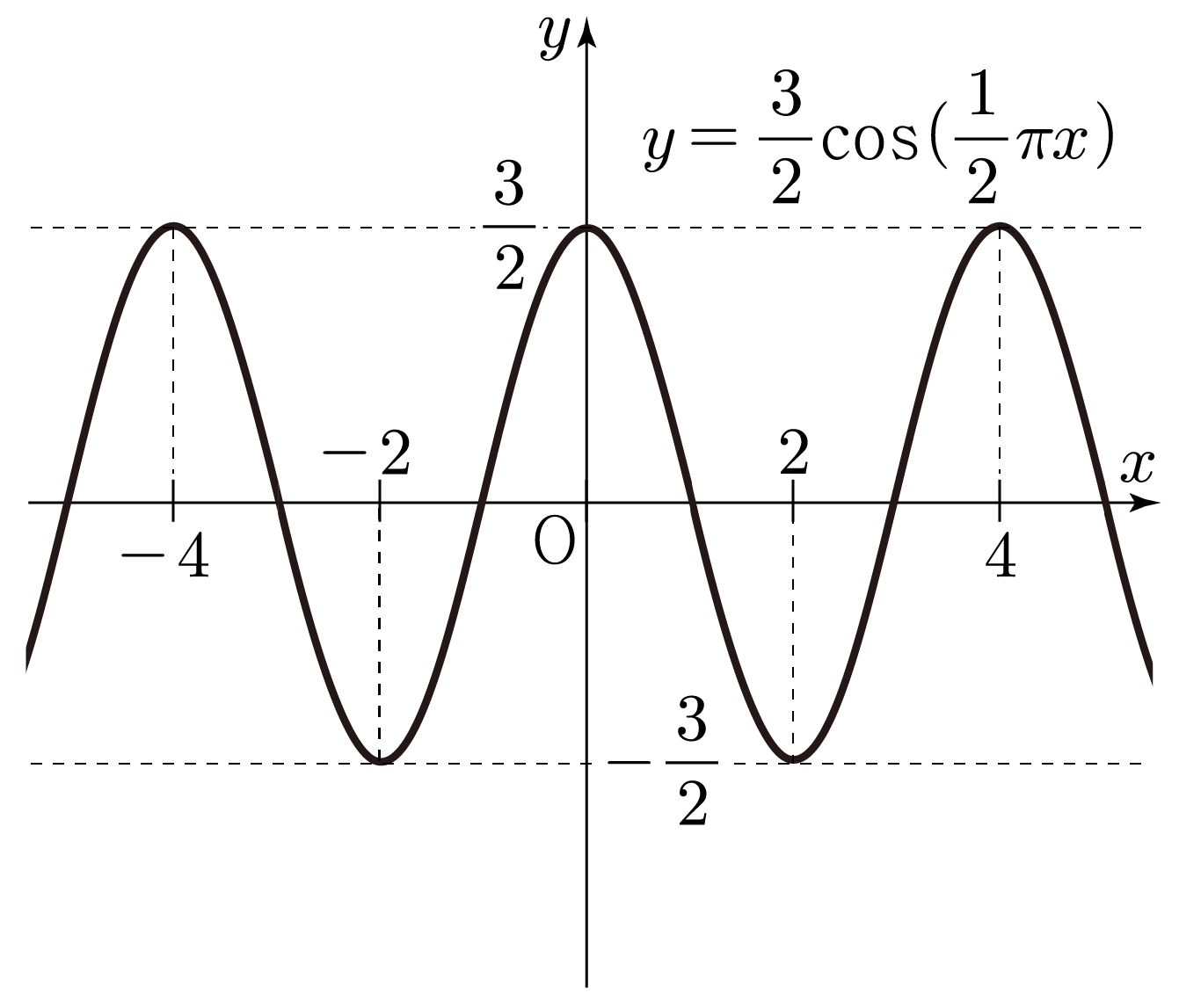
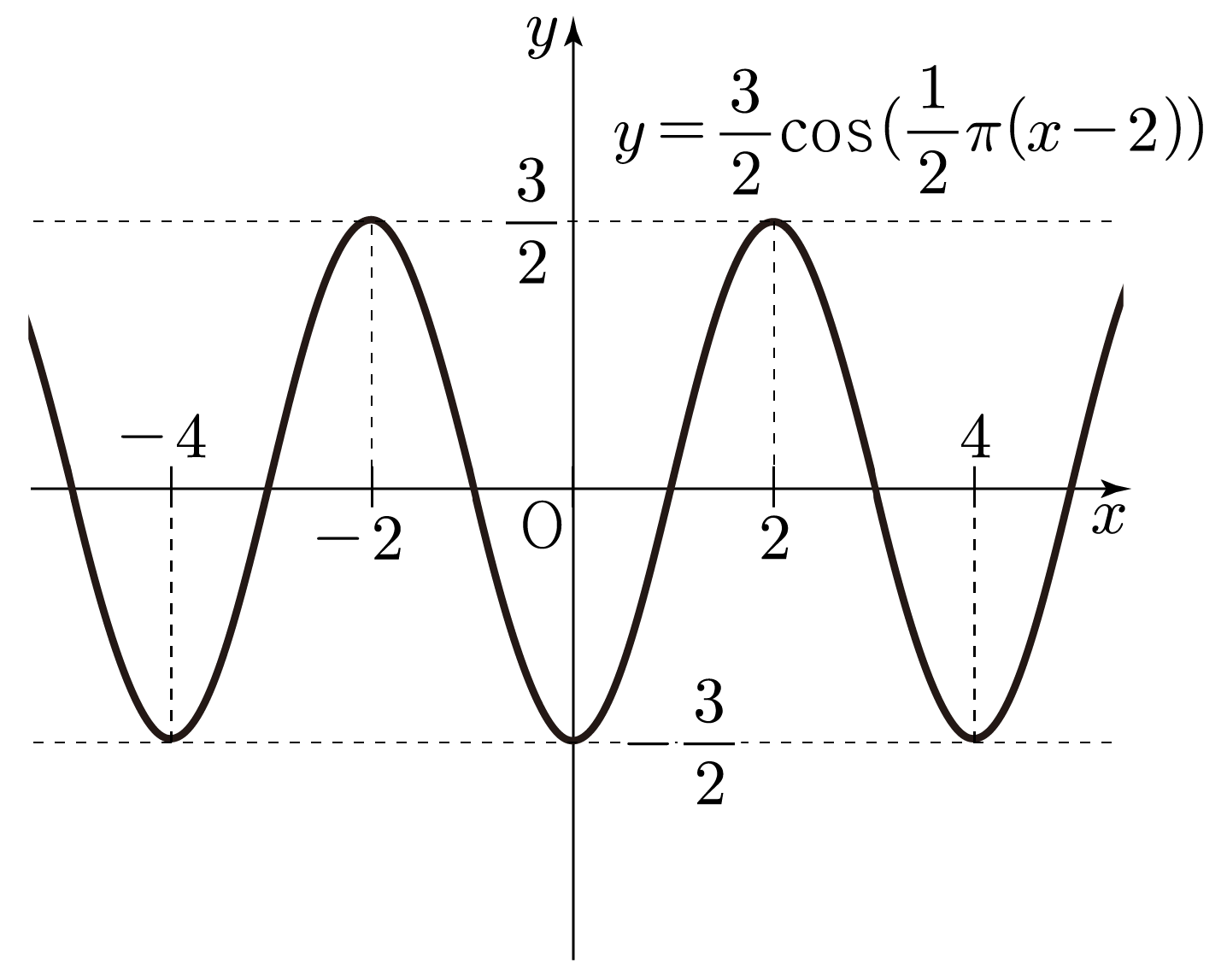
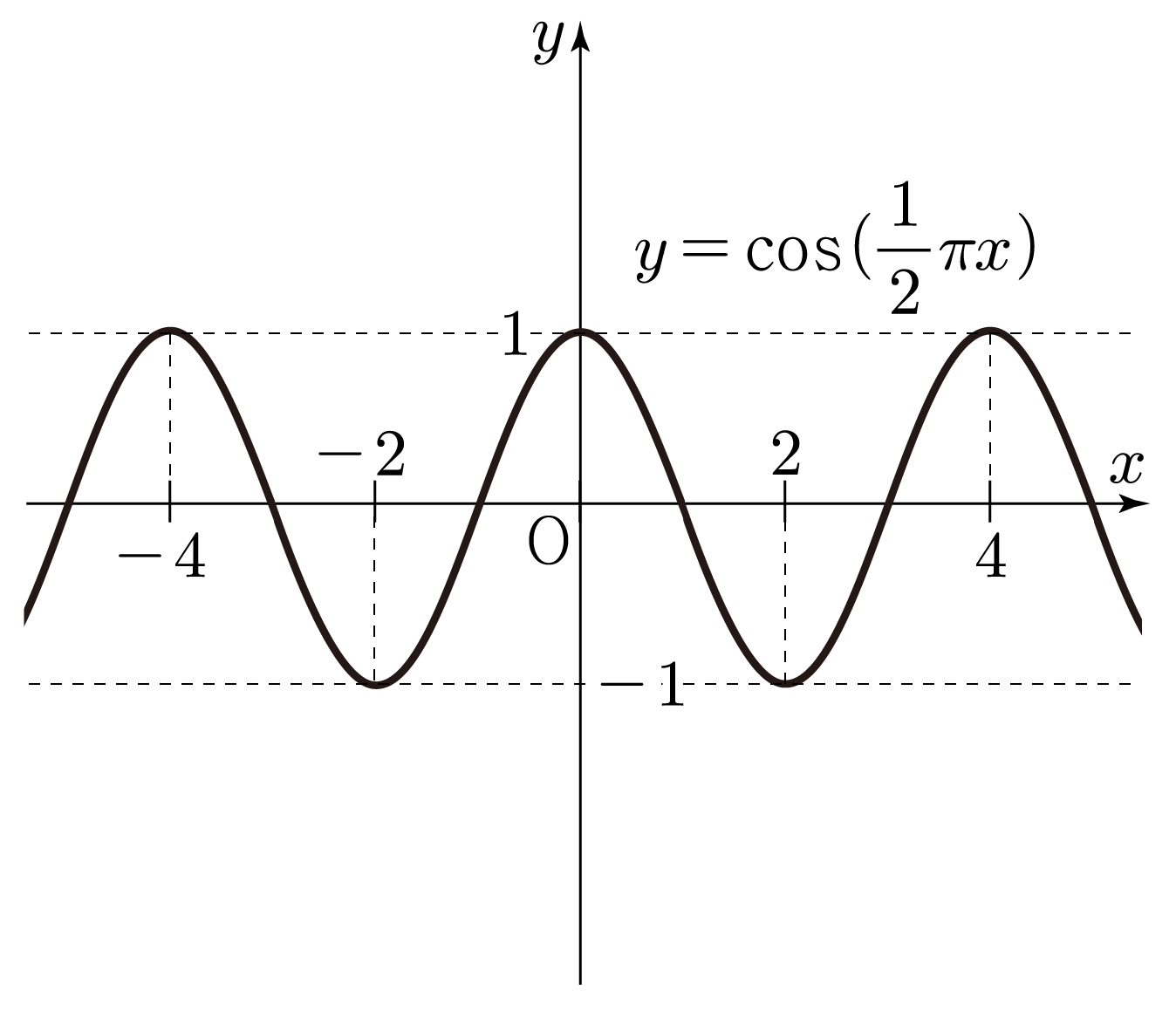
y=23cos(21π(x−2))의 그래프를 그려보자.
y=Acos(B(x−C))에서 A=23,B=21π,C=2이므로
- y는 최댓값 23과 최솟값 −23을 갖는다.
- 물결 모양이 21π2π=π4π=4를 주기로 반복된다.
- 아래의 y=23cos(21πx)의 그래프를 −x축 방향으로 2만큼 움직인 형태이다.
그러므로 y=23cos(21π(x+2))의 그래프를 그리면 아래와 같다.
따라서 y=23cos(21π(x−2))의 그래프를 그리면 아래와 같다.
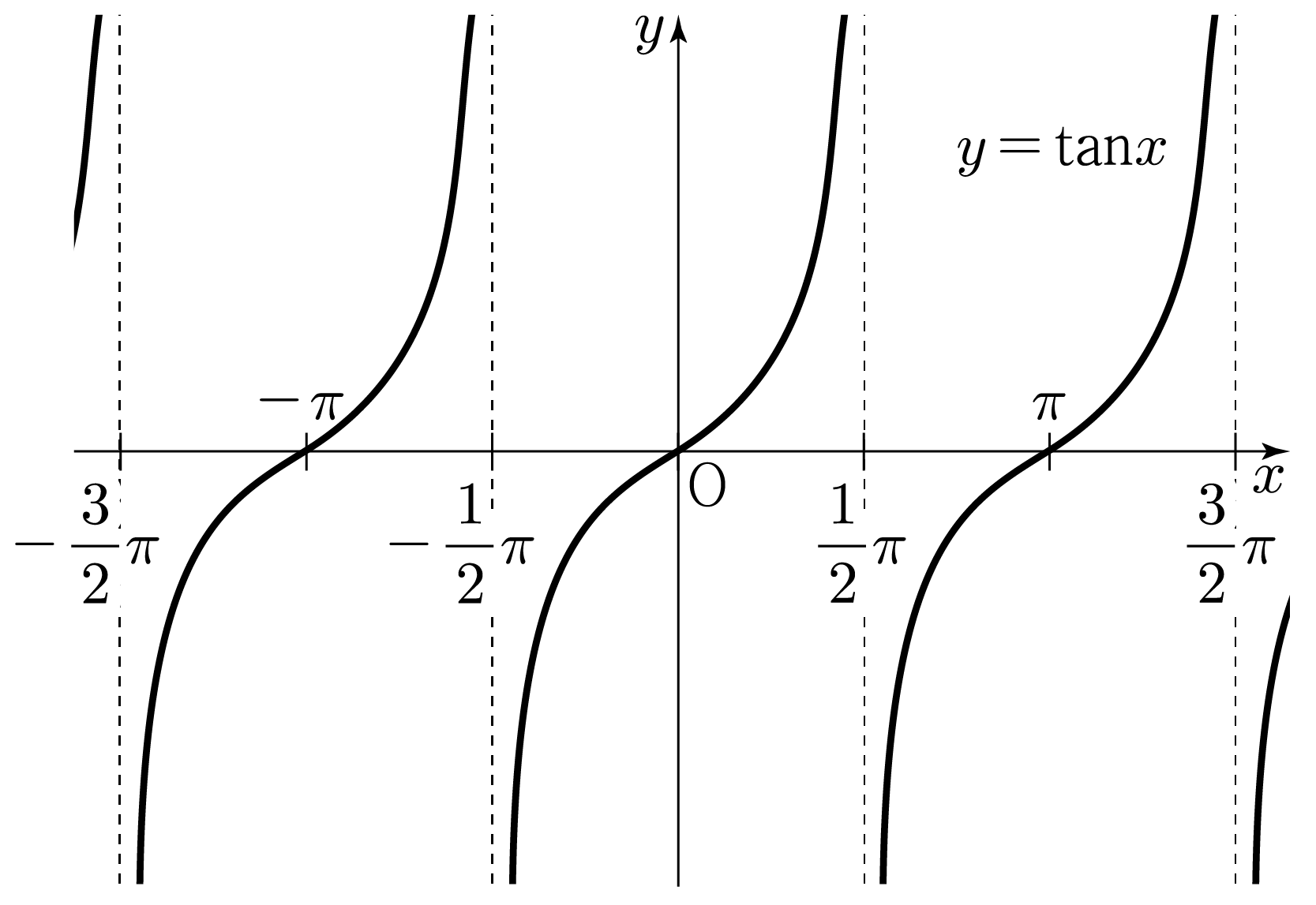
y=tanx의 그래프는 아래와 같다.
- y가 음의 무한대(−∞)나 양의 무한대(∞)로 가는 부분이 π를 주기로 반복된다.
- x=0일 때, y=0이다.
정답: $1$
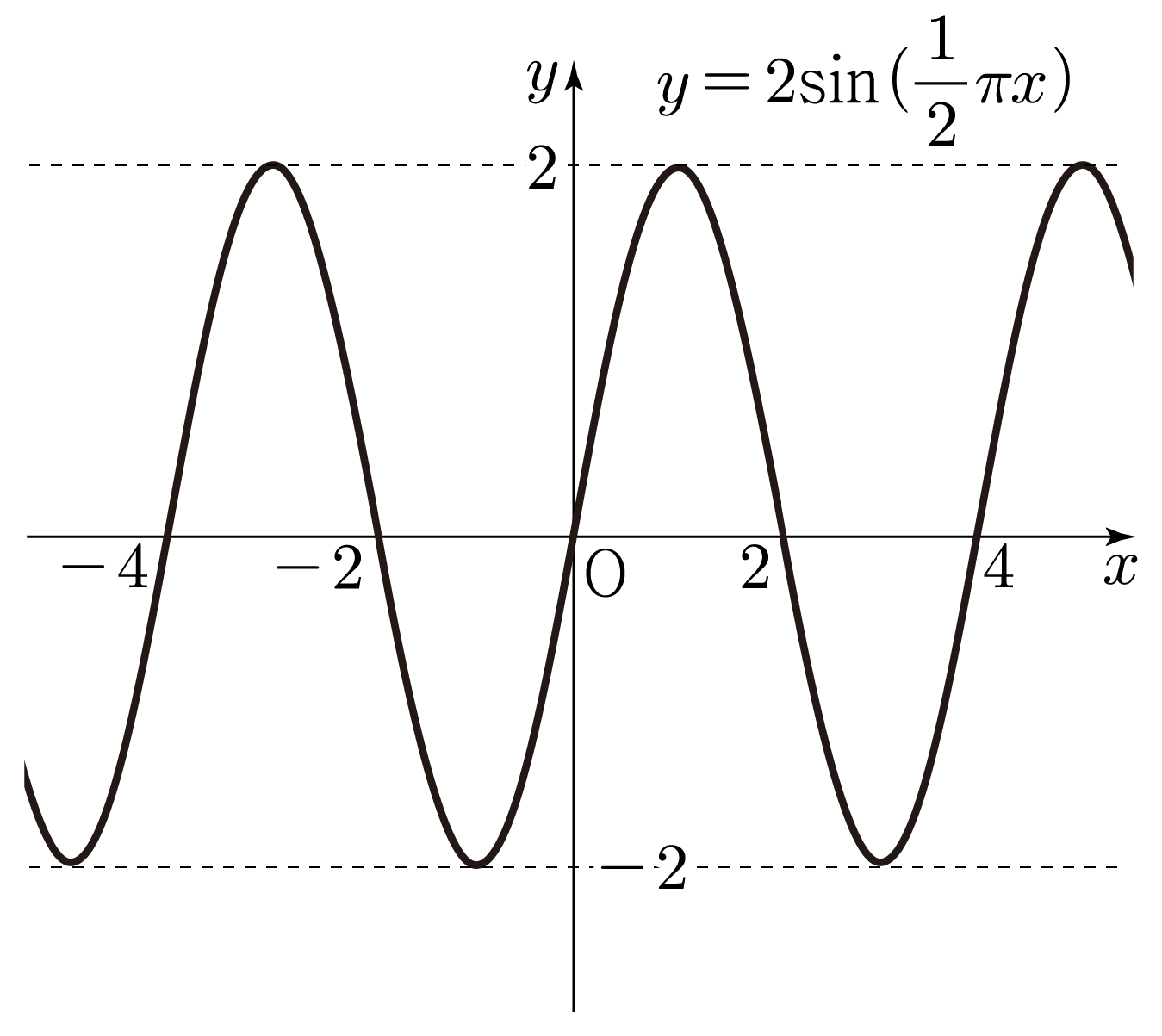
y=2sin(21πx)는 y=Asin(B(x−C))에서 A=2,B=21π,C=0이므로
- y는 최댓값 2와 최솟값 −2를 갖는다.
- 물결 모양이 21π2π=π4π=4를 주기로 반복된다.
그러므로 y=2sin(21πx)의 그래프를 그리면 아래와 같다.
따라서 정답은 1번이다.
정답: $3$
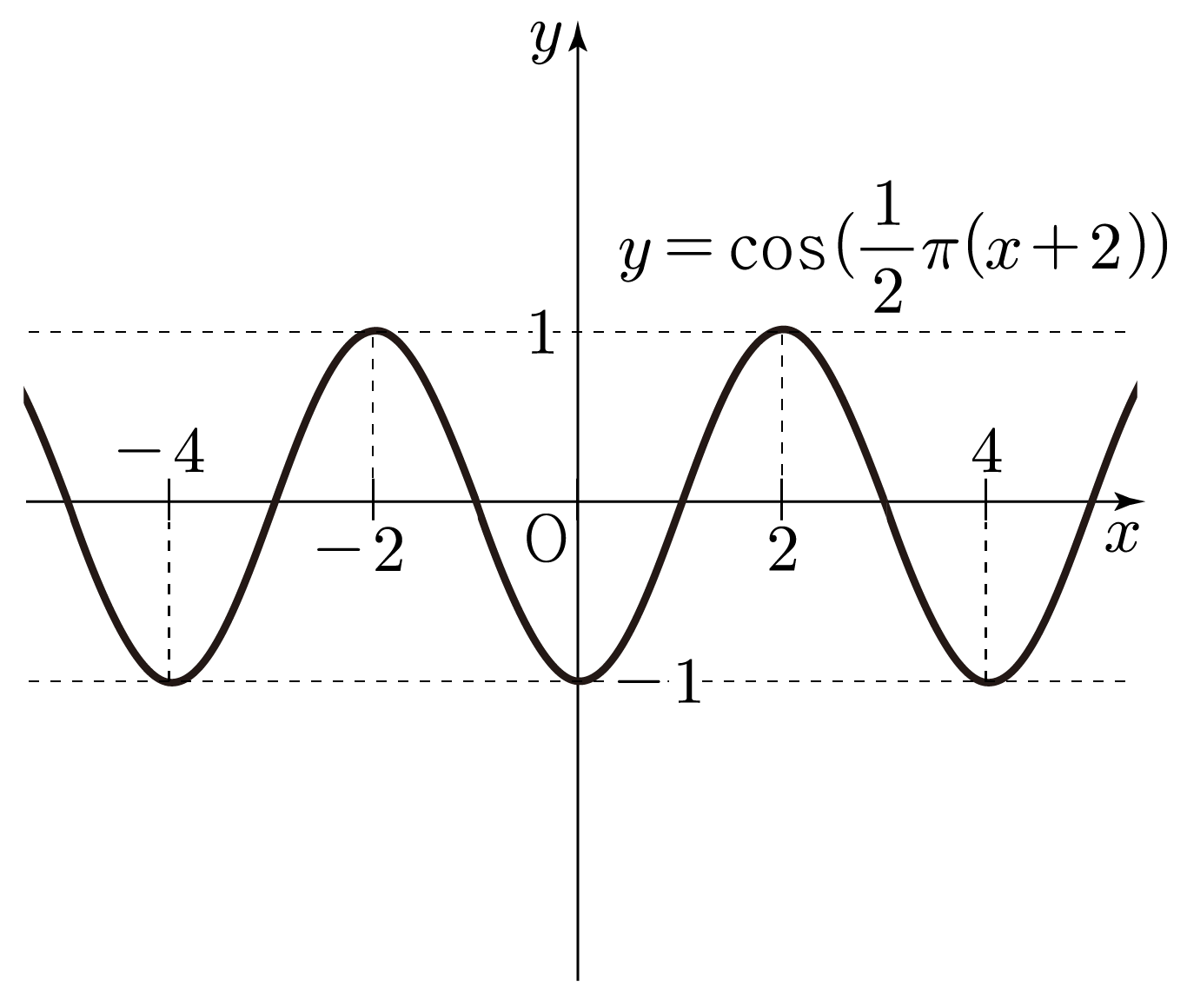
y=cos(21π(x+2))는 y=Acos(B(x−C))에서 A=1,B=21π,C=−2이므로
- y는 최댓값 1과 최솟값 −1을 갖는다.
- 물결 모양이 21π2π=π4π=4를 주기로 반복된다.
- 아래의 y=cos(21πx)의 그래프를 −x축 방향으로 2만큼 움직인 형태이다.
그러므로 y=cos(21π(x+2))의 그래프를 그리면 아래와 같다.
따라서 정답은 3번이다.
