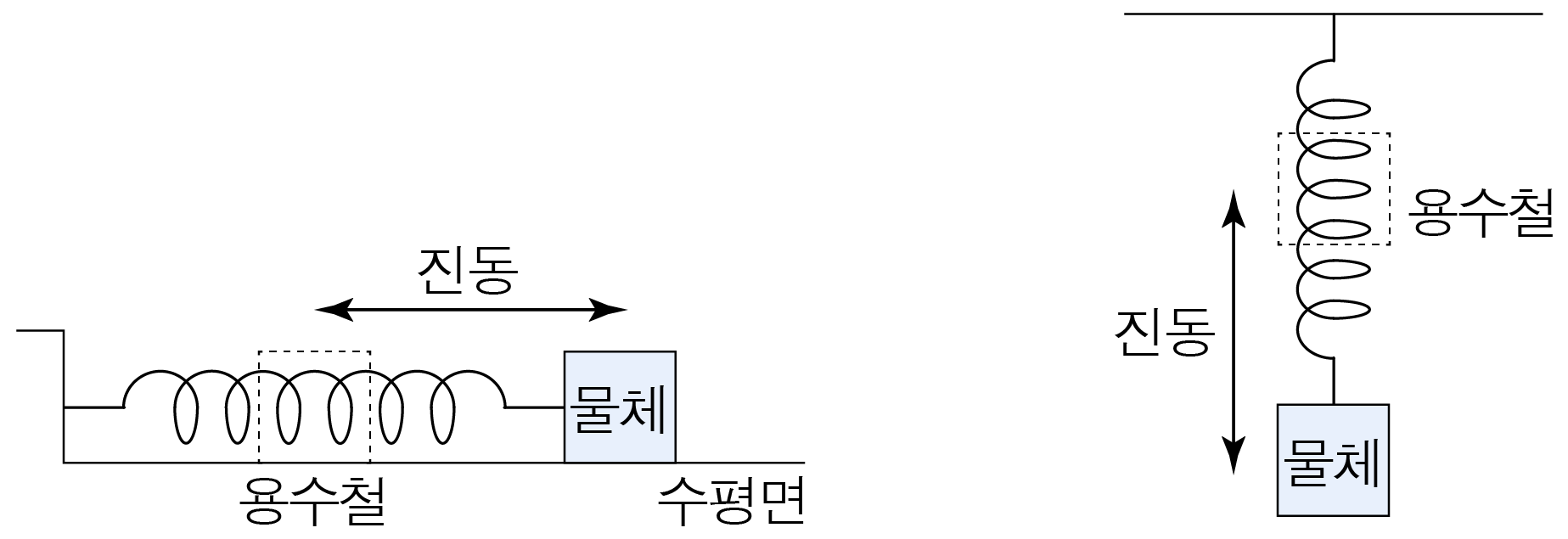
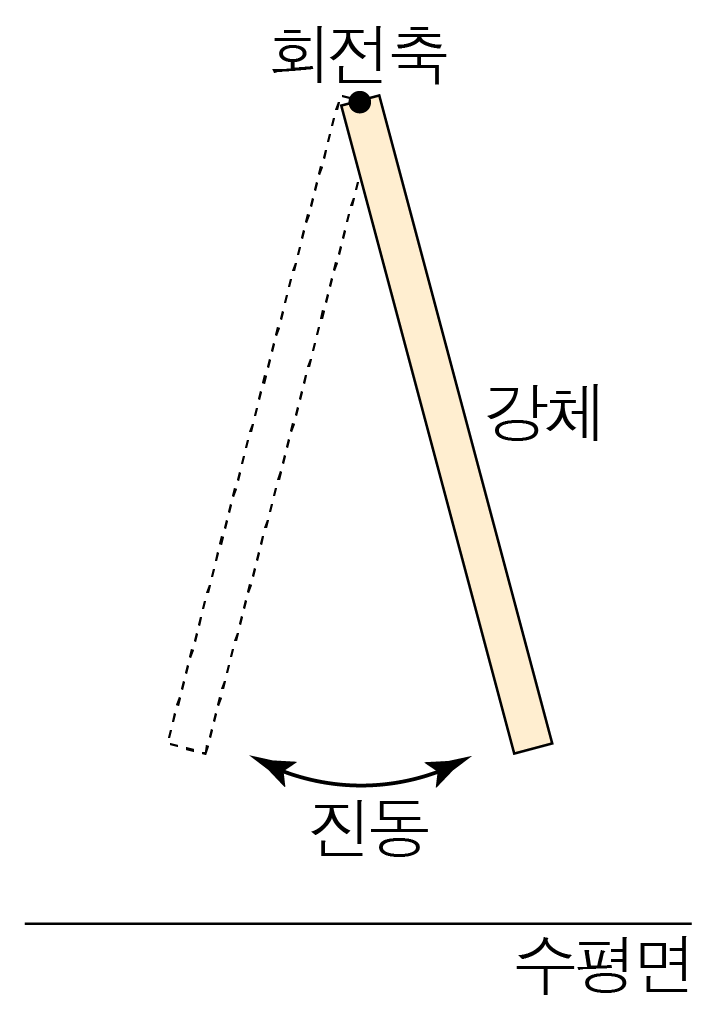
물체를 실, 용수철 또는 회전축 등에 매달아 흔들리도록 만든 장치이다.
진자에서 물체가 좌우 또는 위아래로 작은 각도 또는 변위를 이루며 규칙적으로 움직이는 진동을 단진동이라 한다.
진자의 주기는 물체가 한쪽 끝에서 반대쪽 끝까지 갔다가 다시 되돌아올 때까지 걸리는 시간이다.
물체에 한쪽 끝이 고정된 용수철을 달아 만든 진자이다.
물체의 질량을 m, 용수철 상수를 k라 할 때, 용수철 진자의 주기는 2πkm이고,
물체에 작용하는 알짜힘이 0인 지점(평형 지점)에서 물체의 운동 에너지는 최대가 된다.
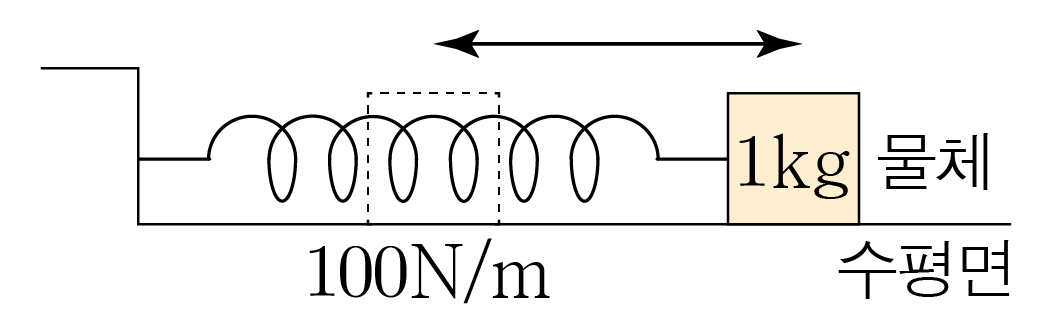
그림은 용수철 상수가 100N/m인 용수철에 질량이 1kg인 물체가 연결되어 주기가 T인 단진동을 하는 모습을 나타낸 것이다. T는? (단, 용수철의 질량과 물체의 크기는 무시한다.)
물체의 질량을 m, 용수철 상수를 k라 할 때, 용수철 진자의 주기는 2πkm이므로
T=2π100N/m1kg,
T=2π100(kg⋅m/s2)/m1kg,
T=2π100kg/s21kg,
T=2π102s−21,
T=2π×101s,
T=5πs이다.
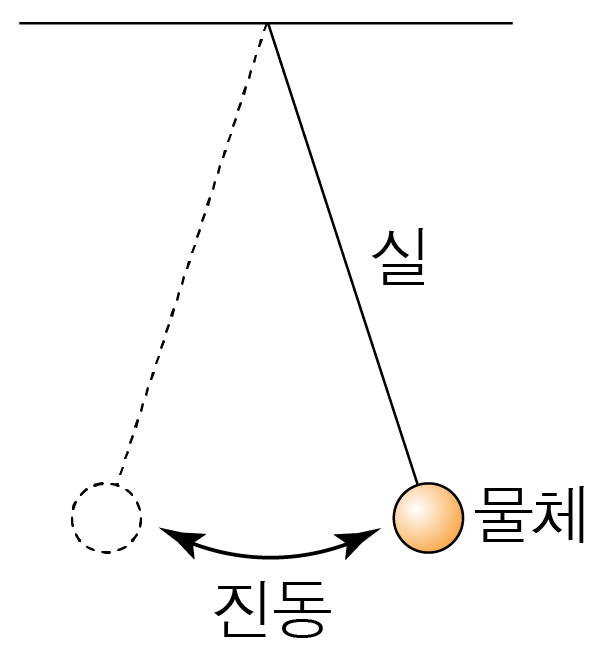
실에 물체를 매달고, 실과 물체 사이의 거리가 일정한 상태에서 진동하는 진자이다.
물체가 단진동하는 경우, 실의 길이를 L, 중력 가속도를 g라 할 때, 단진자의 주기는 2πgL이다.
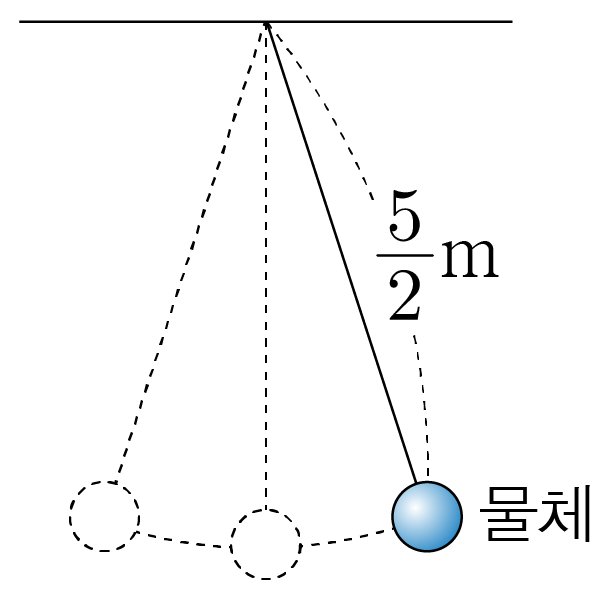
그림은 길이가 25m인 실에 물체가 연결되어 주기가 T인 단진동을 하는 모습을 나타낸 것이다. T는? (단, 중력 가속도는 10m/s2이고, 물체의 크기와 실의 질량은 무시한다.)
실의 길이를 L, 중력 가속도를 g라 할 때, 단진자의 주기는 2πgL이므로
T=2π10m/s225m,
T=2π10s−225,
T=2π20s−25,
T=2π4s−21,
T=2π×21s,
T=πs이다.
강체가 회전축을 중심으로 진동하는 진자이다.
물체가 단진동하는 경우, 강체의 질량, 관성 모멘트, 회전축으로부터 질량 중심까지의 거리를 각각 m, I, d라 하고, 중력 가속도를 g라 할 때, 물리 진자의 주기는 2πmgdI이다.
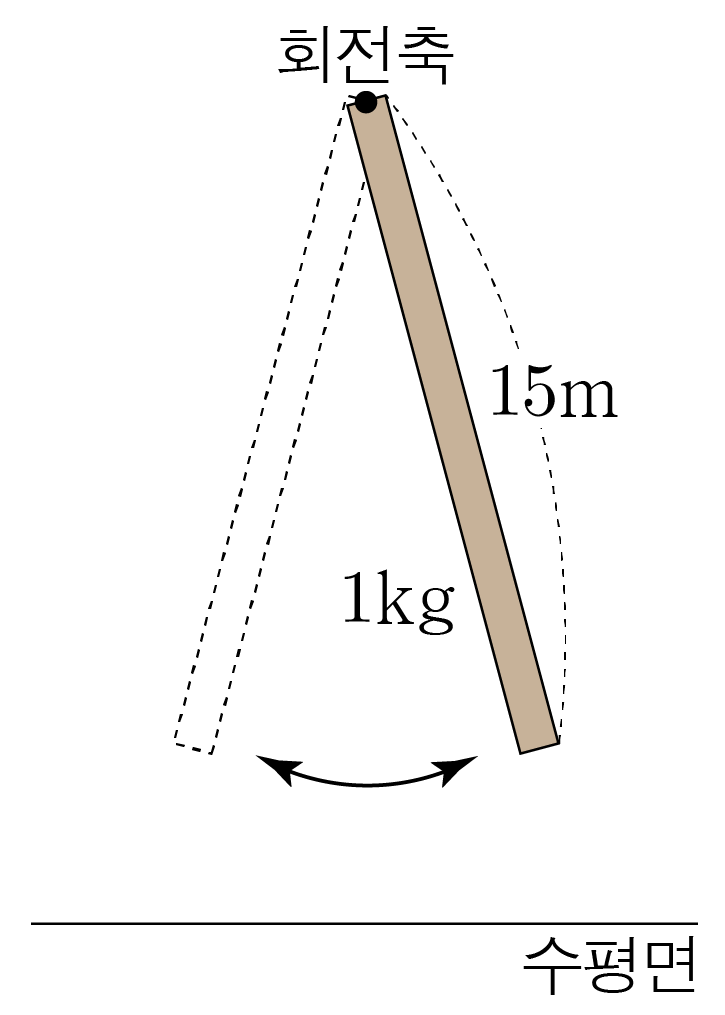
그림은 질량과 길이가 각각 1kg, 15m인 균일한 막대가 고정된 회전축에 대해 주기 T로 단진동하는 물리 진자를 나타낸 것이다. 회전축에 대한 막대의 관성 모멘트가 75kg⋅m2일 때, T는? (단, 중력 가속도는 10m/s2이고, 막대의 굵기는 무시한다.)
강체의 질량, 관성 모멘트, 회전축으로부터 질량 중심까지의 거리를 각각 m, I, d라 하고, 중력 가속도를 g라 할 때, 물리 진자의 주기는 2πmgdI이다.
m=1kg, d=215m, I=75kg⋅m2이므로
T=2π1kg×10m/s2×215m75kg⋅m2,
T=2π10kg⋅m/s2×215m75kg⋅m2,
T=2π75kg⋅m2/s275kg⋅m2,
T=2π75s−275,
T=2πs−21,
T=2π×s−11,
T=2πs이다.
정답: $3$
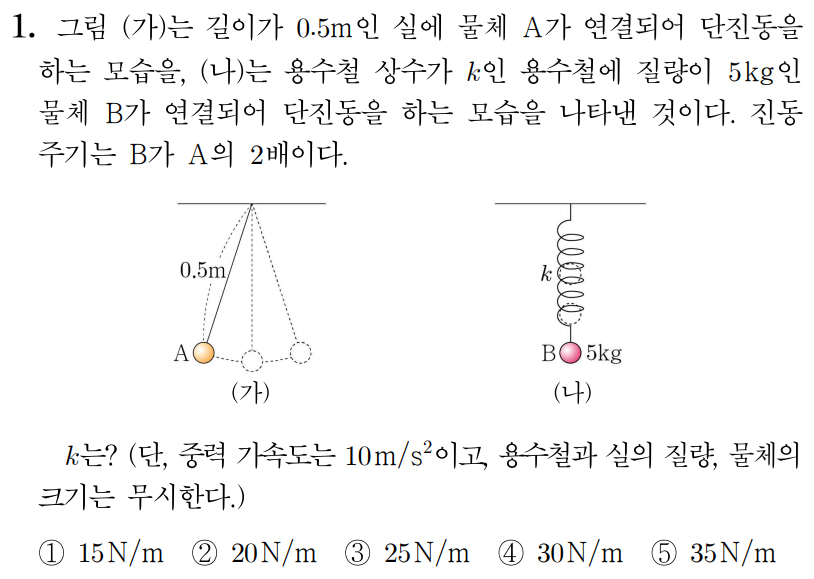
A, B의 주기를 각각 TA, TB라 하자.
실의 길이를 L, 중력 가속도를 g라 할 때, 단진자의 주기는 2πgL이므로
TA=2π10m/s20.5m,
TA=2π10s−20.5,
TA=2π10×2s−20.5×2,
TA=2π20s−21이다.
물체의 질량을 m, 용수철 상수를 k라 할 때, 용수철 진자의 주기는 2πkm이므로
TB=2πk5kg이다.
진동 주기는 B가 A의 2배이므로
2πk5kg=2×2π20s−21,
k5kg=220s−21,
k5kg=20s−222,
k5kg=20s−24,
k5kg=5s−21,
k5kg=5s−21,
5kg×5s−2=k,
k=25kg/s2,
k=25(kg⋅m/s2)/m,
k=25N/m이다.
따라서 정답은 3번이다.

정답: $2$
강체(막대와 물체로 이루어진 계)의 질량, 관성 모멘트, 회전축으로부터 질량 중심까지의 거리를 각각 m, I, d라 하고, 중력 가속도를 g라 할 때, 물리 진자의 주기는 2πmgdI이다.
1. m 구하기:
m=6kg+3kg=9kg이다.
2. d 구하기:
막대와 물체를 각각 1, 2번째 물체라 하면 m1=6kg, m2=3kg이고,
i=1∑2mi=m1+m2=6kg+3kg=9kg이다.
회전축을 기준점이라고 하면 r1=21m, r2=1m이므로
i=1∑2miri=m1r1+m2r2,
i=1∑2miri=(6kg×21m)+(3kg×1m),
i=1∑2miri=3kg⋅m+3kg⋅m,
i=1∑2miri=6kg⋅m이다.
i=1∑2mii=1∑2miri=9kg6kg⋅m=32m이므로 d=32m이다.
3. I 구하기:
회전축에 대한 막대의 관성 모멘트는 2kg⋅m2이므로 막대와 물체로 이루어진 계의 관성 모멘트는 2kg⋅m2에 물체의 관성 모멘트를 추가한 값이다.
그러므로 I=2kg⋅m2+m2r22,
I=2kg⋅m2+3kg×(1m)2,
I=2kg⋅m2+3kg⋅m2,
I=5kg⋅m2이다.
T=2πmgdI이므로
T=2π9kg×10m/s2×32m5kg⋅m2,
T=2π90kg⋅m/s2×32m5kg⋅m2,
T=2π60kg⋅m2/s25kg⋅m2,
T=2π60s−25,
T=2π12s−21,
T=π12s−24,
T=π3s−21,
T=3s−1π,
T=3πs이다.
따라서 정답은 2번이다.