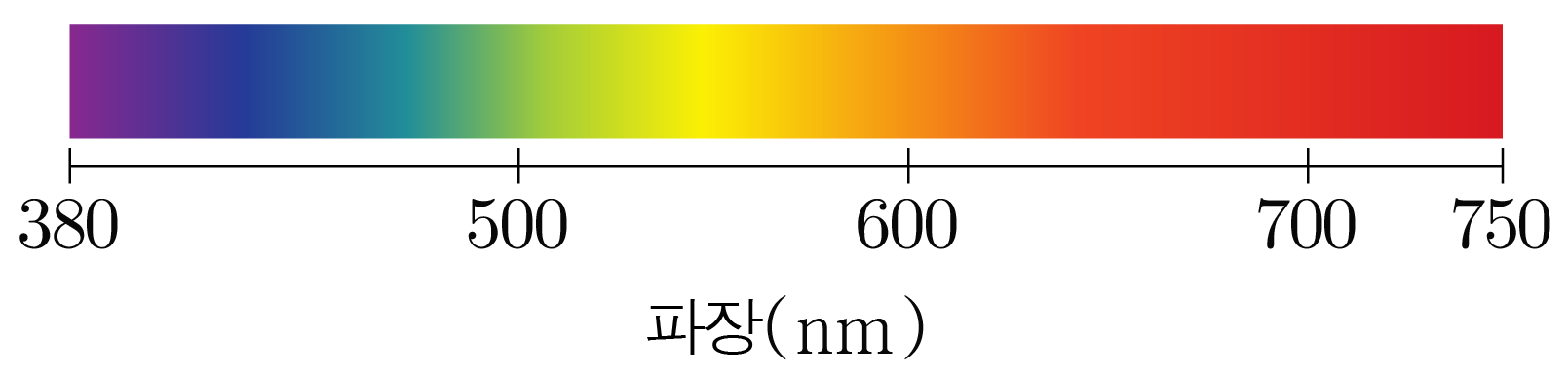
인간의 눈으로 볼 수 있는 빛이다.380 ∼ 750 n m 3 8 0 ∼ 7 5 0 n m < < < < < < < < < <
모든 파장의 빛을 흡수하는 동시에 흡수한 에너지를 모두 복사 에너지로 방출하는 물체이다.
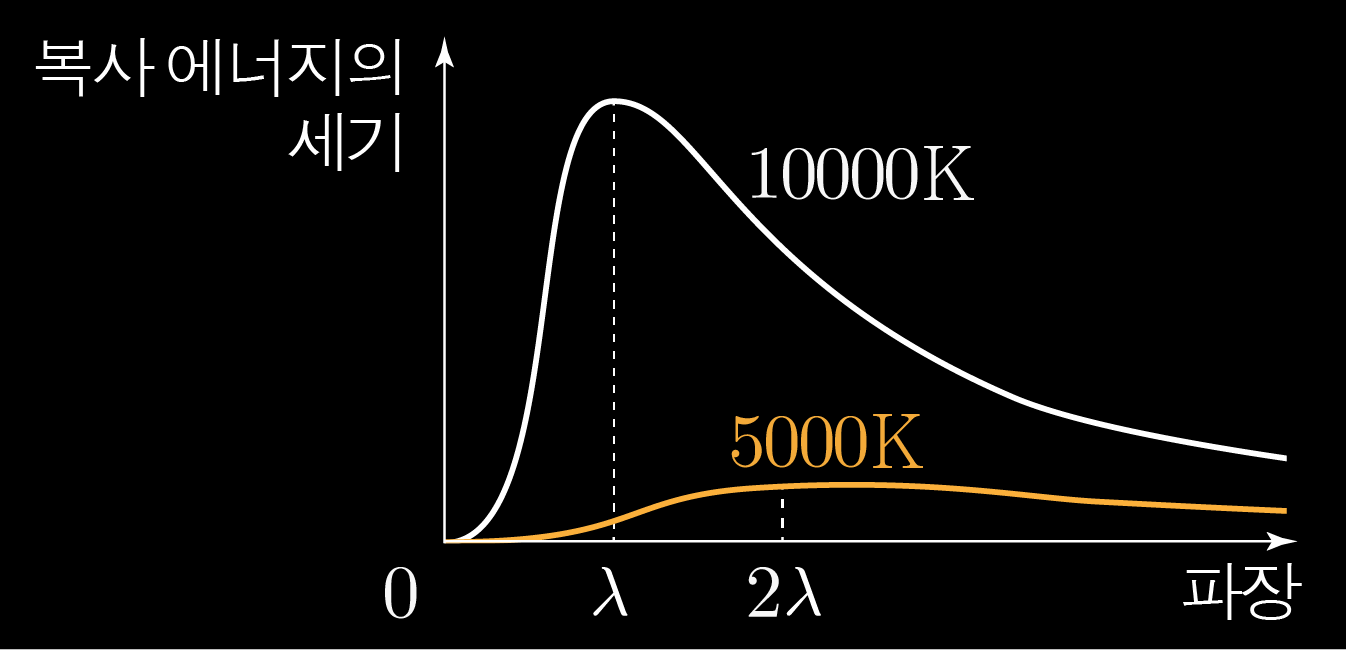
방출하는 복사 에너지의 세기는 빛의 파장에 따라 달라진다.
흑체가 가장 강하게 복사 에너지(최대 복사 에너지)를 방출하는 파장을 λ max λ m a x a a T T λ max = a T λ m a x = T a ( a = 2.898 × 1 0 − 3 m ⋅ K ) ( a = 2 . 8 9 8 × 1 0 − 3 m ⋅ K )
흑체가 단위 시간당 단위 면적에서 방출하는 복사 에너지의 세기를 파장에 따라 나타낸 것이다.
빈의 변위 법칙 λ max = a T λ m a x = T a λ max λ m a x T T
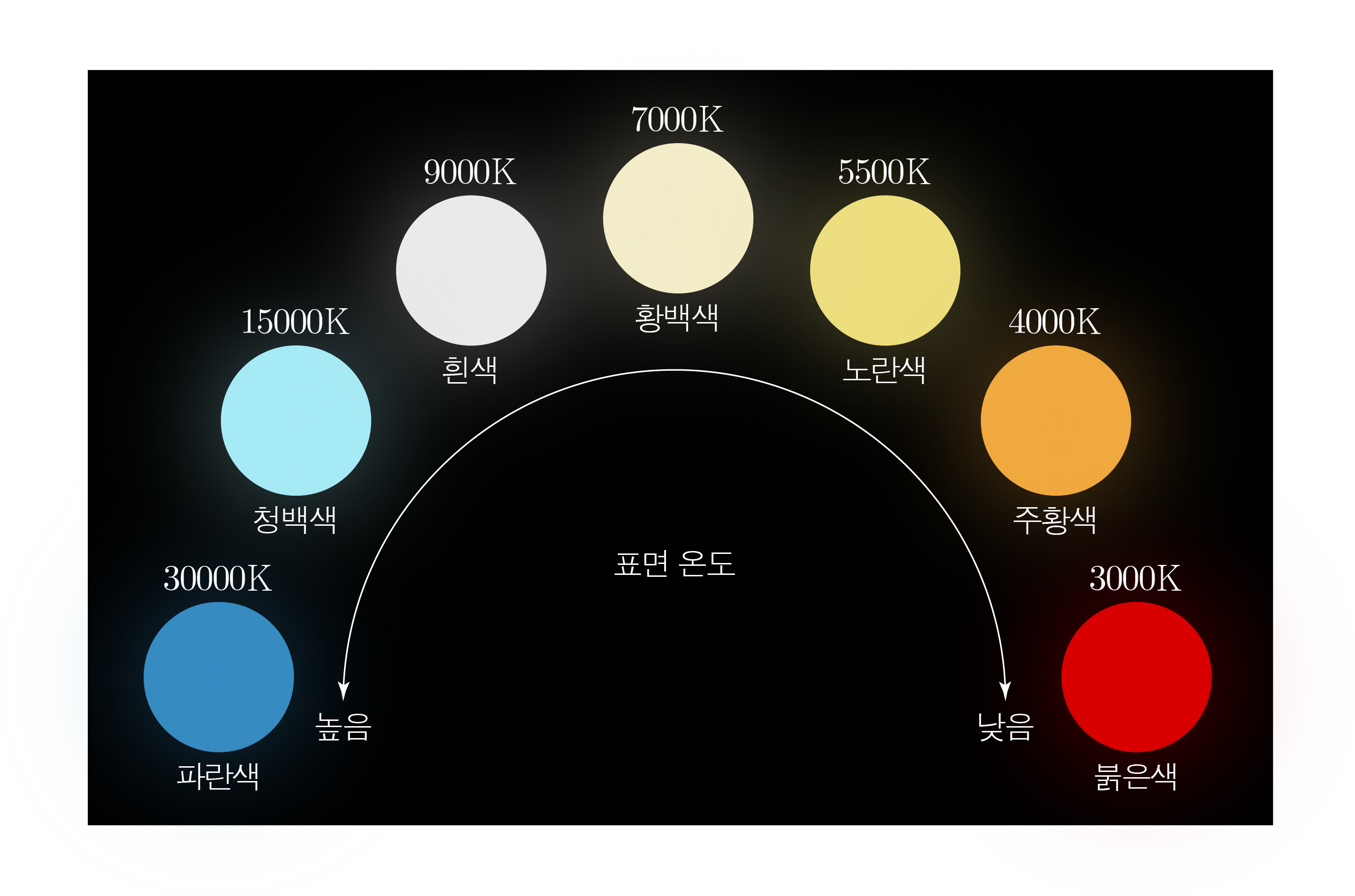
별은 흑체와 비슷하게 복사하므로 별의 표면 온도가 높을수록 최대 복사 에너지를 방출하는 파장이 짧아진다.
따라서 별은 표면 온도가 높을수록 파장이 짧은 파란색을 띠고, 표면 온도가 낮을수록 파장이 긴 붉은색을 띤다.
그림은 표면 온도가 15000 K 1 5 0 0 0 K λ max λ m a x n m n m 3 × 1 0 − 3 m ⋅ K 3 × 1 0 − 3 m ⋅ K
빈의 변위 상수를 a a T T λ max = a T λ m a x = T a λ max = 3 × 1 0 − 3 m ⋅ K 15000 K , λ m a x = 1 5 0 0 0 K 3 × 1 0 − 3 m ⋅ K , λ max = 3 × 1 0 − 3 m 15000 , λ m a x = 1 5 0 0 0 3 × 1 0 − 3 m , λ max = 1 × 1 0 − 3 m 5000 , λ m a x = 5 0 0 0 1 × 1 0 − 3 m , λ max = 1 × 1 0 − 3 × 1 0 − 3 m 5000 × 1 0 − 3 , λ m a x = 5 0 0 0 × 1 0 − 3 1 × 1 0 − 3 × 1 0 − 3 m , λ max = 1 × 1 0 − 6 m 5 , λ m a x = 5 1 × 1 0 − 6 m , λ max = 1 5 × 1 0 − 6 m , λ m a x = 5 1 × 1 0 − 6 m , λ max = 1 5 × 1 0 3 × 1 0 − 9 m , λ m a x = 5 1 × 1 0 3 × 1 0 − 9 m , λ max = 200 × 1 0 − 9 m , λ m a x = 2 0 0 × 1 0 − 9 m , λ max = 200 n m λ m a x = 2 0 0 n m
1번 문항 정답 및 해설 보기
정답: $5$
빈의 변위 법칙 λ max = a T λ m a x = T a λ max λ m a x T T λ max λ m a x A < B < C A < B < C C < B < A C < B < A T C < T B < T A T C < T B < T A
따라서 정답은 5 5
2번 문항 정답 및 해설 보기
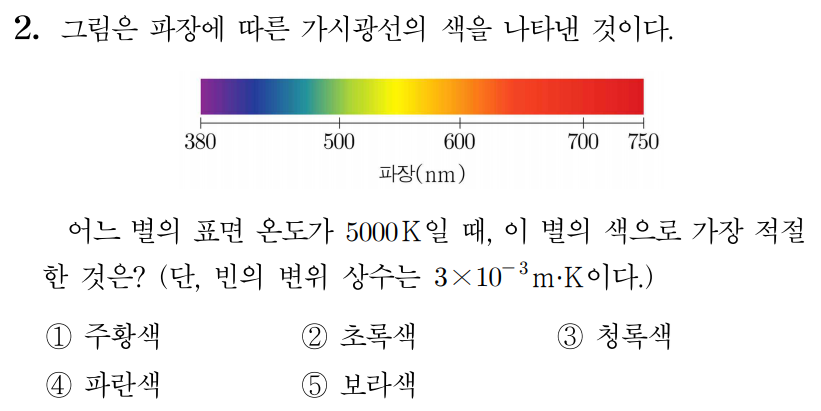
정답: $1$
빈의 변위 상수를 a a T T λ max = a T λ m a x = T a λ max = 3 × 1 0 − 3 m ⋅ K 5000 K , λ m a x = 5 0 0 0 K 3 × 1 0 − 3 m ⋅ K , λ max = 3 × 1 0 − 3 m 5000 , λ m a x = 5 0 0 0 3 × 1 0 − 3 m , λ max = 3 × 1 0 − 3 × 1 0 − 3 m 5000 × 1 0 − 3 , λ m a x = 5 0 0 0 × 1 0 − 3 3 × 1 0 − 3 × 1 0 − 3 m , λ max = 3 × 1 0 − 6 m 5 , λ m a x = 5 3 × 1 0 − 6 m , λ max = 3 × 1 0 − 6 × 2 m 5 × 2 , λ m a x = 5 × 2 3 × 1 0 − 6 × 2 m , λ max = 6 × 1 0 − 6 m 10 , λ m a x = 1 0 6 × 1 0 − 6 m , λ max = 0.6 × 1 0 − 6 m , λ m a x = 0 . 6 × 1 0 − 6 m , λ max = 0.6 × 1 0 3 × 1 0 − 9 m , λ m a x = 0 . 6 × 1 0 3 × 1 0 − 9 m , λ max = 600 × 1 0 − 9 m , λ m a x = 6 0 0 × 1 0 − 9 m , λ max = 600 n m λ m a x = 6 0 0 n m 600 n m 6 0 0 n m
따라서 정답은 1 1