2π를 파동의 파장 λ로 나눈 (λ2π) 물리량이다.
기본 단위는 rad/m=m−1이고, 기호로는 k로 나타낸다.
2π에 파동의 진동수 f를 곱한 (2πf) 물리량이다.
기본 단위는 rad/s=s−1이고, 기호로는 ω로 나타낸다.
단위 길이당 질량이다. 질량이 m, 길이가 L인 물체의 선밀도는 Lm이다.
기본 단위는 kg/m이고, 기호로는 μ로 나타낸다.
어느 줄의 질량이 1kg이고, 길이가 100m일 때, 선밀도 μ를 구해보자.
질량이 m, 길이가 L인 물체의 선밀도는 Lm이므로 μ=100m1kg=0.01kg/m이다.
파동의 파장과 진동수를 각각 λ, f라 할 때, 파동의 속력 v=λf이다.
줄에 걸린 장력을 T, 선밀도를 μ라 할 때, 줄에서 횡파의 속력 v=μT이다.
파동이 위치와 시간에 따라 어떻게 변하는지를 함수로 나타낸 것이다.
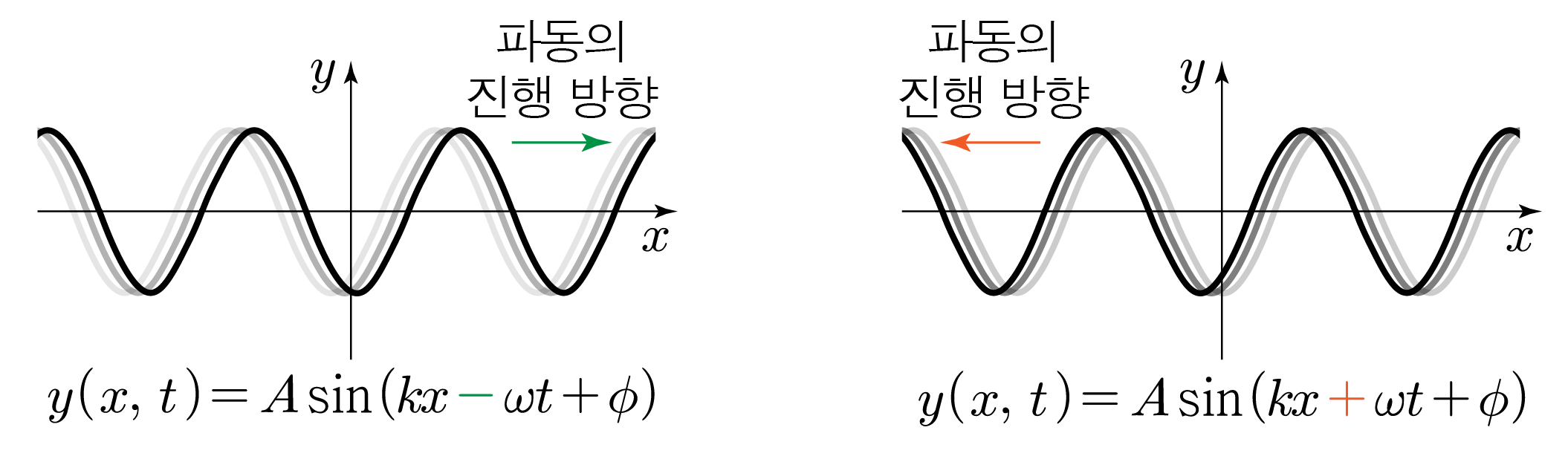
x 축과 나란한 방향으로 진행하고, 파수가 k, 각진동수가 ω인 파동의 변위 y를 위치 x와 시간 t에 따라 나타낸 파동 함수는 아래와 같다.
- +x 방향으로 진행하는 경우: y(x,t)=Asin(kx−ωt+ϕ)
- −x 방향으로 진행하는 경우: y(x,t)=Asin(kx+ωt+ϕ)
y(x,t)는 위치 x, 시간 t일 때의 변위를 의미하며,
A는 진폭, ϕ는 파동이 어느 위치에서 시작하는지를 나타내는 초기 위상에 해당한다.
다음은 파동의 변위 y를 위치 x와 시간 t에 따라 나타낸 것이다.
y(x,t)=3sin(π(x−4t))
이 파동의 진행 방향, 진폭 A, 파장 λ, 진동수 f, 주기 T, 속력 v를 구해보자. (단, x, y 축의 단위는 m이다.)
y(x,t)=3sin(π(x−4t))=3sin(πx−4πt)이므로
파동은 +x 방향으로 진행하고, A=3m, 파수 k=πm−1, 각진동수 ω=4πs−1이다.
-
파장 구하기:
k=λ2π이므로
πm−1=λ2π,
1m−1=λ2,
λm−1=2,
λ=2m이다.
-
진동수 구하기:
ω=2πf이므로
4πs−1=2πf,
f=2s−1=2Hz이다.
-
주기 구하기:
f=T1이므로
2s−1=T1,
2Ts−1=1,
Ts−1=21,
T=21s이다.
-
속력 구하기:
v=λf이므로
v=2m×2s−1,
v=4m/s이다.
정답: $2$
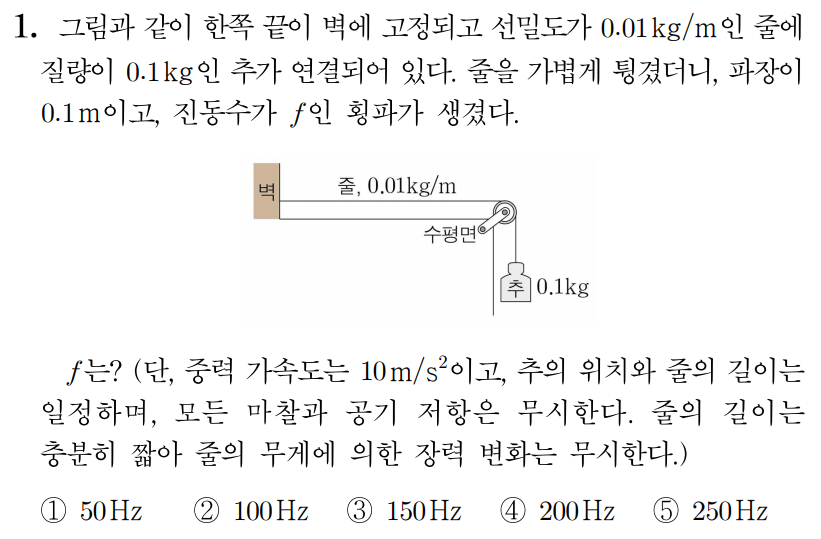
파동의 파장과 진동수를 각각 λ, f라 할 때, 파동의 속력 v=λf이고,
줄에 걸린 장력을 T, 선밀도를 μ라 할 때, 줄에서 횡파의 속력 v=μT이므로
v=λf=μT이다.
T=0.1kg×10m/s2=1kg⋅m/s2이므로
λf=μT에서
0.1m×f=0.01kg/m1kg⋅m/s2,
0.1m×f=0.01m−11m/s2,
0.1m×f=0.011m2/s2,
0.1m×f=0.01×1001×100m2/s2,
0.1m×f=100m2/s2,
0.1m×f=10m/s,
0.1×f=10s−1,
f=100s−1=100Hz이다.
따라서 정답은 2번이다.

정답: $5$
ㄱ. y(x,t)=3sin(4πx+πt+π)에서 πt는 양(+)의 부호를 가지므로 파동의 진행 방향은 −x 방향이다. (O)
ㄴ. y(x,t)=3sin(4πx+πt+π)에서 파동의 진폭 A=3m, 파수 k=4πm−1, 각진동수 ω=πs−1이다.
-
진동수 구하기:
파동의 진동수를 f라 할 때, ω=2πf이므로
πs−1=2πf,
1s−1=2f,
f=21s−1=21Hz이다.
-
주기 구하기:
파동의 주기를 T라 할 때, f=T1이므로
21s−1=T1,
21Ts−1=1,
Ts−1=2,
T=2s이다. (O)
ㄷ. 파동의 파장을 λ라 할 때, k=λ2π이므로
4πm−1=λ2π,
2m−1=λ1,
2λm−1=1,
2λ=1m,
λ=21m이다.
- 속력 구하기:
v=λf이므로
v=21m×21s−1,
v=41m/s이다. (O)
따라서 정답은 5번이다.