액체, 기체와 같이 흐를 수 있는 물질이다.
단위 부피당 질량이다. 질량이 m m V V m V V m k g / m 3 k g / m 3 ρ ρ
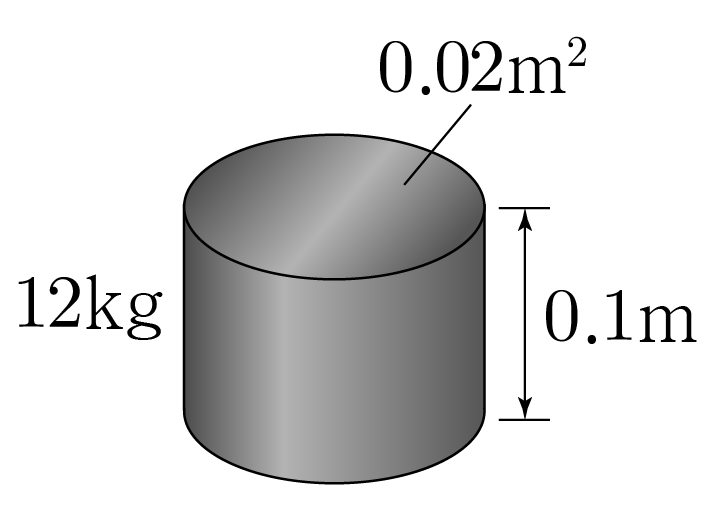
그림은 단면적이 0.02 m 2 0 . 0 2 m 2 0.1 m 0 . 1 m 12 k g 1 2 k g
물체의 질량은 12 k g 1 2 k g 0.02 m 2 × 0.1 m = 0.002 m 3 0 . 0 2 m 2 × 0 . 1 m = 0 . 0 0 2 m 3 12 k g 0.002 m 3 = 6 k g 0.001 m 3 = 6000 k g / m 3 0 . 0 0 2 m 3 1 2 k g = 0 . 0 0 1 m 3 6 k g = 6 0 0 0 k g / m 3
단위 면적에 수직으로 작용하는 힘의 크기이다.N / m 2 = P a N / m 2 = P a P a P a P P
크기가 F F S S P P P = F S P = S F
기체 입자와 같이 압력을 가해줄 물질이 존재하지 않는 진공에서 압력은 0 0
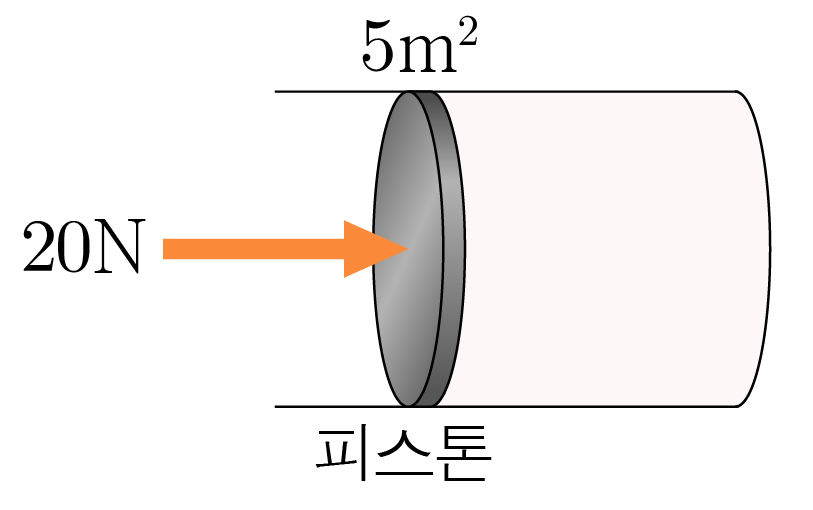
그림은 단면적이 5 m 2 5 m 2 20 N 2 0 N
크기가 F F S S P P P = F S P = S F P = 20 N 5 m 2 = 4 N / m 2 = 4 P a P = 5 m 2 2 0 N = 4 N / m 2 = 4 P a
유체의 밀도를 ρ ρ g g h h ρ g h ρ g h
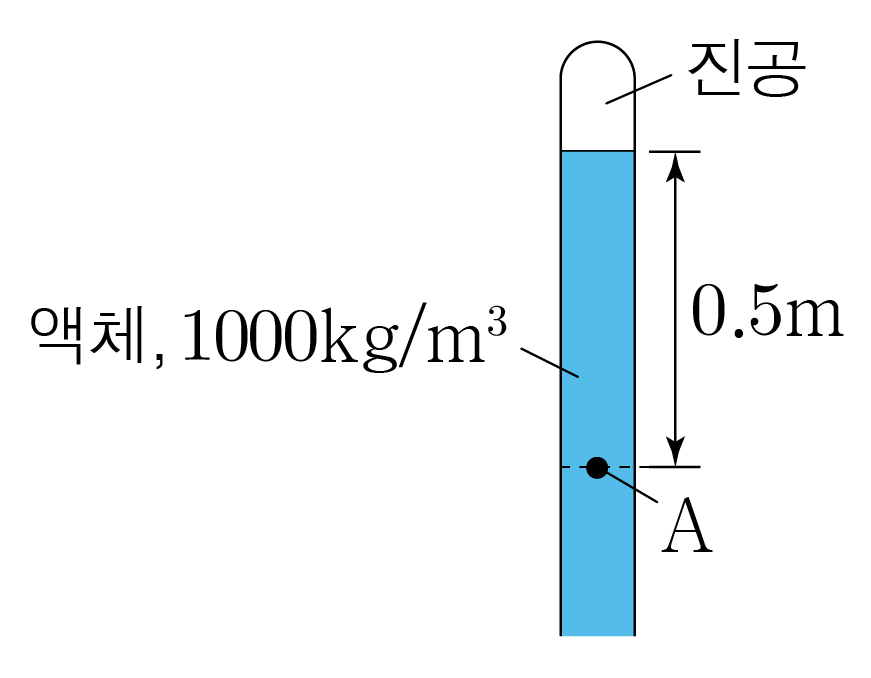
그림과 같이 유리관 안에 밀도가 1000 k g / m 3 1 0 0 0 k g / m 3 A A 0.5 m 0 . 5 m A A 10 m / s 2 1 0 m / s 2
진공에서는 물질이 존재하지 않으므로 압력은 0 0
유체의 밀도는 1000 k g / m 3 1 0 0 0 k g / m 3 10 m / s 2 1 0 m / s 2 A A 0.5 m 0 . 5 m A A P P P = 1000 k g / m 3 × 10 m / s 2 × 0.5 m , P = 1 0 0 0 k g / m 3 × 1 0 m / s 2 × 0 . 5 m , P = 1000 k g / m 3 × 10 N / k g × 0.5 m , P = 1 0 0 0 k g / m 3 × 1 0 N / k g × 0 . 5 m , P = 10000 N / m 3 × 0.5 m , P = 1 0 0 0 0 N / m 3 × 0 . 5 m , P = 5000 N / m 2 P = 5 0 0 0 N / m 2
따라서 A A 0 0 + 5000 N / m 2 = 5000 N / m 2 + 5 0 0 0 N / m 2 = 5 0 0 0 N / m 2
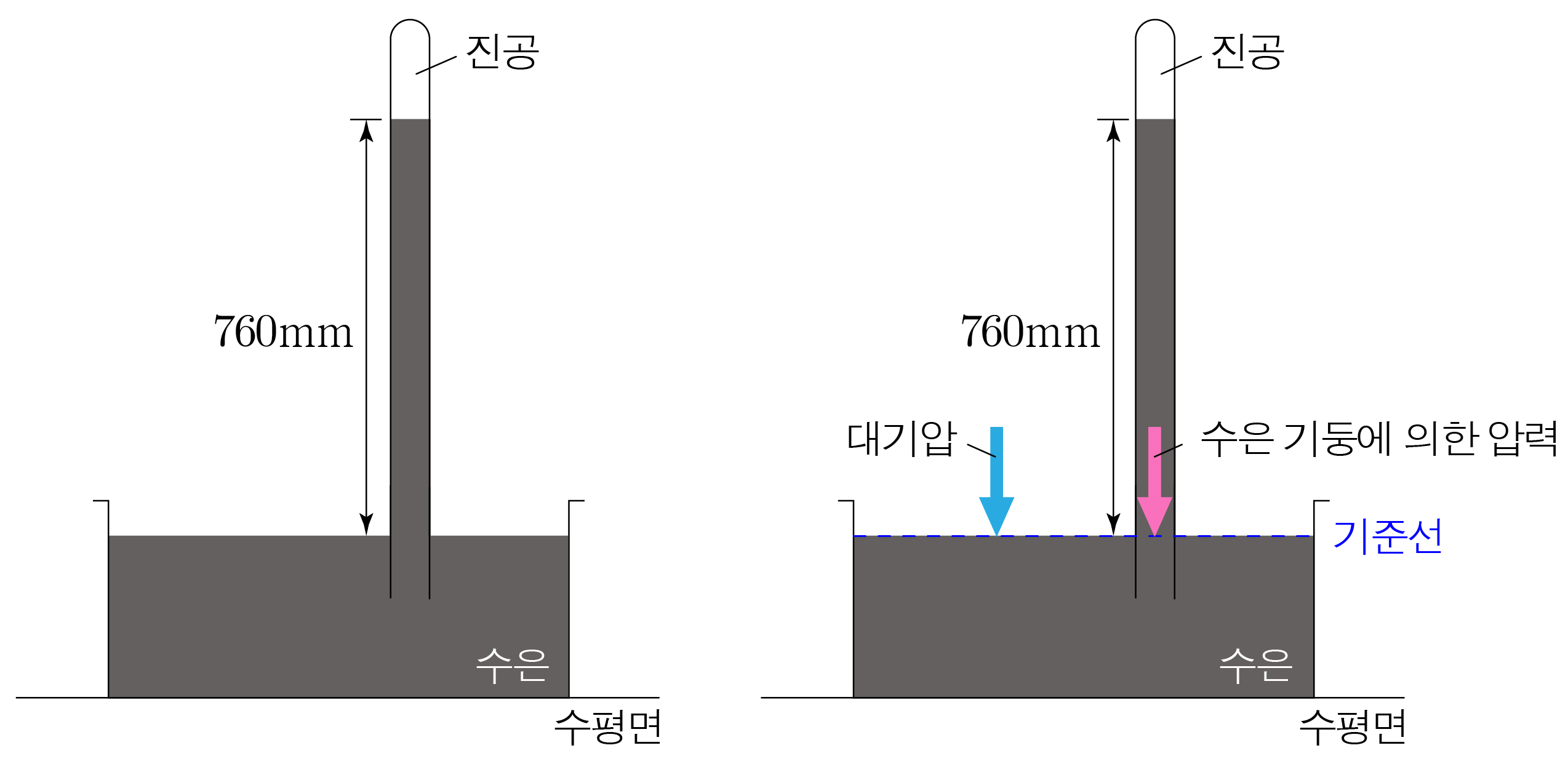
지구의 대기가 가하는 압력이다.1 1 a t m a t m 1 1 = 1 a t m = 1 a t m H g H g 760 m m 7 6 0 m m 1 1 = 1 a t m = 760 m m H g = 101300 N / m 2 = 1013 h P a = 1 a t m = 7 6 0 m m H g = 1 0 1 3 0 0 N / m 2 = 1 0 1 3 h P a
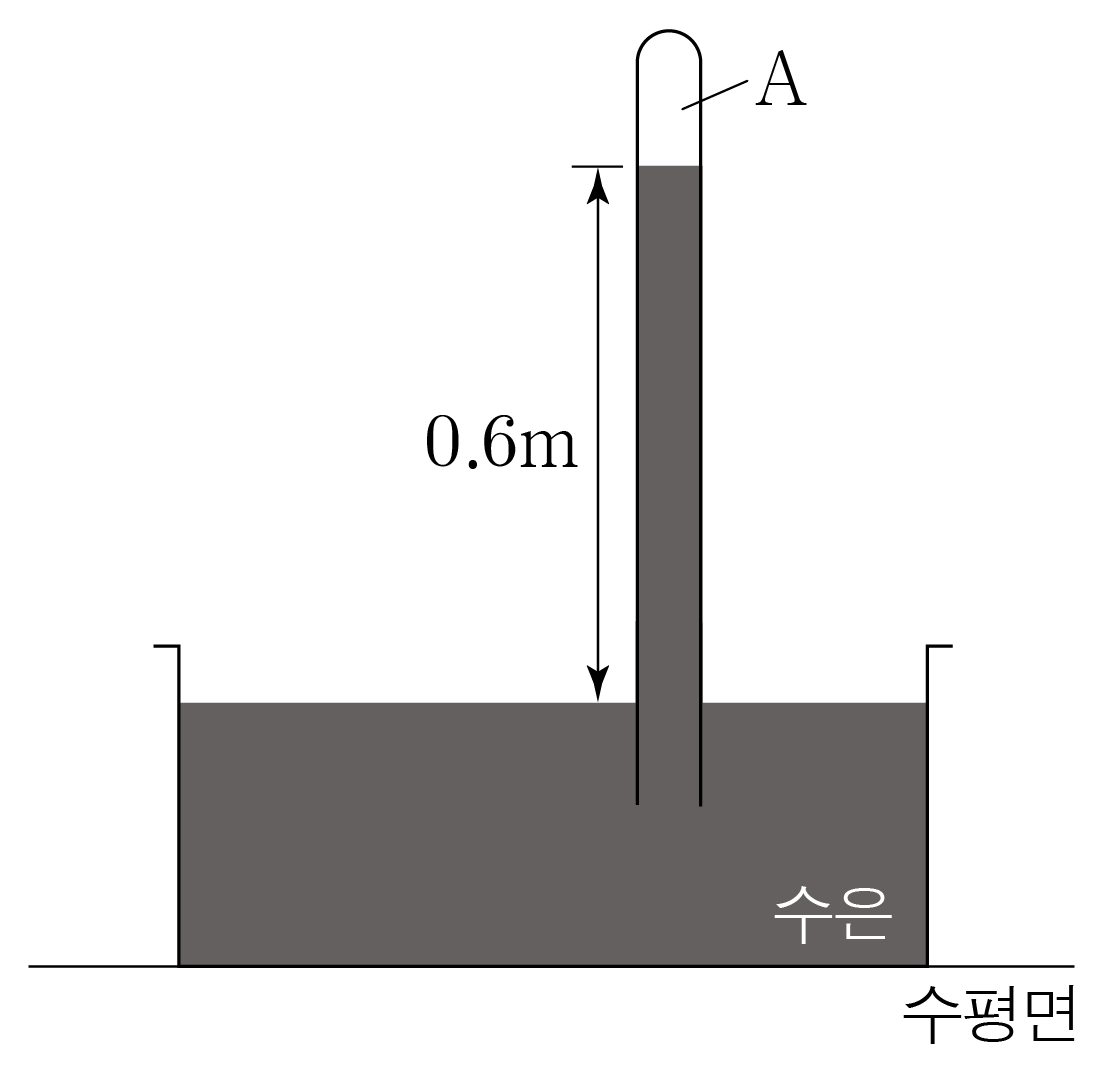
그림은 유리관에 기체 A A 0.6 m 0 . 6 m A A a t m a t m 760 m m H g 7 6 0 m m H g
수은 기둥의 높이는 0.6 m = 600 m m 0 . 6 m = 6 0 0 m m 600 m m H g 6 0 0 m m H g
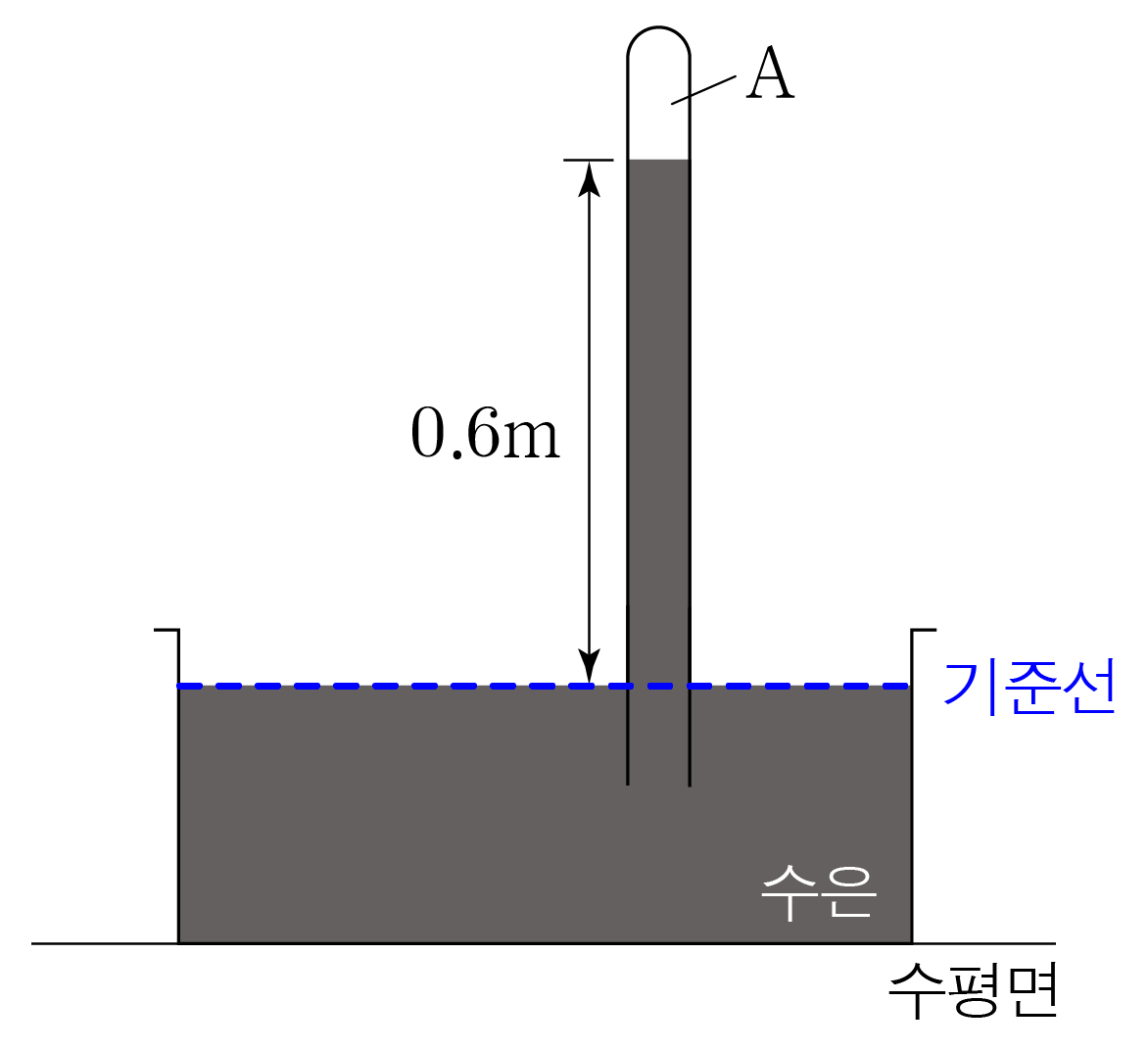
위 그림의 기준선에서 수조 내 수은의 표면과 기둥 안 지점의 압력은 같으므로 A A P A P A 760 m m H g = 600 m m H g + P A , 7 6 0 m m H g = 6 0 0 m m H g + P A , P A = 160 m m H g P A = 1 6 0 m m H g
이때 1 a t m = 760 m m H g , 1 a t m = 7 6 0 m m H g , 1 m m H g = 1 760 a t m 1 m m H g = 7 6 0 1 a t m P A = 160 m m H g = 160 × 1 760 a t m = 4 19 a t m P A = 1 6 0 m m H g = 1 6 0 × 7 6 0 1 a t m = 1 9 4 a t m
1번 문항 정답 및 해설 보기
정답: $3$
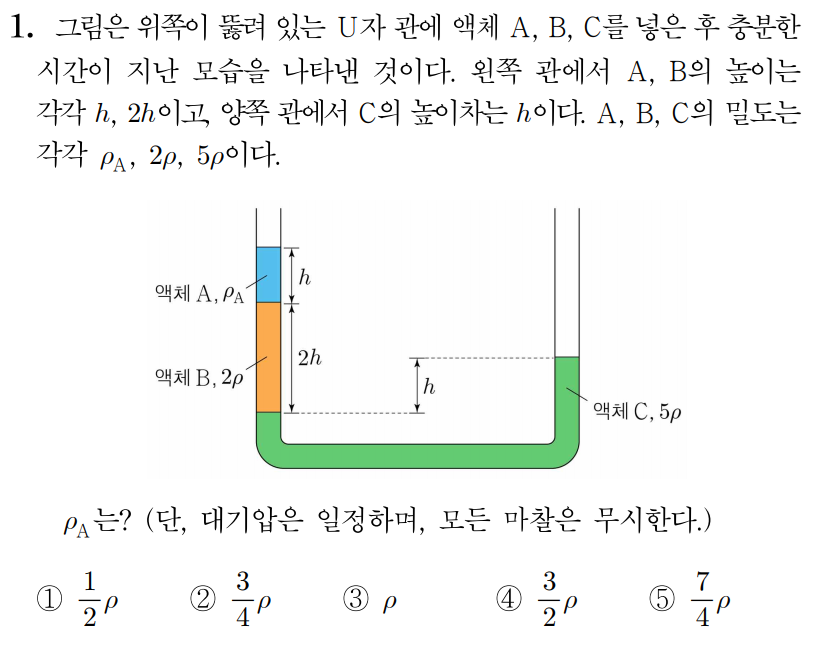
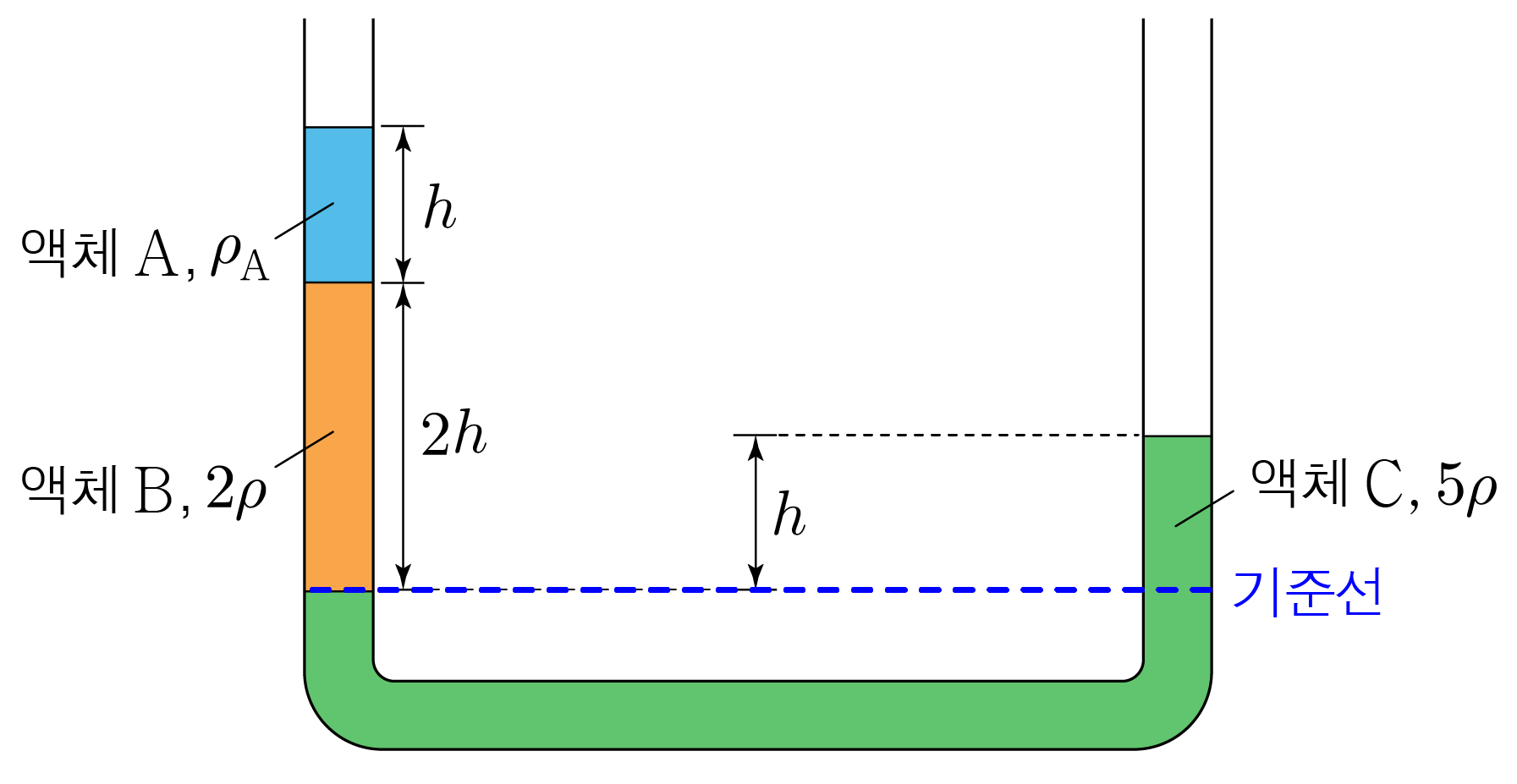
위 그림의 기준선에서 양쪽 관의 압력은 같으므로 중력 가속도를 g g P 0 P 0 P 0 + ρ A g h + 2 ρ g × 2 h = P 0 + 5 ρ g × h , P 0 + ρ A g h + 2 ρ g × 2 h = P 0 + 5 ρ g × h , ρ A g h + 2 ρ g × 2 h = 5 ρ g h , ρ A g h + 2 ρ g × 2 h = 5 ρ g h , ρ A g h + 4 ρ g h = 5 ρ g h , ρ A g h + 4 ρ g h = 5 ρ g h , ρ A g h = ρ g h , ρ A g h = ρ g h , ρ A = ρ ρ A = ρ
따라서 정답은 3 3
2번 문항 정답 및 해설 보기
정답: $4$
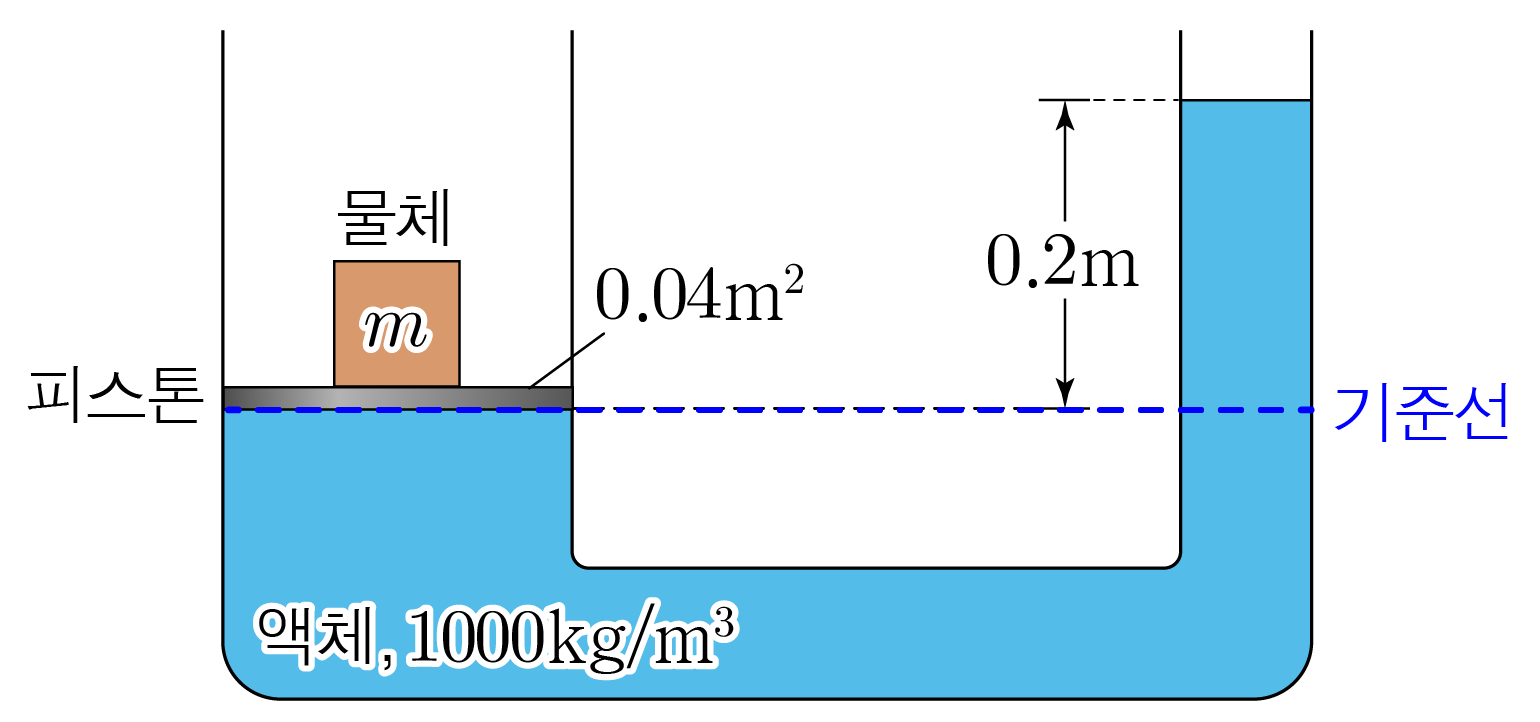
위 그림의 기준선에서 양쪽 관의 압력은 같다.
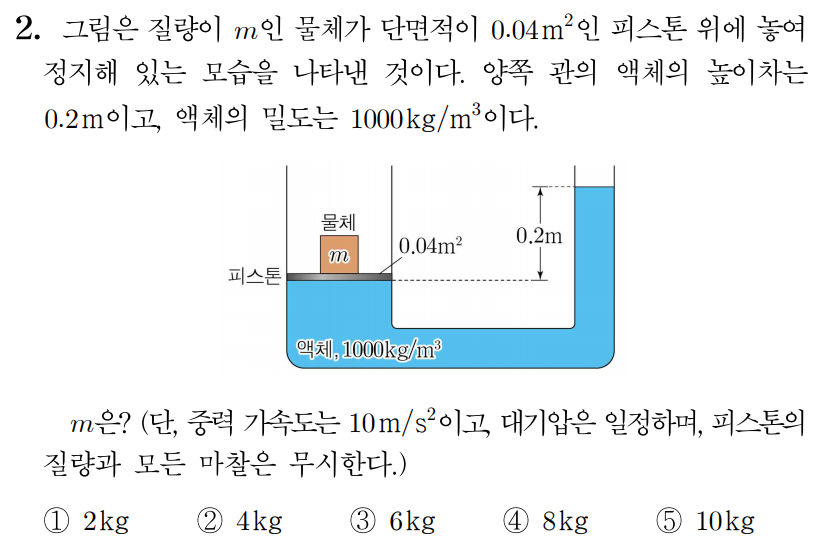
1. 1 . m m 10 m / s 2 1 0 m / s 2 m × 10 m / s 2 m × 1 0 m / s 2 P 0 P 0 P 0 + m × 10 m / s 2 0.04 m 2 P 0 + 0 . 0 4 m 2 m × 1 0 m / s 2
2. 2 . 1000 k g / m 3 1 0 0 0 k g / m 3 10 m / s 2 1 0 m / s 2 0.2 m 0 . 2 m P P P = P 0 + 1000 k g / m 3 × 10 m / s 2 × 0.2 m , P = P 0 + 1 0 0 0 k g / m 3 × 1 0 m / s 2 × 0 . 2 m , P = P 0 + 1000 k g / m 3 × 10 N / k g × 0.2 m , P = P 0 + 1 0 0 0 k g / m 3 × 1 0 N / k g × 0 . 2 m , P = P 0 + 10000 N / m 3 × 0.2 m , P = P 0 + 1 0 0 0 0 N / m 3 × 0 . 2 m , P = P 0 + 2000 N / m 2 P = P 0 + 2 0 0 0 N / m 2
3. 3 . P 0 + m × 10 N 0.04 k g ⋅ m 2 = P 0 + 2000 N / m 2 , P 0 + 0 . 0 4 k g ⋅ m 2 m × 1 0 N = P 0 + 2 0 0 0 N / m 2 , m × 10 N 0.04 k g ⋅ m 2 = 2000 N / m 2 , 0 . 0 4 k g ⋅ m 2 m × 1 0 N = 2 0 0 0 N / m 2 , m × 10 0.04 k g = 2000 , 0 . 0 4 k g m × 1 0 = 2 0 0 0 , 250 m 1 k g = 2000 , 1 k g 2 5 0 m = 2 0 0 0 , m 1 k g = 8 , 1 k g m = 8 , m = 8 k g m = 8 k g
따라서 정답은 4 4