분석하고자 하는 대상 전체를 하나로 묶어서 부른 것이다.
물체나 계의 질량이 한 점에 모여 있다고 볼 수 있는 점이다.
한 물질로 이루어진 막대와 같이 밀도가 균일하고 좌우대칭인 물체의 질량 중심은 물체의 중앙에 위치한다.
직선 상에 물체가 총 n개 있고, i번째 물체의 질량을 mi, 기준점(원점)으로부터 i번째 물체까지의 거리를 ri라 할 때,
이 물체들로 이루어진 계의 질량 중심의 위치는 i=1∑nmii=1∑nmiri이다.
- 밀도가 균일하고 좌우대칭인 물체의 질량 중심 구하기:
그림은 x 축에 밀도가 균일하고 길이가 10m인 막대가 놓여 있는 것을 나타낸 것이다.
막대의 질량 중심의 위치를 구해 보자. (단, 막대의 두께와 폭은 무시한다.)
밀도가 균일하고 좌우대칭인 물체의 질량 중심은 물체의 중앙에 위치하므로 질량 중심의 위치는 x=5m이다.
그림은 x 축에 물체 A, B, C가 놓여 있는 것을 나타낸 것이다. A, B, C의 질량은 각각 1kg, 3kg, 2kg이다.
A, B, C로 이루어진 계의 질량 중심의 위치를 구해 보자. (단, 물체의 크기는 무시한다.)
어느 계에 물체가 총 n개 있고, i번째 물체의 질량을 mi, 기준점(원점)으로부터 i번째 물체까지의 거리를 ri라 할 때,
이 계의 질량 중심의 위치는 i=1∑nmii=1∑nmiri이다.
물체가 총 3개이므로 n=3이고, A, B, C를 각각 1, 2, 3번째 물체라 하면
m1=1kg, m2=3kg, m3=2kg이다.
따라서 i=1∑nmi=i=1∑3mi=m1+m2+m3=1kg+3kg+2kg=6kg이다.
x=0을 기준점이라 하면 r1=2m, r2=4m, r3=8m이다.
그러므로 i=1∑nmiri=i=1∑3miri,
i=1∑nmiri=m1r1+m2r2+m3r3,
i=1∑nmiri=(1kg×2m)+(3kg×4m)+(2kg×8m),
i=1∑nmiri=2kg⋅m+12kg⋅m+16kg⋅m,
i=1∑nmiri=30kg⋅m이다.
따라서 i=1∑nmii=1∑nmiri=i=1∑3mii=1∑3miri=6kg30kg⋅m=5m이므로 계의 질량 중심의 위치는 x=5m이다.
정답: $2$
어느 계에 물체가 총 n개 있고, i번째 물체의 질량을 mi, 기준점(원점)으로부터 i번째 물체까지의 거리를 ri라 할 때,
이 계의 질량 중심의 위치는 i=1∑nmii=1∑nmiri이다.
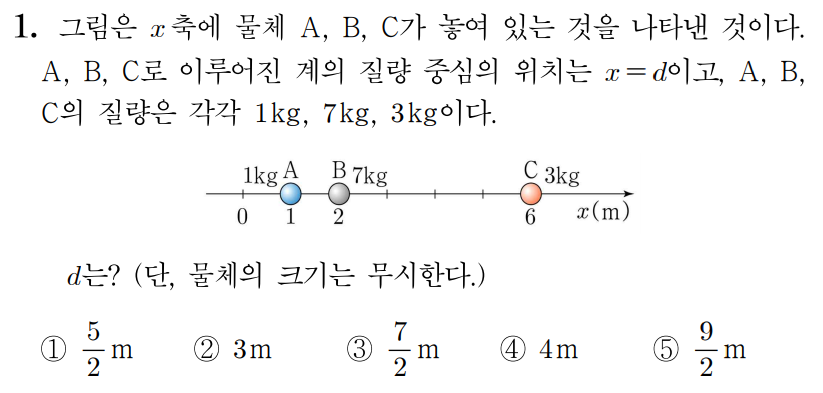
물체가 총 3개이므로 n=3이고, A, B, C를 각각 1, 2, 3번째 물체라 하면
m1=1kg, m2=7kg, m3=3kg이다.
따라서 i=1∑nmi=i=1∑3mi=m1+m2+m3=1kg+7kg+3kg=11kg이다.
x=0을 기준점이라 하면 r1=1m, r2=2m, r3=6m이다.
그러므로 i=1∑nmiri=i=1∑3miri,
i=1∑nmiri=m1r1+m2r2+m3r3,
i=1∑nmiri=(1kg×1m)+(7kg×2m)+(3kg×6m),
i=1∑nmiri=1kg⋅m+14kg⋅m+18kg⋅m,
i=1∑nmiri=33kg⋅m이다.
i=1∑nmii=1∑nmiri=i=1∑3mii=1∑3miri=11kg33kg⋅m=3m이므로 계의 질량 중심의 위치는 x=3m이다.
따라서 정답은 2번이다.
정답: $4$
어느 계에 물체가 총 n개 있고, i번째 물체의 질량을 mi, 기준점(원점)으로부터 i번째 물체까지의 거리를 ri라 할 때,
이 계의 질량 중심의 위치는 i=1∑nmii=1∑nmiri이다.
물체가 총 3개이므로 n=3이고, A, B, C를 각각 1, 2, 3번째 물체라 하면
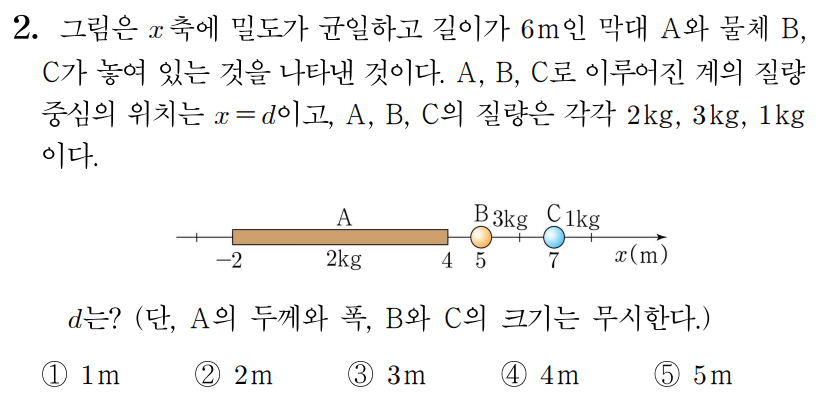
m1=2kg, m2=3kg, m3=1kg이다.
따라서 i=1∑nmi=i=1∑3mi=m1+m2+m3=2kg+3kg+1kg=6kg이다.
x=0을 기준점이라 하면 밀도가 균일하고 좌우대칭인 물체의 질량 중심은 물체의 중앙이므로
r1=1m이고, r2=5m, r3=7m이다.
그러므로 i=1∑nmiri=i=1∑3miri,
i=1∑nmiri=m1r1+m2r2+m3r3,
i=1∑nmiri=(2kg×1m)+(3kg×5m)+(1kg×7m),
i=1∑nmiri=2kg⋅m+15kg⋅m+7kg⋅m,
i=1∑nmiri=24kg⋅m이다.
i=1∑nmii=1∑nmiri=i=1∑3mii=1∑3miri=6kg24kg⋅m=4m이므로 계의 질량 중심의 위치는 x=4m이다.
따라서 정답은 4번이다.