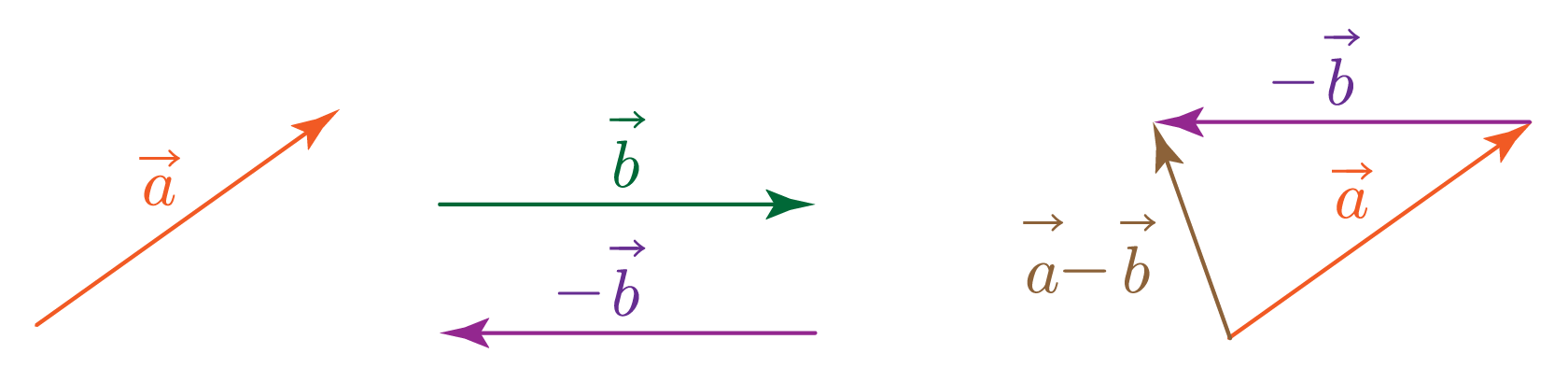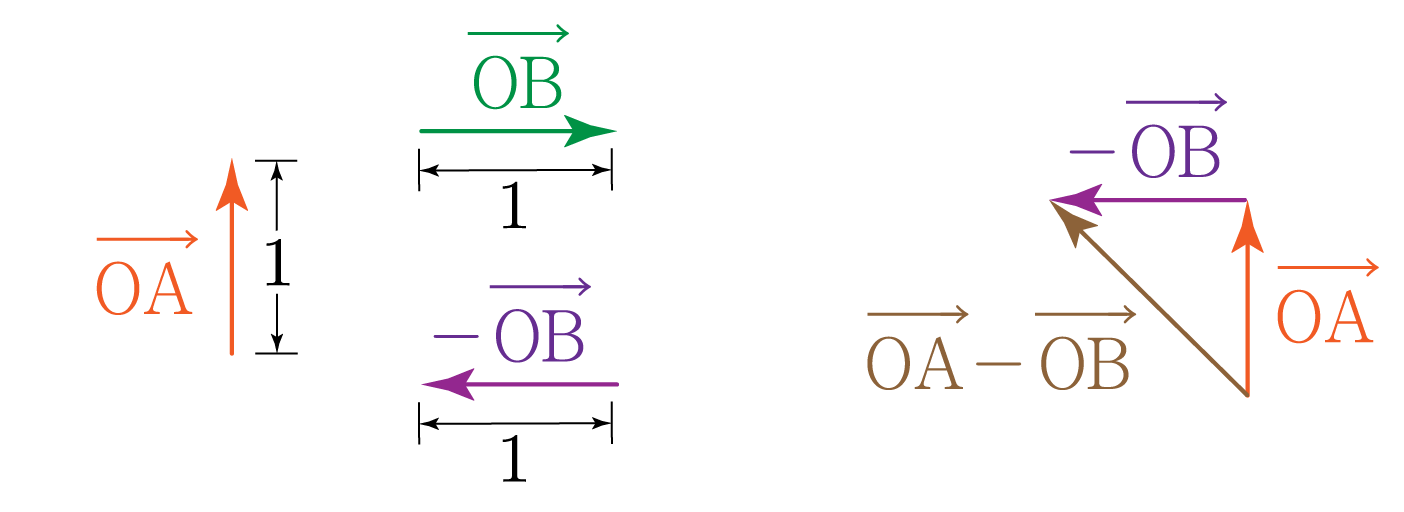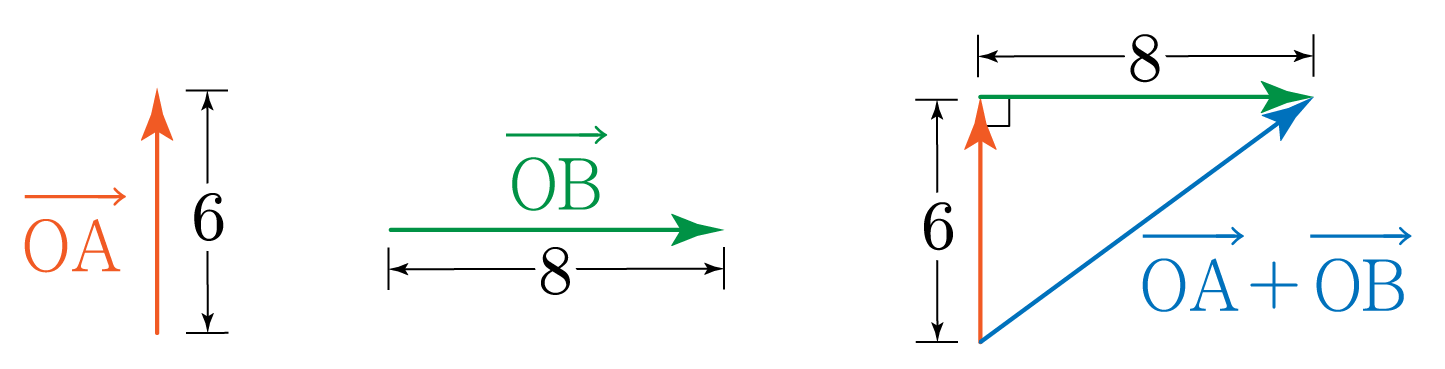크기와 방향을 함께 가진 것을 벡터, 크기만 가진 것을 스칼라라고 한다.
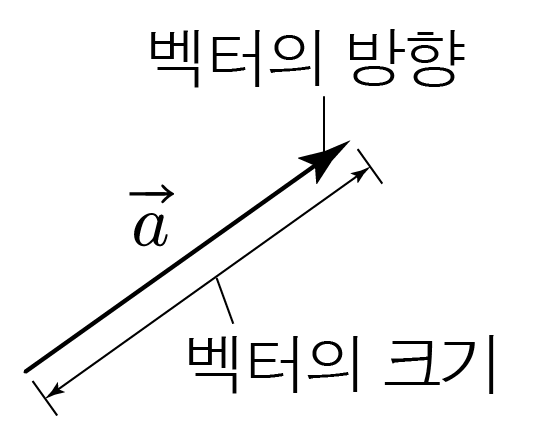
벡터는 그림으로 나타낼 때 화살표로 나타내고, 화살표의 길이는 벡터의 크기를, 화살표의 방향은 벡터의 방향을 의미한다.
벡터를 수식으로 나타낼 때는 a와 같이 진한 글씨인 볼드체나 기호 위에 a처럼 화살표를 그려 나타낸다.
벡터 a의 크기는 ∣a∣와 같이 절댓값을 통해 나타낸다.
수학에서 벡터는 크기와 방향만 같다면 위치에 관계없이 같은 벡터이다.
두 벡터의 크기는 같고 방향만 반대일 때, 부호는 서로 반대이다.
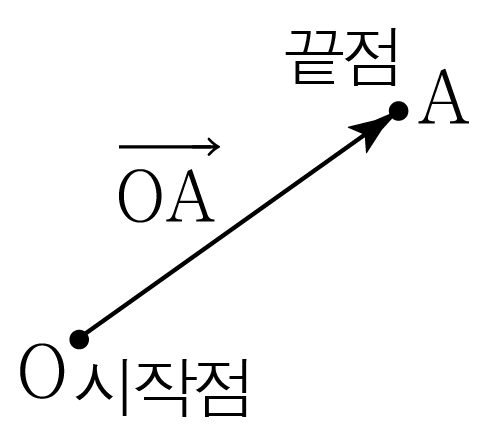
시작점을 O, 끝점을 A로 하는 벡터를 표기할 때는 OA와 같이 나타낸다.
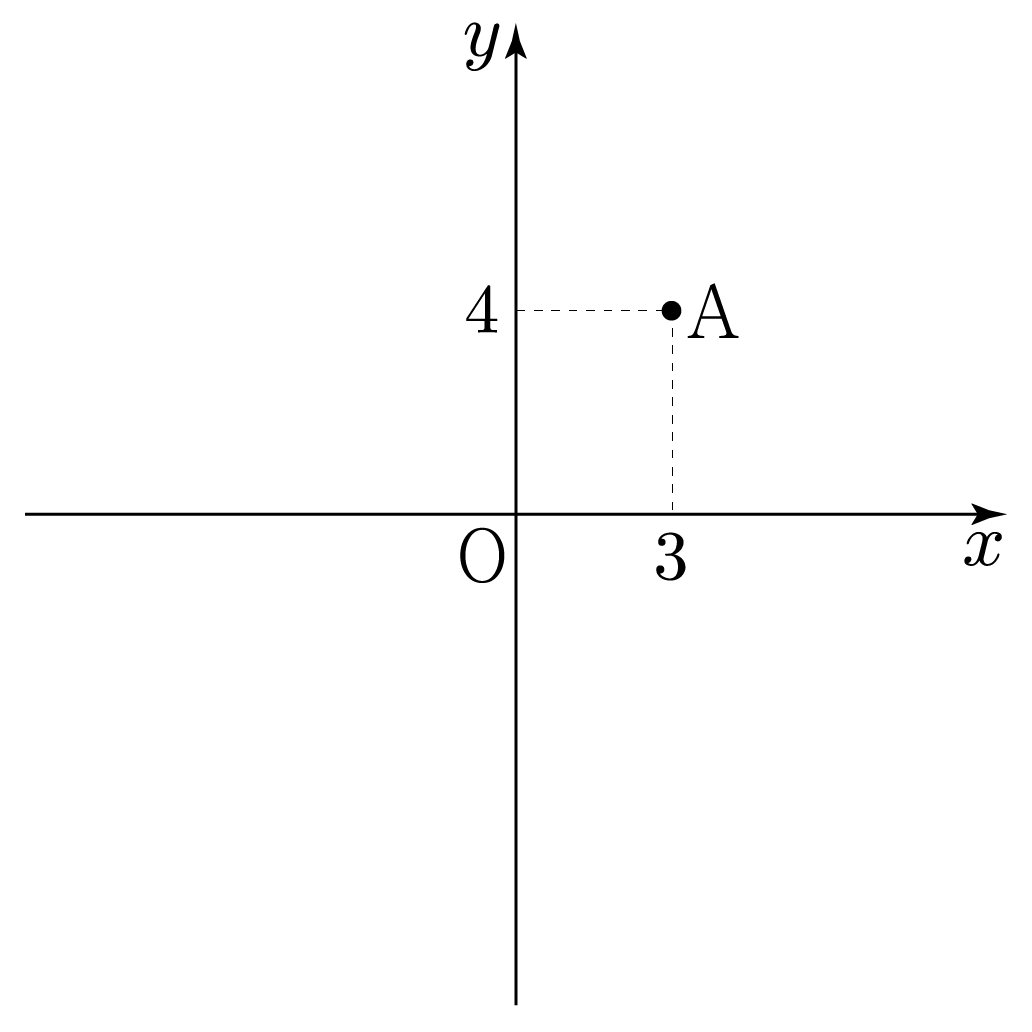
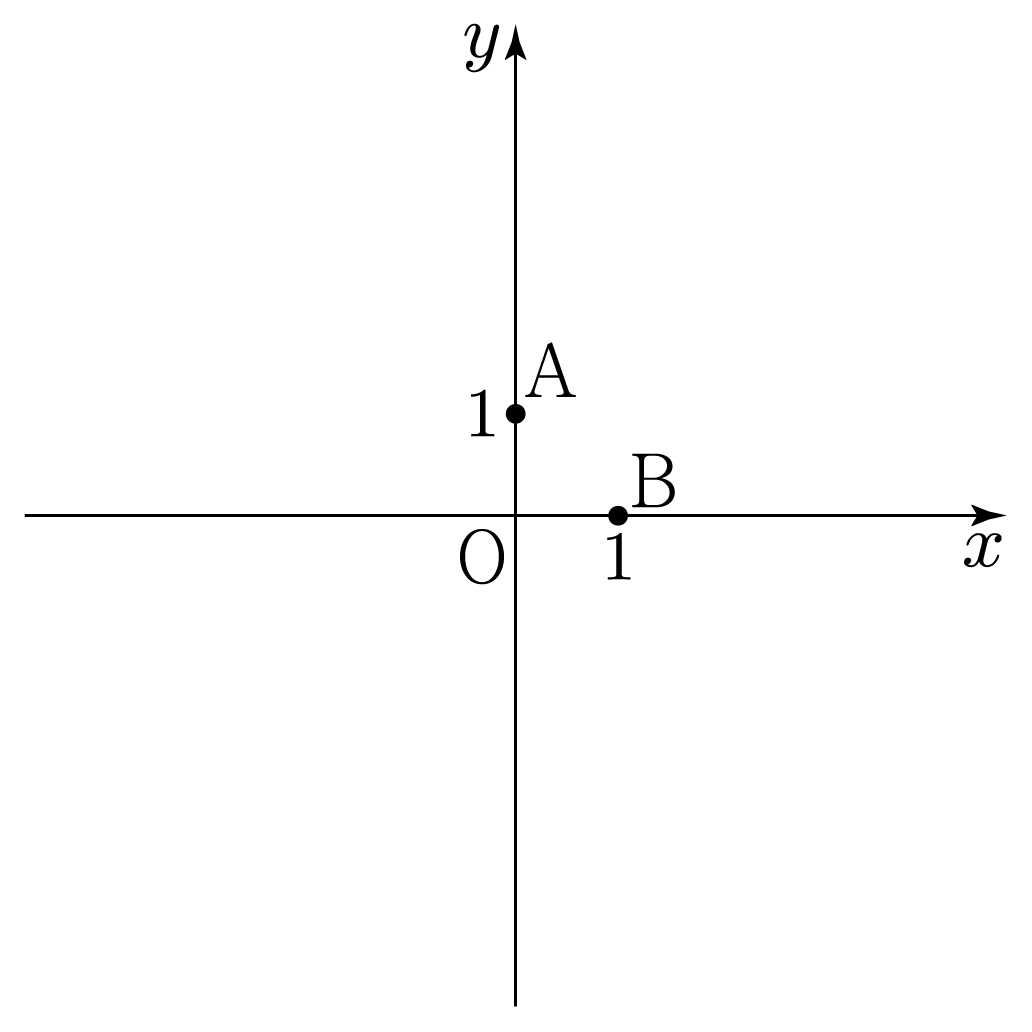
그림과 같이 좌표 평면에 점 A(3,4)가 있다. 이때 OA의 크기를 구해보자.
벡터의 길이는 벡터의 크기를 의미하므로 OA의 길이(OA)를 구하면 된다.
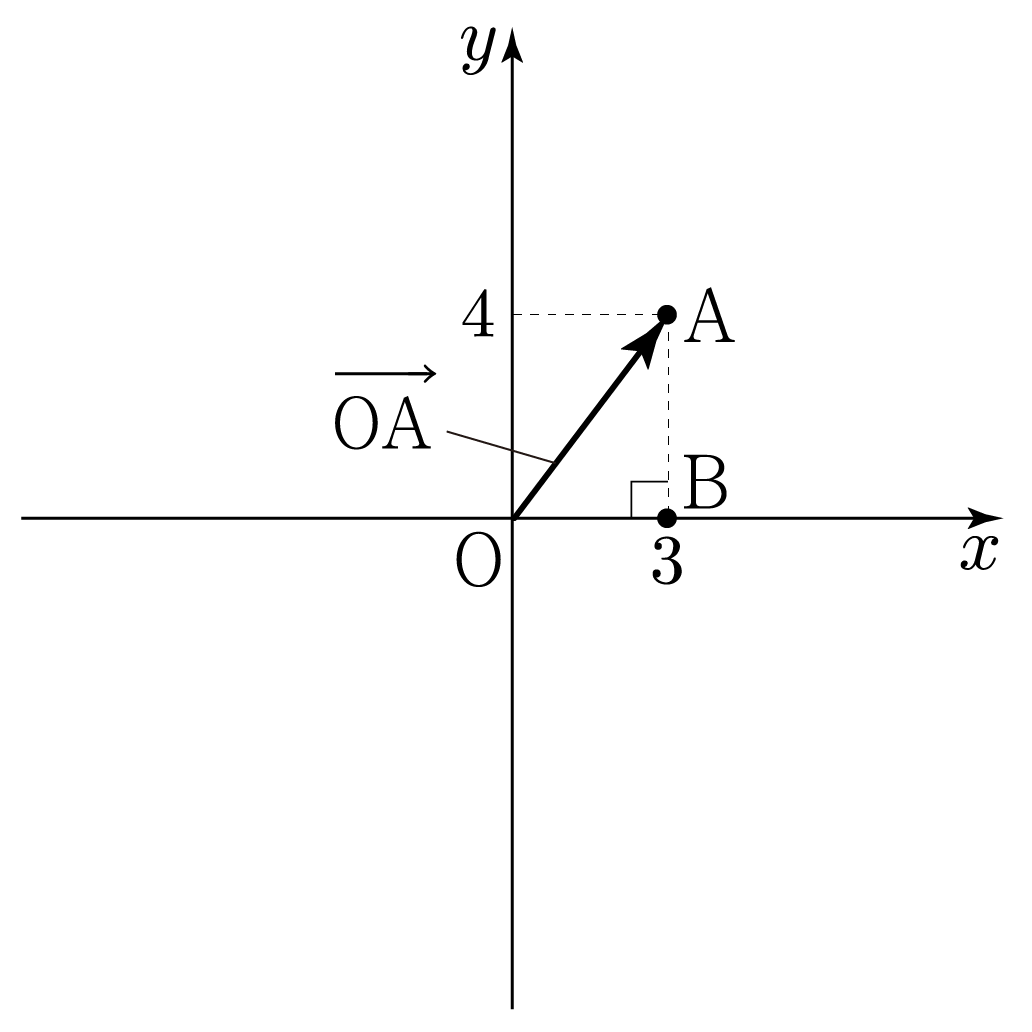
위 그림과 같이 추가로 점 B(3,0)를 그리면 삼각형 ABO(점 A, B, O를 서로 이은 도형)는 직각삼각형이므로 피타고라스 정리를 적용하여 32+42=(OA)2,
9+16=(OA)2,
25=(OA)2,
52=(OA)2,
따라서 OA=5이다.
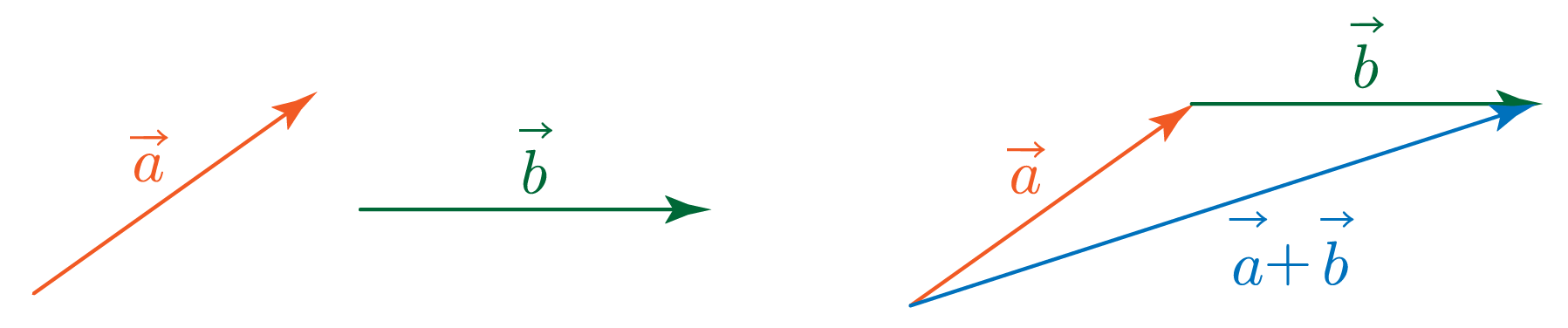
두 벡터 a, b의 합 a+b는 a의 끝에서 b를 출발시켜 삼각형을 만들 때, 시작점에서 끝점까지이다.
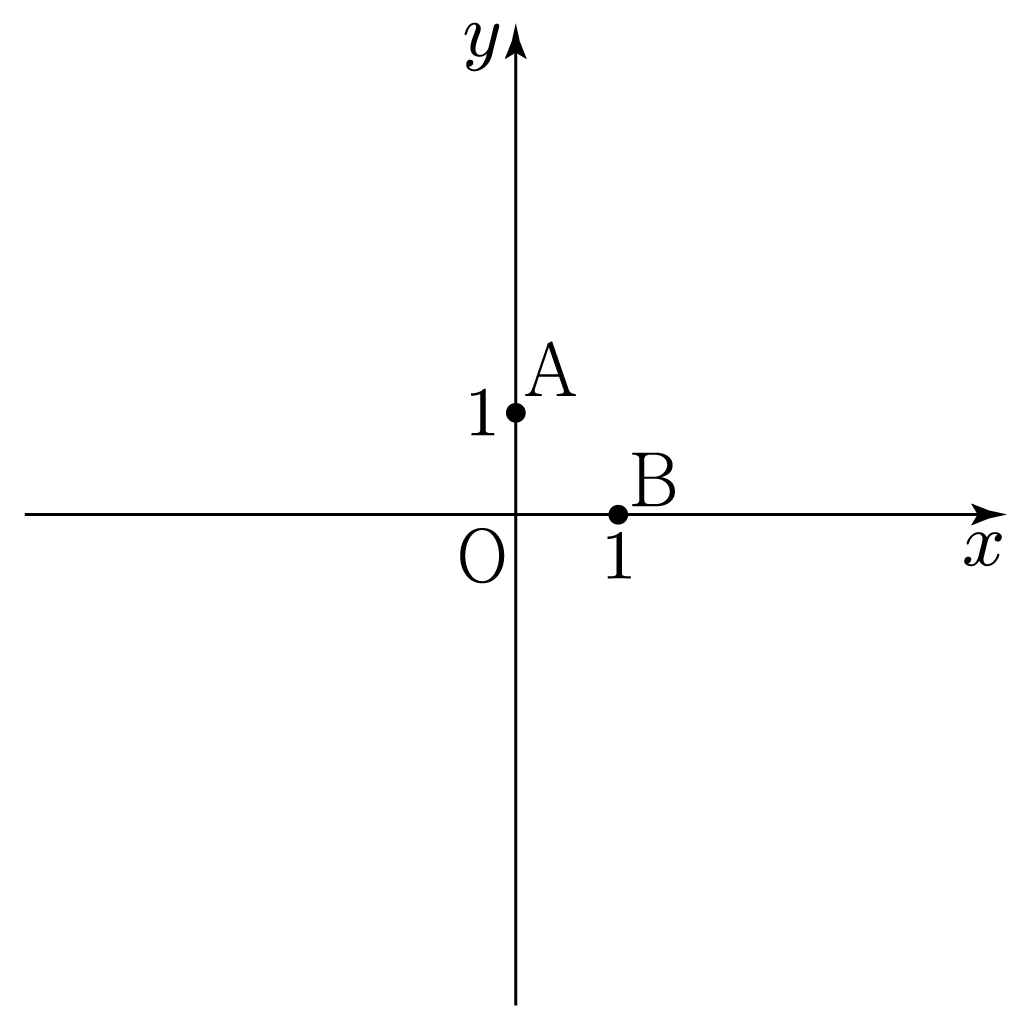
그림과 같이 좌표 평면에 두 점 A(0,1), B(1,0)가 있을 때, OA+OB를 구해보자.
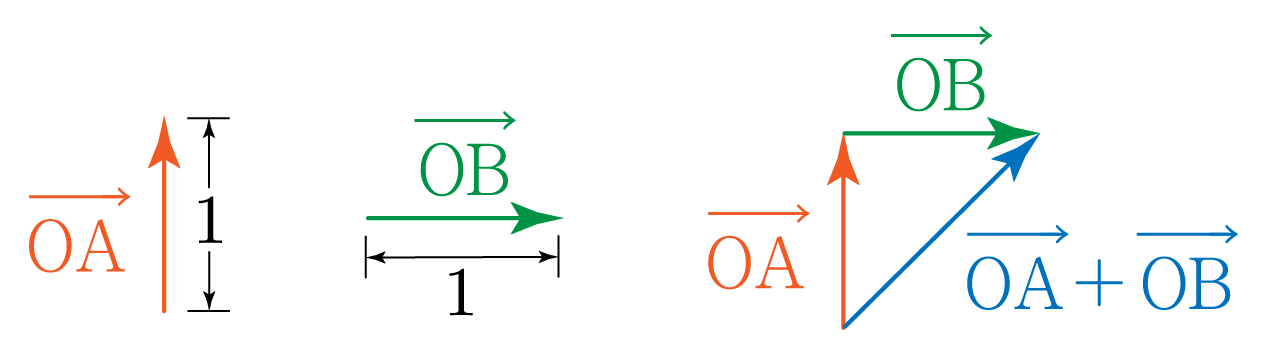
아래 그림과 같이 OA, OB를 그린다.
이후 OA의 끝에서 OB를 출발시켜 삼각형을 만들어 OA+OB를 구한다.
두 벡터 a, b의 차 a−b는 b의 방향만 반대로 바꿔 −b로 만든 후, a와 −b의 합을 구한다.
그림과 같이 좌표 평면에 두 점 A(0,1), B(1,0)가 있을 때, OA−OB를 구해보자.
아래 그림과 같이 OA, −OB를 그린다.
이후 OA의 끝에서 −OB를 출발시켜 삼각형을 만들어 OA−OB를 구한다.
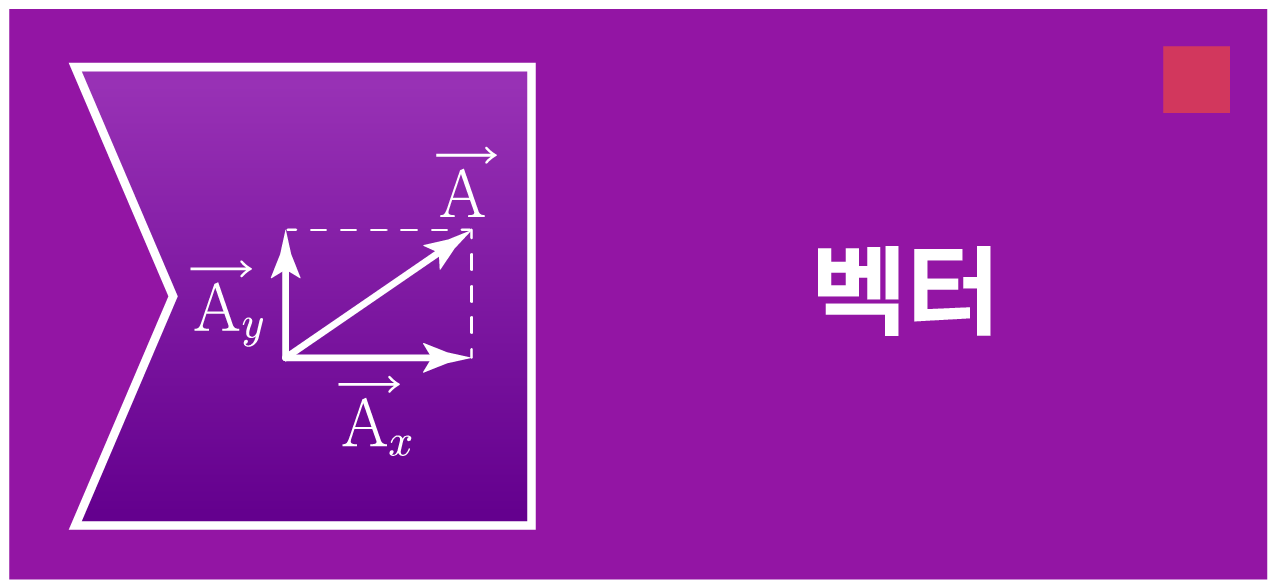
하나의 벡터를 서로 수직인 두 개 이상의 벡터로 분해하는 것이다.
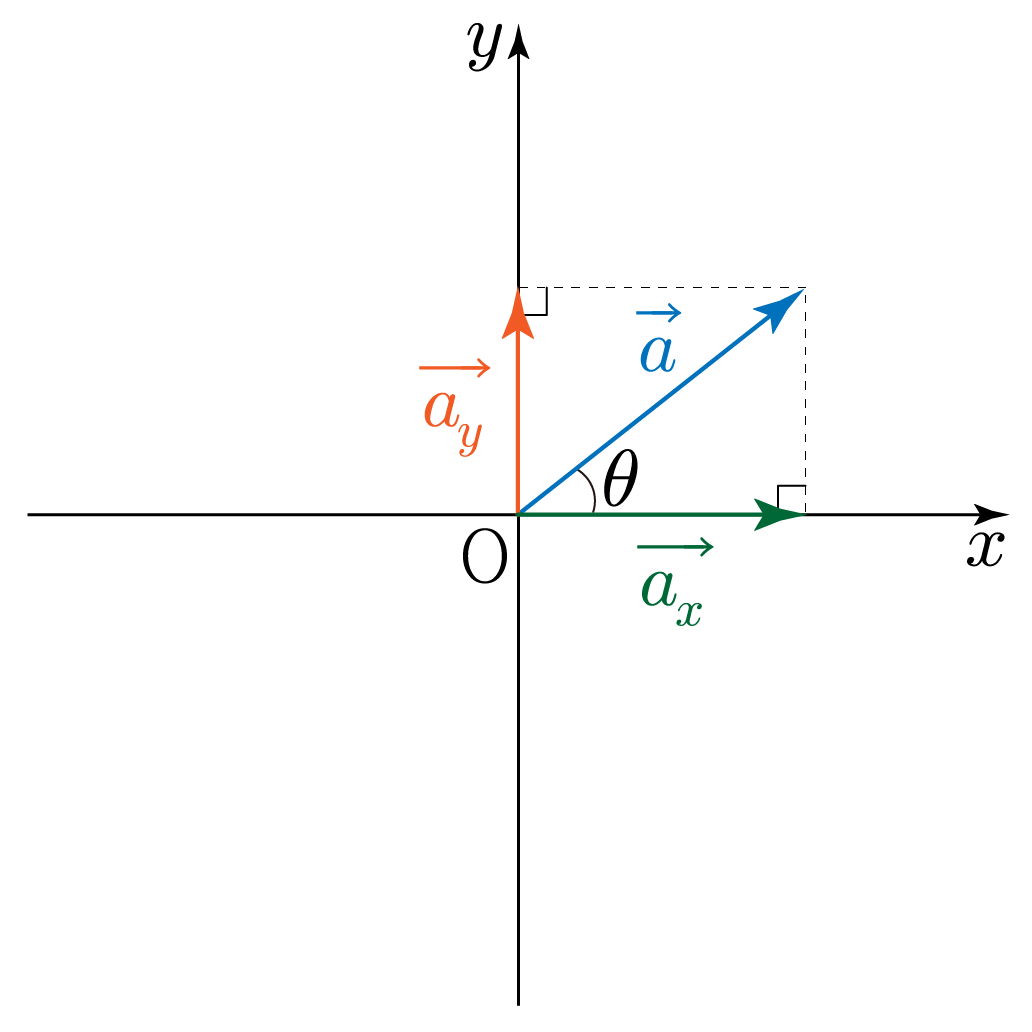
아래 그림과 같이 xy 평면에 벡터 a가 있을 때, x축과 y축에 나란한 벡터 ax, ay로 분해할 수 있다.
ax, ay는 각각 a의 x 성분, a의 y 성분이라고 하며,
삼각비를 통해 ∣ax∣=∣a∣cosθ,∣ay∣=∣a∣sinθ이고,
피타고라스 정리를 통해 ∣ax∣2+∣ay∣2=∣a∣2임을 알 수 있다.
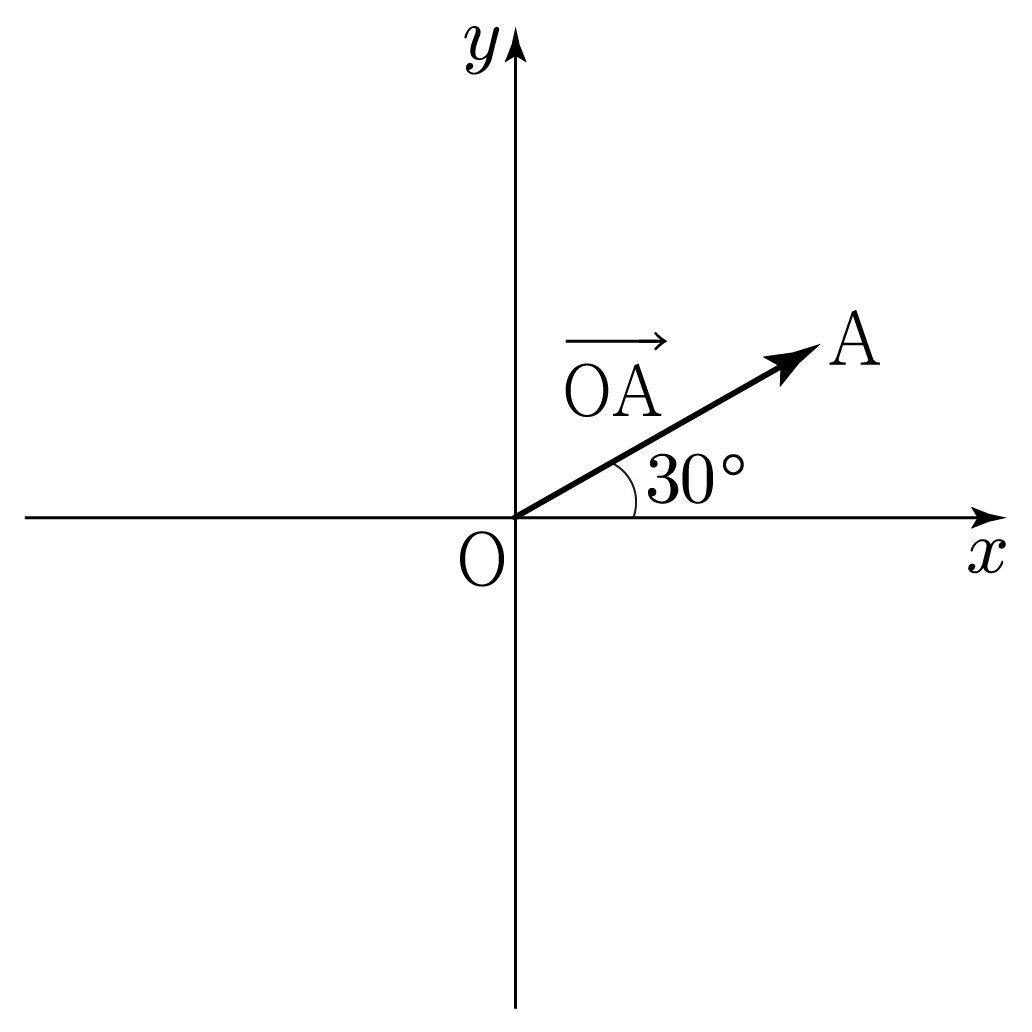
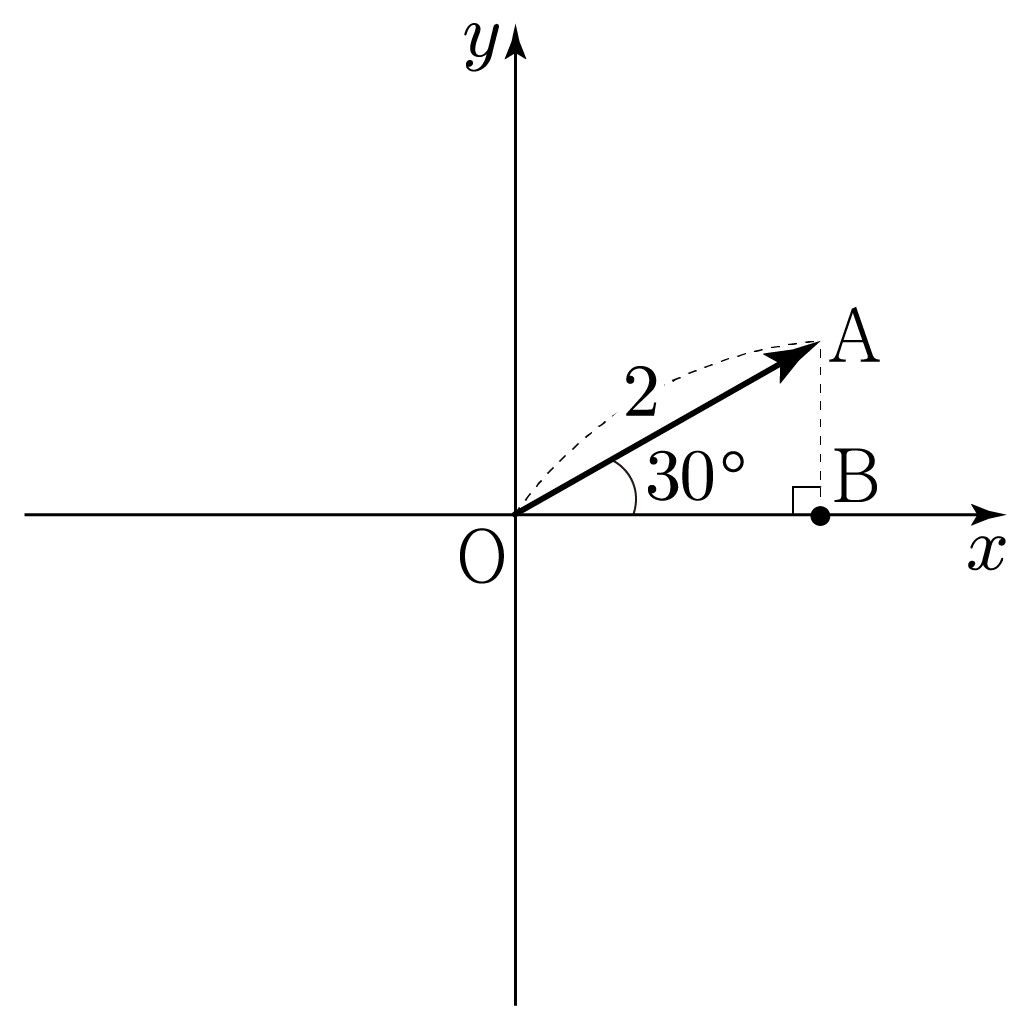
그림과 같이 좌표 평면에 크기가 2인 벡터 OA가 있다. OA와 x축이 이루는 각도가 30∘일 때, OA의 y 성분의 크기를 구해보자.
아래 그림과 같이 x값이 A와 같고 y값이 0인 점 B를 그리면 OA의 y 성분의 크기는 AB의 길이와 같다.
삼각형 AOB는 OA가 빗변, ∠AOB에 대하여 AB가 대변이므로
sin30∘=빗변대변=OAAB=2AB인데, 특수각 30∘에서 sin30∘=21이므로
sin30∘=2AB=21,
AB=1이다.
따라서 OA의 y 성분의 크기는 1이다.
정답: $4$
아래 그림과 같이 OA, OB를 그린다.
이후 OA의 끝에서 OB를 출발시켜 삼각형을 만들어 OA+OB를 구한다.
OA, OB는 수직을 이루므로 피타고라스 정리를 활용하면,
OA+OB의 크기를 x라 할 때,
62+82=x2,
36+64=x2,
100=x2,
102=x2,
x=10이다.
따라서 정답은 4번이다.

정답: $2$
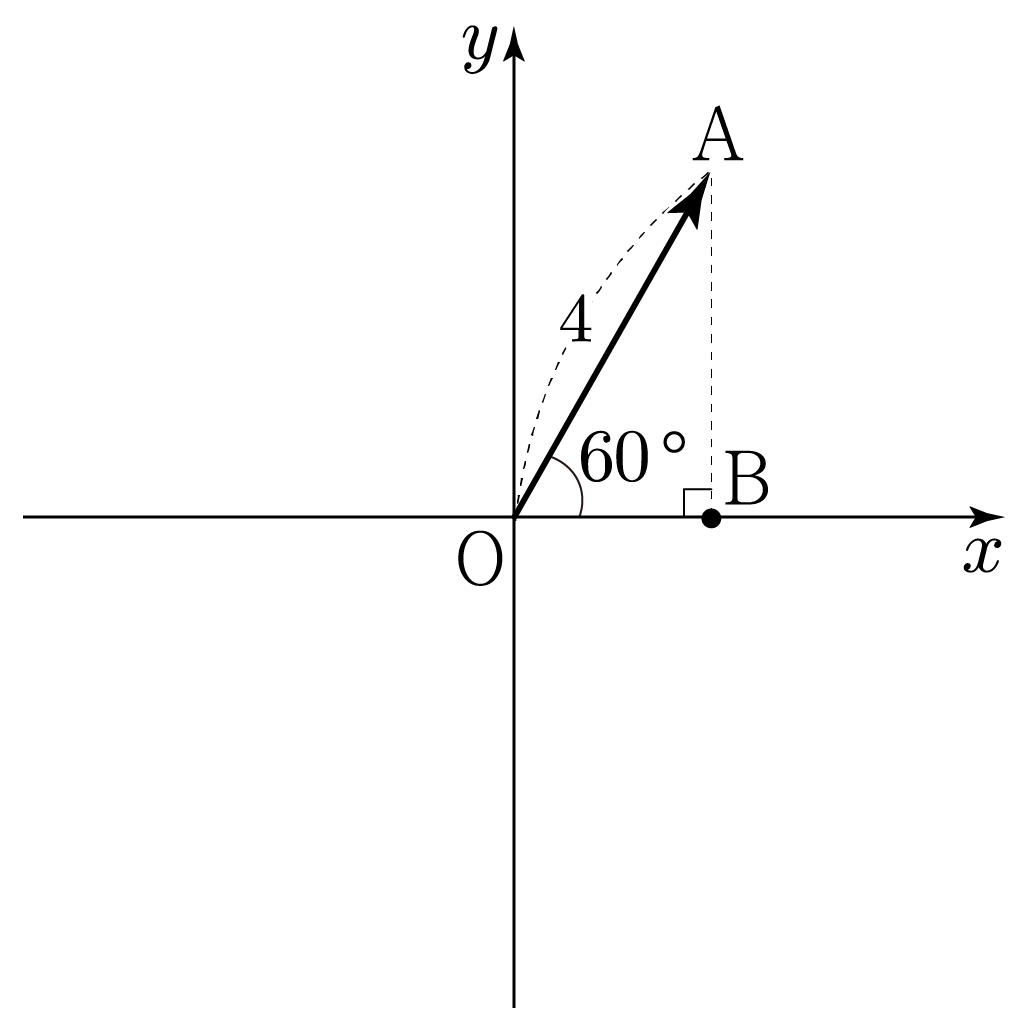
아래 그림과 같이 x값이 A와 같고 y값이 0인 점 B를 그리면 OA의 x 성분의 크기는 OB의 길이와 같다.
삼각형 AOB는 OA가 빗변, ∠AOB에 대하여 AB가 대변, OB가 인접변에 해당하므로
cos60∘=빗변인접변=OAOB=4OB인데, 특수각 60∘에서 cos60∘=21이므로
cos60∘=4OB=21,
OB=2이다.
그러므로 OA의 x 성분의 크기는 2이다.
따러서 정답은 2번이다.