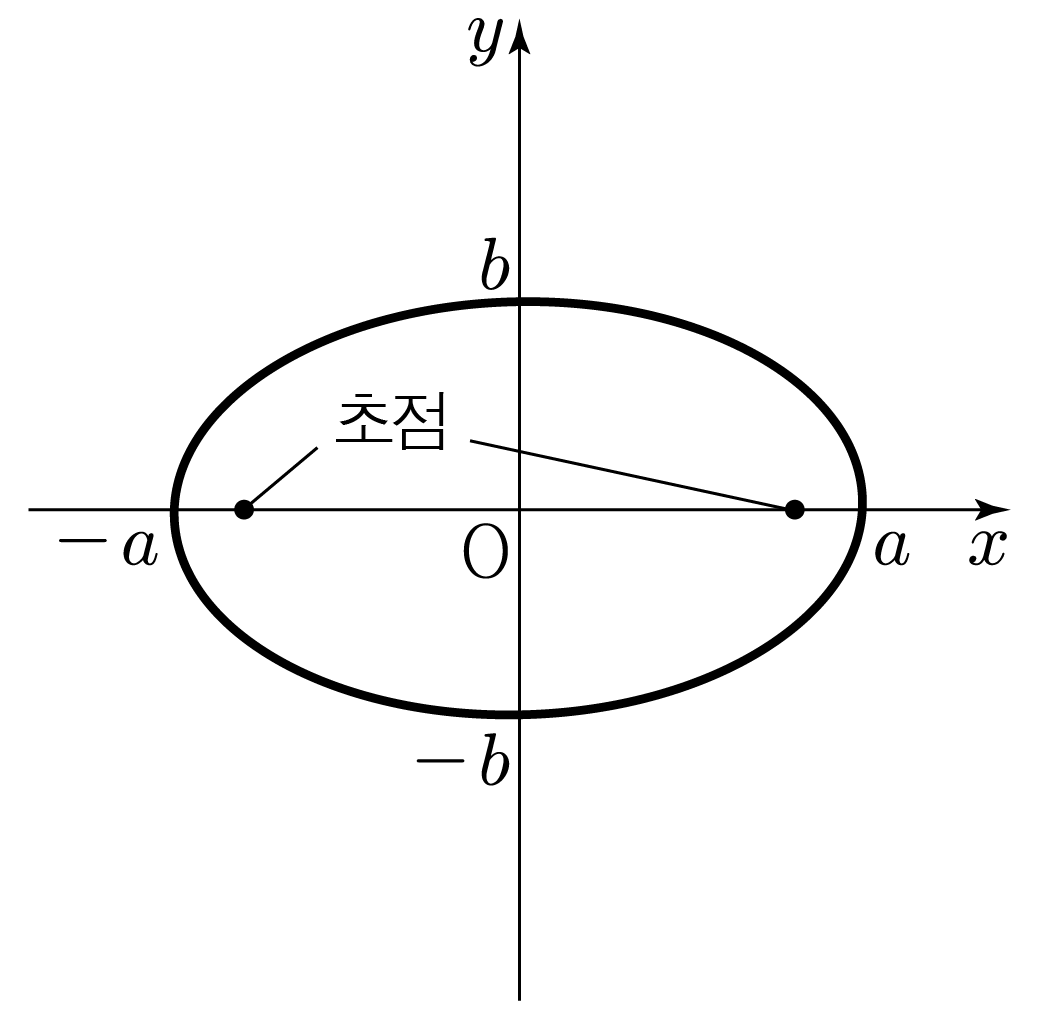
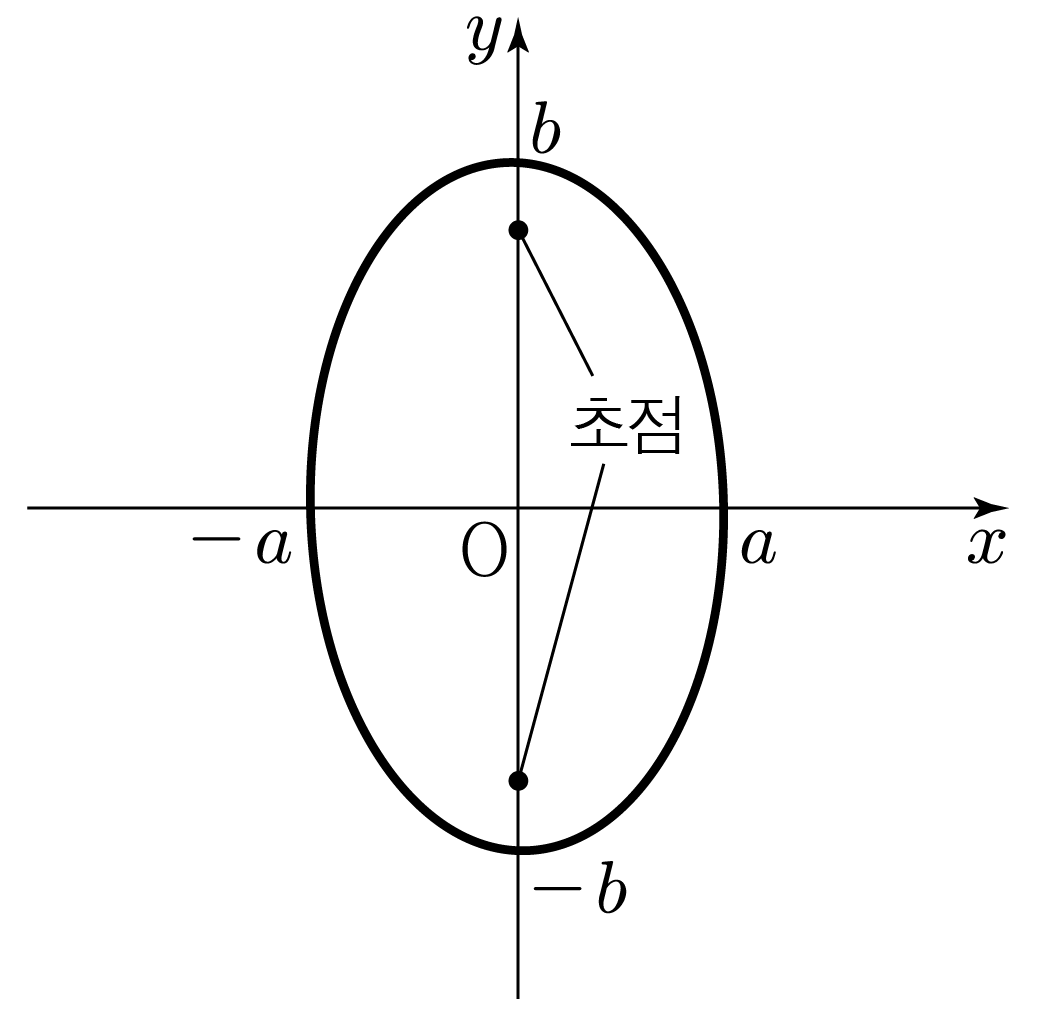
두 점으로부터 거리의 합이 같은 점들로 이루어진 도형이며, 여기서 두 점은 타원의 초점이라 한다.
타원의 중심이 원점에 있을 때 타원의 방정식은 a2x2+b2y2=1이다.
a는 x축 방향의 반지름, b는 y축 방향의 반지름이다.
1. x축으로 긴 타원이며, 초점은 x축에 위치한다.
2. 두 초점으로부터 타원의 어느 지점까지의 거리의 합은 2a이다.
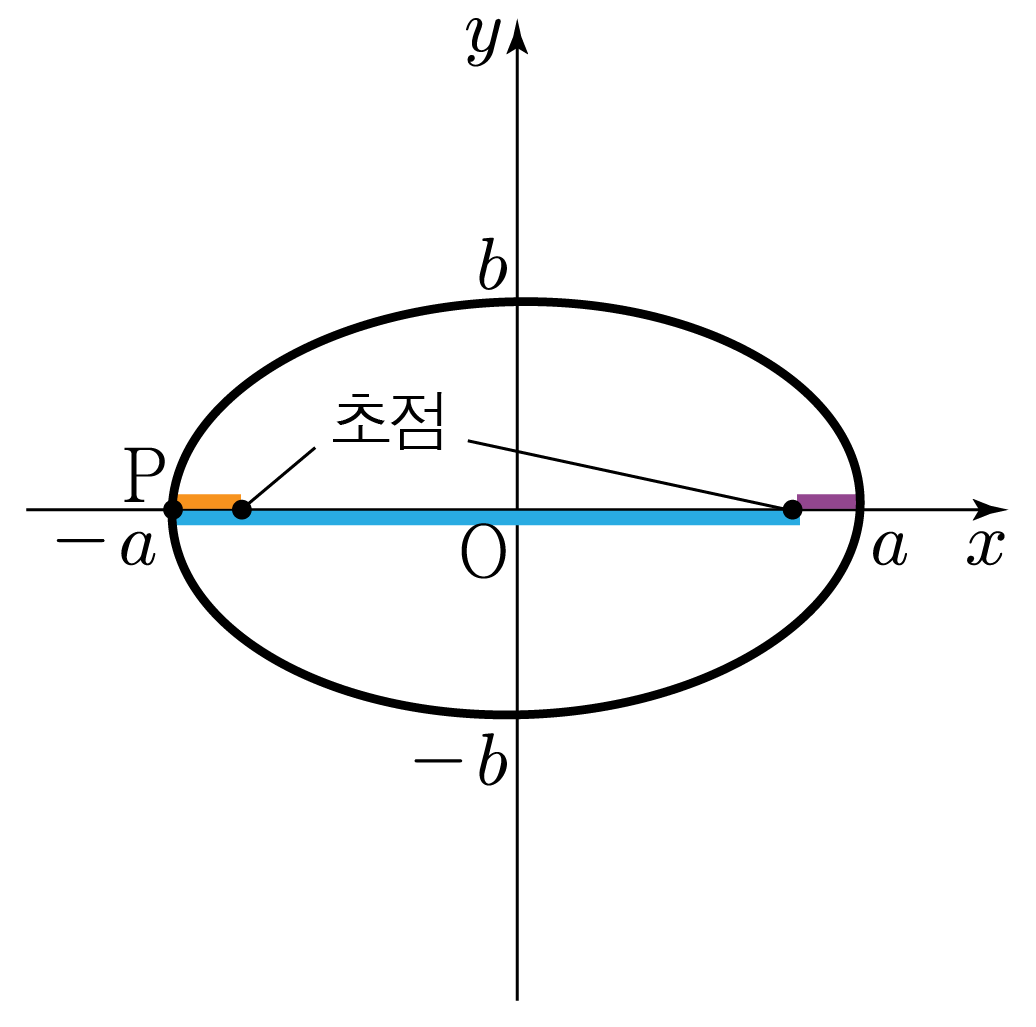
아래 그림과 같이 타원 위의 지점 (−a,0)에 점 P가 있다고 해보자.
P와 왼쪽에 위치한 초점 사이의 거리는 주황색 선의 길이에 해당하고,
P와 오른쪽에 위치한 초점 사이의 거리는 파란색 선의 길이에 해당한다.
이때, 주황색 선의 길이는 보라색 선의 길이와 같다.
그러므로 두 초점으로부터 타원의 어느 지점까지의 거리의 합은 보라색 선의 길이와 파란색 선의 길이의 합인 2a임을 알 수 있다.
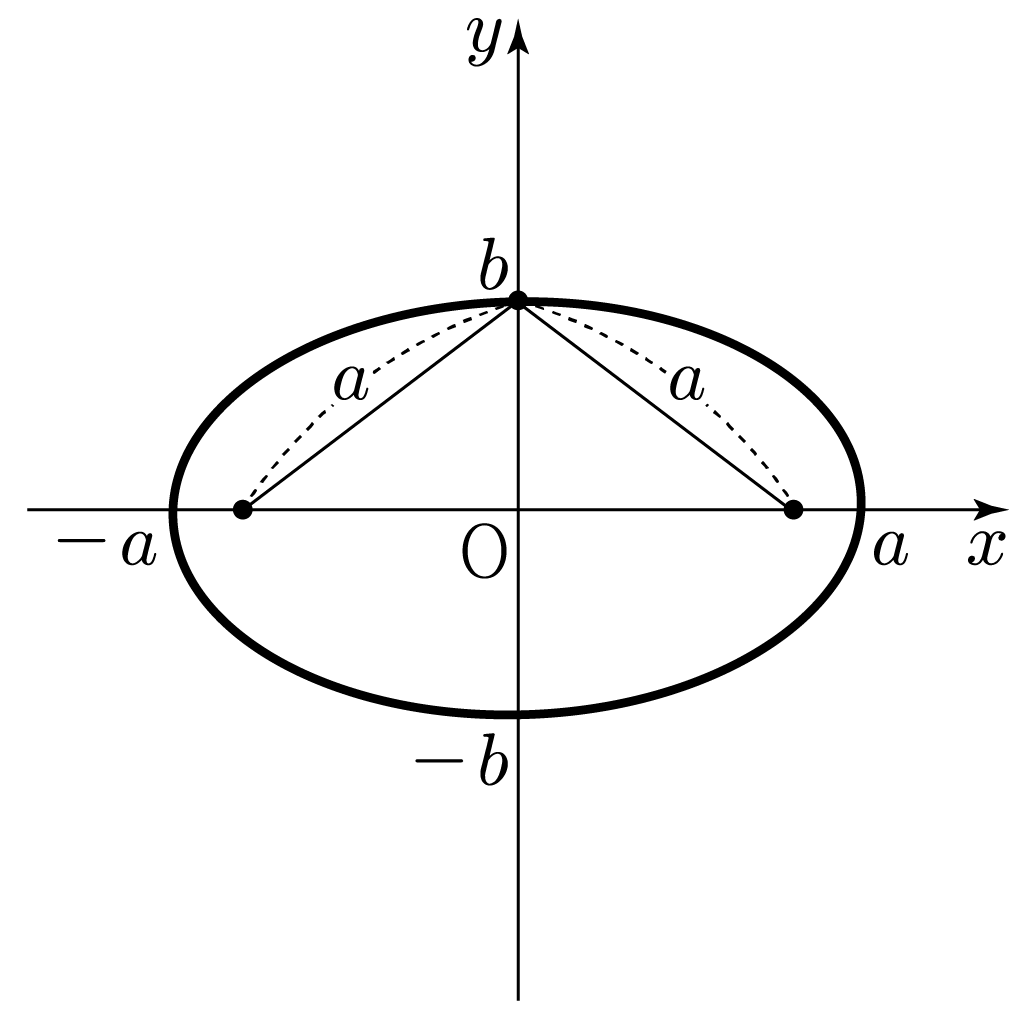
두 초점으로부터 타원의 어느 지점까지의 거리의 합이 2a이므로
아래 그림과 같이 타원 위의 지점 (0,b)와 각 초점 사이의 거리는 a로 같다.
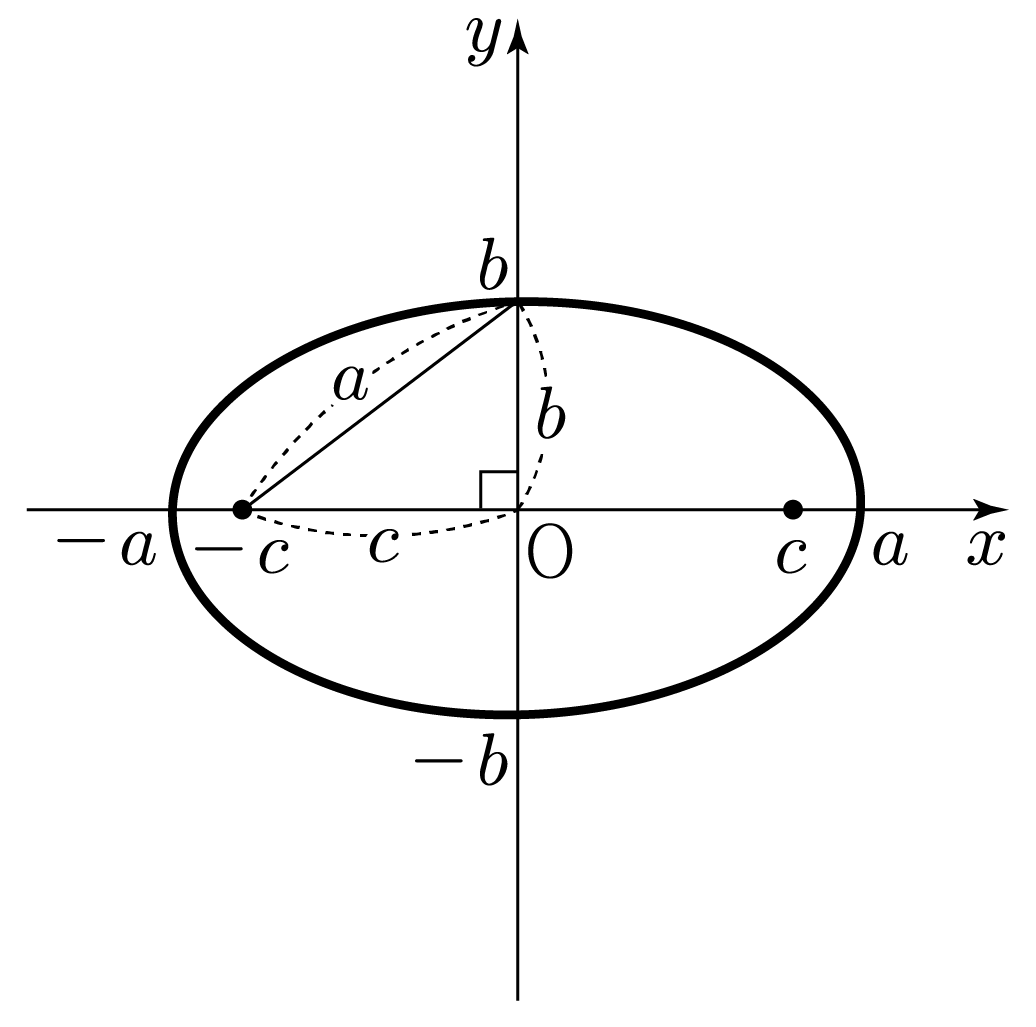
3. 두 초점의 위치를 각각 (−c,0),(c,0)이라 할 때, 피타고라스 정리에 의해 b2+c2=a2이다.
1. y축으로 긴 타원이며, 초점은 y축에 위치한다.
2. 두 초점으로부터 타원의 어느 지점까지의 거리의 합은 2b이다.
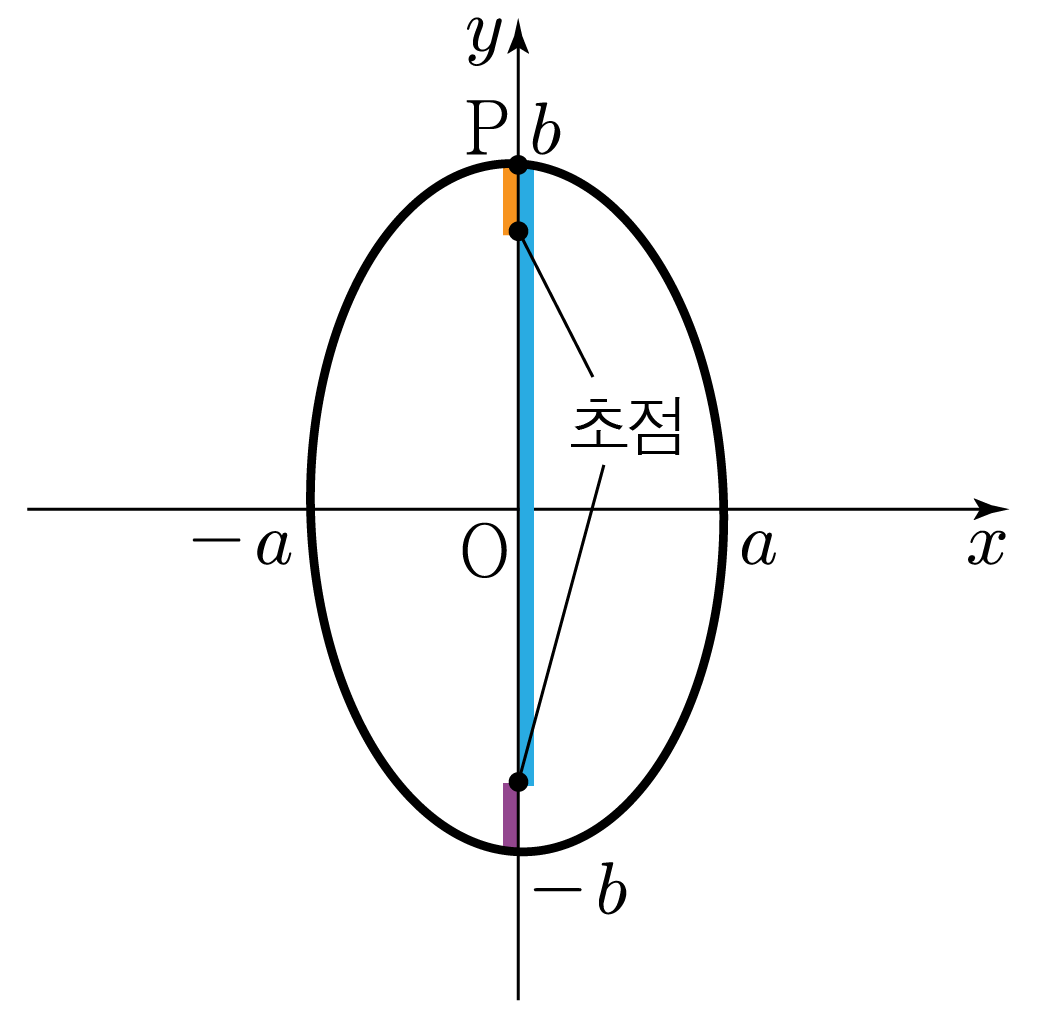
아래 그림과 같이 타원 위의 지점 (0,b)에 점 P가 있다고 해보자.
P와 위쪽에 위치한 초점 사이의 거리는 주황색 선의 길이에 해당하고,
P와 아래쪽에 위치한 초점 사이의 거리는 파란색 선의 길이에 해당한다.
이때, 주황색 선의 길이는 보라색 선의 길이와 같다.
그러므로 두 초점으로부터 타원의 어느 지점까지의 거리의 합은 보라색 선의 길이와 파란색 선의 길이의 합인 2b임을 알 수 있다.
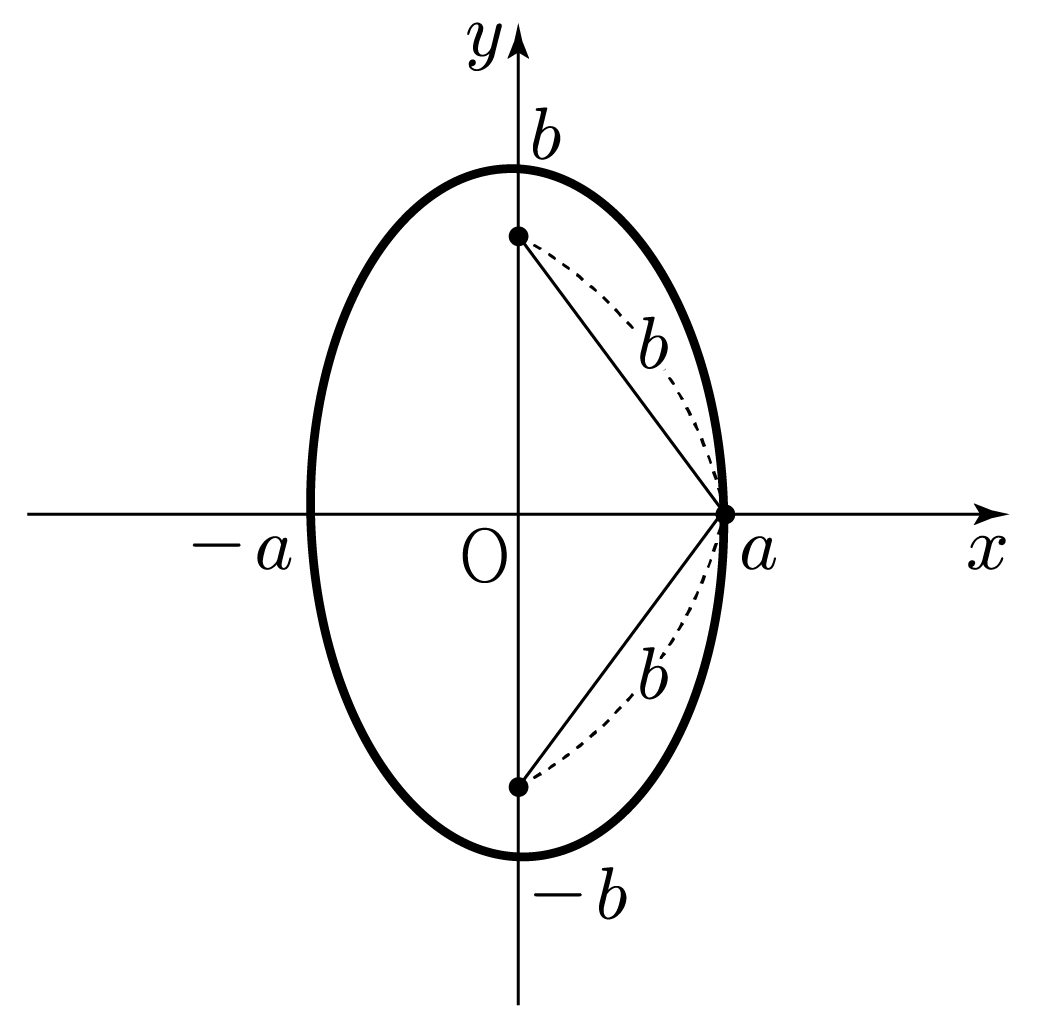
두 초점으로부터 타원의 어느 지점까지의 거리의 합이 2b이므로
아래 그림과 같이 타원 위의 지점 (a,0)과 각 초점 사이의 거리는 b로 같다.
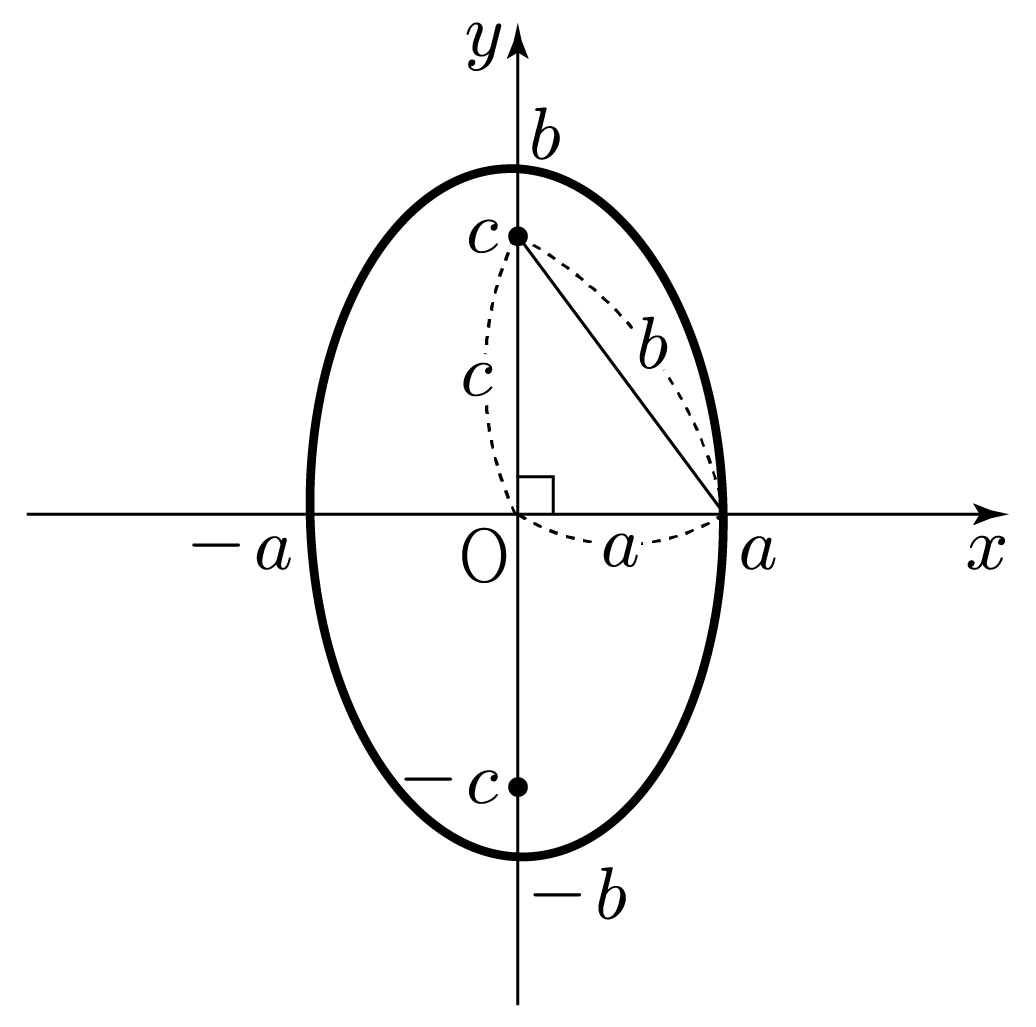
3. 두 초점의 위치를 각각 (0,−c),(0,c)라 할 때, 피타고라스 정리에 의해 a2+c2=b2이다.
장반경은 타원의 가장 긴 반지름, 단반경은 타원의 가장 짧은 반지름이다.
a2x2+b2y2=1에서 a와 b 중 큰 값이 장반경, 작은 값이 단반경이다.
타원 4x2+9y2=1의 장반경과 단반경을 구해보자.
4x2+9y2=22x2+32y2=1이므로
a2x2+b2y2=1에서 a=2,b=3에 해당한다.
a와 b 중 큰 값이 장반경, 작은 값이 단반경이므로 장반경은 3, 단반경은 2이다.
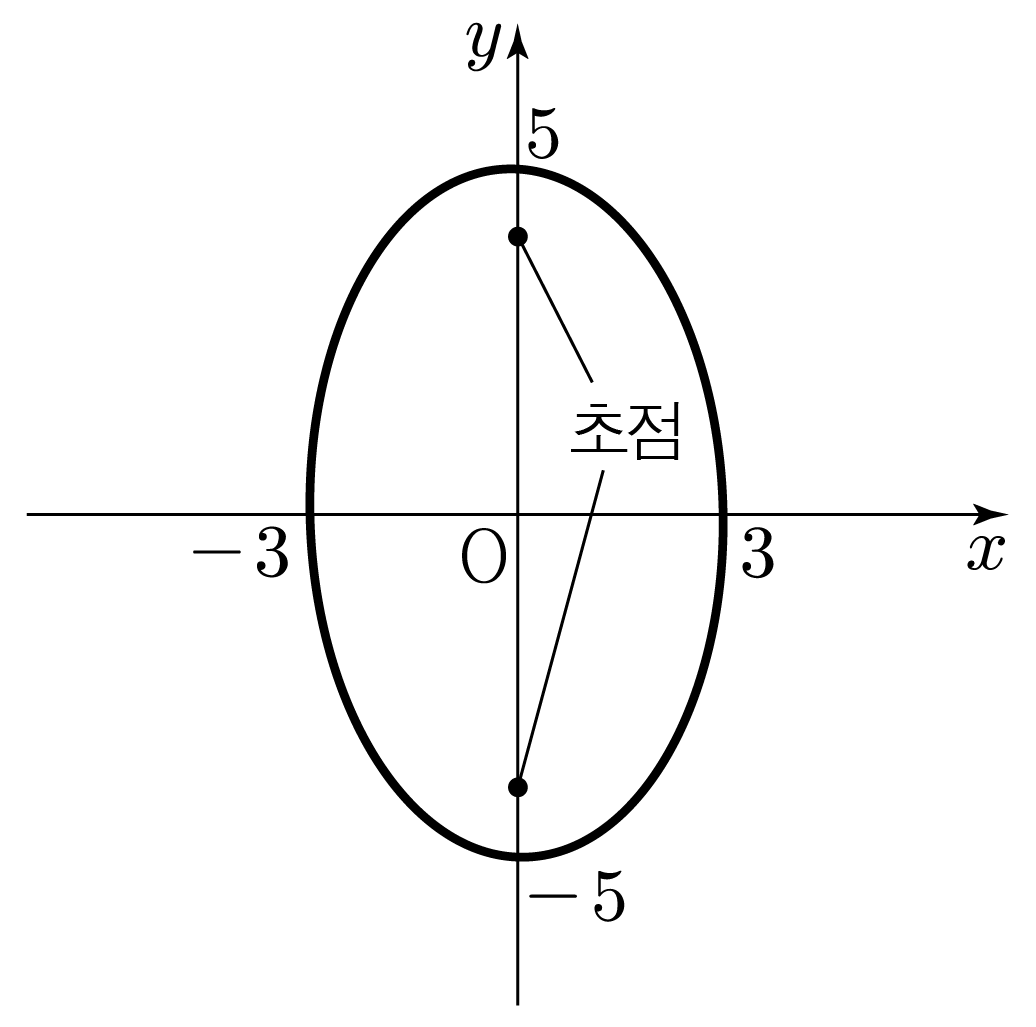
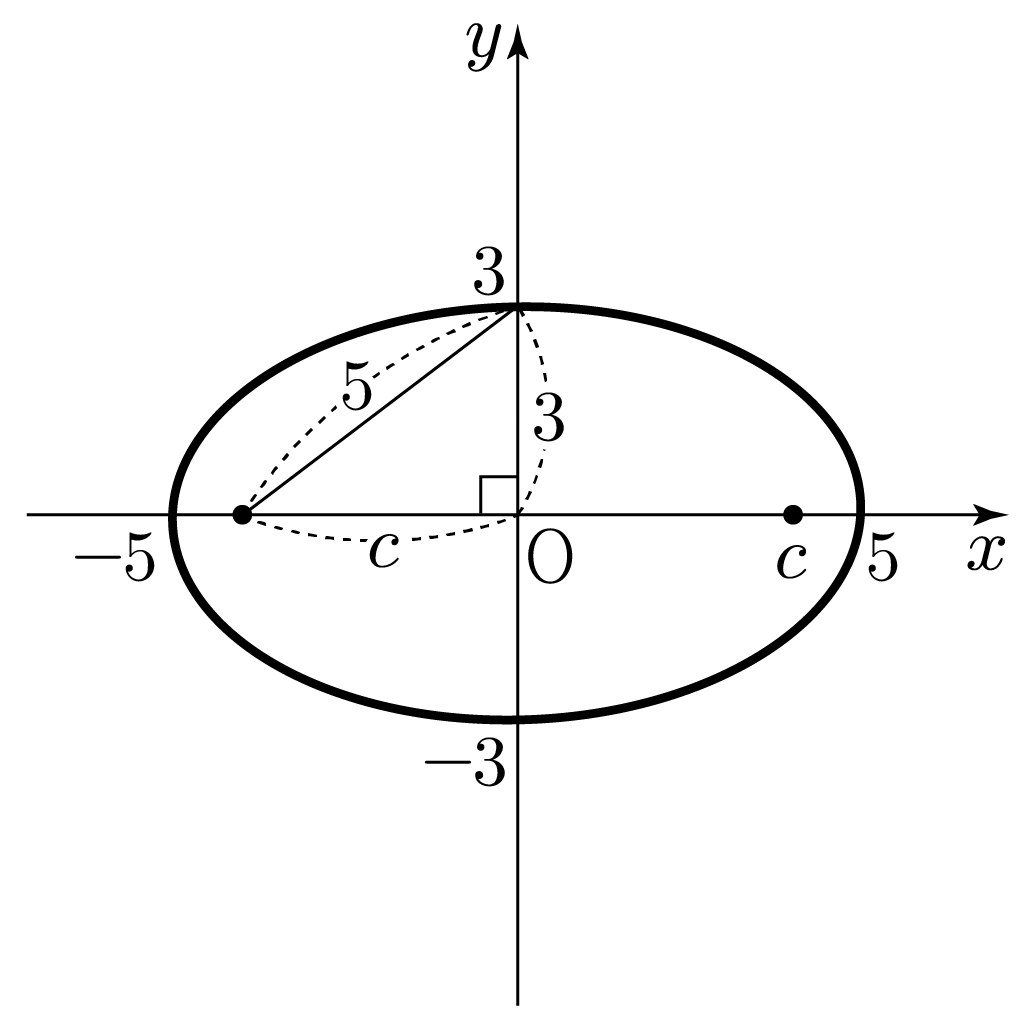
타원 9x2+25y2=1을 초점과 함께 그려보자.
9x2+25y2=32x2+52y2=1이므로 a2x2+b2y2=1에서
1. a=3,b=5에 해당한다.
b>a이므로 y축으로 긴 타원이며, 초점은 y축에 위치한다.
2. a와 b 중 큰 값이 장반경, 작은 값이 단반경이므로 장반경은 5, 단반경은 3이다.
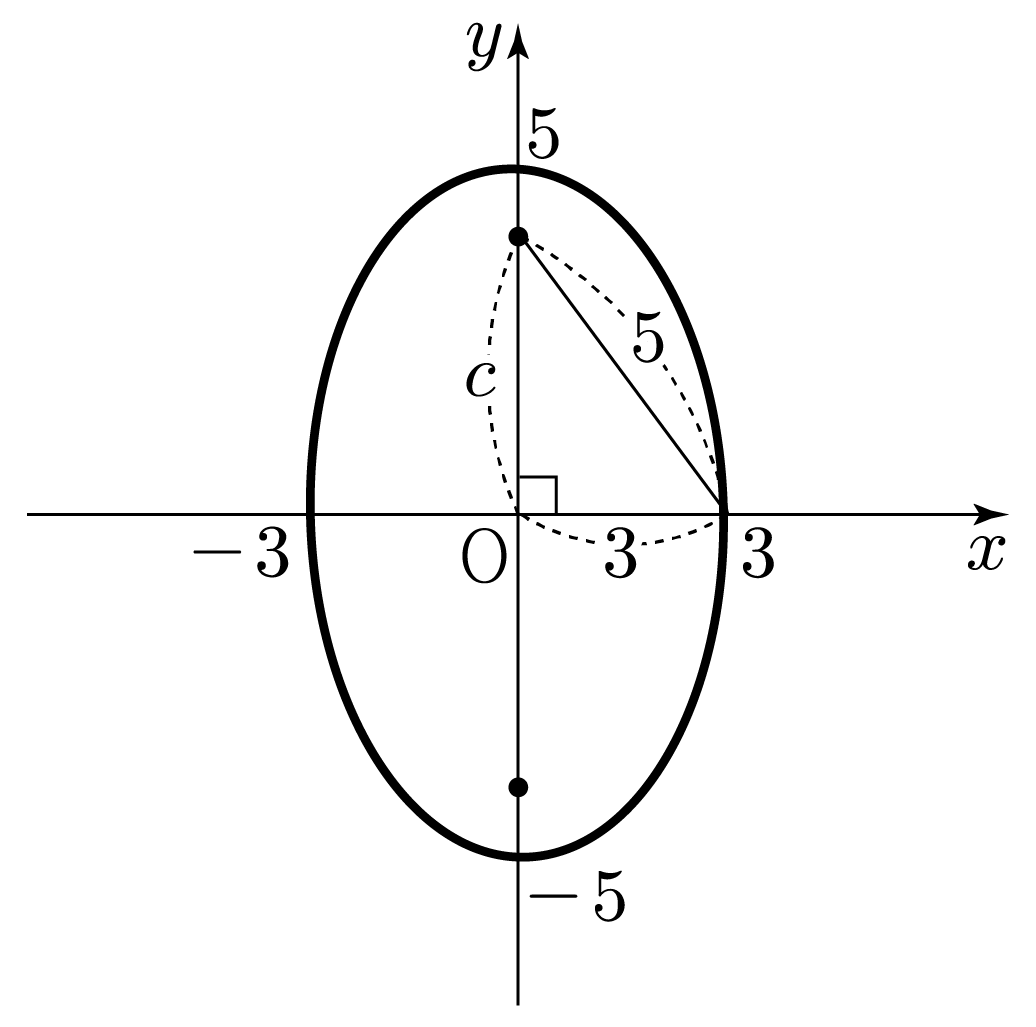
3. 두 초점의 위치를 각각 (0,−c),(0,c)라 할 때, 피타고라스 정리에 의해 32+c2=52이다.
32+c2=52,
9+c2=25,
c2=25−9,
c2=16,
c2=42인데, 이때 c는 양수이므로
c=4이다.
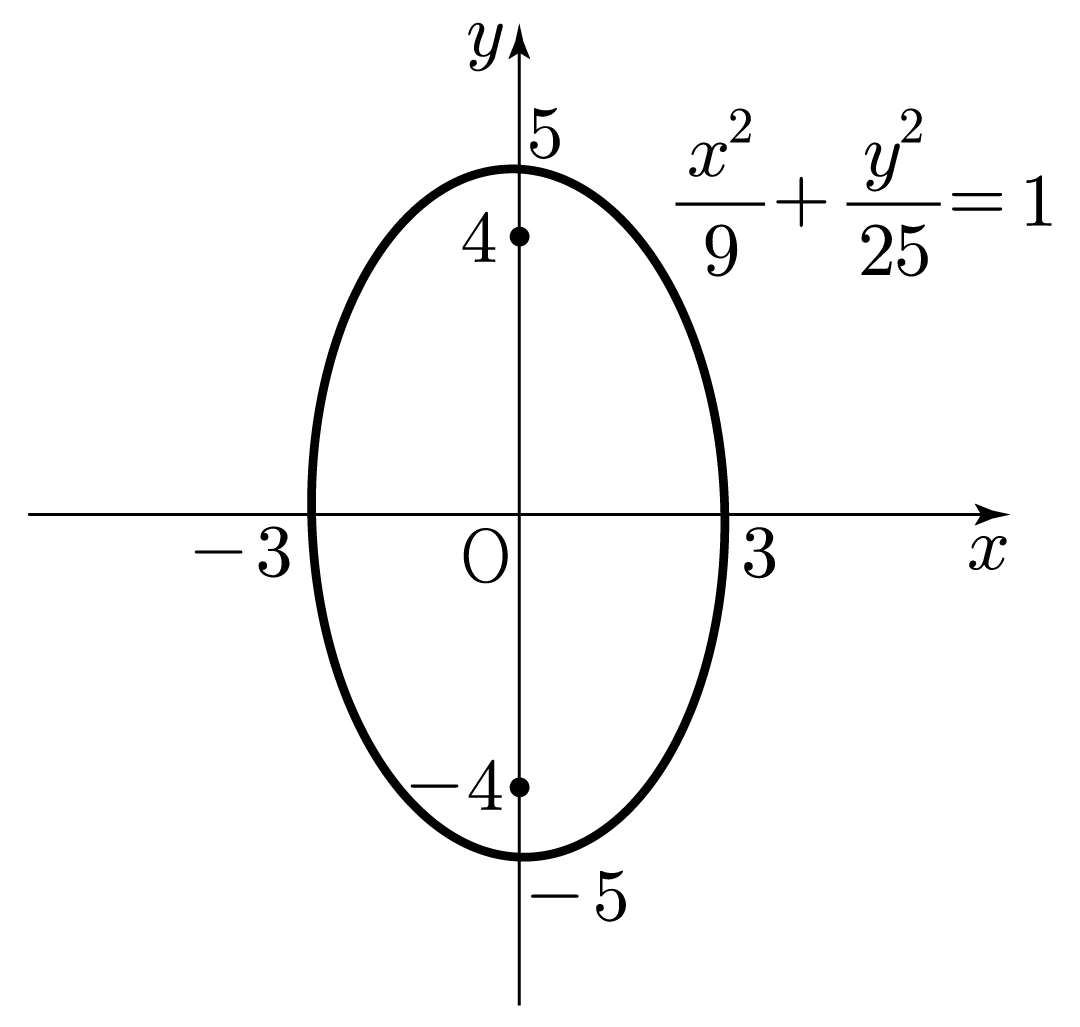
4. 구한 내용을 바탕으로 타원과 초점을 그리면 아래 그림과 같다.
c를 장반경으로 나눈 물리량으로, 원에 비해 얼마나 찌그러졌는지를 나타낸다.
이심률이 0에 가까울수록 타원은 원에 가깝다. 이심률을 기호로 표기할 때, e로 표기한다.
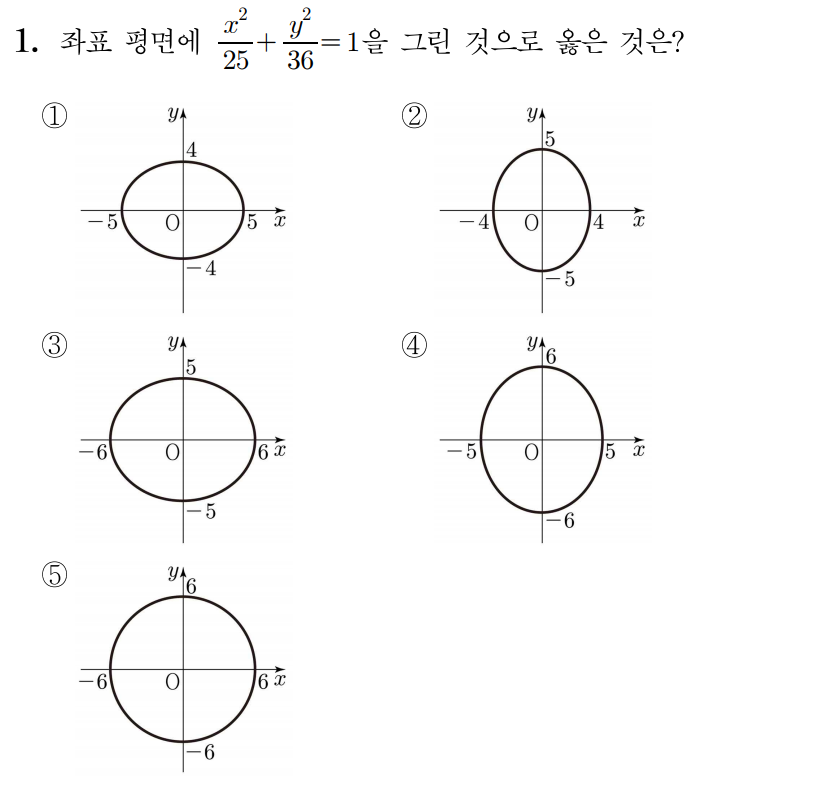
타원 25x2+9y2=1의 이심률을 구해보자.
25x2+9y2=52x2+32y2=1이므로 a2x2+b2y2=1에서
1. a=5,b=3에 해당한다.
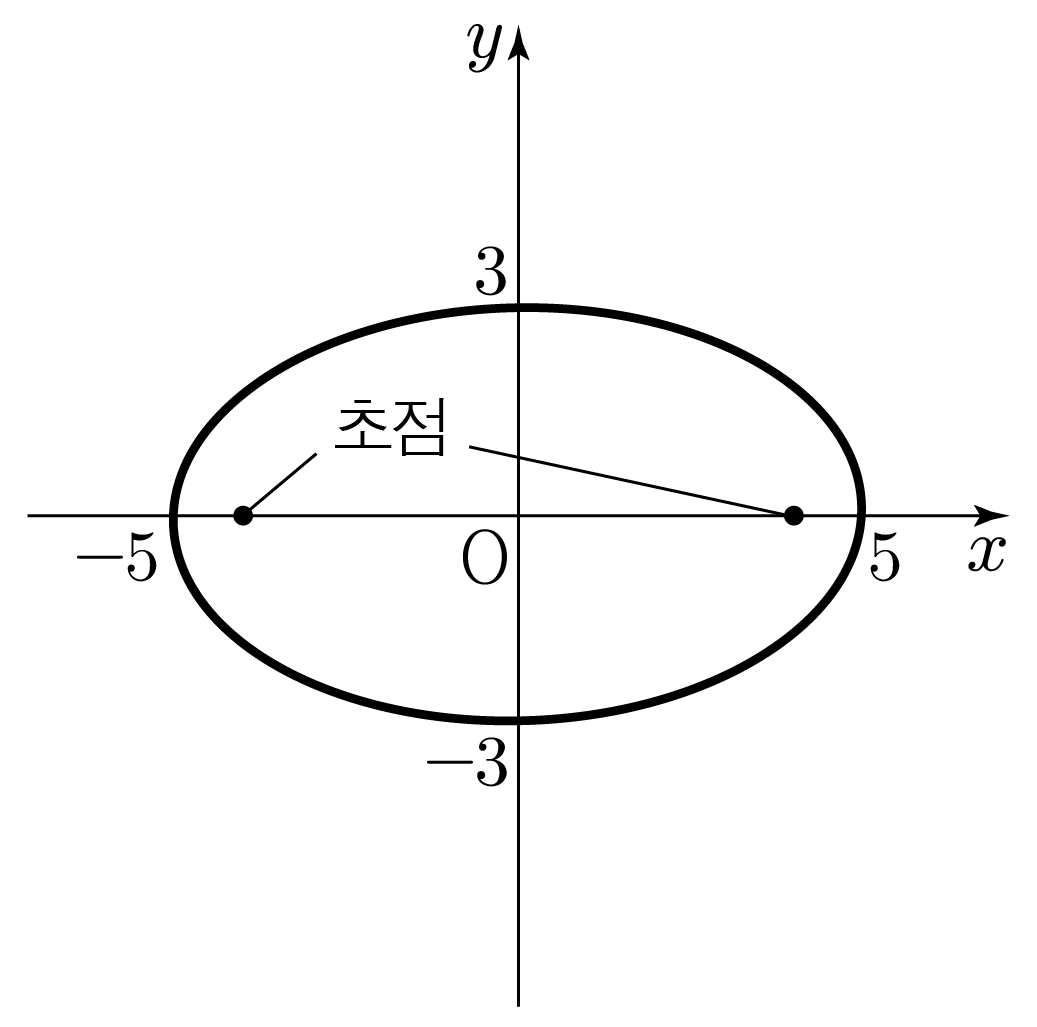
a>b이므로 x축으로 긴 타원이며, 초점은 x축에 위치한다.
2. a와 b 중 큰 값이 장반경, 작은 값이 단반경이므로 장반경은 5, 단반경은 3이다.
3. 두 초점의 위치를 각각 (−c,0),(c,0)이라 할 때, 피타고라스 정리에 의해 32+c2=52이다.
32+c2=52,
9+c2=25,
c2=25−9,
c2=16,
c2=42인데, 이때 c는 양수이므로
c=4이다.
4. 이심률 e는 c를 장반경으로 나눈 물리량이다.
c=4, 장반경은 5이므로 e=4÷5=54이다.
정답: $4$
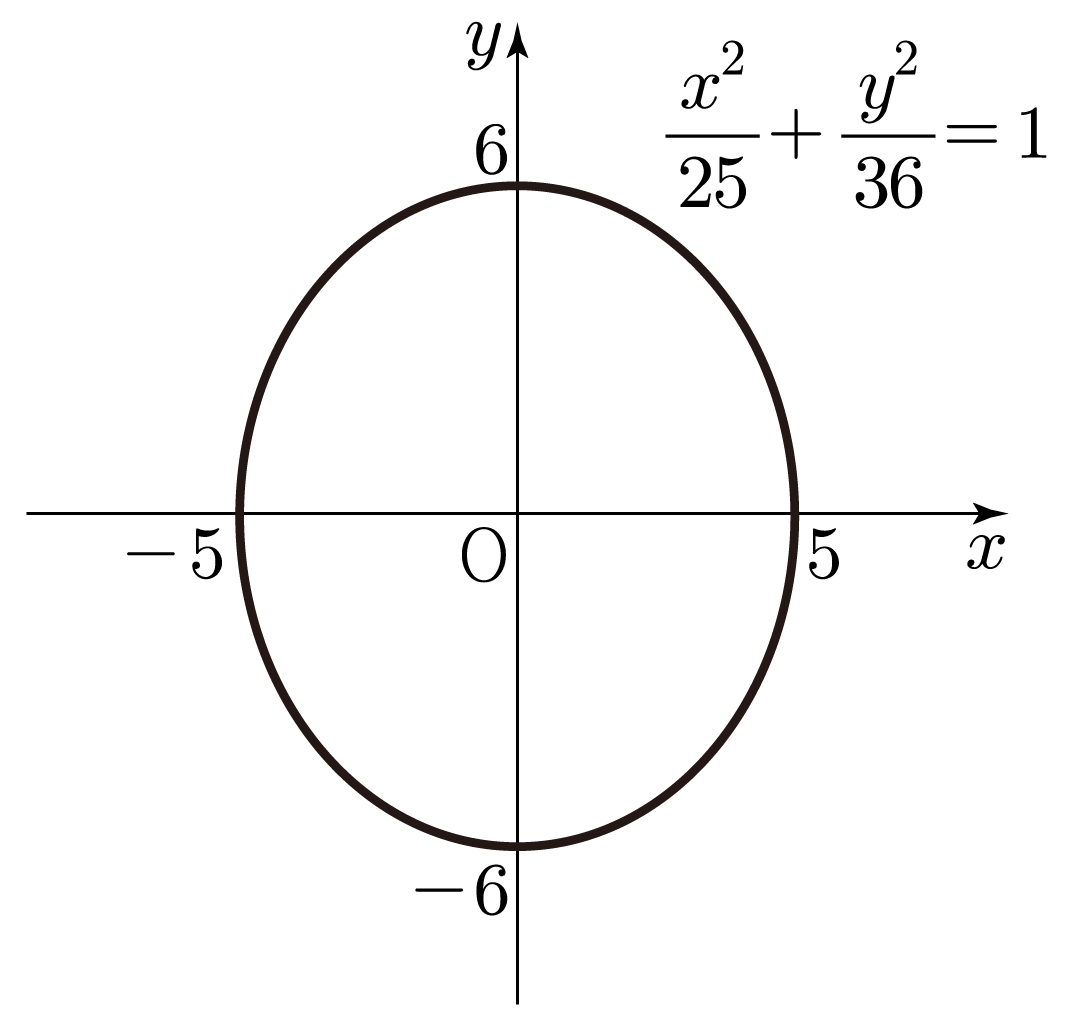
25x2+36y2=52x2+62y2=1이므로 a2x2+b2y2=1에서
a=5, b=6에 해당한다.
b>a이므로 y축으로 긴 타원이며, 초점은 y축에 위치한다.
구한 내용을 바탕으로 타원을 그리면 아래 그림과 같다.
따라서 정답은 4번이다.

정답: $4$
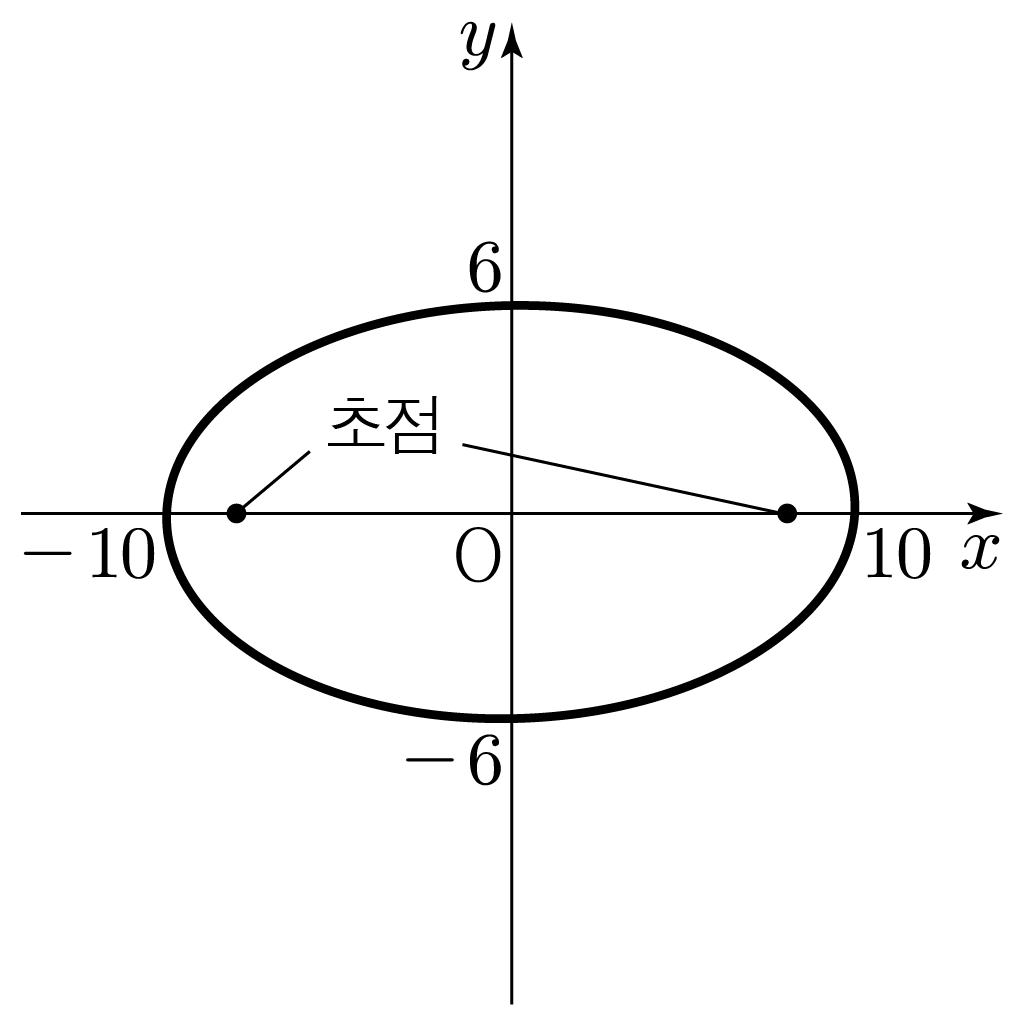
100x2+36y2=102x2+62y2=1이므로 a2x2+b2y2=1에서
1. a=10,b=6에 해당한다.
a>b이므로 x축으로 긴 타원이며, 초점은 x축에 위치한다.
2. a와 b 중 큰 값이 장반경, 작은 값이 단반경이므로 장반경은 10, 단반경은 6이다.
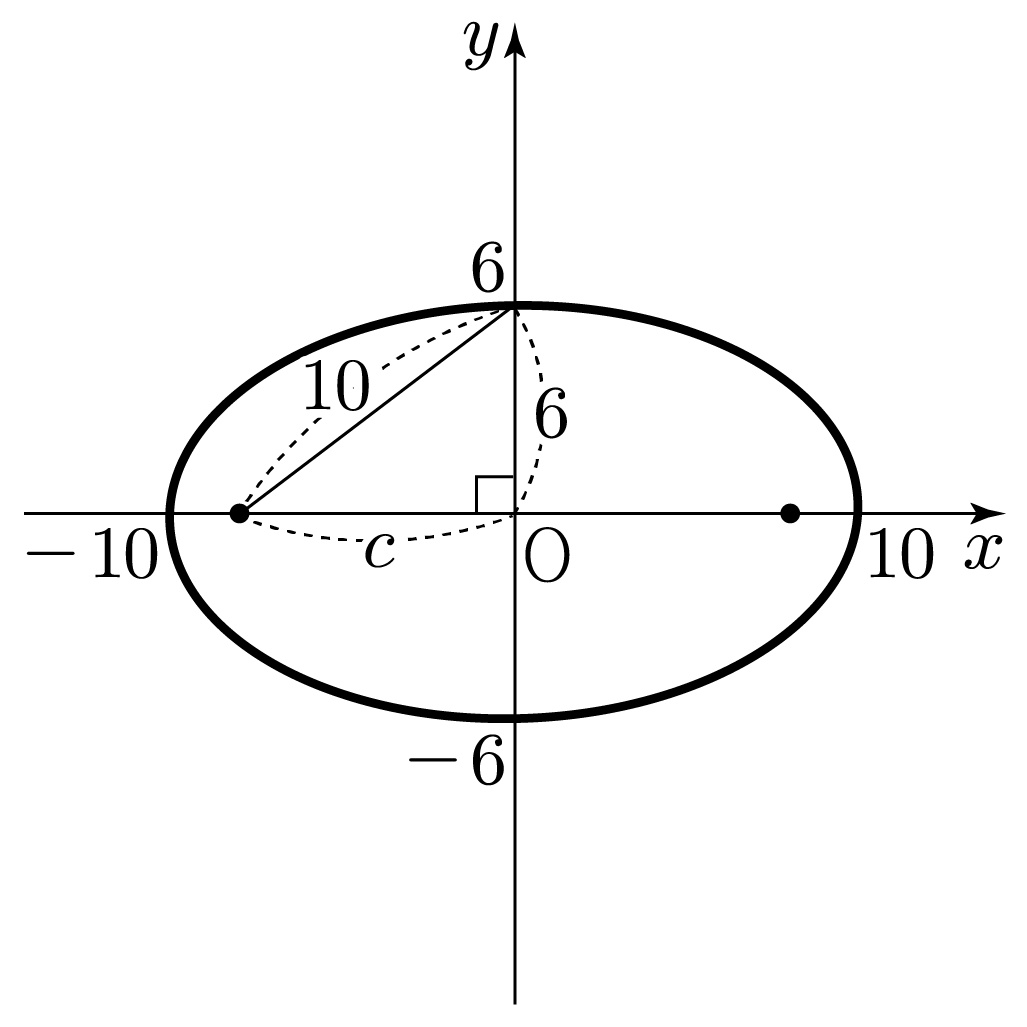
3. 두 초점의 위치를 각각 (−c,0),(c,0)이라 할 때, 피타고라스 정리에 의해 62+c2=102이다.
62+c2=102,
36+c2=100,
c2=100−36,
c2=64,
c2=82인데, 이때 c는 양수이므로
c=8이다.
4. 이심률 e는 c를 장반경으로 나눈 물리량이다.
c=8, 장반경은 10이므로 e=8÷10=108=54이다.
따라서 정답은 4번이다.