¶ 지식 정보
| 해당 지식 | |
|---|---|
|
|
| 하위 지식 | 상위 지식 |
|
|
¶ 그래프
함수의 입력값과 출력값을 좌표 평면에 그려 나타낸 것이다. 좌표(좌표 평면)에 나타낼 경우 입력값을 , 출력값을 로 한다.
¶ 절편
그래프가 축과 만나는 지점이다.
절편은 축과 만나는 지점, 절편은 축과 만나는 지점이다.
¶ 절편 예시
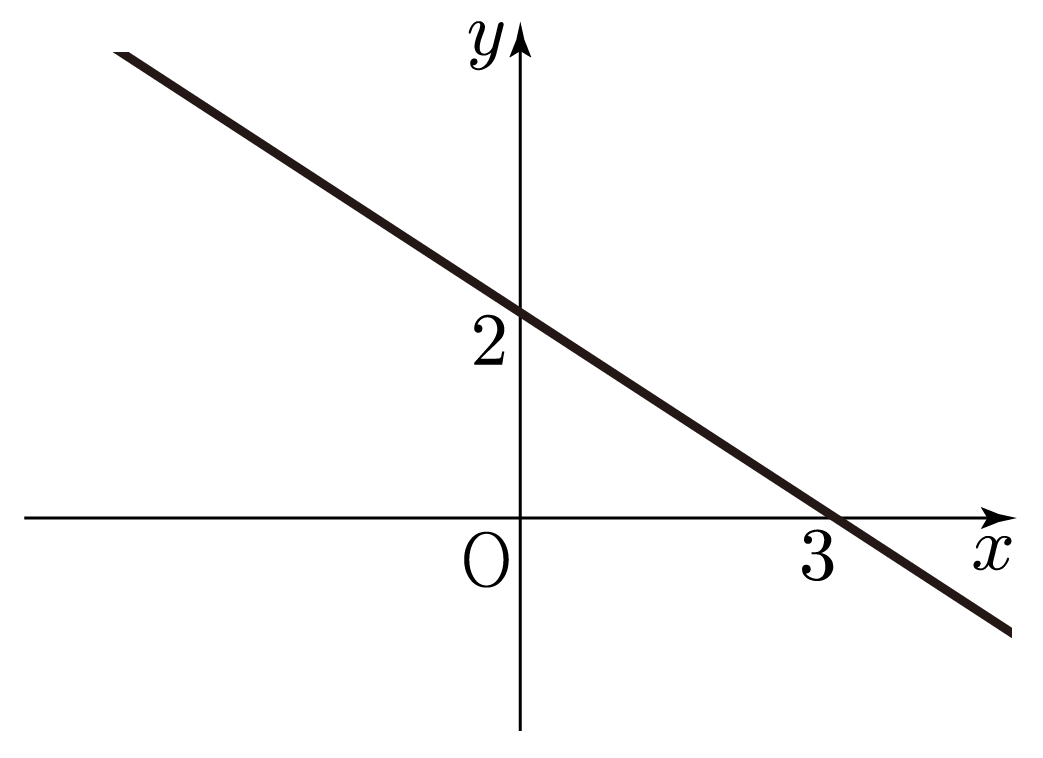
아래 그림과 같은 그래프가 있을 때, 절편은 , 절편은 이다.
¶ 일차함수의 그래프
직선 형태이다.
(는 양수 또는 음수)인 일차함수 식에서 는 기울기이며, 기울기는 가 만큼 증가할 때 의 변화를 나타낸다.
¶ 일차함수의 그래프 예시
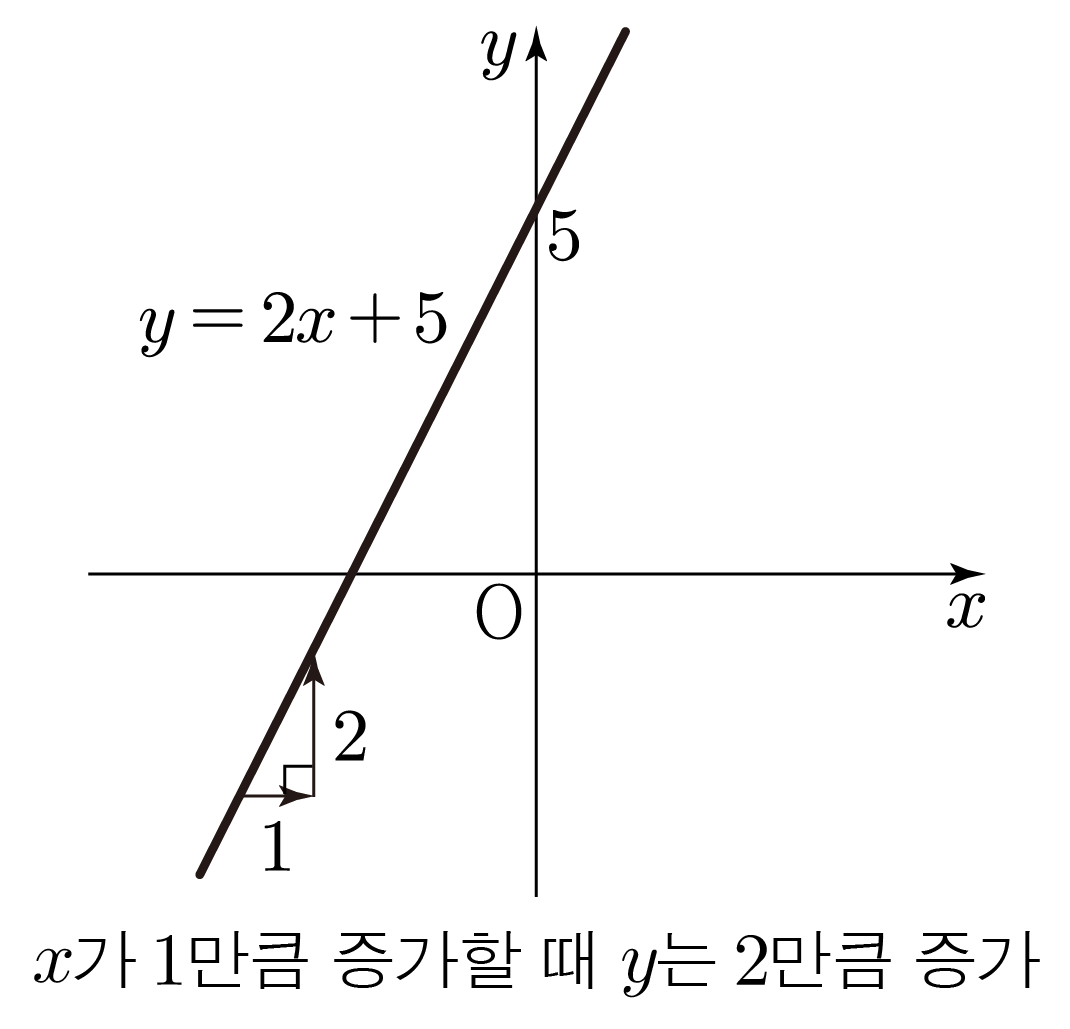
는 에서 이므로 기울기는 이다.
따라서 가 만큼 증가할 때 는 만큼 증가한다.
¶ 일차함수의 그래프 그리기
일차함수의 절편을 구한 후, 기울기를 통해 직선을 그린다.
¶ 일차함수의 그래프 그리기 예시
을 그려보자.
은 에서 이므로 기울기는 이다.
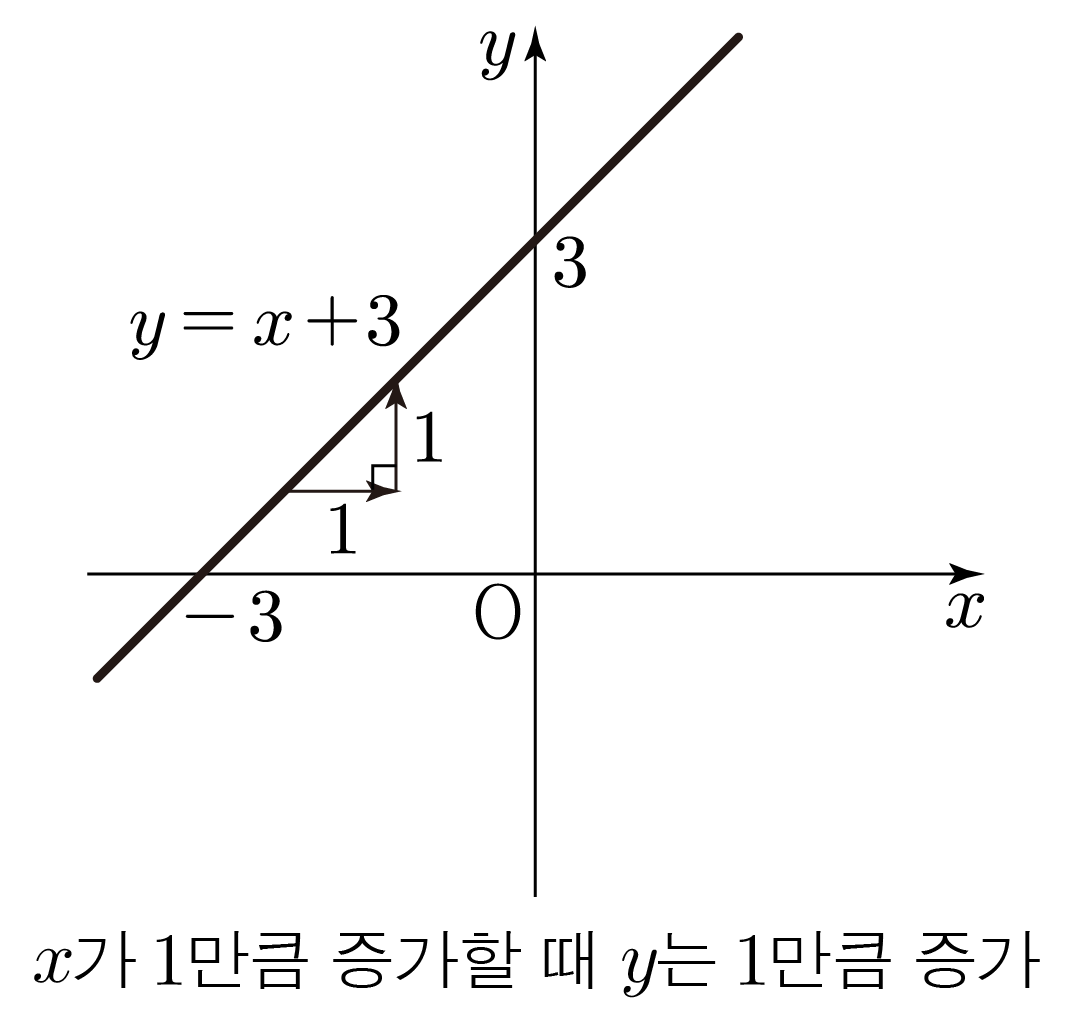
일 때 이므로 절편은 이고, 기울기가 이므로 가 만큼 증가할 때 도 만큼 증가한다.
따라서 을 그리면 아래와 같다.
¶ 이차함수의 그래프
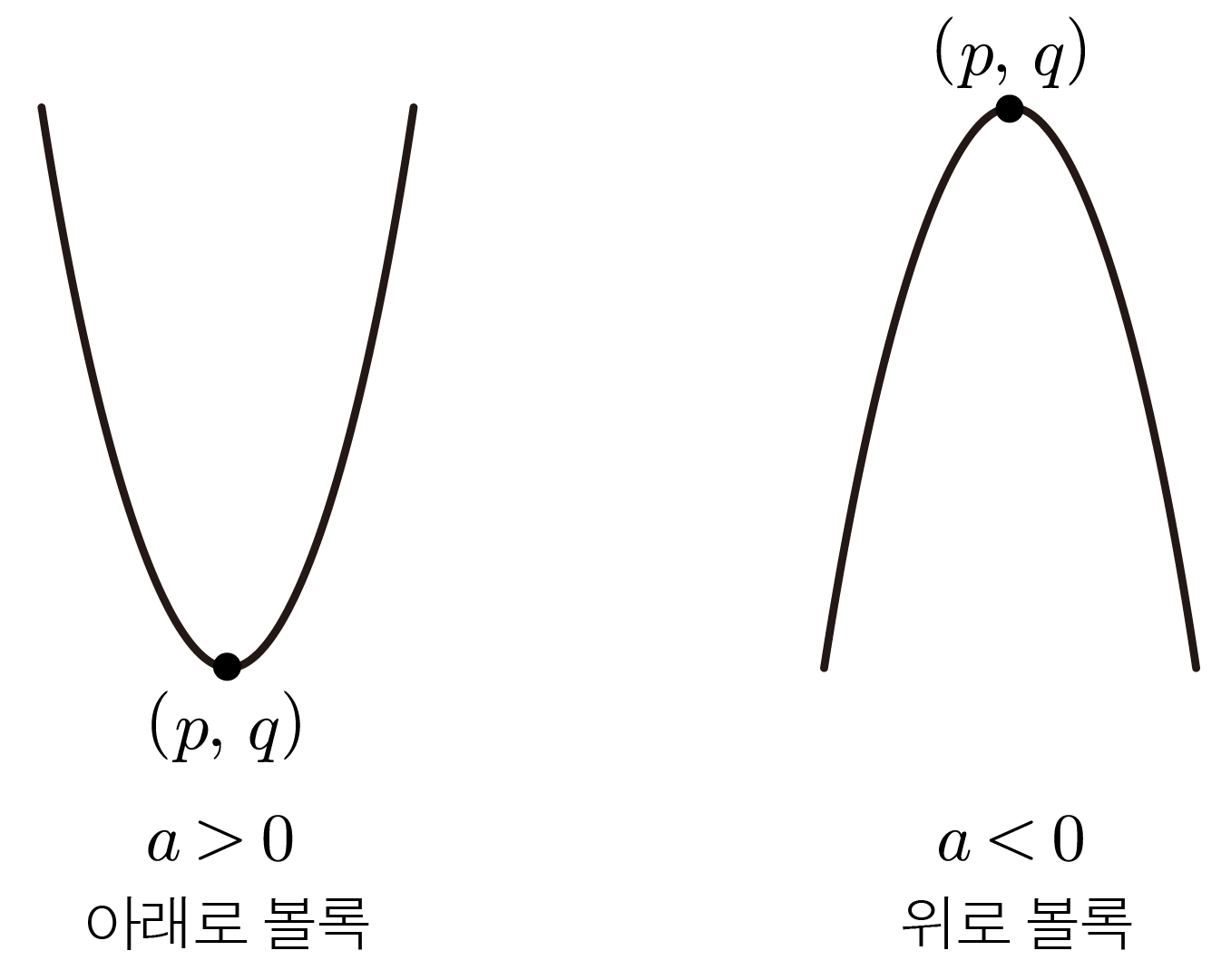
나 와 같이 한쪽이 볼록한 형태이다.
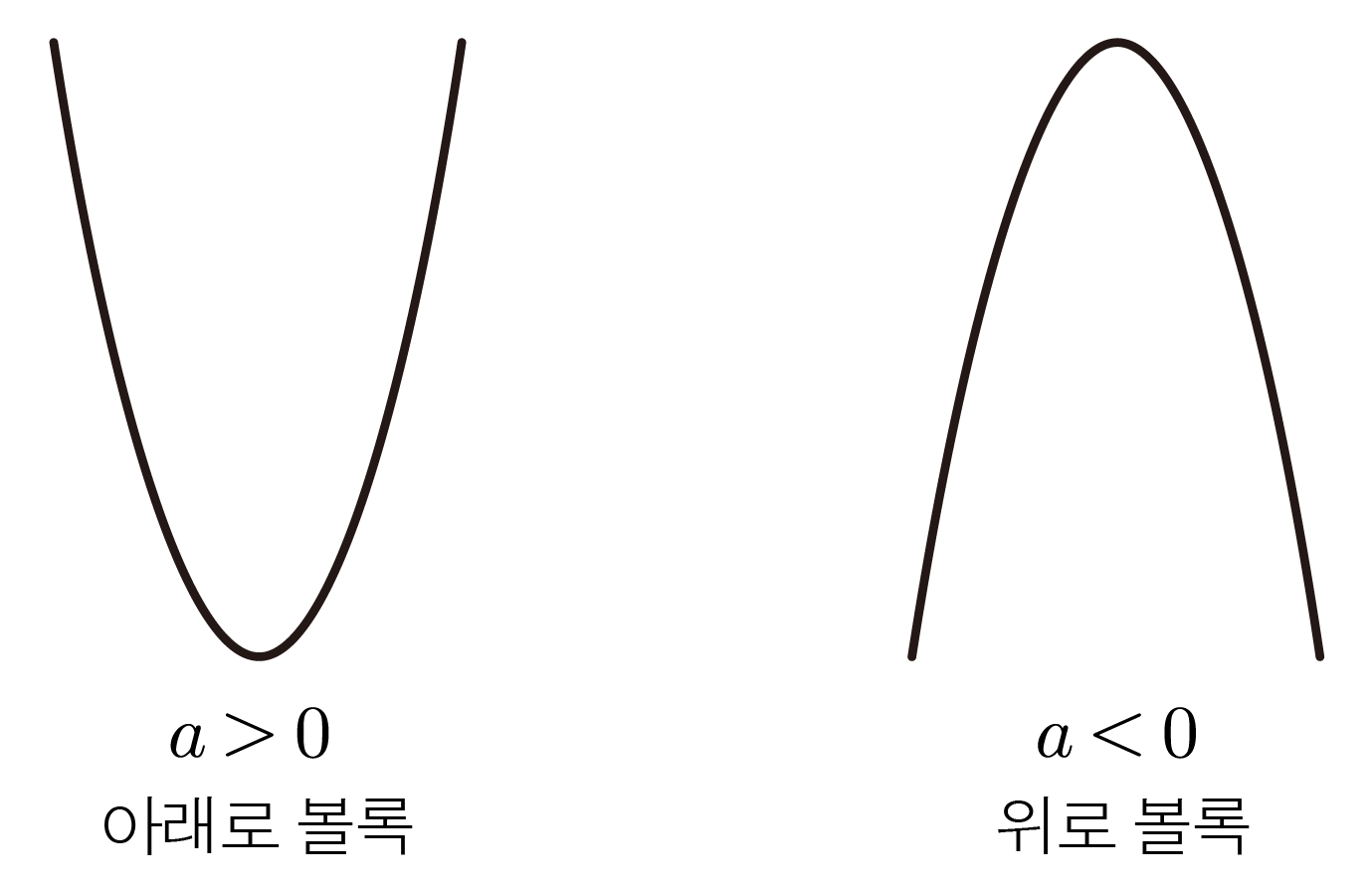
(는 양수 또는 음수)인 이차함수 식에서 인 경우 와 같이 아래로 볼록,
인 경우 와 같이 위로 볼록한 그래프 개형(대략적인 모양)을 갖는다.
¶ 이차함수의 꼭짓점
가장 꼭대기나 바닥에 있는 한 점이다.
인 이차함수 식에서 꼭짓점의 좌표는 이다.
¶ 이차함수의 꼭짓점 예시
인 이차함수 식에서 꼭짓점의 좌표를 구해보자.
에서 이므로 꼭짓점의 좌표는 이다.
¶ 이차함수가 다항식으로 표현된 경우 꼭짓점 구하기
이차함수가 다항식으로 표현된 경우 의 형태로 만들어 꼭짓점을 구한다.
예를 들어 은
이므로 꼭짓점의 좌표는 이다.
¶ 이차함수의 그래프 그리기
인 이차함수 식에서
-
인 경우:
꼭짓점이 가장 아래쪽에 위치하도록 아래로 볼록한 그래프를 그린다. -
인 경우:
꼭짓점이 가장 위쪽에 위치하도록 위로 볼록한 그래프를 그린다.
¶ 이차함수의 그래프 그리기 예시
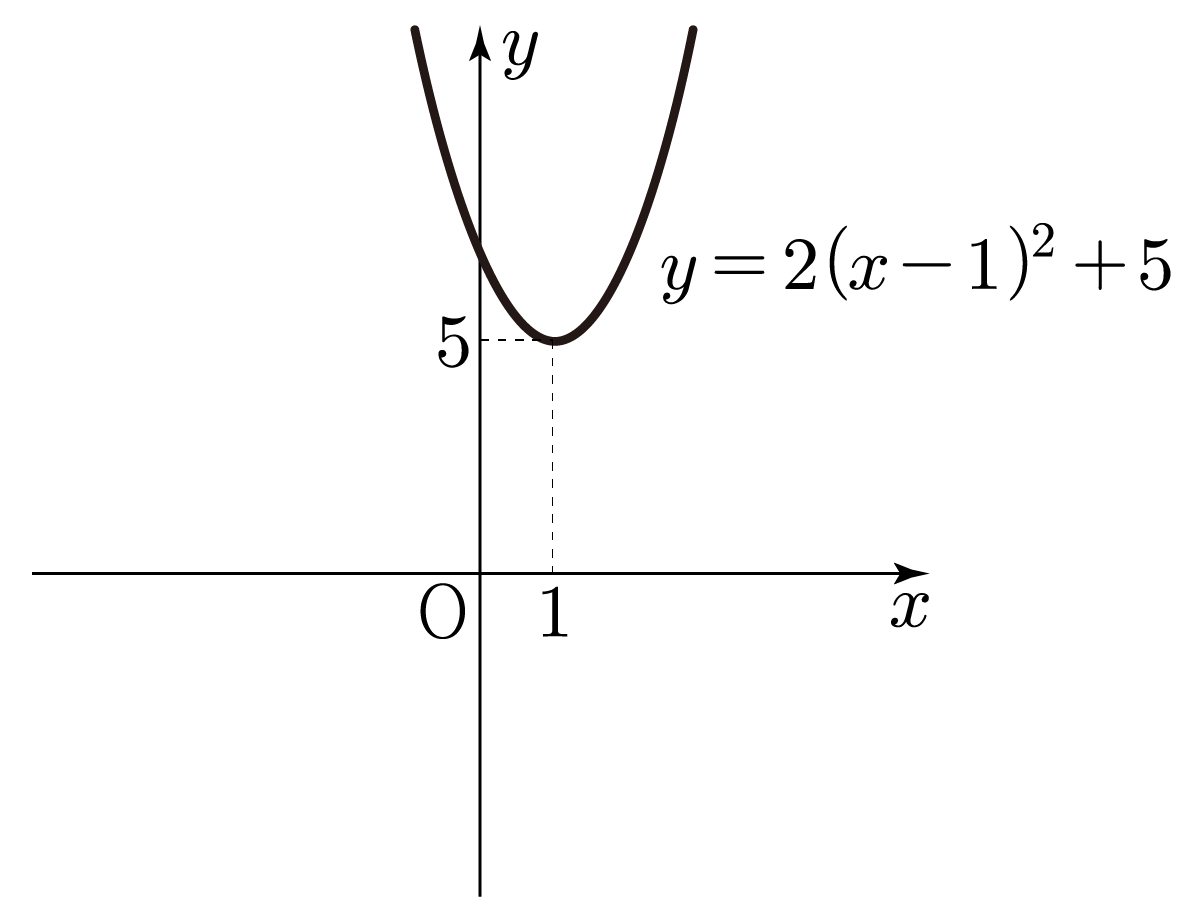
를 그려보자.
에서 이다.
이므로 그래프는 아래로 볼록하며, 이므로 꼭짓점의 좌표는 이다.
따라서 꼭짓점이 가장 아래쪽에 위치하도록 아래로 볼록한 그래프를 그리면 아래와 같다.
¶ 적용 문항
¶ 1번 문항
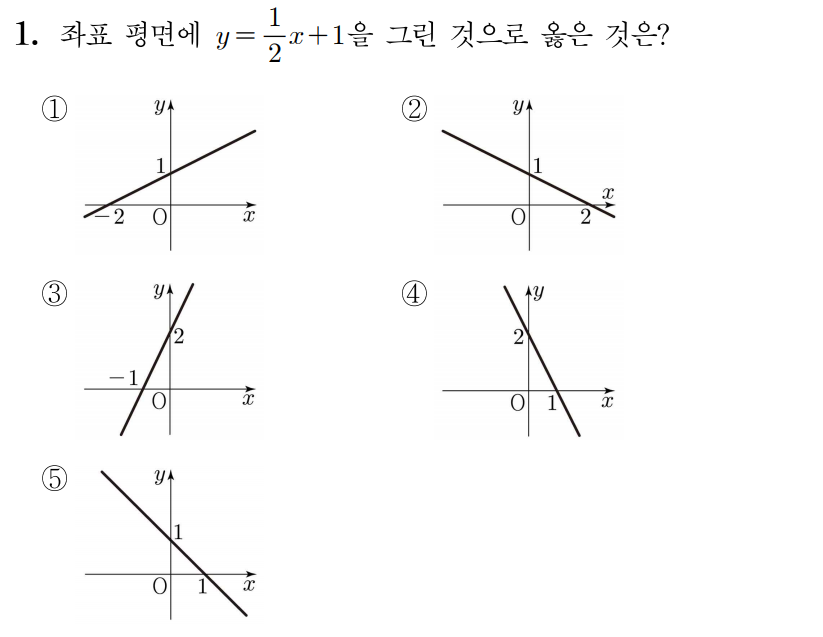
정답: $1$
은 에서 이므로 기울기는 이다.
일 때 이므로 절편은 이고, 기울기가 이므로 가 만큼 증가할 때 는 만큼 증가한다.
그러므로 을 그리면 아래와 같다.
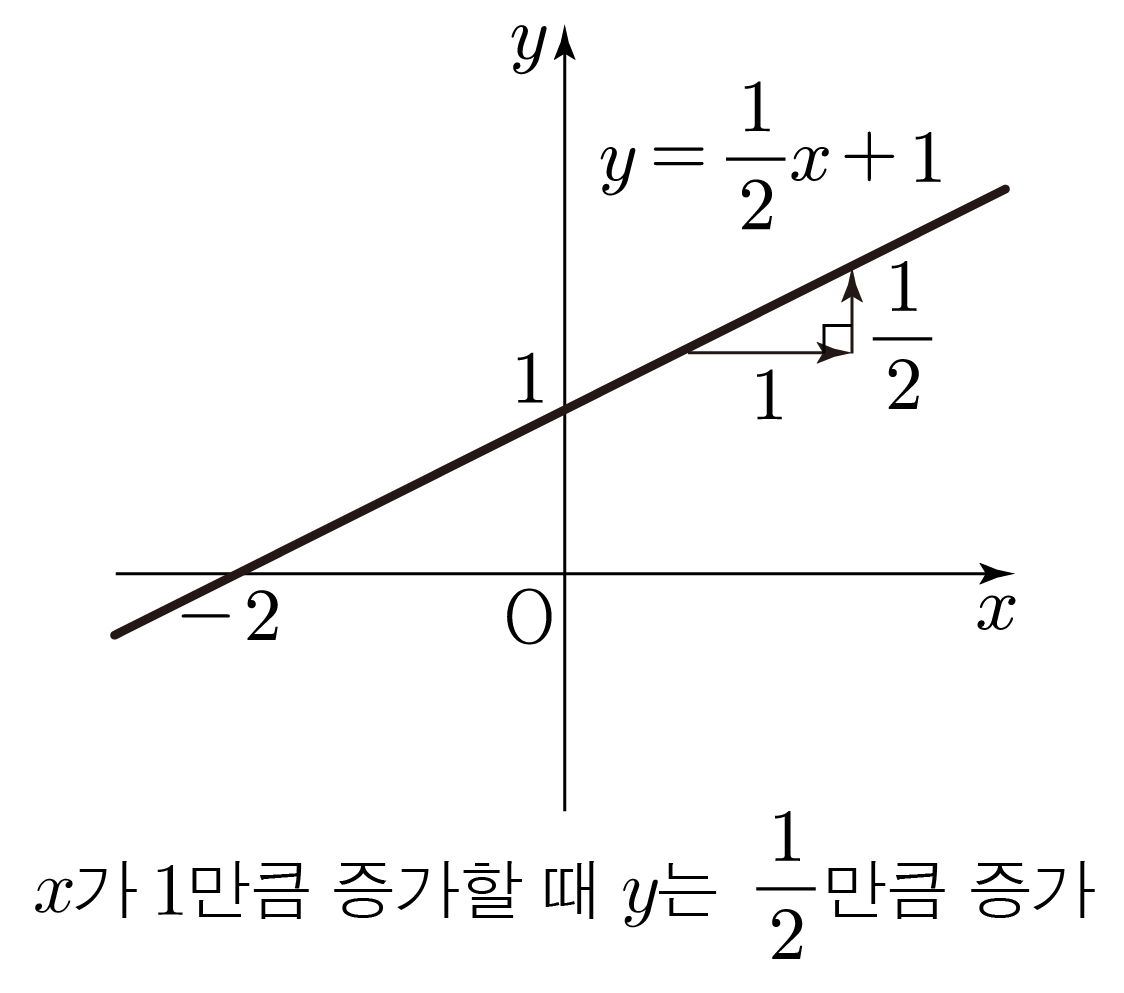
따라서 정답은 번이다.
¶ 2번 문항
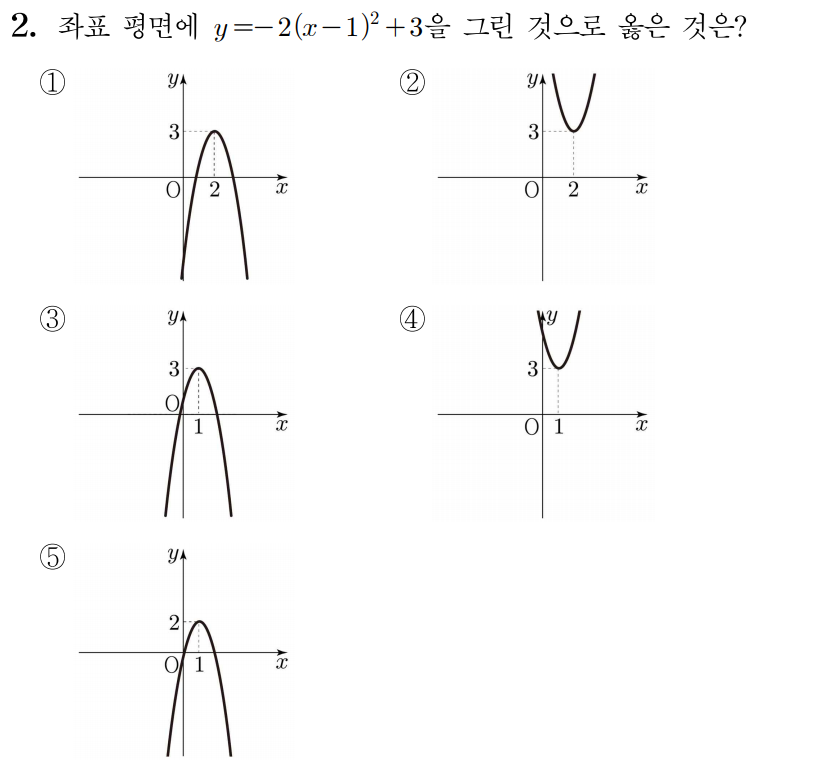
정답: $3$
을 그려보자.
에서 이다.
이므로 그래프는 위로 볼록하며, 이므로 꼭짓점의 좌표는 이다.
그러므로 꼭짓점이 가장 위쪽에 위치하도록 위로 볼록한 그래프를 그리면 아래와 같다.
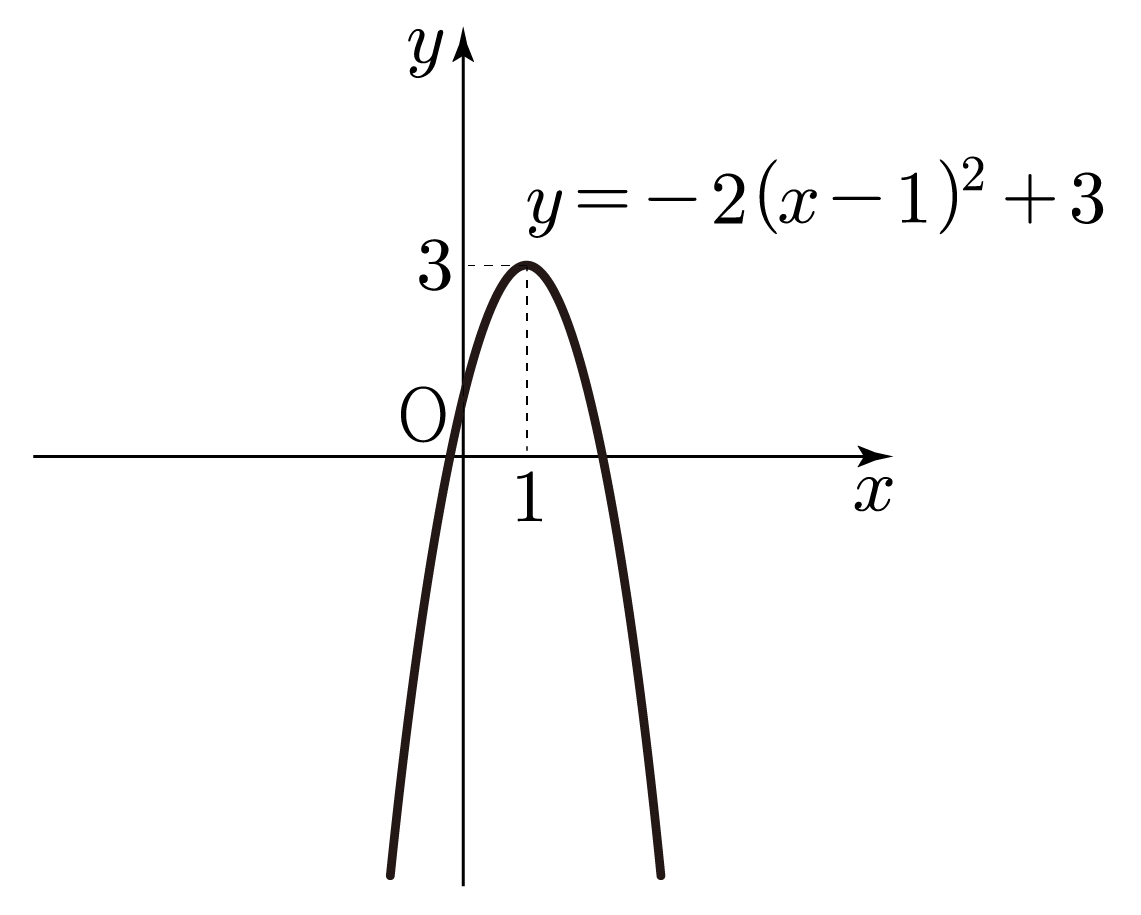
따라서 정답은 번이다.