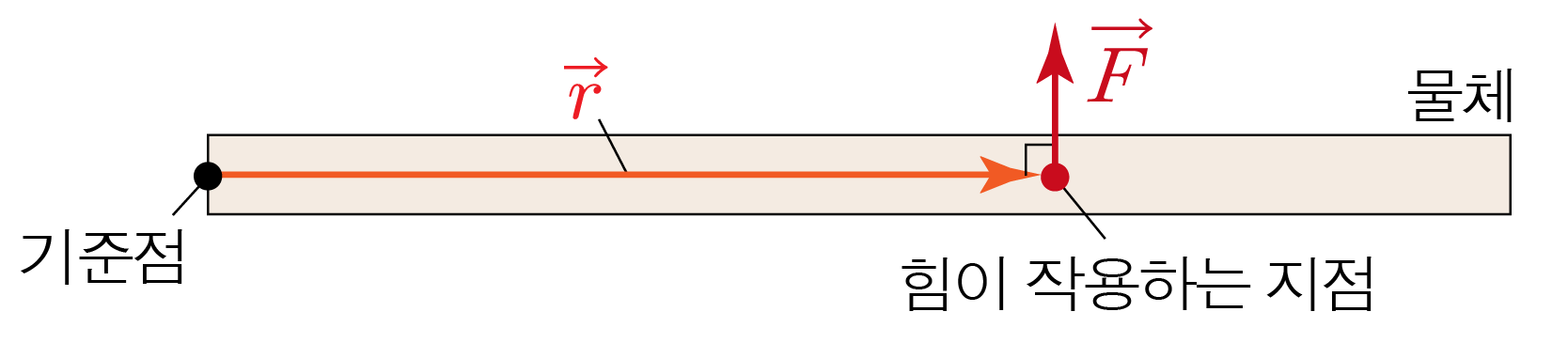
기준점으로부터 힘이 작용한 지점까지의 벡터를 r → r r → r F → F r → × F → r × F N ⋅ m N ⋅ m τ τ
아래 그림과 같이 물체에 r → r F → F r → × F → r × F ( + ) ( + ) ( − ) ( − )
물체가 정지해 있거나 등속도 운동을 하는 상태이다.
평형 상태인 물체는 아래의 조건을 모두 만족한다.
물체에 작용하는 알짜힘이 0 0
기준점으로부터 물체에 작용하는 돌림힘의 합이 0 0
기준점은 어느 곳을 잡아도 상관없다.
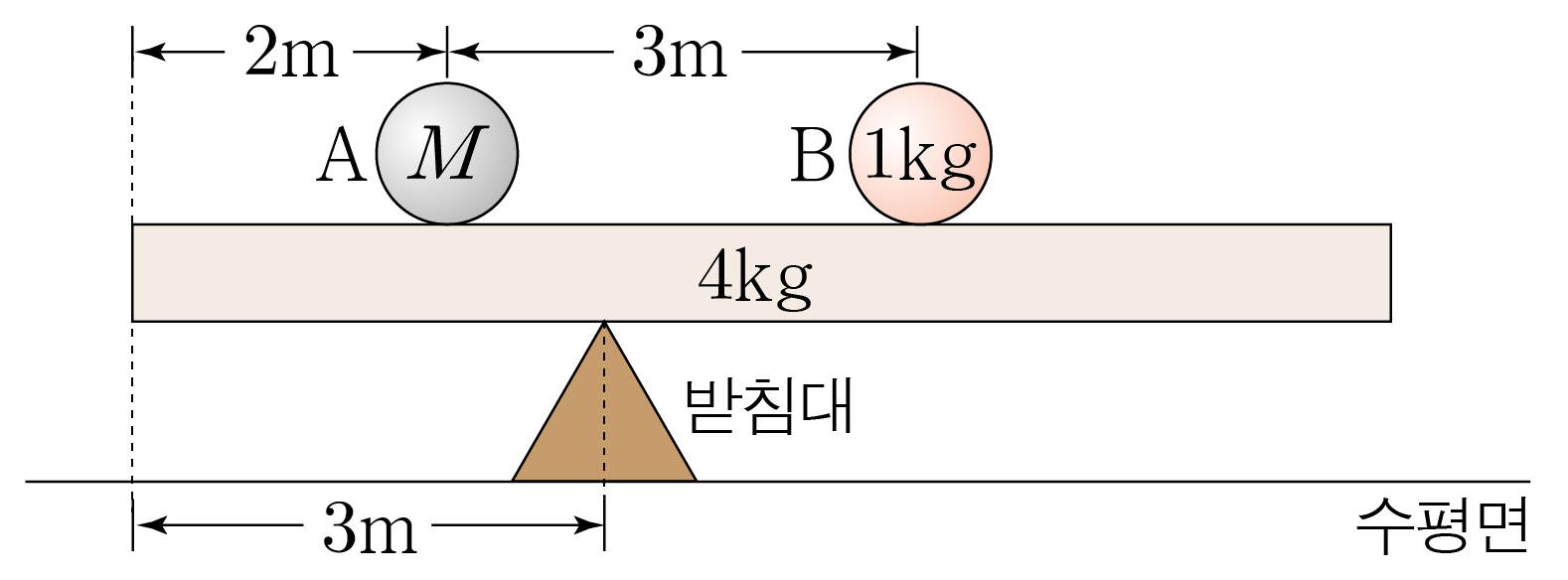
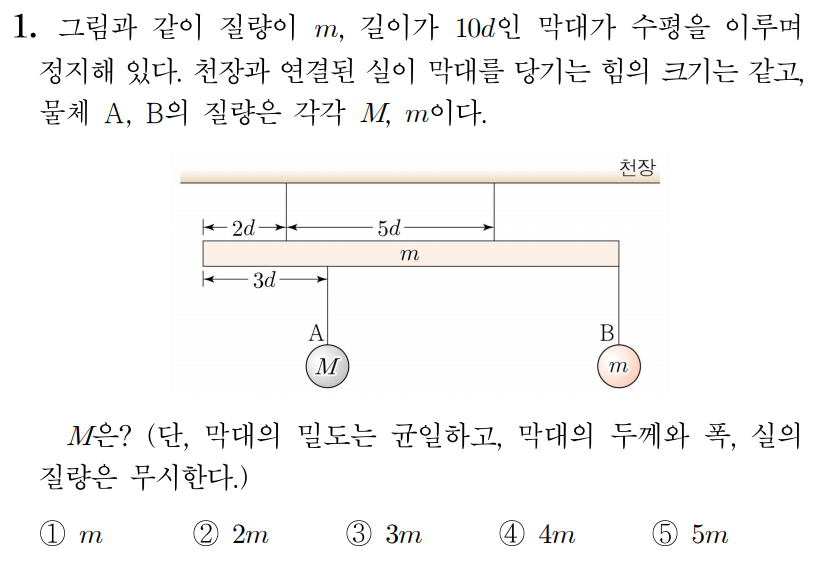
그림과 같이 받침대에 놓인 막대가 수평으로 평형을 유지하고 있고, 막대 위에 물체 A A B B A A B B 4 k g 4 k g M M 1 k g 1 k g 8 m 8 m M M 10 m / s 2 1 0 m / s 2
∘ ∘
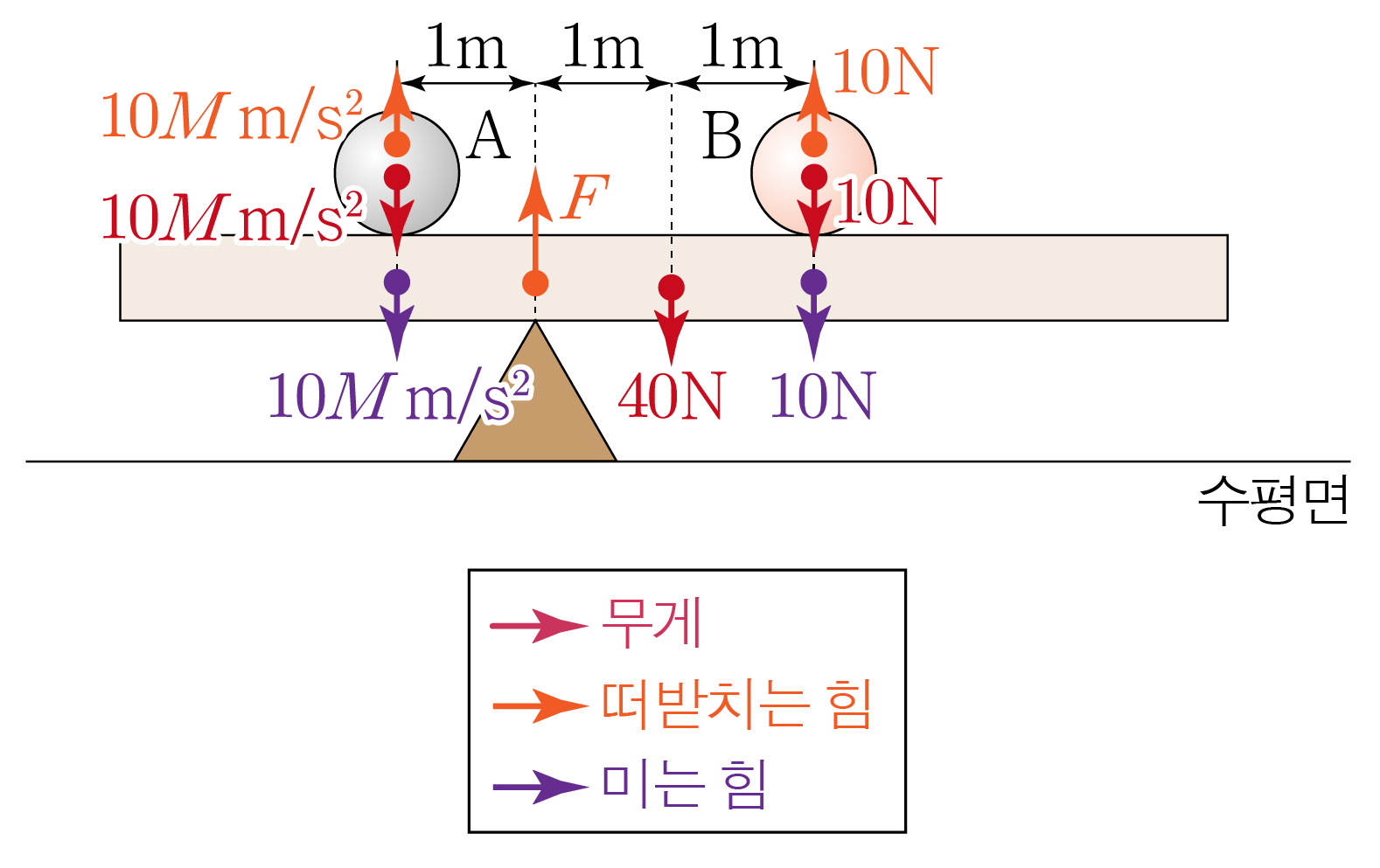
물체가 막대를 누르는 힘과 막대의 무게를 구하면 아래와 같다.
A A M × 10 m / s 2 = 10 M M × 1 0 m / s 2 = 1 0 M B B 1 k g × 10 m / s 2 = 10 k g ⋅ m / s 2 = 10 1 k g × 1 0 m / s 2 = 1 0 k g ⋅ m / s 2 = 1 0 막대의 무게:4 k g × 10 m / s 2 = 40 k g ⋅ m / s 2 = 40 4 k g × 1 0 m / s 2 = 4 0 k g ⋅ m / s 2 = 4 0
받침대가 막대를 떠받치는 힘의 크기를 F F
막대에 작용하는 알짜힘이 0 0 F = 10 M m / s 2 + 40 N + 10 N , F = 1 0 M m / s 2 + 4 0 N + 1 0 N , F = 10 M m / s 2 + 50 N F = 1 0 M m / s 2 + 5 0 N
돌림힘은 기준점으로부터 힘이 작용한 지점까지의 벡터를 r → r r → r F → F r → × F → r × F
기준점을 힘이 작용하는 지점으로 잡으면 해당 위치는 r → = 0 r = 0 10 M m / s 2 1 0 M m / s 2
A A 0 × 10 M m / s 2 = 0 0 × 1 0 M m / s 2 = 0 B B − 3 m × 10 N = − 30 − 3 m × 1 0 N = − 3 0 ( − ) ( − ) 막대의 무게에 의한 돌림힘:− 2 m × 40 N = − 80 − 2 m × 4 0 N = − 8 0 ( − ) ( − )
받침대가 막대를 떠받치는 힘에 의한 돌림힘:1 m × F = F 1 m × F = F ( + ) ( + )
막대에 작용하는 돌림힘의 합이 0 0 0 − 30 N ⋅ m − 80 N ⋅ m + F m = 0 0 − 3 0 N ⋅ m − 8 0 N ⋅ m + F m = 0 − 30 N ⋅ m − 80 N ⋅ m + F m = 0 , − 3 0 N ⋅ m − 8 0 N ⋅ m + F m = 0 , − 30 N − 80 N + F = 0 , − 3 0 N − 8 0 N + F = 0 , − 110 N + F = 0 , − 1 1 0 N + F = 0 , F = 110 N F = 1 1 0 N
이를 ①에 넣으면F = 10 M m / s 2 + 50 N F = 1 0 M m / s 2 + 5 0 N 110 N = 10 M m / s 2 + 50 N , 1 1 0 N = 1 0 M m / s 2 + 5 0 N , 60 N = 10 M m / s 2 , 6 0 N = 1 0 M m / s 2 , 60 k g ⋅ m / s 2 = 10 M m / s 2 , 6 0 k g ⋅ m / s 2 = 1 0 M m / s 2 , 60 k g = 10 M , 6 0 k g = 1 0 M , M = 6 k g M = 6 k g
∘ ∘
막대에 받침대가 1 1 A A B B
막대에 작용하는 F 알짜 = 0 F 알짜 = 0 0 0
막대, A A B B 1 1 2 2 3 3 m 1 = 4 k g m 1 = 4 k g m 2 = M m 2 = M m 3 = 1 k g m 3 = 1 k g
따라서 ∑ i = 1 n m i = ∑ i = 1 3 m i = m 1 + m 2 + m 3 = 4 k g + M + 1 k g = M + 5 k g i = 1 ∑ n m i = i = 1 ∑ 3 m i = m 1 + m 2 + m 3 = 4 k g + M + 1 k g = M + 5 k g
A A r 1 = 2 m r 1 = 2 m r 2 = 0 r 2 = 0 r 3 = 3 m r 3 = 3 m
그러므로 ∑ i = 1 n m i r i = ∑ i = 1 3 m i r i , i = 1 ∑ n m i r i = i = 1 ∑ 3 m i r i , ∑ i = 1 n m i r i = m 1 r 1 + m 2 r 2 + m 3 r 3 , i = 1 ∑ n m i r i = m 1 r 1 + m 2 r 2 + m 3 r 3 , ∑ i = 1 n m i r i = ( 4 k g × 2 m ) + ( M × 0 ) + ( 1 k g × 3 m ) , i = 1 ∑ n m i r i = ( 4 k g × 2 m ) + ( M × 0 ) + ( 1 k g × 3 m ) , ∑ i = 1 n m i r i = 8 k g ⋅ m + 0 + 3 k g ⋅ m , i = 1 ∑ n m i r i = 8 k g ⋅ m + 0 + 3 k g ⋅ m , ∑ i = 1 n m i r i = 11 k g ⋅ m i = 1 ∑ n m i r i = 1 1 k g ⋅ m
∑ i = 1 n m i r i ∑ i = 1 n m i = ∑ i = 1 3 m i r i ∑ i = 1 3 m i = 11 k g ⋅ m M + 5 k g = 1 m i = 1 ∑ n m i i = 1 ∑ n m i r i = i = 1 ∑ 3 m i i = 1 ∑ 3 m i r i = M + 5 k g 1 1 k g ⋅ m = 1 m 11 k g ⋅ m M + 5 k g = 1 m , M + 5 k g 1 1 k g ⋅ m = 1 m , 11 k g M + 5 k g = 1 , M + 5 k g 1 1 k g = 1 , 11 k g = M + 5 k g , 1 1 k g = M + 5 k g , M = 6 k g M = 6 k g
막대에 작용하는 알짜힘이 0 0 ( 4 k g + 6 k g + 1 k g ) × 10 m / s 2 , ( 4 k g + 6 k g + 1 k g ) × 1 0 m / s 2 , 11 k g × 10 m / s 2 , 1 1 k g × 1 0 m / s 2 , 110 k g ⋅ m / s 2 = 110 N 1 1 0 k g ⋅ m / s 2 = 1 1 0 N
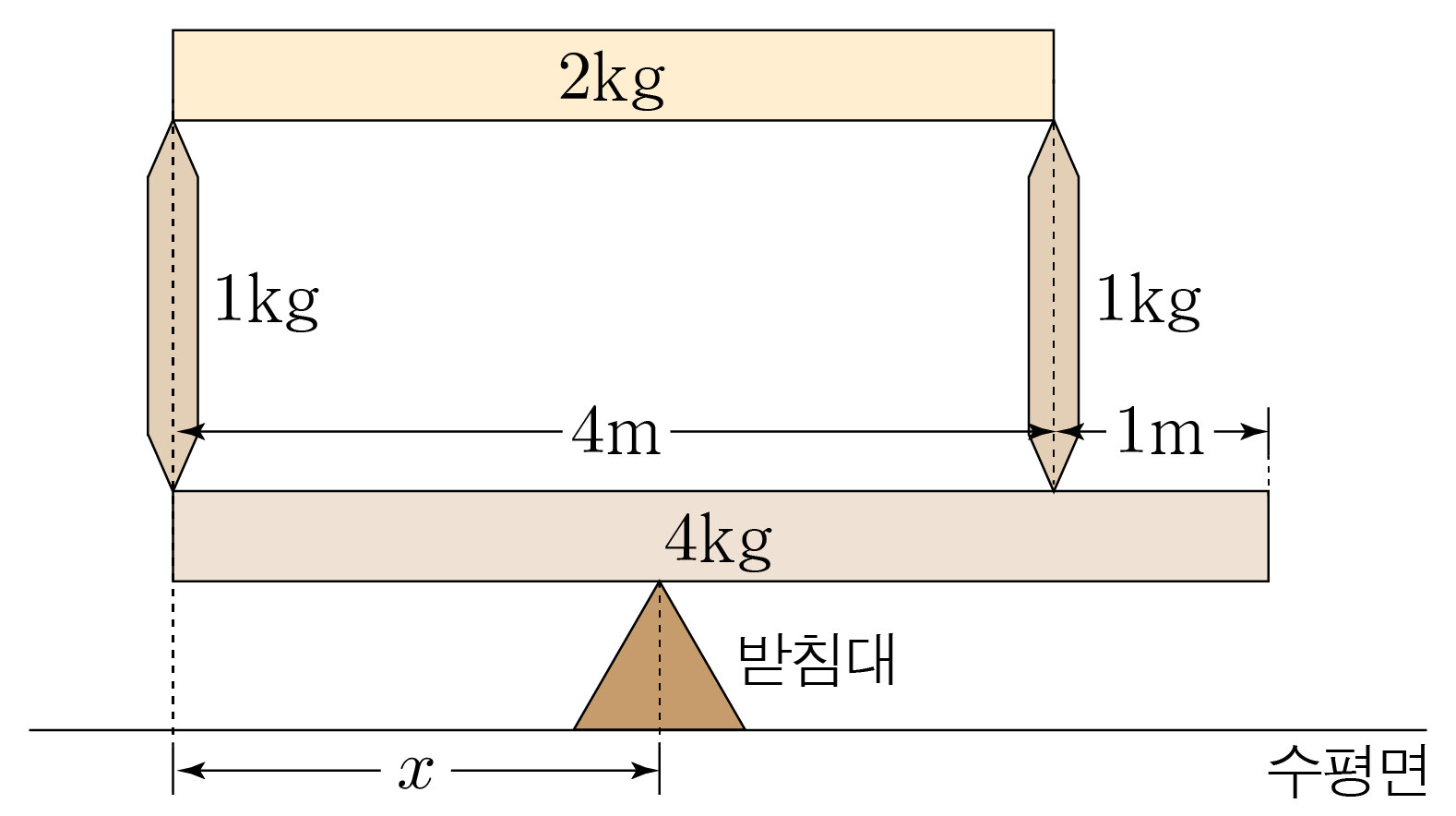
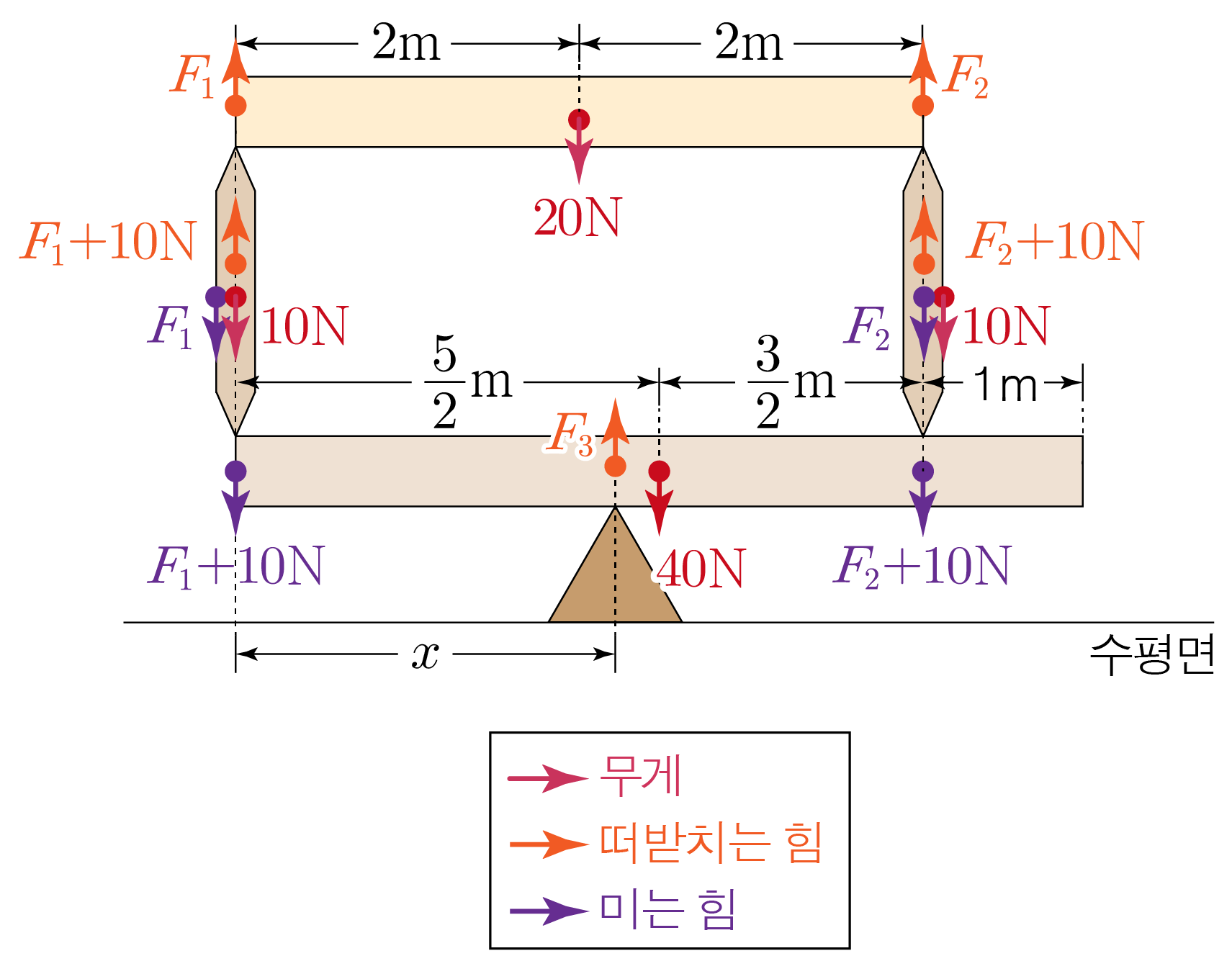
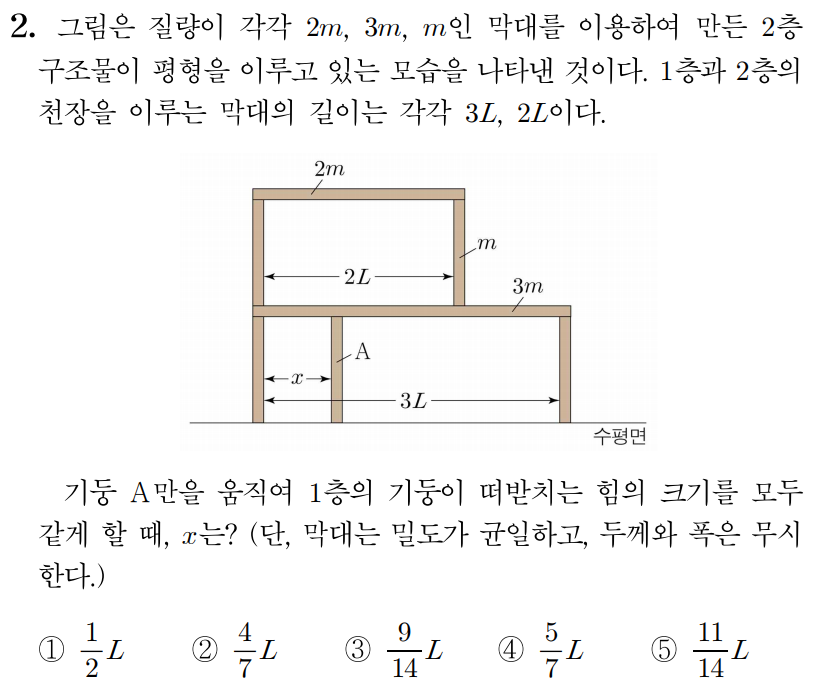
그림은 질량이 각각 2 k g 2 k g 4 k g 4 k g 1 k g 1 k g 4 m 4 m 5 m 5 m x x 10 m / s 2 1 0 m / s 2
∘ ∘
기둥과 막대의 무게를 구하면 아래와 같다.
기둥의 무게:1 k g × 10 m / s 2 = 10 k g ⋅ m / s 2 = 10 1 k g × 1 0 m / s 2 = 1 0 k g ⋅ m / s 2 = 1 0
위쪽 막대의 무게:2 k g × 10 m / s 2 = 20 k g ⋅ m / s 2 = 20 2 k g × 1 0 m / s 2 = 2 0 k g ⋅ m / s 2 = 2 0
아래쪽 막대의 무게:4 k g × 10 m / s 2 = 40 k g ⋅ m / s 2 = 40 4 k g × 1 0 m / s 2 = 4 0 k g ⋅ m / s 2 = 4 0
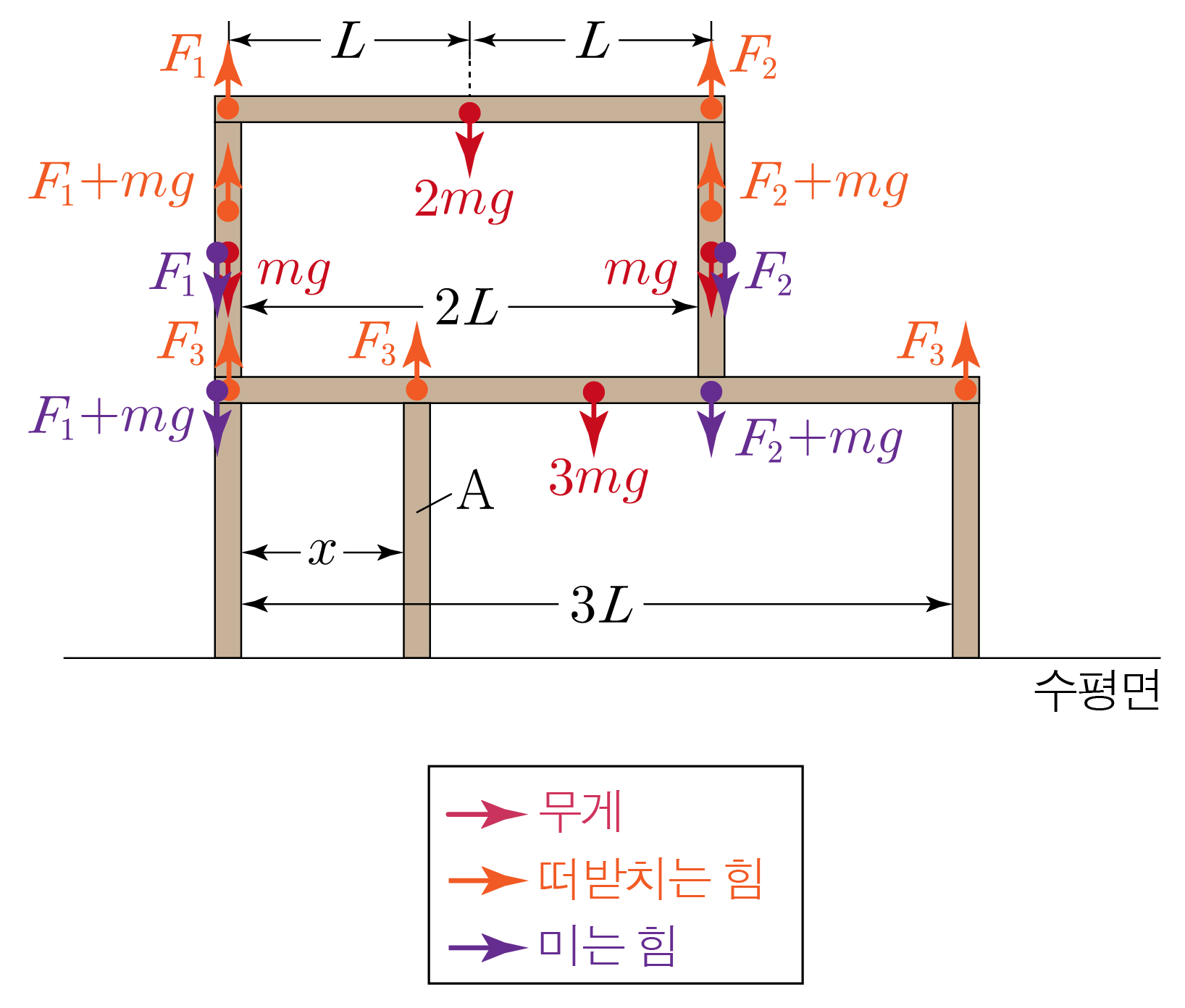
작용·반작용 법칙에 의해 기둥이 막대를 떠받치는 힘은 막대가 기둥을 미는 힘과 크기는 같고 방향은 반대이다.F 1 F 1 F 2 F 2 F 1 + 10 N F 1 + 1 0 N F 2 + 10 N F 2 + 1 0 N
그러므로 받침대가 막대를 떠받치는 힘의 크기를 F 3 F 3
위쪽과 아래쪽 막대에 작용하는 알짜힘이 0 0 F 1 + F 2 = 20 N F 1 + F 2 = 2 0 N F 3 = F 1 + 10 N + 40 N + F 2 + 10 N , F 3 = F 1 + 1 0 N + 4 0 N + F 2 + 1 0 N , F 3 = F 1 + F 2 + 60 N F 3 = F 1 + F 2 + 6 0 N
①에서 F 1 + F 2 = 20 N F 1 + F 2 = 2 0 N F 3 = 20 N + 60 N = 80 N F 3 = 2 0 N + 6 0 N = 8 0 N 1. 1 .
위쪽 막대에서 F 1 F 1
F 1 F 1 0 × F 1 = 0 0 × F 1 = 0 F 2 F 2 4 m × F 2 = 4 F 2 4 m × F 2 = 4 F 2 위쪽 막대의 무게에 의한 돌림힘:− 2 m × 20 N = − 40 − 2 m × 2 0 N = − 4 0
위쪽 막대에 작용하는 돌림힘의 합이 0 0 0 + 4 F 2 m − 40 N ⋅ m = 0 0 + 4 F 2 m − 4 0 N ⋅ m = 0 4 F 2 m − 40 N ⋅ m = 0 , 4 F 2 m − 4 0 N ⋅ m = 0 , 4 F 2 m = 40 N ⋅ m , 4 F 2 m = 4 0 N ⋅ m , 4 F 2 = 40 N , 4 F 2 = 4 0 N , F 2 = 10 N F 2 = 1 0 N
이를 ①에 넣으면F 1 + F 2 = 20 N F 1 + F 2 = 2 0 N F 1 + 10 N = 20 N , F 1 + 1 0 N = 2 0 N , F 1 = 10 N F 1 = 1 0 N 2. 2 .
F 1 = 10 N F 1 = 1 0 N F 2 = 10 N F 2 = 1 0 N F 3 = 80 N F 3 = 8 0 N
아래쪽 막대의 가장 왼쪽 지점을 기준점으로 할 때, 아래쪽 막대에 작용하는 돌림힘을 구하면 아래와 같다.
왼쪽 기둥이 미는 힘에 의한 돌림힘:0 × 20 N = 0 0 × 2 0 N = 0
오른쪽 기둥이 미는 힘에 의한 돌림힘:− 4 m × 20 N = − 80 − 4 m × 2 0 N = − 8 0
아래쪽 막대의 무게에 의한 돌림힘:− 5 2 m × 40 N = − 100 − 2 5 m × 4 0 N = − 1 0 0
받침대가 막대를 떠받치는 힘에 의한 돌림힘:x × 80 N = 80 x x × 8 0 N = 8 0 x
아래쪽 막대에 작용하는 돌림힘의 합이 0 0 0 − 80 N ⋅ m − 100 N ⋅ m + 80 x N = 0 0 − 8 0 N ⋅ m − 1 0 0 N ⋅ m + 8 0 x N = 0 − 80 N ⋅ m − 100 N ⋅ m + 80 x N = 0 , − 8 0 N ⋅ m − 1 0 0 N ⋅ m + 8 0 x N = 0 , − 80 m − 100 m + 80 x = 0 , − 8 0 m − 1 0 0 m + 8 0 x = 0 , − 180 m + 80 x = 0 , − 1 8 0 m + 8 0 x = 0 , 80 x = 180 m , 8 0 x = 1 8 0 m , x = 180 80 m = 18 8 m = 9 4 m x = 8 0 1 8 0 m = 8 1 8 m = 4 9 m
∘ ∘
아래쪽 막대에 받침대가 1 1
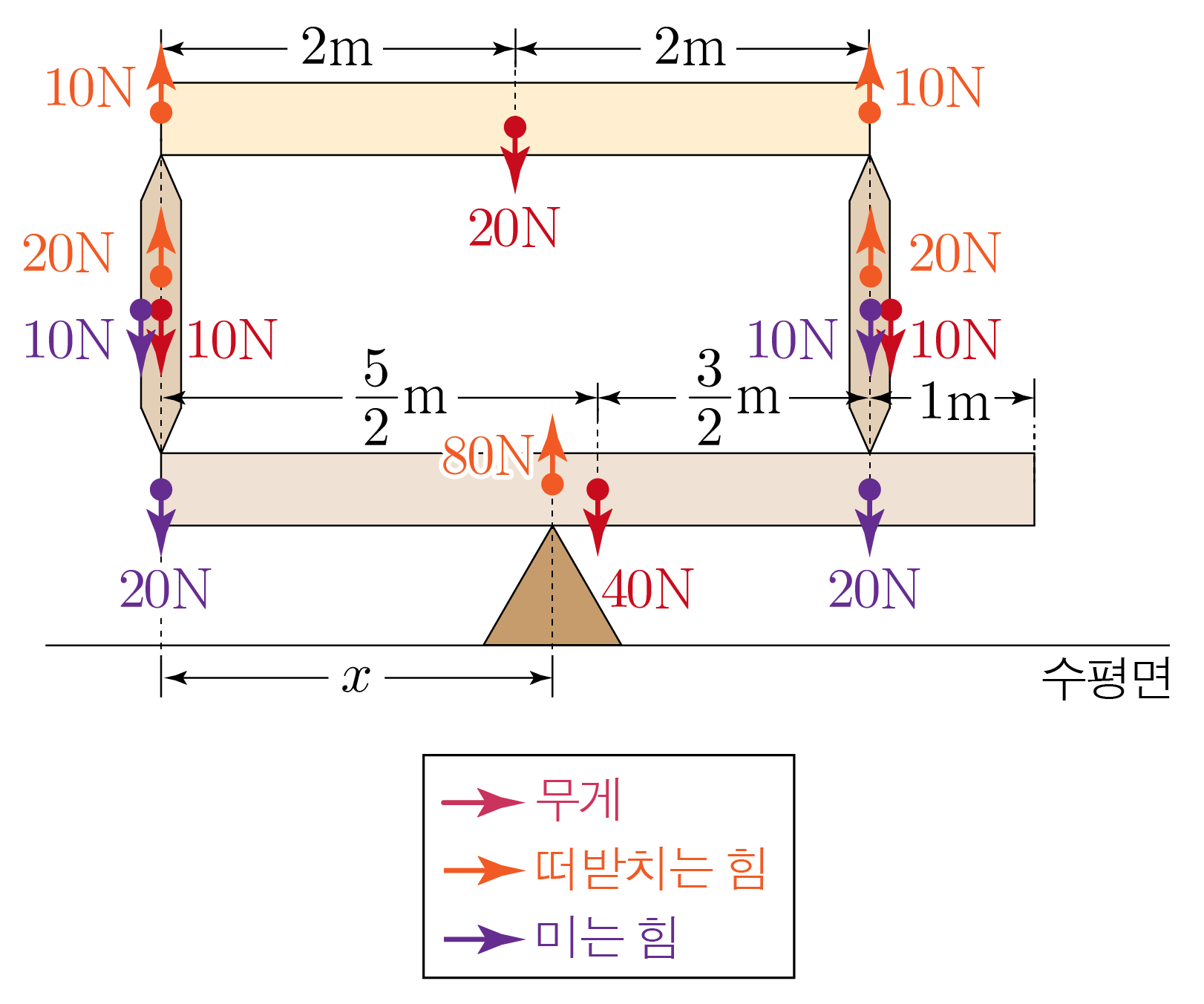
각 막대에 작용하는 중력은 수평면에 수직인 방향으로 작용하는 벡터이므로, 각 막대의 질량 중심의 위치가 수평면에 수평인 직선 상에 놓여 있는 것으로 생각할 수 있다.
위쪽 막대, 아래쪽 막대, 왼쪽 기둥, 오른쪽 기둥을 각각 1 1 2 2 3 3 4 4 m 1 = 2 k g m 1 = 2 k g m 2 = 4 k g m 2 = 4 k g m 3 = 1 k g m 3 = 1 k g m 4 = 1 k g m 4 = 1 k g
따라서 ∑ i = 1 n m i = ∑ i = 1 4 m i = m 1 + m 2 + m 3 + m 4 = 2 k g + 4 k g + 1 k g + 1 k g = 8 k g i = 1 ∑ n m i = i = 1 ∑ 4 m i = m 1 + m 2 + m 3 + m 4 = 2 k g + 4 k g + 1 k g + 1 k g = 8 k g
아래쪽 막대의 가장 왼쪽 지점을 기준점이라 하면 r 1 = 2 m r 1 = 2 m r 2 = 5 2 m r 2 = 2 5 m r 3 = 0 r 3 = 0 r 4 = 4 m r 4 = 4 m
그러므로 ∑ i = 1 n m i r i = ∑ i = 1 4 m i r i , i = 1 ∑ n m i r i = i = 1 ∑ 4 m i r i , ∑ i = 1 n m i r i = m 1 r 1 + m 2 r 2 + m 3 r 3 + m 4 r 4 , i = 1 ∑ n m i r i = m 1 r 1 + m 2 r 2 + m 3 r 3 + m 4 r 4 , ∑ i = 1 n m i r i i = 1 ∑ n m i r i = ( 2 k g × 2 m ) + ( 4 k g × 5 2 m ) + ( 1 k g × 0 ) + ( 1 k g × 4 m ) , = ( 2 k g × 2 m ) + ( 4 k g × 2 5 m ) + ( 1 k g × 0 ) + ( 1 k g × 4 m ) , ∑ i = 1 n m i r i = 4 k g ⋅ m + 10 k g ⋅ m + 0 + 4 k g ⋅ m , i = 1 ∑ n m i r i = 4 k g ⋅ m + 1 0 k g ⋅ m + 0 + 4 k g ⋅ m , ∑ i = 1 n m i r i = 18 k g ⋅ m i = 1 ∑ n m i r i = 1 8 k g ⋅ m
∑ i = 1 n m i r i ∑ i = 1 n m i = ∑ i = 1 4 m i r i ∑ i = 1 4 m i = 18 k g ⋅ m 8 k g = 18 m 8 = 9 4 m i = 1 ∑ n m i i = 1 ∑ n m i r i = i = 1 ∑ 4 m i i = 1 ∑ 4 m i r i = 8 k g 1 8 k g ⋅ m = 8 1 8 m = 4 9 m x = 9 4 m x = 4 9 m
1번 문항 정답 및 해설 보기
정답: $4$
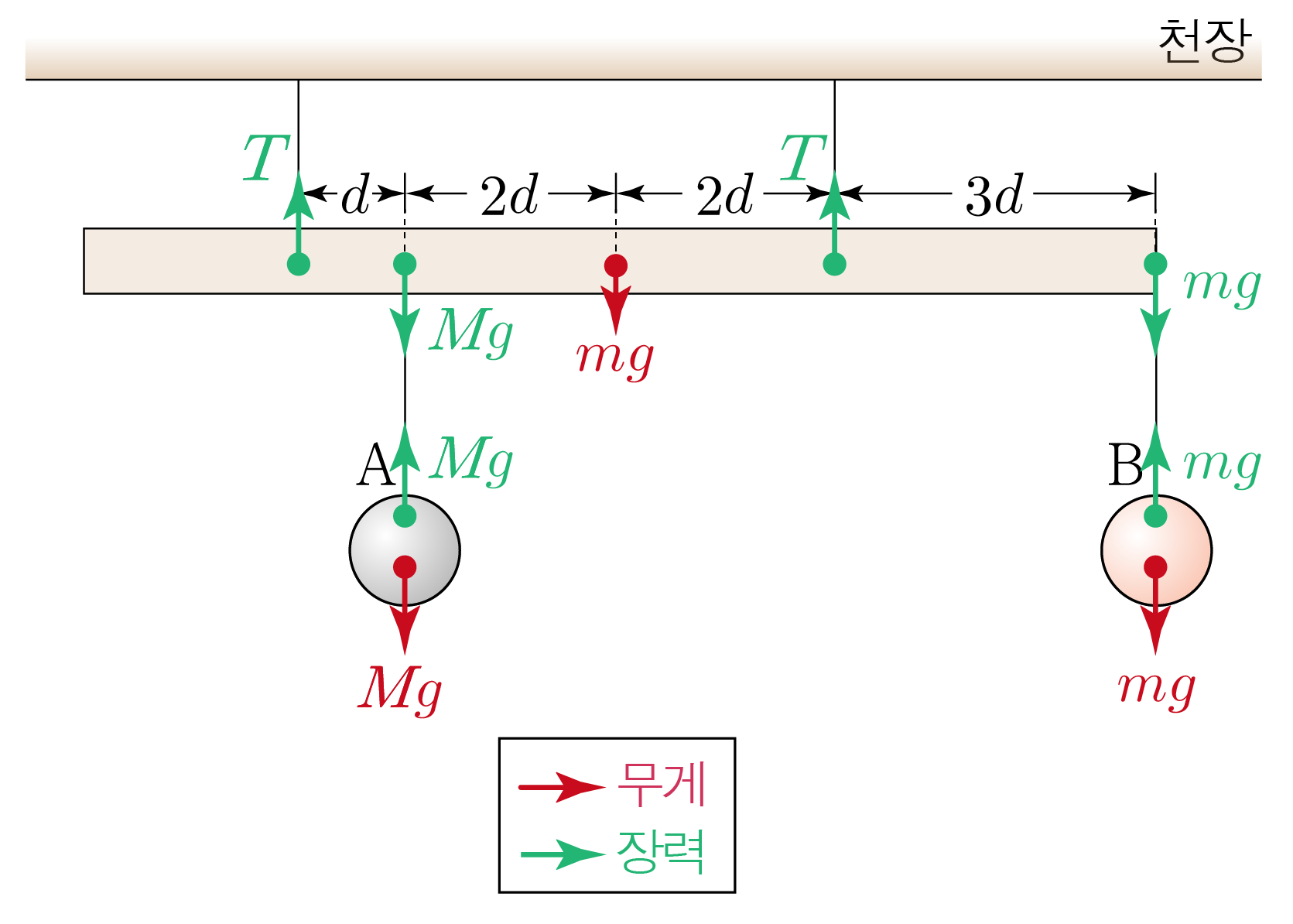
막대와 물체의 무게를 구하면 아래와 같다.
막대의 무게: m g m g
A A M g M g B B m g m g
천장과 연결된 실이 막대를 당기는 힘의 크기를 T T
막대에 작용하는 알짜힘이 0 0 2 T = M g + m g + m g , 2 T = M g + m g + m g , 2 T = M g + 2 m g 2 T = M g + 2 m g
막대에서 천장과 연결된 왼쪽 실이 막대에 힘을 작용하는 지점을 기준점으로 할 때, 막대에 작용하는 돌림힘을 구하면 아래와 같다.
천장과 연결된 왼쪽 실이 당기는 힘에 의한 돌림힘:0 × T = 0 0 × T = 0
천장과 연결된 오른쪽 실이 당기는 힘에 의한 돌림힘:5 d × T = 5 d T 5 d × T = 5 d T
막대의 무게에 의한 돌림힘:− 3 d × m g = − 3 d m g − 3 d × m g = − 3 d m g
A A − d × M g = − d M g − d × M g = − d M g B B − 8 d × m g = − 8 d m g − 8 d × m g = − 8 d m g
막대에 작용하는 돌림힘의 합이 0 0 0 + 5 d T − 3 d m g − d M g − 8 d m g = 0 0 + 5 d T − 3 d m g − d M g − 8 d m g = 0 5 d T − 3 d m g − d M g − 8 d m g = 0 , 5 d T − 3 d m g − d M g − 8 d m g = 0 , 5 T − 3 m g − M g − 8 m g = 0 , 5 T − 3 m g − M g − 8 m g = 0 , 5 T − 11 m g − M g = 0 , 5 T − 1 1 m g − M g = 0 , 5 T = 11 m g + M g , 5 T = 1 1 m g + M g , T = 11 5 m g + 1 5 M g T = 5 1 1 m g + 5 1 M g
이를 ①에 넣으면2 T = M g + 2 m g 2 T = M g + 2 m g 2 × ( 11 5 m g + 1 5 M g ) = M g + 2 m g , 2 × ( 5 1 1 m g + 5 1 M g ) = M g + 2 m g , 22 5 m g + 2 5 M g = M g + 2 m g , 5 2 2 m g + 5 2 M g = M g + 2 m g , 22 5 m + 2 5 M = M + 2 m , 5 2 2 m + 5 2 M = M + 2 m , 12 5 m = 3 5 M , 5 1 2 m = 5 3 M , 12 m = 3 M , 1 2 m = 3 M , M = 4 m M = 4 m
따라서 정답은 4 4
2번 문항 정답 및 해설 보기
정답: $3$
막대의 무게를 구하면 아래와 같다.
질량이 m m m g m g
질량이 2 m 2 m 2 m g 2 m g
질량이 3 m 3 m 3 m g 3 m g
질량이 m m
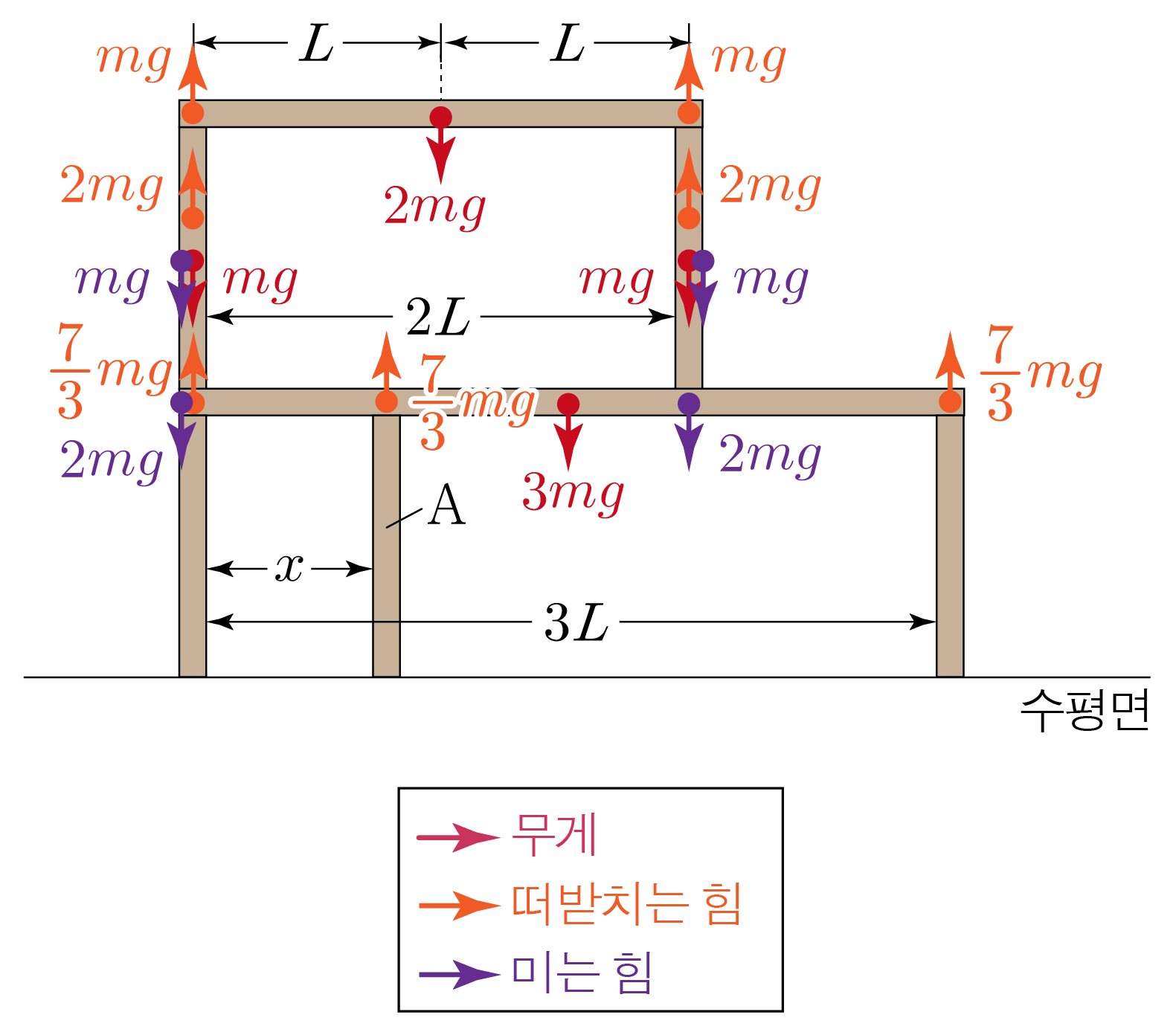
작용·반작용 법칙에 의해 기둥이 막대를 떠받치는 힘은 막대가 기둥을 미는 힘과 크기는 같고 방향은 반대이다.2 2 F 1 F 1 F 2 F 2 2 2 F 1 + m g F 1 + m g F 2 + m g F 2 + m g
그러므로 1 1 F 3 F 3 2 2
위쪽과 아래쪽 막대에 작용하는 알짜힘이 0 0 F 1 + F 2 = 2 m g F 1 + F 2 = 2 m g 3 F 3 = F 1 + m g + 3 m g + F 2 + m g , 3 F 3 = F 1 + m g + 3 m g + F 2 + m g , 3 F 3 = F 1 + F 2 + 5 m g 3 F 3 = F 1 + F 2 + 5 m g
①에서 F 1 + F 2 = 2 m g F 1 + F 2 = 2 m g 3 F 3 = 2 m g + 5 m g = 7 m g , 3 F 3 = 2 m g + 5 m g = 7 m g , F 3 = 7 3 m g F 3 = 3 7 m g
1. 1 .
위쪽 막대에서 F 1 F 1
F 1 F 1 0 × F 1 = 0 0 × F 1 = 0 F 2 F 2 2 L × F 2 = 2 L F 2 2 L × F 2 = 2 L F 2 위쪽 막대의 무게에 의한 돌림힘:− L × 2 m g = − 2 L m g − L × 2 m g = − 2 L m g
위쪽 막대에 작용하는 돌림힘의 합이 0 0 0 + 2 L F 2 − 2 L m g = 0 0 + 2 L F 2 − 2 L m g = 0 2 L F 2 − 2 L m g = 0 , 2 L F 2 − 2 L m g = 0 , 2 F 2 − 2 m g = 0 , 2 F 2 − 2 m g = 0 , 2 F 2 = 2 m g , 2 F 2 = 2 m g , F 2 = m g F 2 = m g
이를 ①에 넣으면F 1 + F 2 = 2 m g F 1 + F 2 = 2 m g F 1 + m g = 2 m g , F 1 + m g = 2 m g , F 1 = m g F 1 = m g
2. 2 .
F 1 = m g , F 2 = m g , F 3 = 7 3 m g F 1 = m g , F 2 = m g , F 3 = 3 7 m g 2 2
아래쪽 막대의 가장 왼쪽 지점을 기준점으로 할 때, 아래쪽 막대에 작용하는 돌림힘을 구하면 아래와 같다.
2 2 0 × 2 m g = 0 0 × 2 m g = 0 2 2 − 2 L × 2 m g = − 4 L m g − 2 L × 2 m g = − 4 L m g 아래쪽 막대의 무게에 의한 돌림힘:− 3 2 L × 3 m g = − 9 2 L m g − 2 3 L × 3 m g = − 2 9 L m g
1 1 0 × 7 3 m g = 0 0 × 3 7 m g = 0 A A x × 7 3 m g = 7 3 x m g x × 3 7 m g = 3 7 x m g 1 1 3 L × 7 3 m g = 7 L m g 3 L × 3 7 m g = 7 L m g
아래쪽 막대에 작용하는 돌림힘의 합이 0 0 0 − 4 L m g − 9 2 L m g + 0 + 7 3 x m g + 7 L m g = 0 0 − 4 L m g − 2 9 L m g + 0 + 3 7 x m g + 7 L m g = 0 − 4 L m g − 9 2 L m g + 7 3 x m g + 7 L m g = 0 , − 4 L m g − 2 9 L m g + 3 7 x m g + 7 L m g = 0 , − 4 L − 9 2 L + 7 3 x + 7 L = 0 , − 4 L − 2 9 L + 3 7 x + 7 L = 0 , − 17 2 L + 7 3 x + 7 L = 0 , − 2 1 7 L + 3 7 x + 7 L = 0 , − 3 2 L + 7 3 x = 0 , − 2 3 L + 3 7 x = 0 , 7 3 x = 3 2 L , 3 7 x = 2 3 L , x = 3 2 L × 3 7 , x = 2 3 L × 7 3 , x = 9 14 L x = 1 4 9 L
따라서 정답은 3 3