물체의 질량( m ) ( m ) ( v → ) ( v ) ( m v → ) ( m v ) k g ⋅ m / s k g ⋅ m / s p → p ( v → ) ( v )
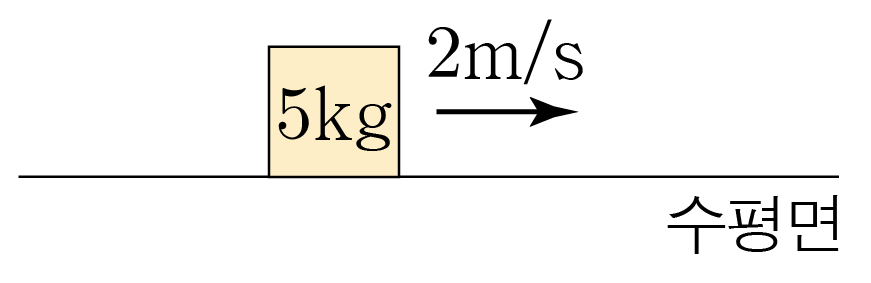
그림은 질량이 5 k g 5 k g 2 m / s 2 m / s
오른쪽 방향을 양 ( + ) ( + ) + 2 m / s + 2 m / s
운동량은 물체의 질량과 속도의 곱과 같으므로 5 k g × ( + 2 m / s ) = + 10 k g ⋅ m / s 5 k g × ( + 2 m / s ) = + 1 0 k g ⋅ m / s
충돌하는 물체의 운동량의 합은 충돌 전과 후가 같다.
아래 그림과 같이 물체 A A B B m A m A m B m B A A v A 1 v A 1 v A 2 v A 2 B B v B 1 v B 1 v B 2 v B 2 m A v A 1 + m B v B 1 = m A v A 2 + m B v B 2 m A v A 1 + m B v B 1 = m A v A 2 + m B v B 2
그림 (가)는 마찰이 없는 수평면에서 물체 A A B B v v A A B B A A B B 1 m / s 1 m / s 2 m / s 2 m / s A A B B 1 k g 1 k g 2 k g 2 k g v v
오른쪽 방향을 양( + ) ( + ) A A B B
A A 1 k g × ( + v ) = v 1 k g × ( + v ) = v B B 2 k g × 0 = 0 2 k g × 0 = 0
그러므로 충돌 전 A A B B v k g + 0 = v k g v k g + 0 = v k g
(나)에서 A A B B
A A 1 k g × ( − 1 m / s ) = − 1 1 k g × ( − 1 m / s ) = − 1 B B 2 k g × ( + 2 m / s ) = 4 2 k g × ( + 2 m / s ) = 4
그러므로 충돌 후 A A B B − 1 k g ⋅ m / s + 4 k g ⋅ m / s = 3 k g ⋅ m / s − 1 k g ⋅ m / s + 4 k g ⋅ m / s = 3 k g ⋅ m / s
운동량 보존 법칙에 의해 충돌하는 물체의 운동량의 합은 충돌 전과 후가 같으므로v k g = 3 k g ⋅ m / s , v k g = 3 k g ⋅ m / s , v = 3 m / s v = 3 m / s
그림과 같이 질량이 각각 m A m A m B m B A A B B v A 1 v A 1 v B 1 v B 1 v A 2 v A 2 v B 2 v B 2
서로 다른 두 물체가 충돌하는 과정에서 작용·반작용 법칙에 의해 A A B B B B A A A A B B F → A F A F → B F B A A B B a → A a A a → B a B t t F → A = − F → B , F A = − F B , m A a → A = − m B a → B , m A a A = − m B a B , m A ( v → A 2 − v → A 1 t ) = − m B ( v → B 2 − v → B 1 t ) , m A ( t v A 2 − v A 1 ) = − m B ( t v B 2 − v B 1 ) , m A ( v → A 2 − v → A 1 ) = − m B ( v → B 2 − v → B 1 ) , m A ( v A 2 − v A 1 ) = − m B ( v B 2 − v B 1 ) , m A ( v → A 2 − v → A 1 ) = m B ( v → B 1 − v → B 2 ) , m A ( v A 2 − v A 1 ) = m B ( v B 1 − v B 2 ) , m A v → A 2 − m A v → A 1 = m B v → B 1 − m B v → B 2 , m A v A 2 − m A v A 1 = m B v B 1 − m B v B 2 , m A v → A 2 + m B v → B 2 = m A v → A 1 + m B v → B 1 , m A v A 2 + m B v B 2 = m A v A 1 + m B v B 1 , m A v → A 1 + m B v → B 1 = m A v → A 2 + m B v → B 2 m A v A 1 + m B v B 1 = m A v A 2 + m B v B 2
이를 통해 운동량 보존 법칙이 성립함을 알 수 있다.
1번 문항 정답 및 해설 보기
정답: $5$
오른쪽 방향을 양( + ) ( + ) A A B B
A A m A × ( + 3 v ) = 3 m A v m A × ( + 3 v ) = 3 m A v B B m B × 0 = 0 m B × 0 = 0
그러므로 충돌 전 A A B B 3 m A v + 0 = 3 m A v 3 m A v + 0 = 3 m A v
(나)에서 A A B B
A A m A × ( + v ) = m A v m A × ( + v ) = m A v B B m B × ( + 3 v ) = 3 m B v m B × ( + 3 v ) = 3 m B v
그러므로 충돌 후 A A B B m A v + 3 m B v m A v + 3 m B v
운동량 보존 법칙에 의해 충돌하는 물체의 운동량의 합은 충돌 전과 후가 같으므로3 m A v = m A v + 3 m B v , 3 m A v = m A v + 3 m B v , 2 m A v = 3 m B v , 2 m A v = 3 m B v , m A m B = 3 v 2 v = 3 2 m B m A = 2 v 3 v = 2 3
따라서 정답은 5 5
2번 문항 정답 및 해설 보기
정답: $3$
오른쪽 방향을 양( + ) ( + ) A A B B
A A 1 k g × ( + 5 m / s ) = 5 1 k g × ( + 5 m / s ) = 5 B B 3 k g × ( + 1 m / s ) = 3 3 k g × ( + 1 m / s ) = 3
그러므로 충돌 전 A A B B 5 k g ⋅ m / s + 3 k g ⋅ m / s = 8 k g ⋅ m / s 5 k g ⋅ m / s + 3 k g ⋅ m / s = 8 k g ⋅ m / s
(나)에서 A A B B 1 k g + 3 k g = 4 k g 1 k g + 3 k g = 4 k g 4 k g × ( + v ) = 4 v k g 4 k g × ( + v ) = 4 v k g
운동량 보존 법칙에 의해 충돌하는 물체의 운동량의 합은 충돌 전과 후가 같으므로8 k g ⋅ m / s = 4 v k g , 8 k g ⋅ m / s = 4 v k g , 2 k g ⋅ m / s = v k g , 2 k g ⋅ m / s = v k g , v = 2 m / s v = 2 m / s
따라서 정답은 3 3