x y x y 2 2 x x y y
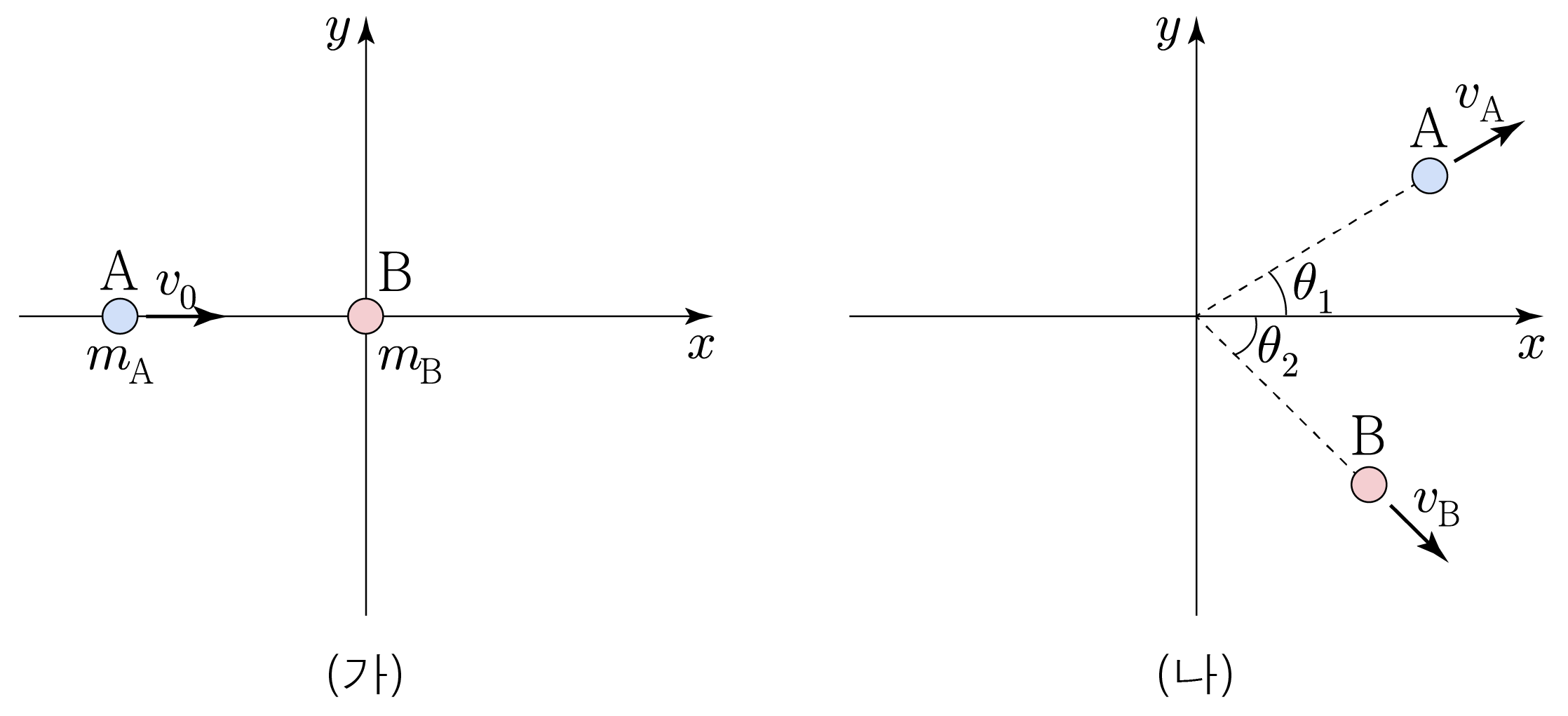
그림 (가)는 마찰이 없고 수평인 x y x y A A B B x x v 0 v 0 A A B B x x θ 1 θ 1 θ 2 θ 2 v A v A v B v B A A B B m A m A m B m B
축 방향을 양( + ) ( + ) A , B A , B x , y x , y
구분
물체
$x$ 성분
$y$ 성분
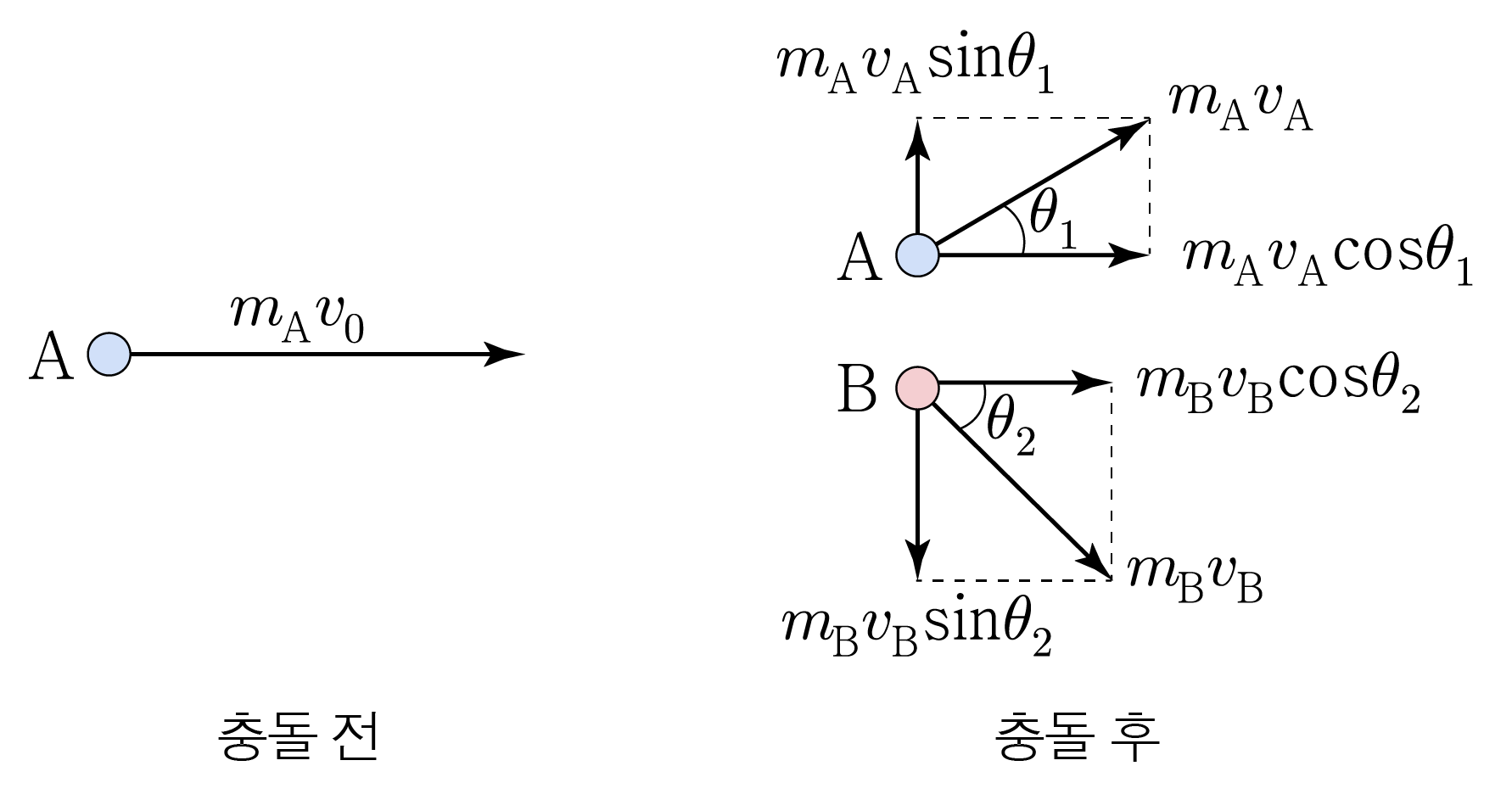
충돌 전
$\mathrm{A}$
$m_{\mathrm{A}} v_0$
$0$
$\mathrm{B}$
$0$
$0$
충돌 후
$\mathrm{A}$
$m_{\mathrm{A}} v_{\mathrm{A}} \cos \theta_1$
$m_{\mathrm{A}} v_{\mathrm{A}} \sin \theta_1$
$\mathrm{B}$
$m_{\mathrm{B}} v_{\mathrm{B}} \cos \theta_2$
$- m_{\mathrm{B}} v_{\mathrm{B}} \sin \theta_2$
운동량 보존 법칙을 x x y y
x x m A v 0 = m A v A cos θ 1 + m B v B cos θ 2 m A v 0 = m A v A cos θ 1 + m B v B cos θ 2
y y 0 = m A v A sin θ 1 − m B v B sin θ 2 0 = m A v A sin θ 1 − m B v B sin θ 2
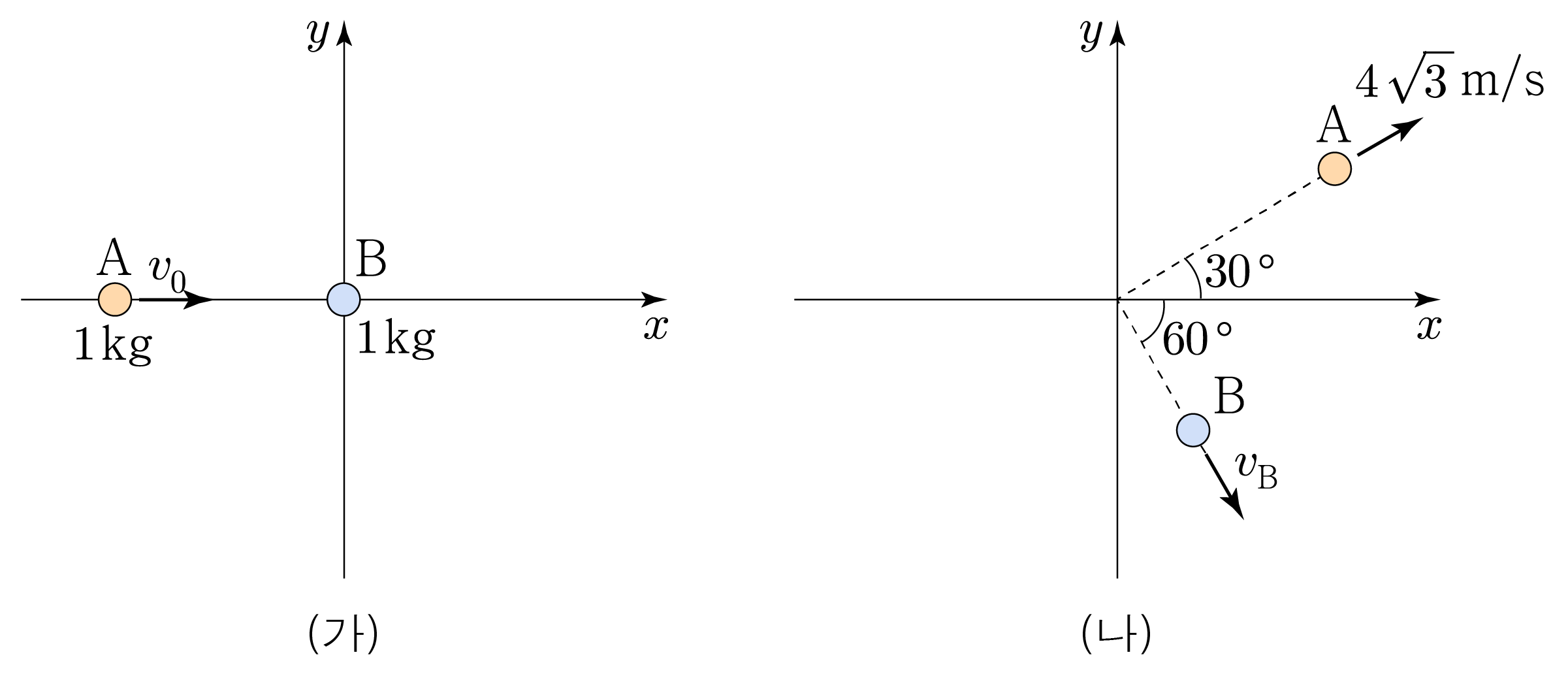
그림 (가)는 마찰이 없고 수평인 x y x y A A B B x x v 0 v 0 A A B B A A B B x x 3 0 ∘ 3 0 ∘ 6 0 ∘ 6 0 ∘ 4 3 m / s 4 3 m / s v B v B A A B B 1 k g 1 k g v 0 v 0 v B v B
축 방향을 양( + ) ( + ) A , B A , B x , y x , y
구분
물체
$x$ 성분
$y$ 성분
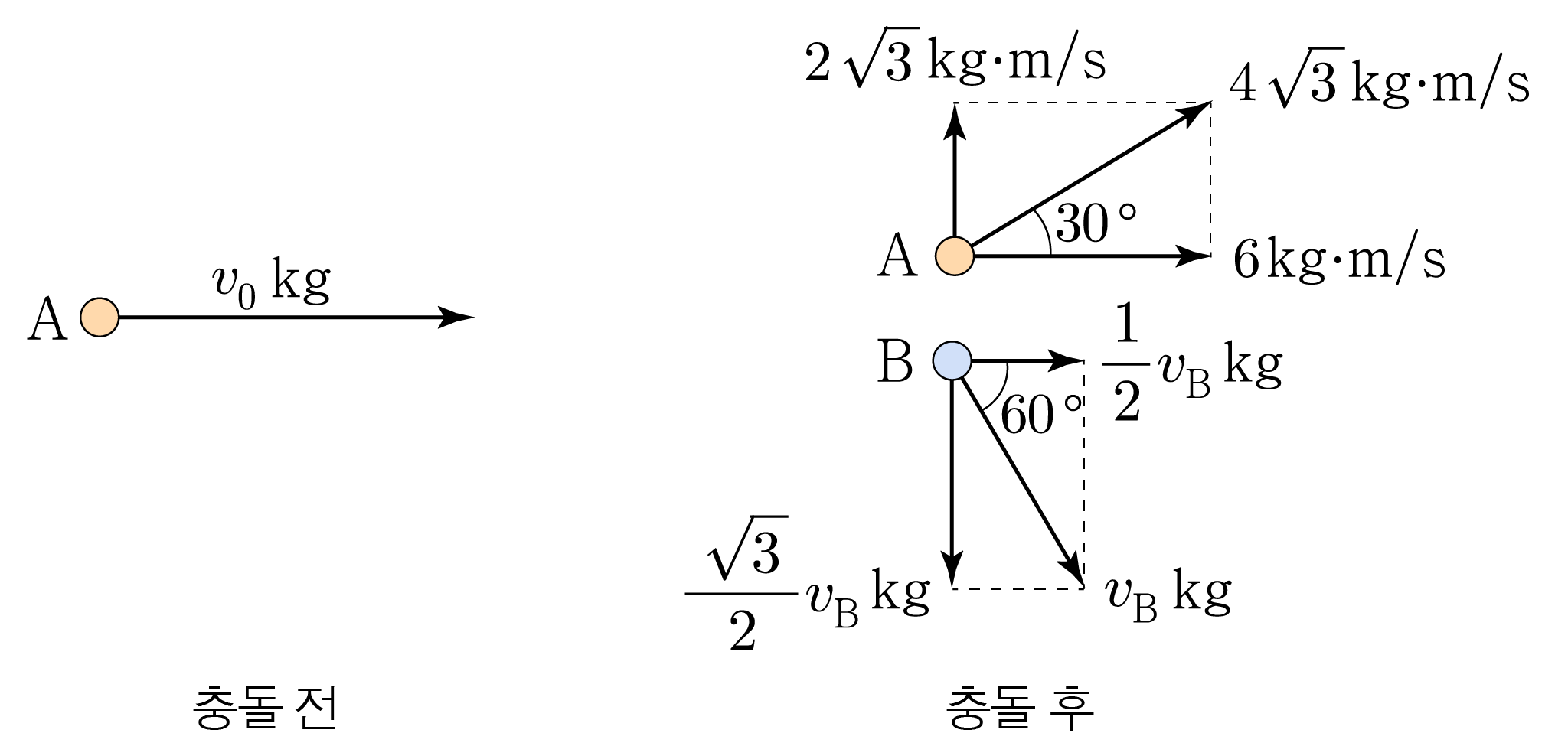
충돌 전
$\mathrm{A}$
$v_0\,\mathrm{kg}$
$0$
$\mathrm{B}$
$0$
$0$
충돌 후
$\mathrm{A}$
$4\sqrt{3}\,\mathrm{kg·m/s}\times \cos 30^\circ$
$4\sqrt{3}\,\mathrm{kg·m/s}\times \sin 30^\circ$
$\mathrm{B}$
$v_{\mathrm{B}}\,\mathrm{kg}\times \cos 60^\circ$
$-v_{\mathrm{B}}\,\mathrm{kg}\times \sin 60^\circ$
운동량 보존 법칙을 x x y y
x x v 0 k g = 6 k g ⋅ m / s + 1 2 v B k g v 0 k g = 6 k g ⋅ m / s + 2 1 v B k g
y y 0 = 2 3 k g ⋅ m / s − 3 2 v B k g , 0 = 2 3 k g ⋅ m / s − 2 3 v B k g , 3 2 v B k g = 2 3 k g ⋅ m / s , 2 3 v B k g = 2 3 k g ⋅ m / s , 3 2 v B = 2 3 m / s , 2 3 v B = 2 3 m / s , v B = 4 m / s v B = 4 m / s
이를 ①에 넣으면
v 0 k g = 6 k g ⋅ m / s + 1 2 v B k g v 0 k g = 6 k g ⋅ m / s + 2 1 v B k g v 0 k g = 6 k g ⋅ m / s + 2 k g ⋅ m / s , v 0 k g = 6 k g ⋅ m / s + 2 k g ⋅ m / s , v 0 k g = 8 k g ⋅ m / s , v 0 k g = 8 k g ⋅ m / s , v 0 = 8 m / s v 0 = 8 m / s
1번 문항 정답 및 해설 보기
정답: $2$
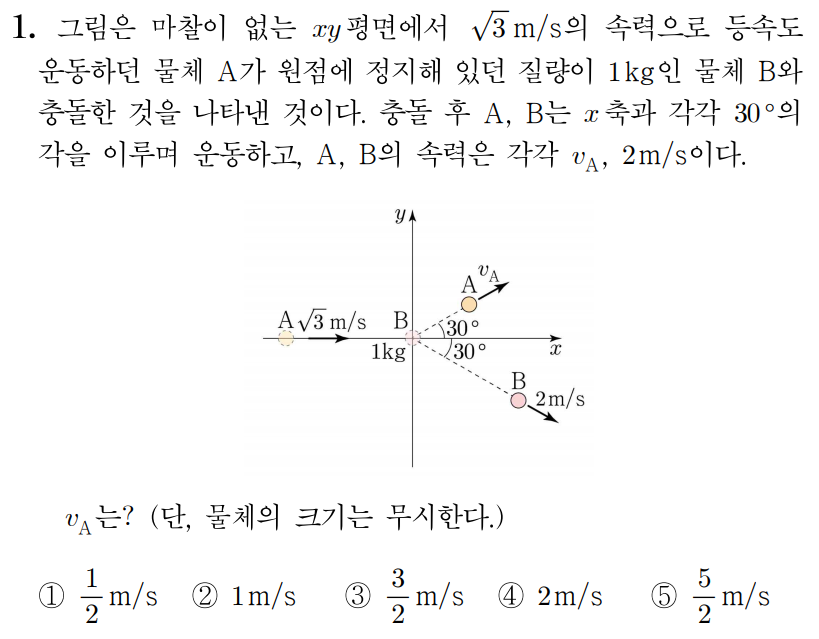
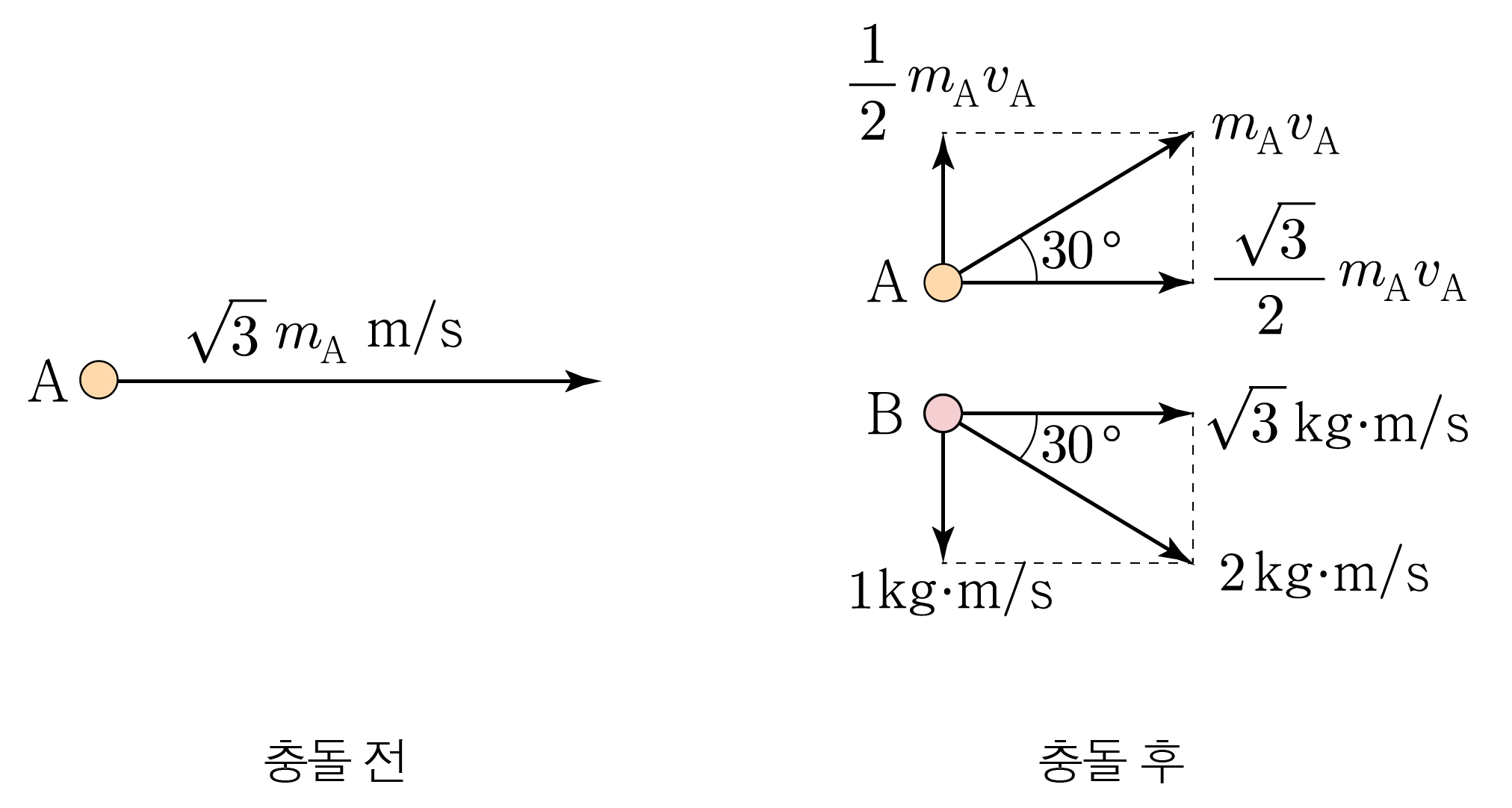
축 방향을 양( + ) ( + ) A A m A m A A , B A , B x , y x , y
구분
물체
$x$ 성분
$y$ 성분
충돌 전
$\mathrm{A}$
$\sqrt{3} m_{\mathrm{A}} \,\mathrm{m/s}$
$0$
$\mathrm{B}$
$0$
$0$
충돌 후
$\mathrm{A}$
$m_{\mathrm{A}} v_{\mathrm{A}} \times \cos 30^\circ$
$m_{\mathrm{A}} v_{\mathrm{A}} \times \sin 30^\circ$
$\mathrm{B}$
$2\,\mathrm{kg·m/s} \times \cos 30^\circ$
$-2\,\mathrm{kg·m/s} \times \sin 30^\circ$
운동량 보존 법칙을 x x y y
x x 3 m A m / s = 3 2 m A v A + 3 k g ⋅ m / s 3 m A m / s = 2 3 m A v A + 3 k g ⋅ m / s
y y 0 = 1 2 m A v A − 1 k g ⋅ m / s , 0 = 2 1 m A v A − 1 k g ⋅ m / s , 1 2 m A v A = 1 k g ⋅ m / s , 2 1 m A v A = 1 k g ⋅ m / s , m A v A = 2 k g ⋅ m / s m A v A = 2 k g ⋅ m / s
이를 ①에 넣으면3 m A m / s = 3 2 m A v A + 3 k g ⋅ m / s 3 m A m / s = 2 3 m A v A + 3 k g ⋅ m / s 3 m A m / s = 3 k g ⋅ m / s + 3 k g ⋅ m / s , 3 m A m / s = 3 k g ⋅ m / s + 3 k g ⋅ m / s , 3 m A m / s = 2 3 k g ⋅ m / s , 3 m A m / s = 2 3 k g ⋅ m / s , 3 m A = 2 3 k g , 3 m A = 2 3 k g , m A = 2 k g m A = 2 k g
이를 ②에 넣으면,m A v A = 2 k g ⋅ m / s m A v A = 2 k g ⋅ m / s 2 k g × v A = 2 k g ⋅ m / s , 2 k g × v A = 2 k g ⋅ m / s , 2 v A = 2 m / s , 2 v A = 2 m / s , v A = 1 m / s v A = 1 m / s
따라서 정답은 2 2
2번 문항 정답 및 해설 보기
정답: $2$
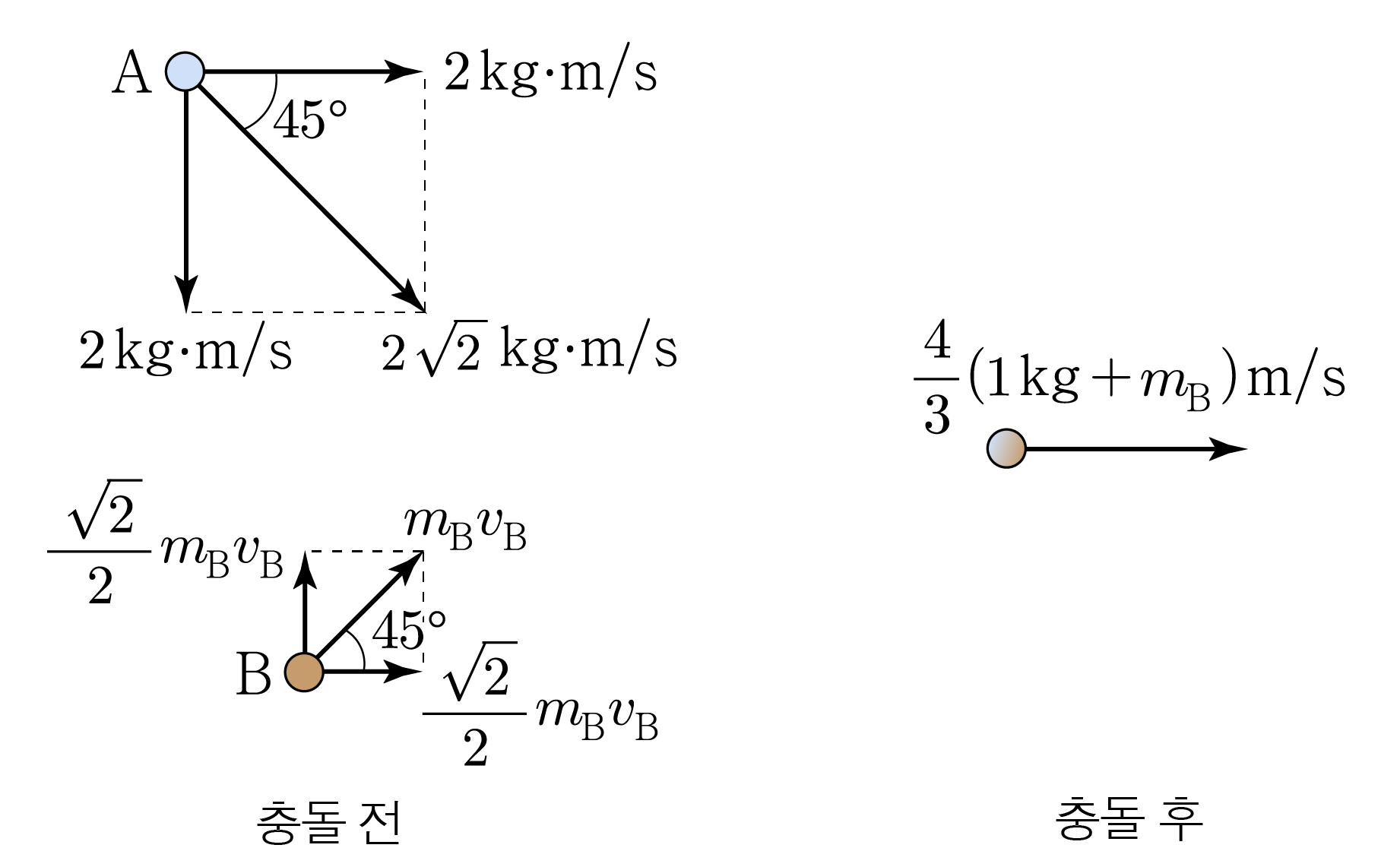
축 방향을 양( + ) ( + ) B B m B m B A , B A , B x , y x , y
구분
물체
$x$ 성분
$y$ 성분
충돌 전
$\mathrm{A}$
$2\sqrt{2}\,\mathrm{kg·m/s}\times\cos 45^\circ$
$-2\sqrt{2}\,\mathrm{kg·m/s}\times\sin 45^\circ$
$\mathrm{B}$
$m_{\mathrm{B}} v_{\mathrm{B}}\times\cos 45^\circ$
$m_{\mathrm{B}} v_{\mathrm{B}}\times\sin 45^\circ$
충돌 후
$\mathrm{A}$와 $\mathrm{B}$가 합쳐진 덩어리
$\frac{4}{3}\left(1\,\mathrm{kg}+m_{\mathrm{B}}\right)\,\mathrm{m/s}$
$0$
운동량 보존 법칙을 x x y y
x x 2 k g ⋅ m / s + 2 2 m B v B = 4 3 ( 1 k g + m B ) m / s 2 k g ⋅ m / s + 2 2 m B v B = 3 4 ( 1 k g + m B ) m / s
y y − 2 k g ⋅ m / s + 2 2 m B v B = 0 , − 2 k g ⋅ m / s + 2 2 m B v B = 0 , 2 2 m B v B = 2 k g ⋅ m / s , 2 2 m B v B = 2 k g ⋅ m / s , m B v B = 2 2 k g ⋅ m / s m B v B = 2 2 k g ⋅ m / s
이를 ①에 넣으면2 k g ⋅ m / s + 2 2 m B v B = 4 3 ( 1 k g + m B ) m / s 2 k g ⋅ m / s + 2 2 m B v B = 3 4 ( 1 k g + m B ) m / s 2 k g ⋅ m / s + 2 2 × 2 2 k g ⋅ m / s = 4 3 ( 1 k g + m B ) m / s , 2 k g ⋅ m / s + 2 2 × 2 2 k g ⋅ m / s = 3 4 ( 1 k g + m B ) m / s , 2 k g ⋅ m / s + 2 k g ⋅ m / s = 4 3 ( 1 k g + m B ) m / s , 2 k g ⋅ m / s + 2 k g ⋅ m / s = 3 4 ( 1 k g + m B ) m / s , 4 k g ⋅ m / s = 4 3 ( 1 k g + m B ) m / s , 4 k g ⋅ m / s = 3 4 ( 1 k g + m B ) m / s , 4 k g = 4 3 ( 1 k g + m B ) , 4 k g = 3 4 ( 1 k g + m B ) , 3 k g = 1 k g + m B , 3 k g = 1 k g + m B , m B = 2 k g m B = 2 k g
이를 ②에 넣으면m B v B = 2 2 k g ⋅ m / s m B v B = 2 2 k g ⋅ m / s 2 k g × v B = 2 2 k g ⋅ m / s , 2 k g × v B = 2 2 k g ⋅ m / s , v B = 2 m / s v B = 2 m / s
따라서 정답은 2 2