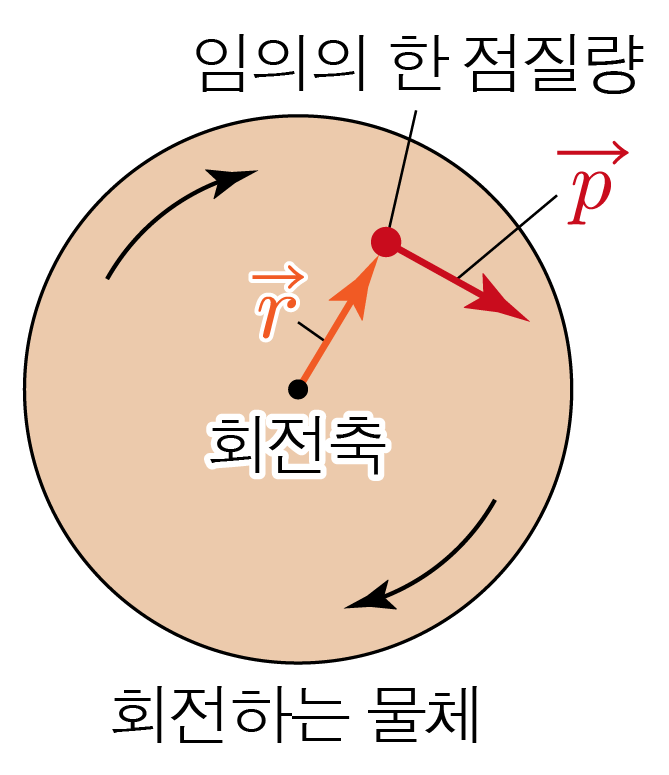
물체가 수많은 점으로 이루어져 있다고 가정할 때, 한 점의 질량이다.
단위 시간(1s) 동안 각속도의 변화이다.
기본 단위는 rad/s2이고, 기호로는 α로 나타낸다.
기준점(주로 회전축)으로부터 점질량까지의 벡터를 r이라 하고, 점질량의 선운동량을 p라 할 때, r×p인 물리량의 합이다.
기본 단위는 kg⋅m2/s=N⋅m⋅s이고, 기호로는 L로 나타낸다.
어느 강체의 관성 모멘트를 I, 각속도를 ω, 각가속도를 α라 할 때, 이 강체의 각운동량은 Iω이고, 강체에 작용하는 돌림힘의 합(알짜 돌림힘)은 Iα와 같다.
강체가 회전 운동만 하여 질량 중심의 위치가 일정하더라도,
점질량은 회전하여 운동을 하기 때문에 강체는 각운동량을 갖게 된다.
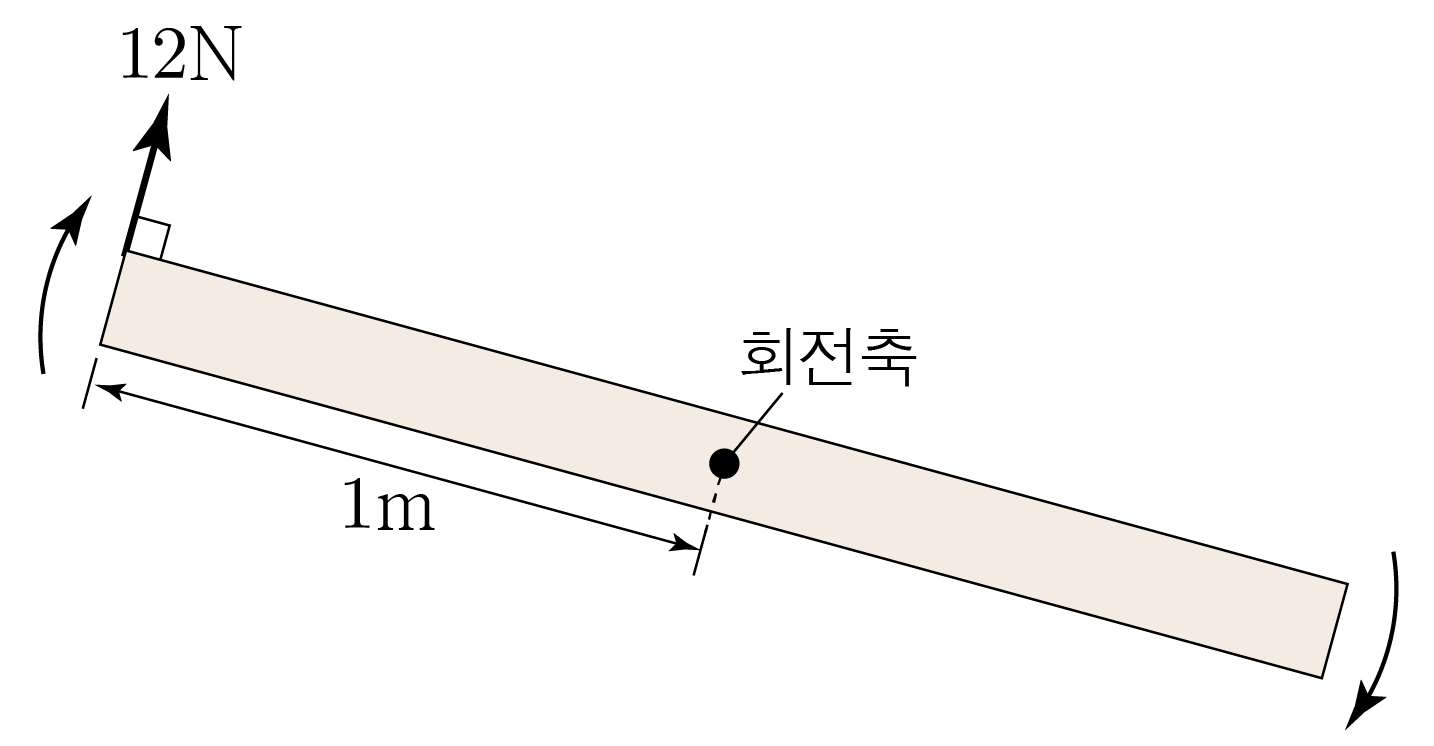
그림은 수평면 위에 놓여 있고, 길이가 2m인 균일한 막대에 수직 방향으로 크기가 12N인 힘을 작용하였더니 회전 운동을 하는 모습을 나타낸 것이다.
막대의 관성 모멘트는 2kg⋅m2이고, 각가속도의 크기는 α이다. α는? (단, 모든 마찰은 무시한다.)
회전축을 기준으로 막대에는 크기가 1m×12N=12N⋅m인 돌림힘이 작용한다.
강체의 관성 모멘트를 I라 할 때, 강체에 작용하는 돌림힘의 합(알짜 돌림힘)은 Iα와 같으므로
12N⋅m=2kg⋅m2×α,
12N⋅m=2αkg⋅m2,
12(kg⋅m/s2)⋅m=2αkg⋅m2,
12kg⋅m2/s2=2αkg⋅m2,
12s−2=2α,
α=6s−2=6rad/s2이다.
물체에 작용하는 알짜 돌림힘이 0일 때, 물체의 각운동량은 항상 일정하다.
피겨 스케이터가 빙판 위에서 회전할 때, 마찰력이 거의 작용하지 않아 피겨 스케이터에 작용하는 알짜 돌림힘은 0에 가깝다고 할 수 있다.
따라서 피겨 스케이터의 각운동량은 보존되므로 피겨 스케이터를 강체라 가정할 때, Iω는 항상 일정하다.
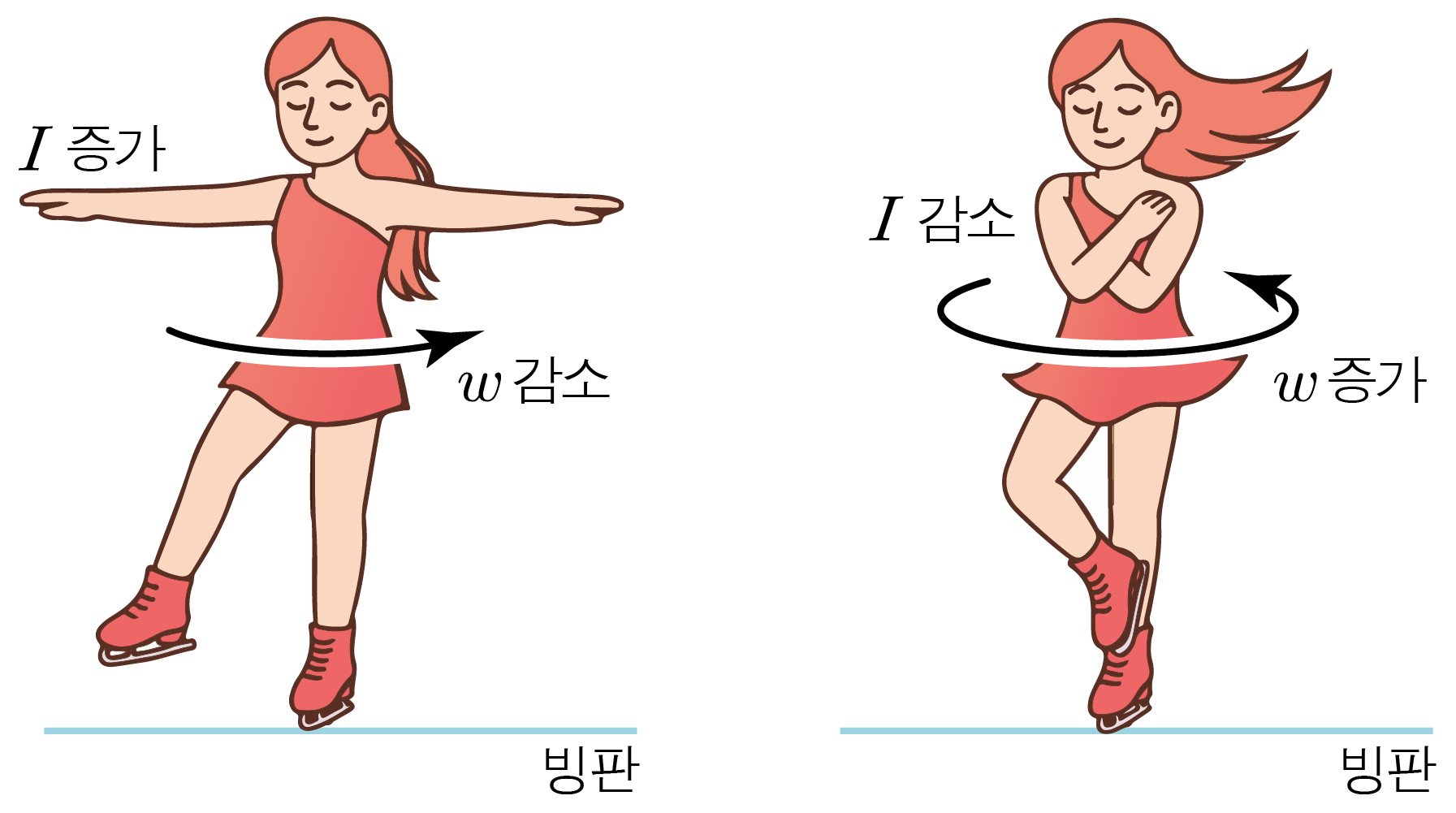
Iω는 항상 일정하게 유지되는데 피겨 스케이터가 두 팔을 밖으로 벌리고 회전하면,
질량이 회전축에 멀리 분포하게 되어 피겨 스케이터의 관성 모멘트 I가 커지고, 각속도 ω는 작아진다.
피겨 스케이터가 두 팔을 안으로 모으고 회전하면, 질량이 회전축에 가까이 분포하게 되어
피겨 스케이터의 관성 모멘트 I가 작아지고, 각속도 ω는 커진다.
정답: $5$
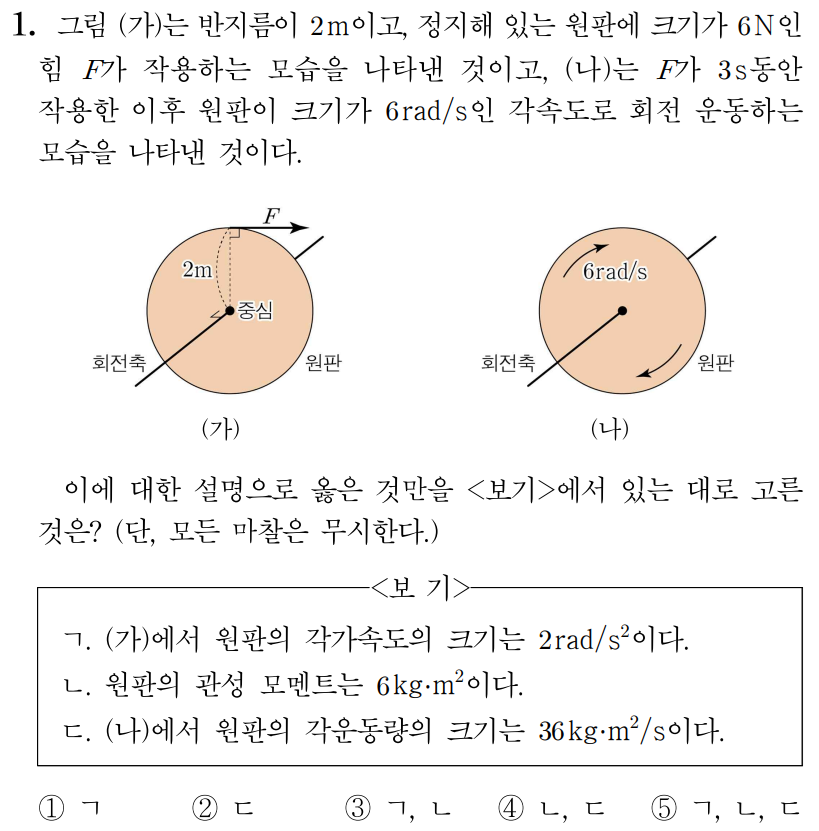
ㄱ. 각가속도는 단위 시간(1s) 동안 각속도의 변화이다.
원판은 3s 동안 각속도가 6rad/s만큼 변했으므로 원판의 각가속도의 크기를 α라 할 때,
α=3s6rad/s=2rad/s2이다. (O)
ㄴ. 회전축을 기준으로 원판에는 크기가 2m×6N=12N⋅m인 돌림힘이 작용한다.
강체의 관성 모멘트를 I라 할 때, 강체에 작용하는 돌림힘의 합(알짜 돌림힘)은 Iα와 같으므로
12N⋅m=I×2rad/s2,
12N⋅m=2Irad/s2,
12(kg⋅m/s2)⋅m=2Irad/s2,
12kg⋅m2/s2=2Irad/s2,
12kg⋅m2=2I,
I=6kg⋅m2이다. (O)
ㄷ. 강체의 각속도를 ω라 할 때, 각운동량은 Iω이므로 원판의 각운동량의 크기는
6kg⋅m2×6rad/s,
36kg⋅m2/s이다. (O)
따라서 정답은 5번이다.
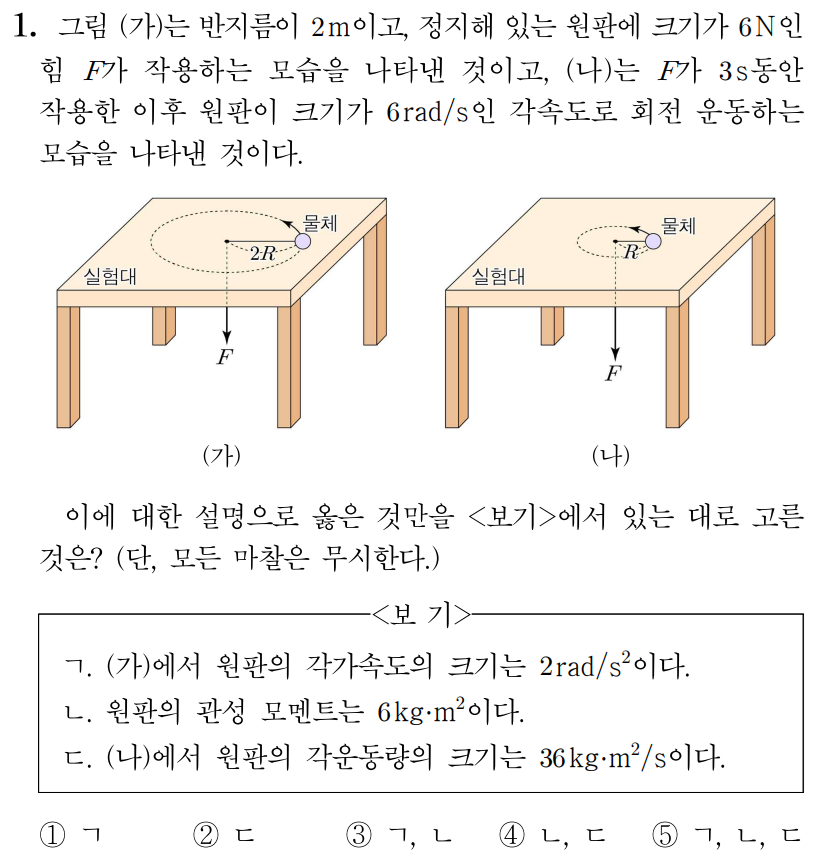
정답: $3$
ㄱ. 돌림힘은 기준점으로부터 힘이 작용한 지점까지의 벡터를 r이라 하고, r에 수직으로 작용하는 힘을 F라 할 때, r×F인 물리량이다.
물체에 작용하는 알짜힘은 물체를 원운동의 중심으로 당기는 장력과 같다.
따라서 회전축(실험대에 수직이고 실험대의 구멍을 통과하는 축)을 기준으로
물체까지의 벡터에 수직으로 작용하는 알짜힘은 F=0이므로 물체에 작용하는 알짜 돌림힘이 0이다.
물체에 작용하는 알짜 돌림힘이 0일 때, 각운동량 보존 법칙에 의해 물체의 각운동량은 항상 일정하므로
물체의 각운동량의 크기는 (가)와 (나)에서 서로 같다. (O)
ㄴ. 물체의 질량을 m이라 할 때, 물체의 관성 모멘트는 (가)와 (나)에서 각각 m(2R)2=4mR2, mR2이다.
물체의 각운동량의 크기는 (가)와 (나)에서 서로 같으므로 (가)와 (나)에서 물체의 각속도의 크기를 각각 ω(가), ω(나)라 할 때,
4mR2×ω(가)=mR2×ω(나),
4ω(가)=ω(나)이다.⋯①
그러므로 각속도의 크기는 (나)에서가 (가)에서의 4배이다. (O)
ㄷ. ①에서 4ω(가)=ω(나)이므로 ω(가), ω(나)를 각각 ω, 4ω라 하자.
물체의 회전 반지름을 r이라 할 때, 물체의 속력 v=rω이므로 물체의 속력은
(가)에서 2R×ω=2Rω, (나)에서 R×4ω=4Rω이다.
그러므로 물체의 속력은 (나)에서가 (가)에서의 2배이다. (X)
따라서 정답은 3번이다.