어느 관찰자를 기준으로 한 물체의 속도이다.
버스 안에서 밖을 볼 때 본인은 정지해 있는데 나무가 움직이는 것처럼 보이듯이, 관찰자는 자신이 정지해 있다고 생각하여 관찰자의 속도에 따라 상대 속도가 달라진다.
관찰자 A A B B v A v A v B v B A A B B v B − v A v B − v A A A B B v A B v A B
A A B B v A B = v B − v A v A B = v B − v A B B A A v B A = v A − v B v B A = v A − v B
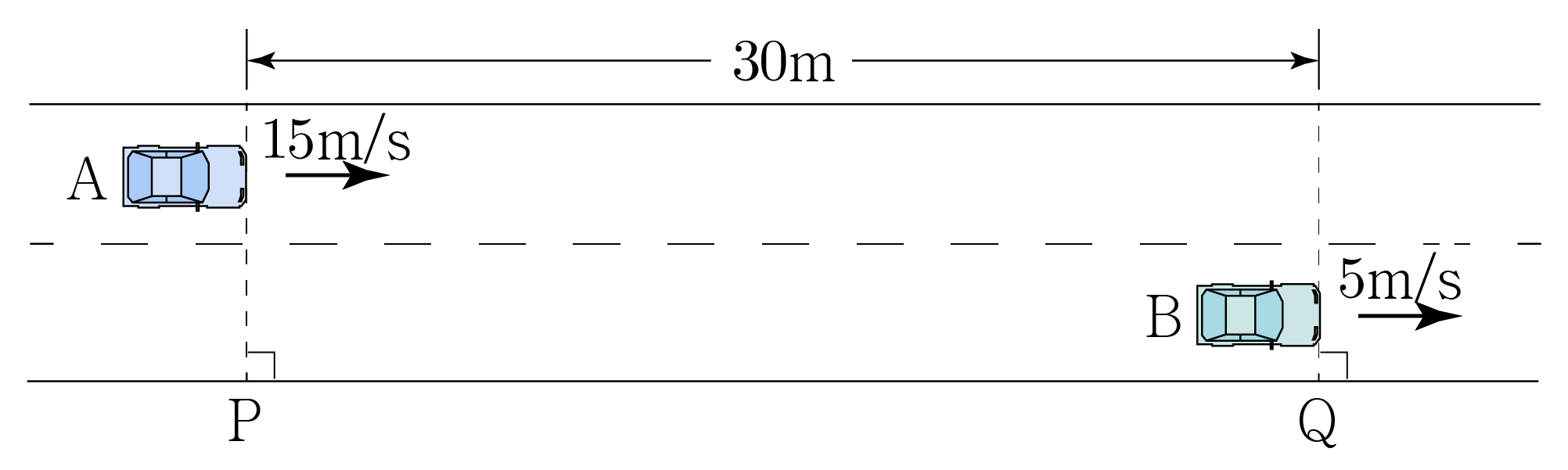
그림과 같이 직선 도로에서 시간 t = 0 t = 0 A A B B 15 m / s 1 5 m / s 5 m / s 5 m / s P P Q Q P P Q Q 30 m 3 0 m A A B B t = x t = x x x A A B B
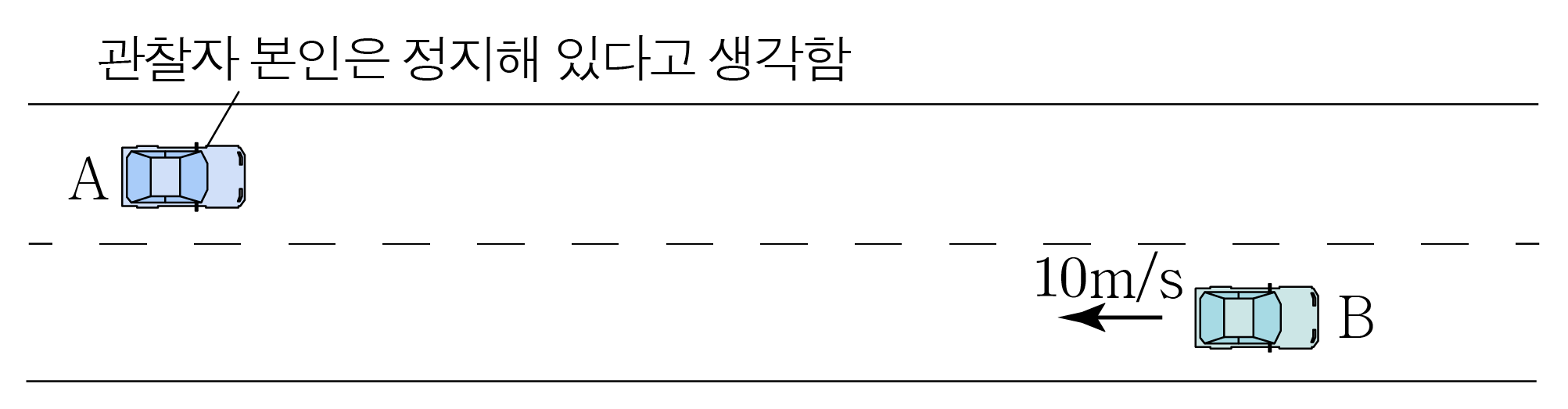
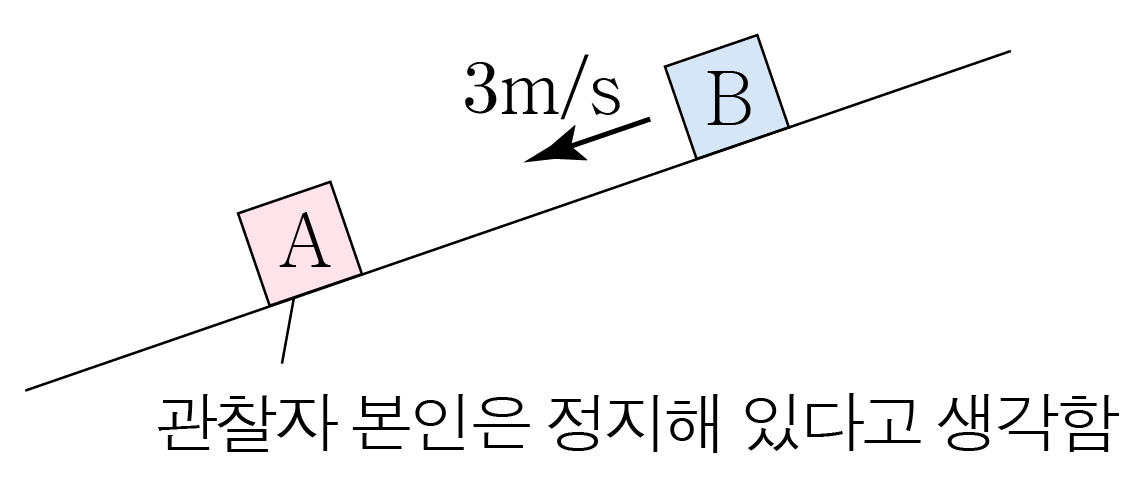
A A B B v B − v A v B − v A ( + ) ( + ) v A B = 5 m / s − 15 m / s = − 10 m / s v A B = 5 m / s − 1 5 m / s = − 1 0 m / s
그러므로 아래 그림과 같이 A A B B 10 m / s 1 0 m / s A A
따라서x = 30 m 10 m / s , x = 1 0 m / s 3 0 m , x = 3 m 1 m / s , x = 1 m / s 3 m , x = 3 1 / s , x = 1 / s 3 , x = 3 × s ( 1 / s ) × s , x = ( 1 / s ) × s 3 × s , x = 3 s x = 3 s
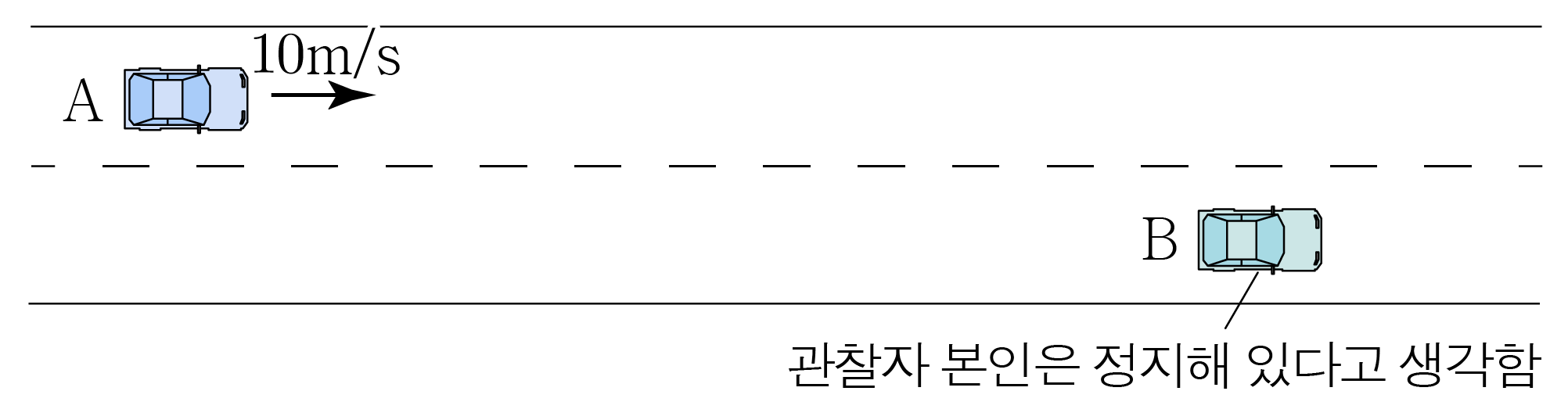
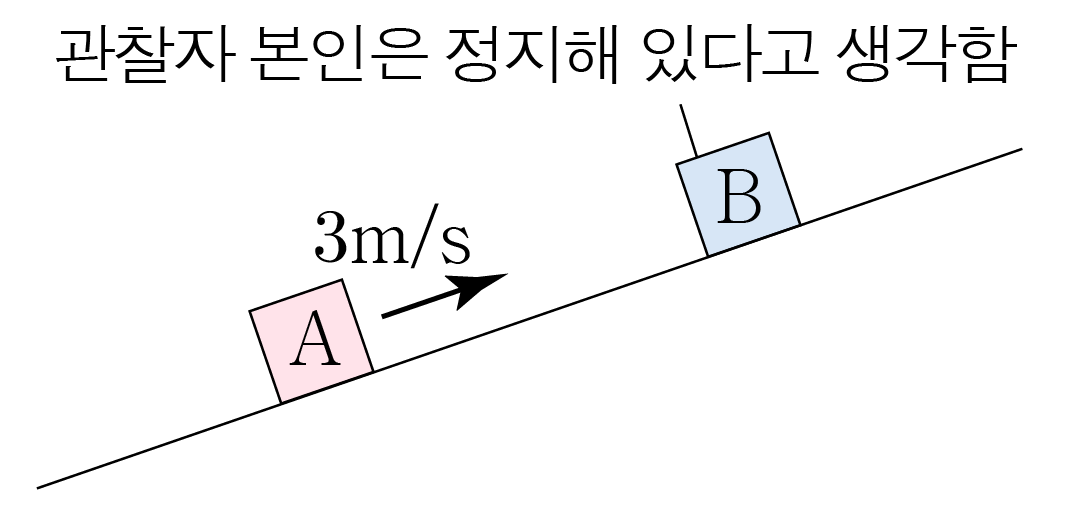
B B A A v A − v B v A − v B ( + ) ( + ) v B A = 15 m / s − 5 m / s = 10 m / s v B A = 1 5 m / s − 5 m / s = 1 0 m / s
그러므로 아래 그림과 같이 B B A A 10 m / s 1 0 m / s B B
따라서x = 30 m 10 m / s , x = 1 0 m / s 3 0 m , x = 3 m 1 m / s , x = 1 m / s 3 m , x = 3 1 / s , x = 1 / s 3 , x = 3 × s ( 1 / s ) × s , x = ( 1 / s ) × s 3 × s , x = 3 s x = 3 s
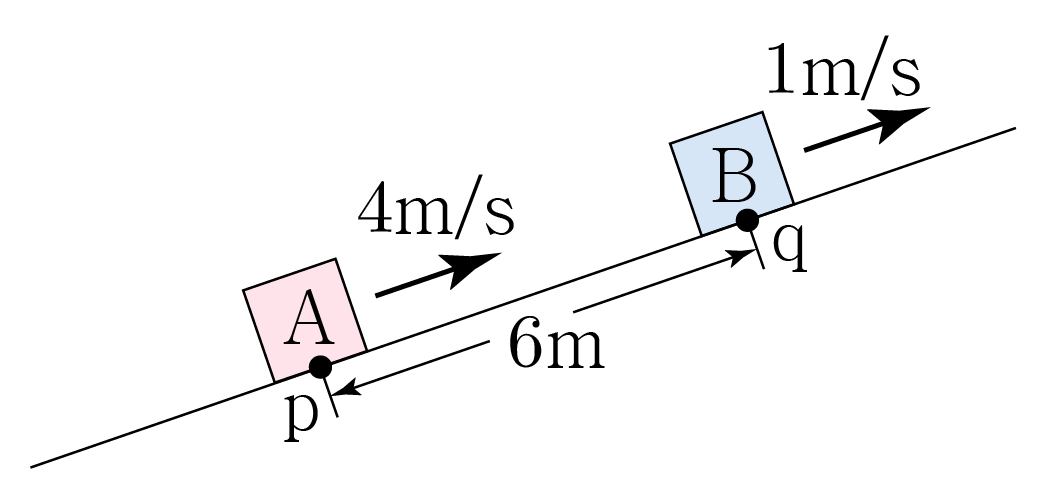
그림과 같이 빗면에서 시간 t = 0 t = 0 A A B B 4 m / s 4 m / s 1 m / s 1 m / s p p q q p p q q 6 m 6 m A A B B t = x t = x x x A A B B
빗면을 올라가는 방향을 양( + ) ( + ) A A B B a a t = x t = x A A B B ( 4 m / s − a x ) , ( 4 m / s − a x ) , ( 1 m / s − a x ) ( 1 m / s − a x )
다음으로 t = x t = x A A B B
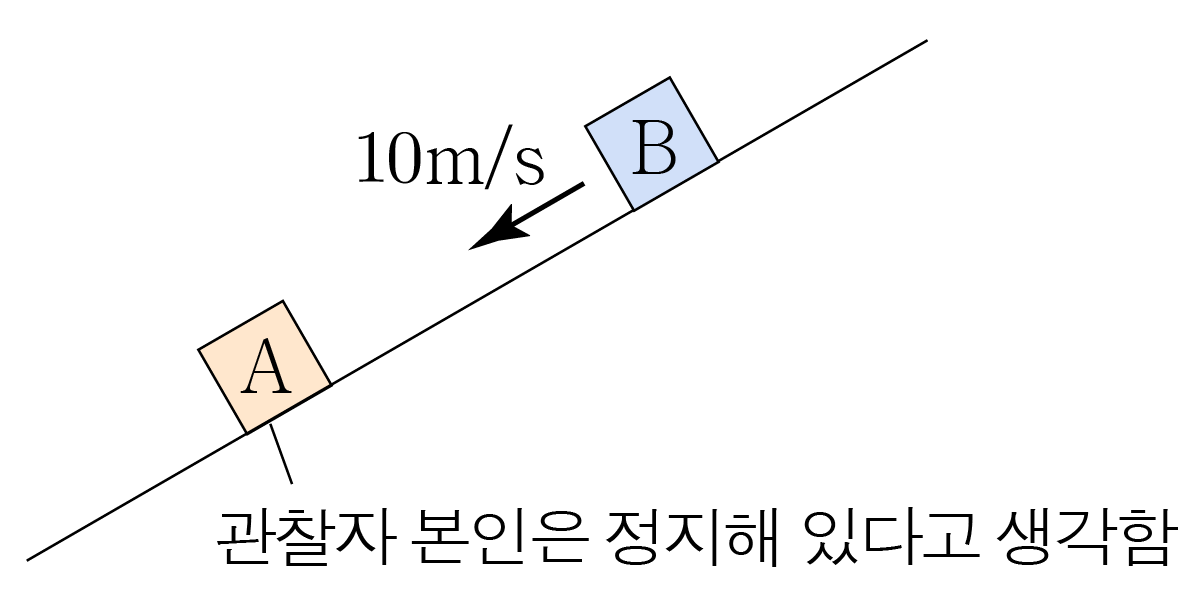
A A B B v B − v A v B − v A v A B = 1 m / s − a x − ( 4 m / s − a x ) , v A B = 1 m / s − a x − ( 4 m / s − a x ) , v A B = 1 m / s − a x − 4 m / s + a x , v A B = 1 m / s − a x − 4 m / s + a x , v A B = − 3 m / s v A B = − 3 m / s
그러므로 아래 그림과 같이 A A B B 3 m / s 3 m / s
따라서x = 6 m 3 m / s , x = 3 m / s 6 m , x = 2 m 1 m / s , x = 1 m / s 2 m , x = 2 1 / s , x = 1 / s 2 , x = 2 × s ( 1 / s ) × s , x = ( 1 / s ) × s 2 × s , x = 2 s x = 2 s
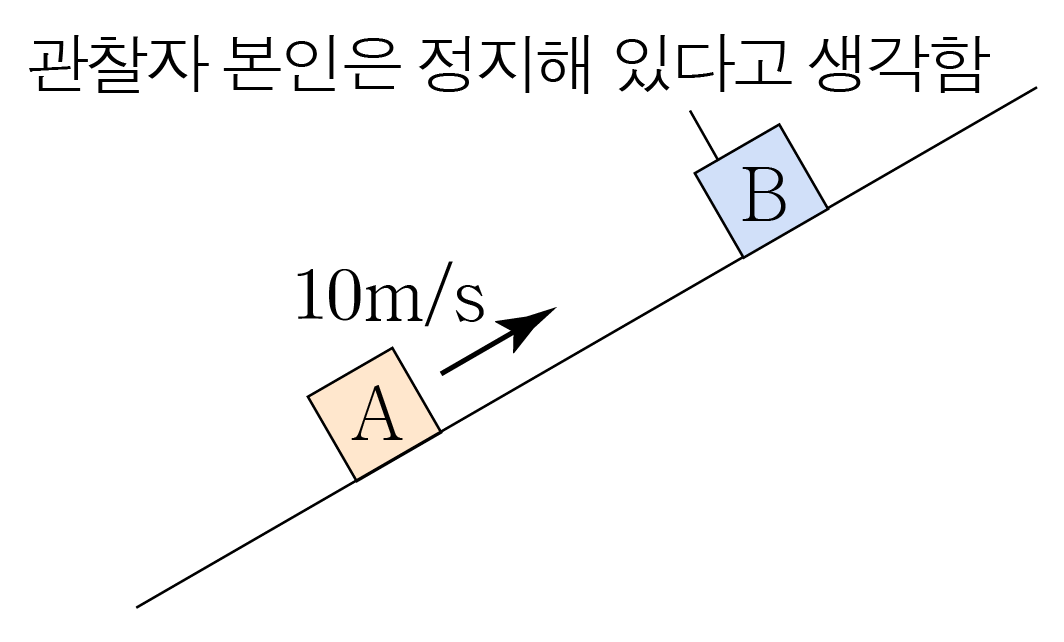
B B A A v A − v B v A − v B v B A = 4 m / s − a x − ( 1 m / s − a x ) , v B A = 4 m / s − a x − ( 1 m / s − a x ) , v B A = 4 m / s − a x − 1 m / s + a x , v B A = 4 m / s − a x − 1 m / s + a x , v B A = 3 m / s v B A = 3 m / s
그러므로 아래 그림과 같이 B B A A 3 m / s 3 m / s
따라서x = 6 m 3 m / s , x = 3 m / s 6 m , x = 2 m 1 m / s , x = 1 m / s 2 m , x = 2 1 / s , x = 1 / s 2 , x = 2 × s ( 1 / s ) × s , x = ( 1 / s ) × s 2 × s , x = 2 s x = 2 s
1번 문항 정답 및 해설 보기
정답: $5$
ㄱ. A A A A 0 0
ㄴ. A A B B A A B B A A B B A A B B A A
A A B B t = 5 s t = 5 s A A B B 45 m 5 s = 9 m / s 5 s 4 5 m = 9 m / s
ㄷ. A A B B v A v A v B v B A A B B v B − v A v B − v A ( + ) ( + ) v B − v A = − 9 m / s , v B − v A = − 9 m / s , − 6 m / s − V = − 9 m / s , − 6 m / s − V = − 9 m / s , − 6 m / s + 9 m / s = V , − 6 m / s + 9 m / s = V , V = 3 m / s V = 3 m / s
따라서 정답은 5 5
2번 문항 정답 및 해설 보기
정답: $3$
중력 가속도의 크기를 g g θ θ g sin θ g sin θ A A B B g sin θ = 10 m / s 2 × sin 3 0 ∘ = 10 m / s 2 × 1 2 = 5 m / s 2 g sin θ = 1 0 m / s 2 × sin 3 0 ∘ = 1 0 m / s 2 × 2 1 = 5 m / s 2
빗면을 올라가는 방향을 양( + ) ( + ) A A B B p p q q t t A A B B ( 10 m / s − 5 t m / s 2 ) ( 1 0 m / s − 5 t m / s 2 ) − 5 t m / s 2 − 5 t m / s 2
다음으로 A A B B
A A B B v B − v A v B − v A v A B = − 5 t m / s 2 − ( 10 m / s − 5 t m / s 2 ) , v A B = − 5 t m / s 2 − ( 1 0 m / s − 5 t m / s 2 ) , v A B = − 5 t m / s 2 − 10 m / s + 5 t m / s 2 , v A B = − 5 t m / s 2 − 1 0 m / s + 5 t m / s 2 , v A B = − 10 m / s v A B = − 1 0 m / s
그러므로 아래 그림과 같이 A A B B 10 m / s 1 0 m / s
A A B B 1 s 1 s 10 m 1 0 m A A B B p p q q x x x = 60 m 10 m / s , x = 1 0 m / s 6 0 m , x = 6 m 1 m / s , x = 1 m / s 6 m , x = 6 1 / s , x = 1 / s 6 , x = 6 × s ( 1 / s ) × s , x = ( 1 / s ) × s 6 × s , x = 6 s x = 6 s
이때 A A − 5 m / s 2 − 5 m / s 2 A A p p 6 s 6 s B B A A 10 m / s − 5 m / s 2 × 6 s = 10 m / s − 30 m / s = − 20 m / s 1 0 m / s − 5 m / s 2 × 6 s = 1 0 m / s − 3 0 m / s = − 2 0 m / s
속력은 속도의 크기에 해당하므로 V = ∣ − 20 m / s ∣ = 20 m / s V = ∣ − 2 0 m / s ∣ = 2 0 m / s
B B A A v A − v B v A − v B v B A = 10 m / s − 5 t m / s 2 − ( − 5 t m / s 2 ) , v B A = 1 0 m / s − 5 t m / s 2 − ( − 5 t m / s 2 ) , v B A = 10 m / s − 5 t m / s 2 + 5 t m / s 2 , v B A = 1 0 m / s − 5 t m / s 2 + 5 t m / s 2 , v B A = 10 m / s v B A = 1 0 m / s
그러므로 아래 그림과 같이 B B A A 10 m / s 1 0 m / s
A A B B 1 s 1 s 10 m 1 0 m A A B B p p q q x x x = 60 m 10 m / s , x = 1 0 m / s 6 0 m , x = 6 m 1 m / s , x = 1 m / s 6 m , x = 6 1 / s , x = 1 / s 6 , x = 6 × s ( 1 / s ) × s , x = ( 1 / s ) × s 6 × s , x = 6 s x = 6 s
이때 A A − 5 m / s 2 − 5 m / s 2 A A p p 6 s 6 s B B A A 10 m / s − 5 m / s 2 × 6 s = 10 m / s − 30 m / s = − 20 m / s 1 0 m / s − 5 m / s 2 × 6 s = 1 0 m / s − 3 0 m / s = − 2 0 m / s
속력은 속도의 크기에 해당하므로 V = ∣ − 20 m / s ∣ = 20 m / s V = ∣ − 2 0 m / s ∣ = 2 0 m / s
따라서 정답은 3 3