벡터 a와 b의 내적은 a⋅b로 나타내고,
a와 b가 이루는 각이 θ일 때, a⋅b의 값은 ∣a∣∣b∣cosθ인 스칼라이다.
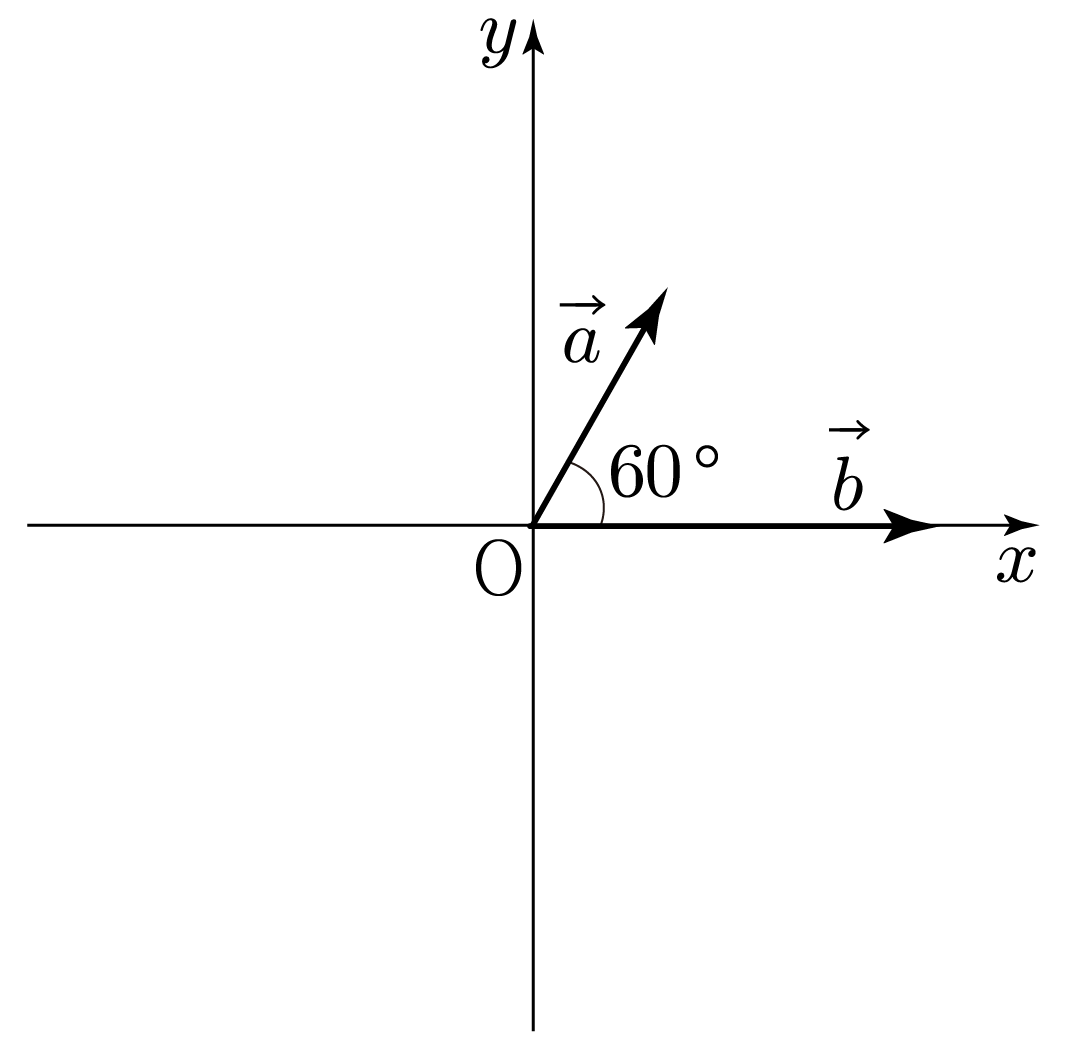
그림과 같이 벡터 a와 b가 있다.
a와 b의 크기가 각각 2, 3일 때, a⋅b를 구해보자.
∣a∣=2,∣b∣=3이고 a와 b가 이루는 각이 60∘이므로
a⋅b=∣a∣∣b∣cos60∘=2×3×21=3이다.
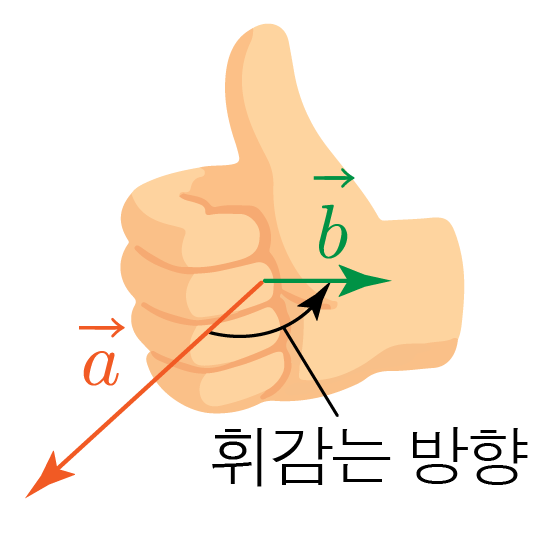
벡터 a와 b의 외적은 a×b로 나타내고,
a와 b가 이루는 각이 θ일 때, a×b의 값은 크기가 ∣a∣∣b∣sinθ이고 방향은 a와 b에 수직인 벡터이다.
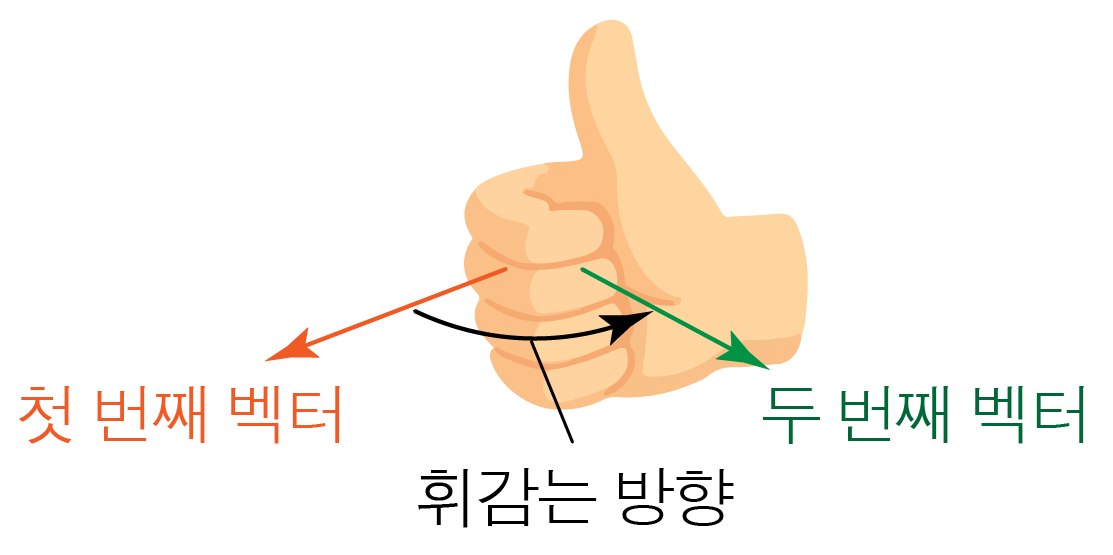
1. 오른손으로 엄지척 모양을 만든다.
2. 첫 번째 벡터에서 두 번째 벡터 방향으로 엄지를 제외한 손가락을 휘감는다.
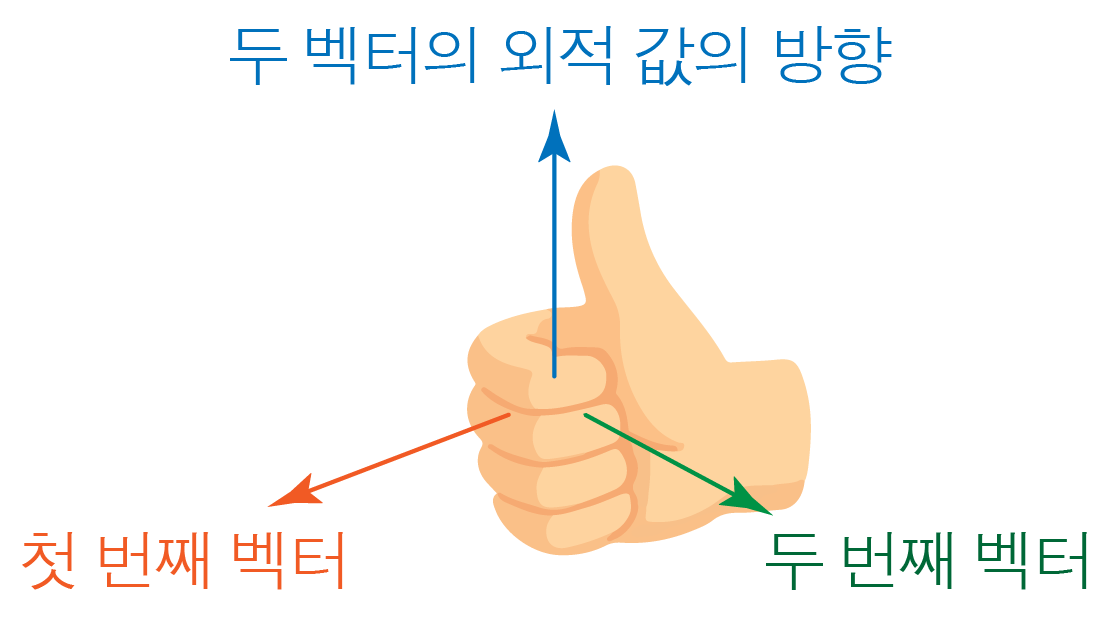
3. 엄지가 향하는 방향이 두 벡터의 외적 값의 방향이다.
a×b에서 첫 번째 벡터는 a, 두 번째 벡터는 b이고,
b×a에서 첫 번째 벡터는 b, 두 번째 벡터는 a이다.
벡터의 순서에 따라 외적 값의 방향이 달라짐에 주의한다.
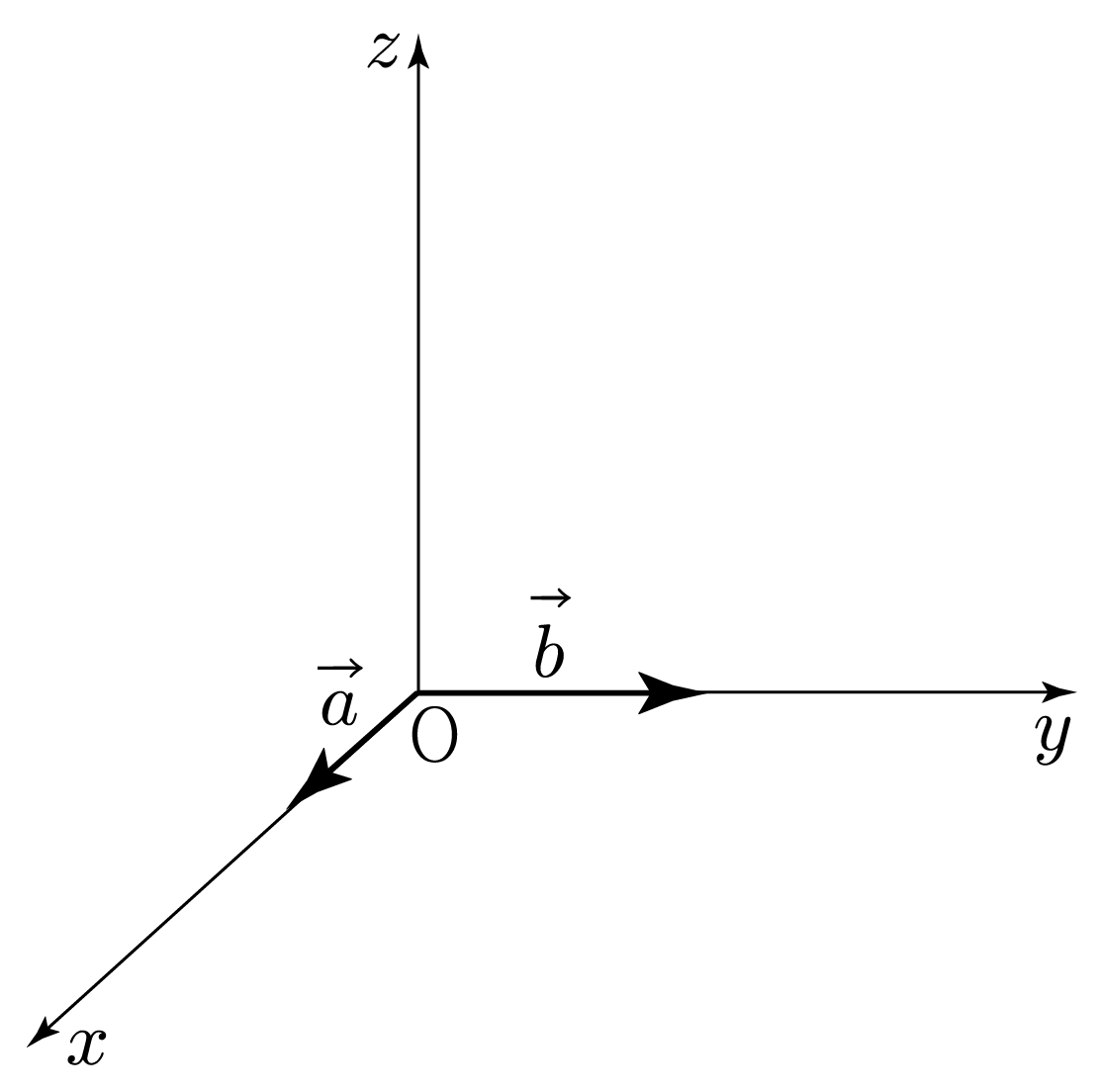
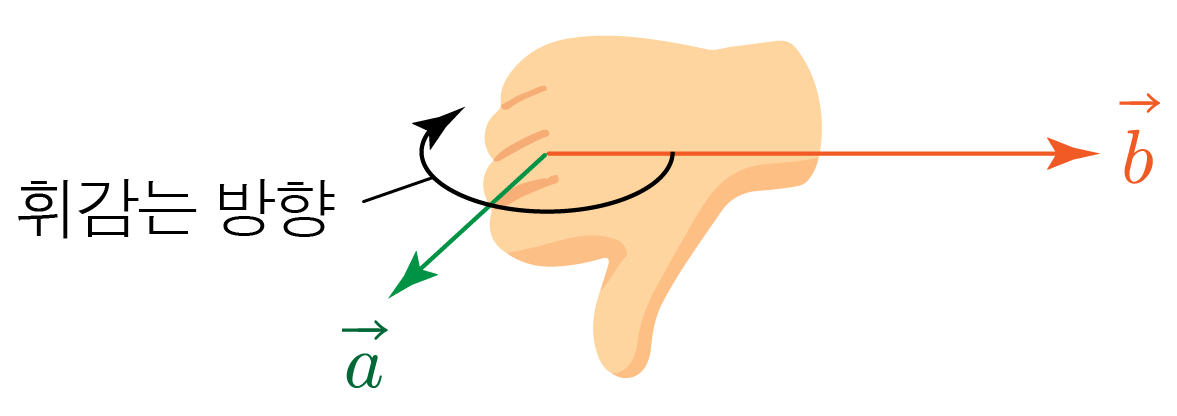
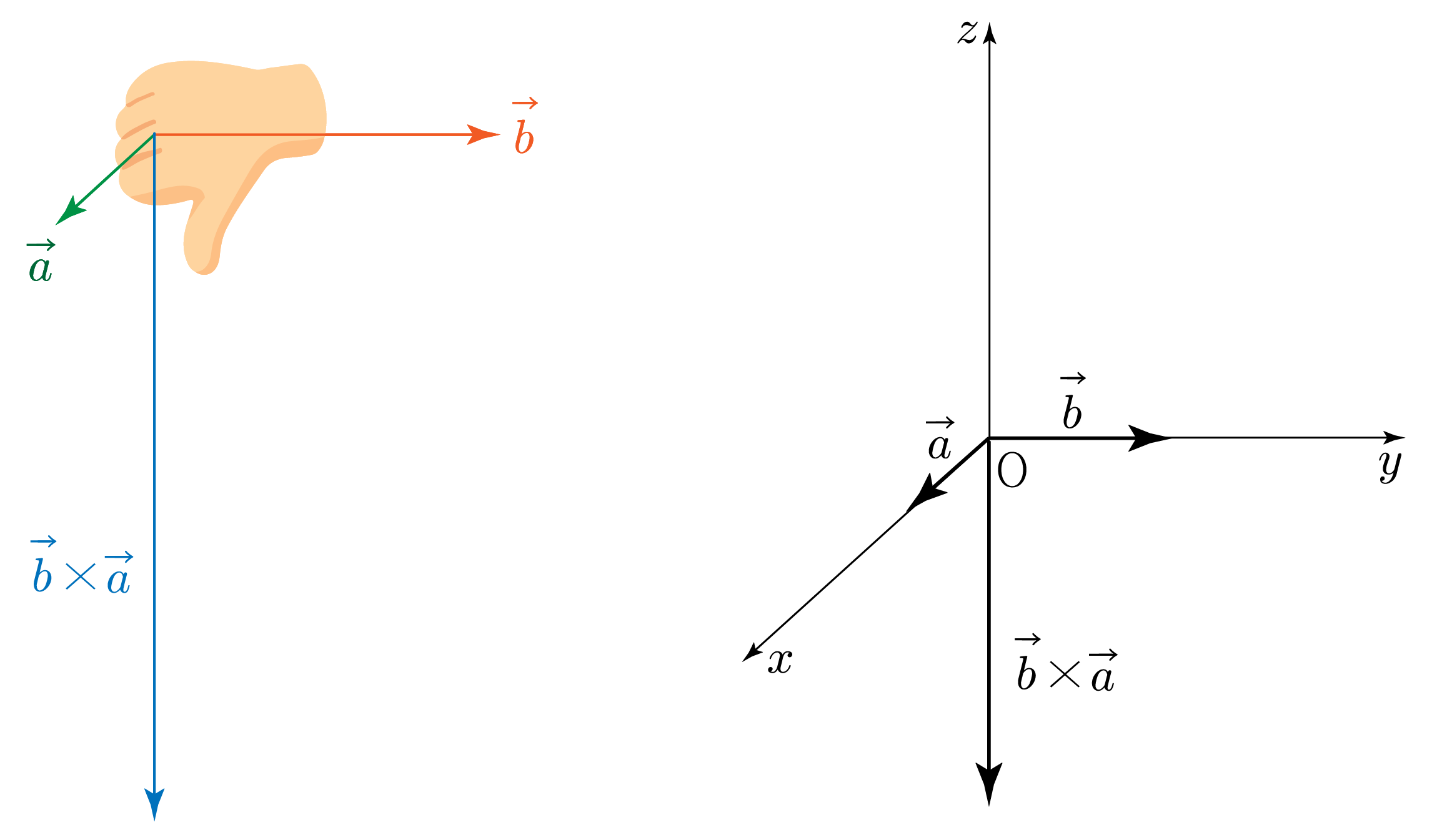
그림과 같이 좌표 공간에 벡터 a와 b가 있다. a와 b는 각각 x축과 y축에 나란하다.
a와 b의 크기가 각각 2, 3일 때, b×a를 구해보자.
크기 구하기:
∣a∣=2,∣b∣=3이고 a와 b가 이루는 각이 90∘이므로
∣b×a∣=∣b∣∣a∣sin90∘=3×2×1=6이다.
방향 구하기:
1. 오른손으로 엄지척 모양을 만든다.
2. b(첫 번째 벡터)에서 a(두 번째 벡터) 방향으로 엄지를 제외한 손가락을 휘감는다.
3. −z축 방향(엄지가 향하는 방향)이 두 벡터의 외적 값의 방향이다.
따라서 b×a는 −z축 방향이고, 크기가 6인 벡터이다.
정답: $2$
∣a∣=4,∣b∣=3이고 a와 b가 이루는 각이 30∘이므로
a⋅b=∣a∣∣b∣cos30∘=4×3×23=63이다.
따라서 정답은 2번이다.

정답: $1$
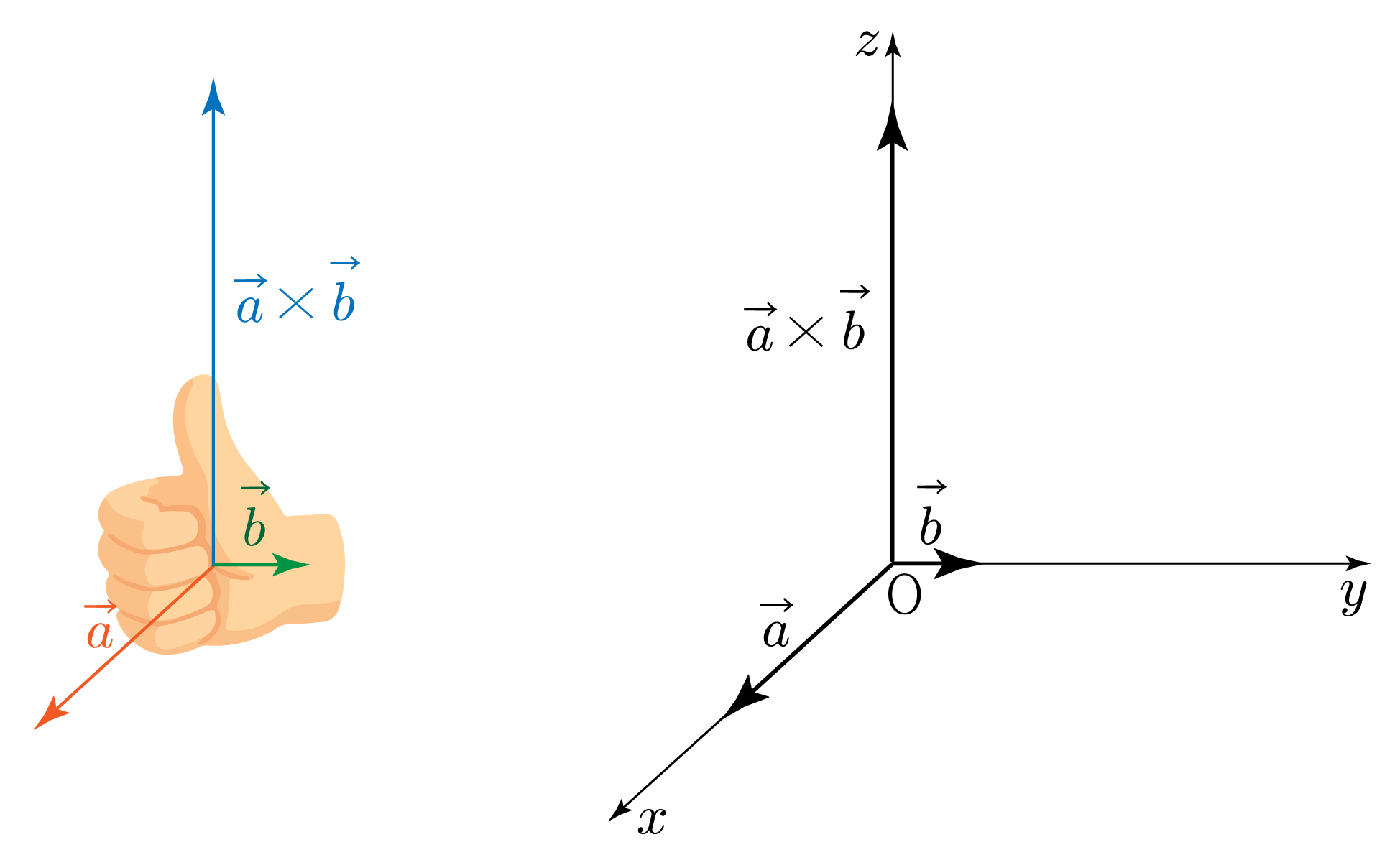
크기 구하기:
∣a∣=5,∣b∣=2이고 a와 b가 이루는 각이 90∘이므로
∣a×b∣=∣a∣∣b∣sin90∘=5×2×1=10이다.
방향 구하기:
1. 오른손으로 엄지척 모양을 만든다.
2. a(첫 번째 벡터)에서 b(두 번째 벡터) 방향으로 엄지를 제외한 손가락을 휘감는다.
3. z축 방향(엄지가 향하는 방향)이 두 벡터의 외적 값의 방향이다.
그러므로 a×b는 +z축 방향이고, 크기가 10인 벡터이다.
따라서 정답은 1번이다.