해당 지식
하위 지식
상위 지식
$-$
물체가 평형 상태의 조건을 만족하지 못해 가속도를 가지는 것이다.
1. 1 . 2. 2 . 1 1
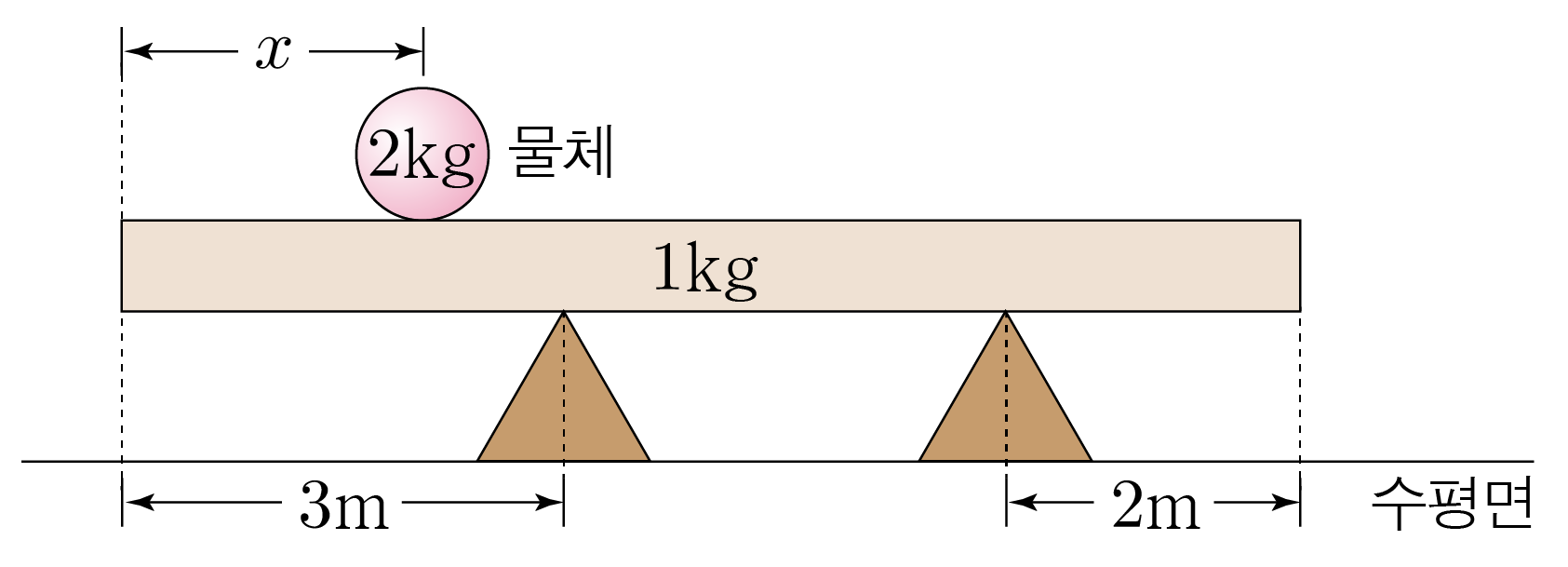
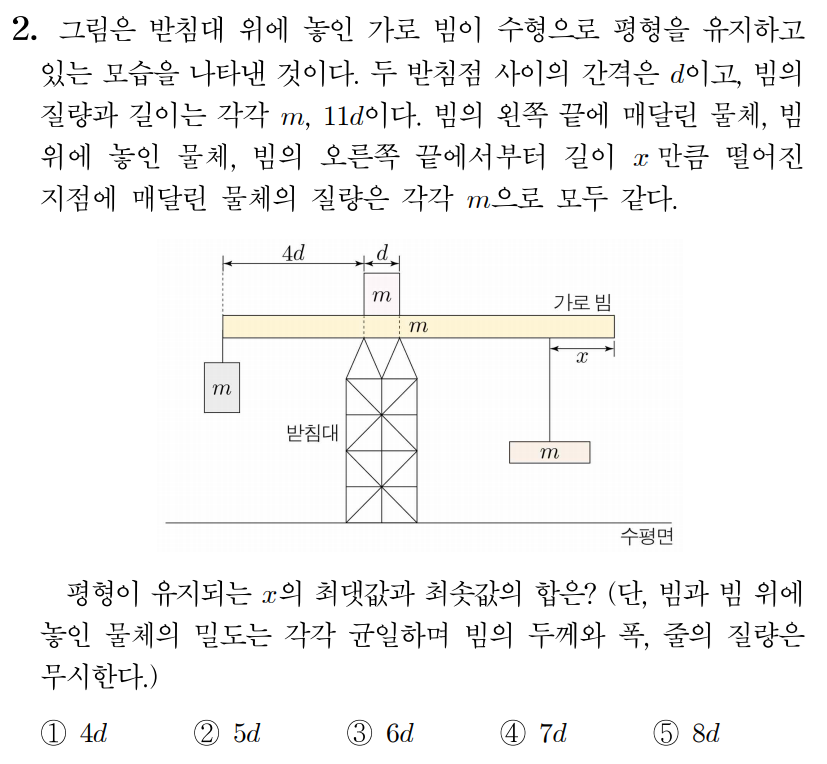
그림과 같이 두 받침대 위에 놓인 막대가 수평으로 평형을 유지하고 있고, 막대 위에 물체가 놓여 있다. 막대, 물체의 질량은 각각 1 k g 1 k g 2 k g 2 k g 8 m 8 m x x x x 10 m / s 2 1 0 m / s 2
물체가 막대를 누르는 힘의 크기와 막대의 무게를 구하면 아래와 같다.
물체가 막대를 누르는 힘의 크기:2 k g × 10 m / s 2 = 20 k g ⋅ m / s 2 = 20 2 k g × 1 0 m / s 2 = 2 0 k g ⋅ m / s 2 = 2 0
막대의 무게:1 k g × 10 m / s 2 = 10 k g ⋅ m / s 2 = 10 1 k g × 1 0 m / s 2 = 1 0 k g ⋅ m / s 2 = 1 0
막대에 작용하는 알짜힘이 0 0 20 N + 10 N = 30 N 2 0 N + 1 0 N = 3 0 N
1. 1 . x x
평형이 붕괴된 직후 막대의 회전 방향을 통해 붕괴 직전 막대에 작용하는 힘을 구해보자.
물체와 막대를 하나의 계로 볼 때, 계의 질량 중심이 왼쪽 받침대보다 왼쪽으로 치우치면0 0
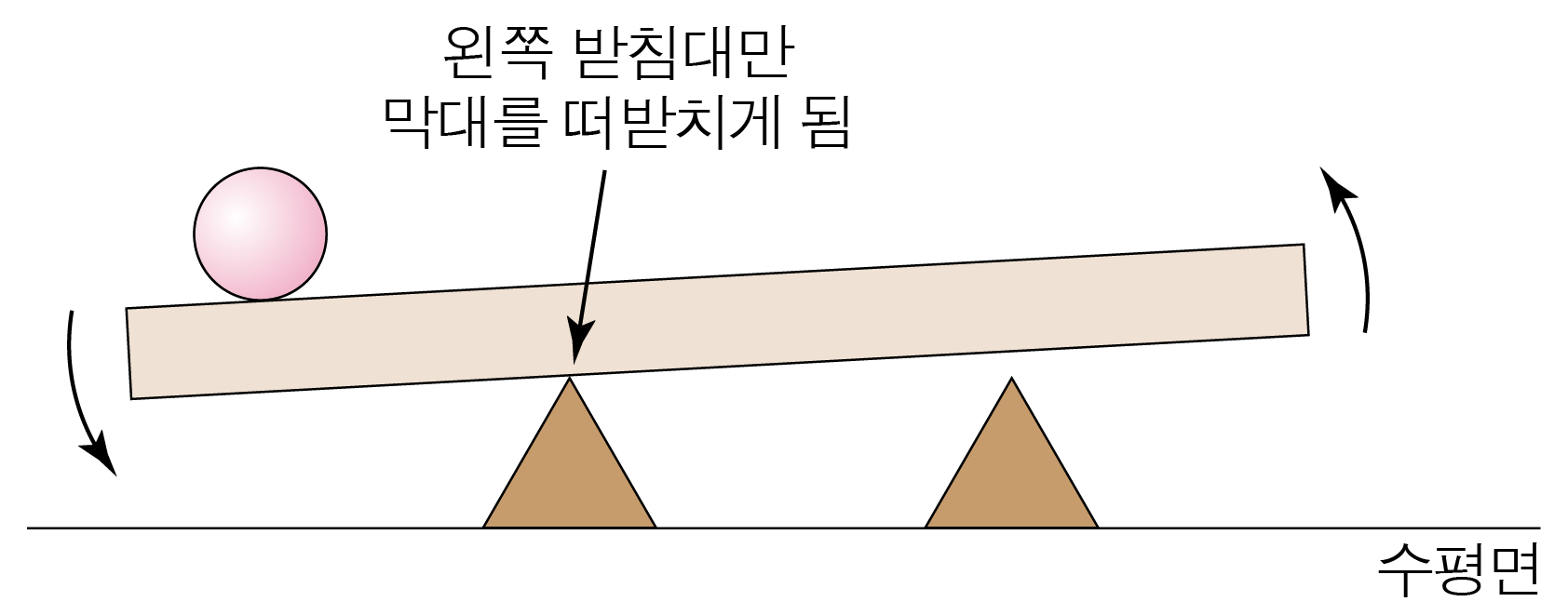
이때 아래 그림과 같이 왼쪽 받침대만 막대를 떠받치게 되므로, x x 0 0
그러므로 x x x min x m i n
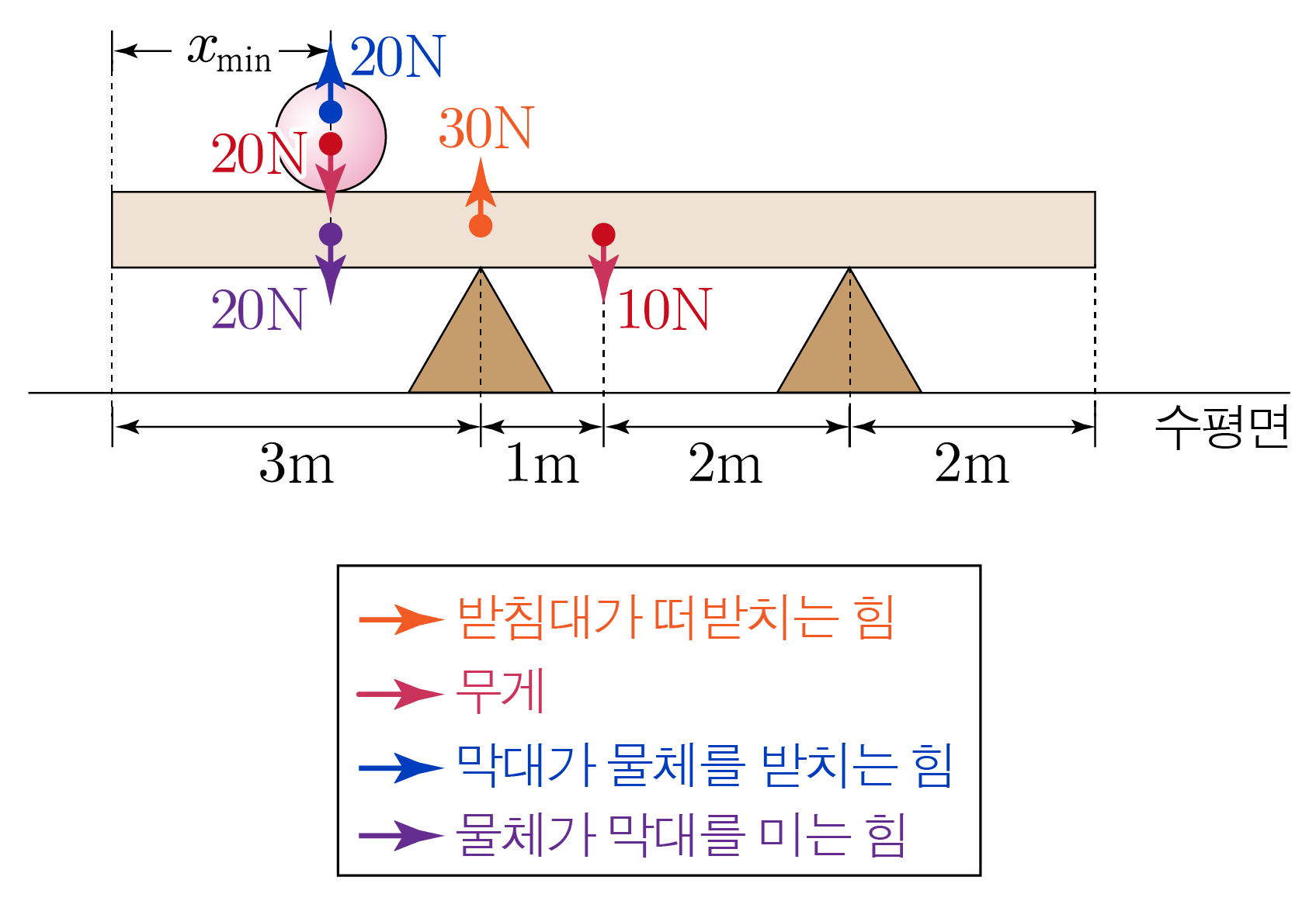
막대의 가장 왼쪽 지점을 기준점으로 할 때, 막대에 작용하는 각 힘에 의한 돌림힘을 구하면 아래와 같다.
물체가 막대를 누르는 힘에 의한 돌림힘:− x min × 20 N = − 20 x min − x m i n × 2 0 N = − 2 0 x m i n
막대의 무게에 의한 돌림힘:− 4 m × 10 N = − 40 − 4 m × 1 0 N = − 4 0
받침대가 물체를 떠받치는 힘에 의한 돌림힘:3 m × 30 N = 90 3 m × 3 0 N = 9 0
막대에 작용하는 돌림힘의 합이 0 0 − 20 x min N − 40 N ⋅ m + 90 N ⋅ m = 0 − 2 0 x m i n N − 4 0 N ⋅ m + 9 0 N ⋅ m = 0 − 20 x min N + 50 N ⋅ m = 0 , − 2 0 x m i n N + 5 0 N ⋅ m = 0 , 50 N ⋅ m = 20 x min N , 5 0 N ⋅ m = 2 0 x m i n N , 5 m = 2 x min , 5 m = 2 x m i n , x min = 5 2 m x m i n = 2 5 m
질량 중심으로 x min x m i n
x x
막대, 물체를 각각 1 , 2 1 , 2 m 1 = 1 k g , m 1 = 1 k g , m 2 = 2 k g m 2 = 2 k g
따라서 ∑ i = 1 n m i = ∑ i = 1 2 m i = m 1 + m 2 = 1 k g + 2 k g = 3 k g i = 1 ∑ n m i = i = 1 ∑ 2 m i = m 1 + m 2 = 1 k g + 2 k g = 3 k g
아래쪽 막대의 가장 왼쪽 지점을 기준점이라 하면 r 1 = 4 m , r 1 = 4 m , r 2 = x min r 2 = x m i n
그러므로 ∑ i = 1 n m i r i = ∑ i = 1 2 m i r i , i = 1 ∑ n m i r i = i = 1 ∑ 2 m i r i , ∑ i = 1 n m i r i = m 1 r 1 + m 2 r 2 , i = 1 ∑ n m i r i = m 1 r 1 + m 2 r 2 , ∑ i = 1 n m i r i = ( 1 k g × 4 m ) + ( 2 k g × x min ) , i = 1 ∑ n m i r i = ( 1 k g × 4 m ) + ( 2 k g × x m i n ) , ∑ i = 1 n m i r i = 4 k g ⋅ m + 2 x min k g i = 1 ∑ n m i r i = 4 k g ⋅ m + 2 x m i n k g
질량 중심의 위치는 ∑ i = 1 n m i r i ∑ i = 1 n m i = ∑ i = 1 2 m i r i ∑ i = 1 2 m i = 4 k g ⋅ m + 2 x min k g 3 k g = 3 m i = 1 ∑ n m i i = 1 ∑ n m i r i = i = 1 ∑ 2 m i i = 1 ∑ 2 m i r i = 3 k g 4 k g ⋅ m + 2 x m i n k g = 3 m 4 k g ⋅ m + 2 x min k g 3 k g = 3 m , 3 k g 4 k g ⋅ m + 2 x m i n k g = 3 m , 4 k g ⋅ m + 2 x min k g = 9 k g ⋅ m , 4 k g ⋅ m + 2 x m i n k g = 9 k g ⋅ m , 4 m + 2 x min = 9 m , 4 m + 2 x m i n = 9 m , 2 x min = 5 m , 2 x m i n = 5 m , x min = 5 2 m x m i n = 2 5 m
2. 2 . x x
평형이 붕괴된 직후 막대의 회전 방향을 통해 붕괴 직전 막대에 작용하는 힘을 구해보자.
계의 질량 중심이 오른쪽 받침대보다 오른쪽으로 치우치면0 0
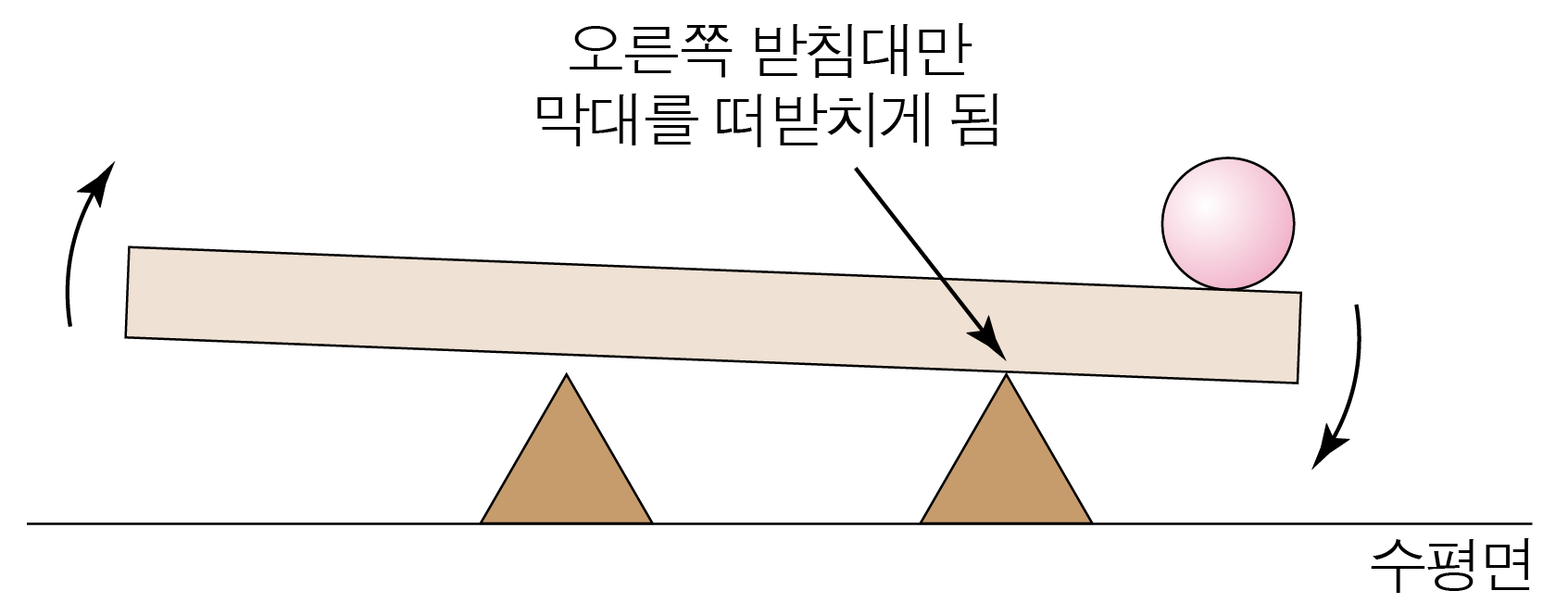
이때 아래 그림과 같이 오른쪽 받침대만 막대를 떠받치게 되므로,x x 0 0
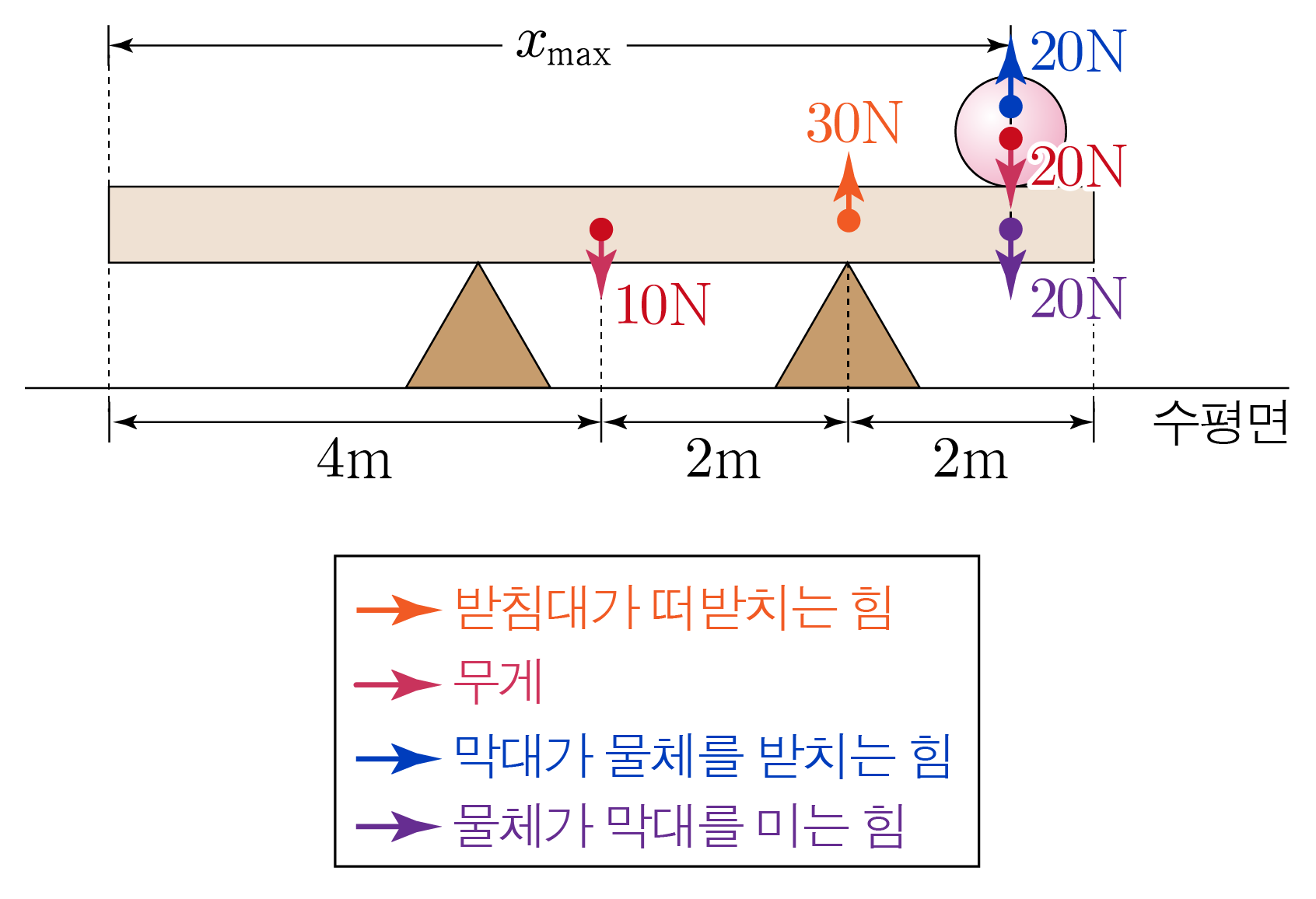
그러므로 x x x max x m a x
막대의 가장 왼쪽 지점을 기준점으로 할 때, 막대에 작용하는 각 힘에 의한 돌림힘을 구하면 아래와 같다.
물체가 막대를 누르는 힘에 의한 돌림힘:− x max × 20 N = − 20 x max − x m a x × 2 0 N = − 2 0 x m a x
막대의 무게에 의한 돌림힘:− 4 m × 10 N = − 40 − 4 m × 1 0 N = − 4 0
받침대가 물체를 떠받치는 힘에 의한 돌림힘:6 m × 30 N = 180 6 m × 3 0 N = 1 8 0
막대에 작용하는 돌림힘의 합이 0 0 − 20 x max N − 40 N ⋅ m + 180 N ⋅ m = 0 , − 2 0 x m a x N − 4 0 N ⋅ m + 1 8 0 N ⋅ m = 0 , − 20 x max N + 140 N ⋅ m = 0 , − 2 0 x m a x N + 1 4 0 N ⋅ m = 0 , 140 N ⋅ m = 20 x max N , 1 4 0 N ⋅ m = 2 0 x m a x N , x max = 7 m x m a x = 7 m
질량 중심으로 x max x m a x
x x
막대, 물체를 각각 1 , 2 1 , 2 m 1 = 1 k g , m 1 = 1 k g , m 2 = 2 k g m 2 = 2 k g
따라서 ∑ i = 1 n m i = ∑ i = 1 2 m i = m 1 + m 2 = 1 k g + 2 k g = 3 k g i = 1 ∑ n m i = i = 1 ∑ 2 m i = m 1 + m 2 = 1 k g + 2 k g = 3 k g
막대의 가장 왼쪽 지점을 기준점이라 하면 r 1 = 4 m , r 1 = 4 m , r 2 = x max r 2 = x m a x
그러므로 ∑ i = 1 n m i r i = ∑ i = 1 2 m i r i , i = 1 ∑ n m i r i = i = 1 ∑ 2 m i r i , ∑ i = 1 n m i r i = m 1 r 1 + m 2 r 2 , i = 1 ∑ n m i r i = m 1 r 1 + m 2 r 2 , ∑ i = 1 n m i r i = ( 1 k g × 4 m ) + ( 2 k g × x max ) , i = 1 ∑ n m i r i = ( 1 k g × 4 m ) + ( 2 k g × x m a x ) , ∑ i = 1 n m i r i = 4 k g ⋅ m + 2 x max k g i = 1 ∑ n m i r i = 4 k g ⋅ m + 2 x m a x k g
질량 중심의 위치는 ∑ i = 1 n m i r i ∑ i = 1 n m i = ∑ i = 1 2 m i r i ∑ i = 1 2 m i = 4 k g ⋅ m + 2 x max k g 3 k g = 6 m i = 1 ∑ n m i i = 1 ∑ n m i r i = i = 1 ∑ 2 m i i = 1 ∑ 2 m i r i = 3 k g 4 k g ⋅ m + 2 x m a x k g = 6 m 4 k g ⋅ m + 2 x max k g 3 k g = 6 m , 3 k g 4 k g ⋅ m + 2 x m a x k g = 6 m , 4 k g ⋅ m + 2 x max k g = 18 k g ⋅ m , 4 k g ⋅ m + 2 x m a x k g = 1 8 k g ⋅ m , 4 m + 2 x max = 18 m , 4 m + 2 x m a x = 1 8 m , 2 x max = 14 m , 2 x m a x = 1 4 m , x max = 7 m x m a x = 7 m
1번 문항 정답 및 해설 보기
정답: $2$
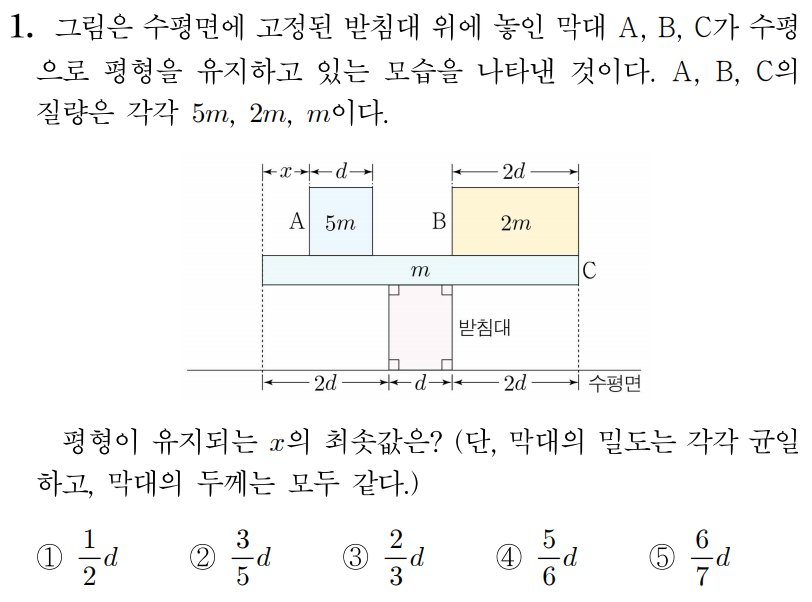
A , B , C A , B , C
A A 5 m g 5 m g B B 2 m g 2 m g C C m g m g
C C 0 0 C C 5 m g + 2 m g + m g = 8 m g 5 m g + 2 m g + m g = 8 m g
평형이 붕괴된 직후 C C C C
A , B , C A , B , C C C 0 0
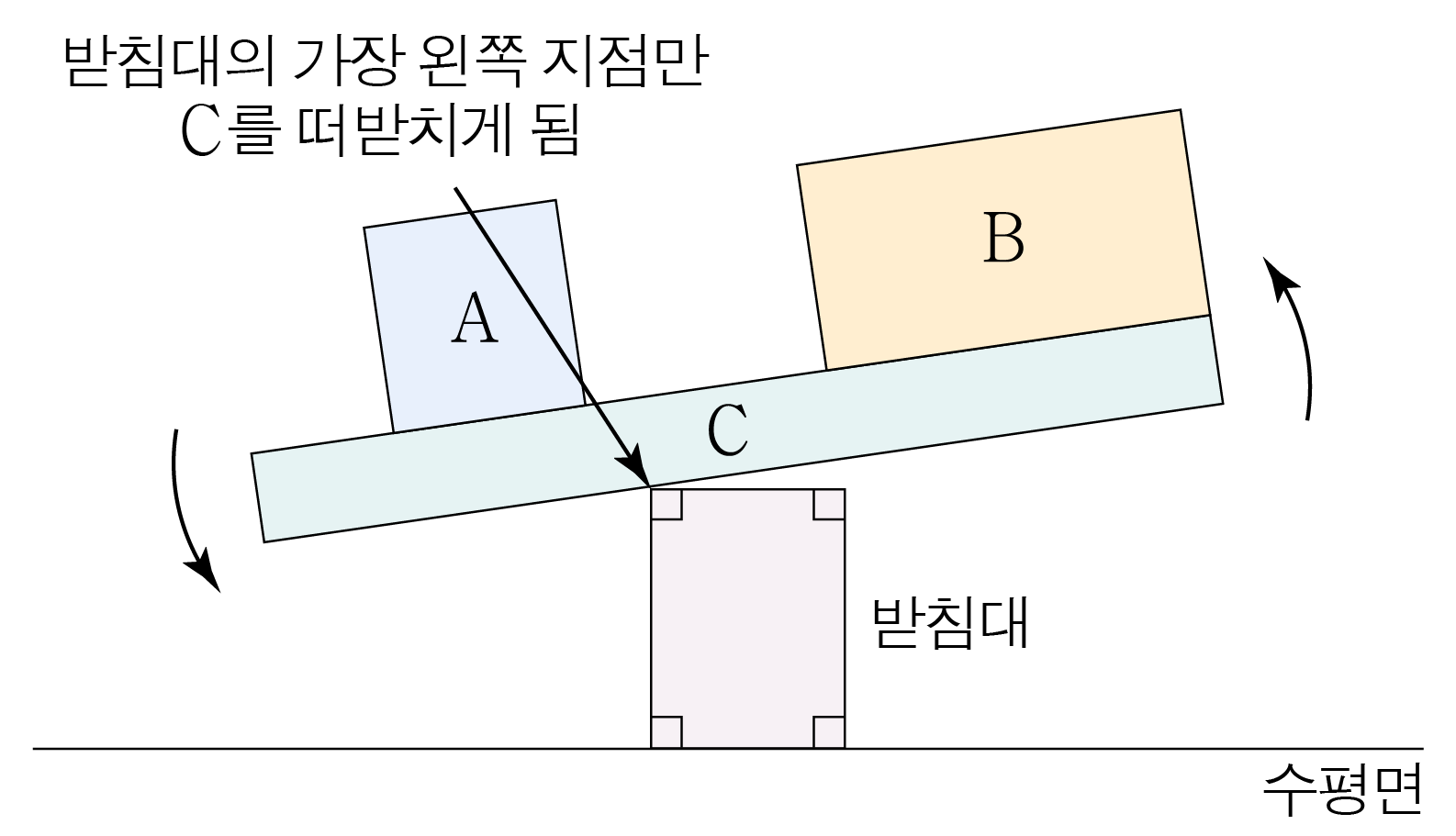
이때 아래 그림과 같이 받침대의 가장 왼쪽 지점만 C C x x C C
그러므로 x x x min x m i n
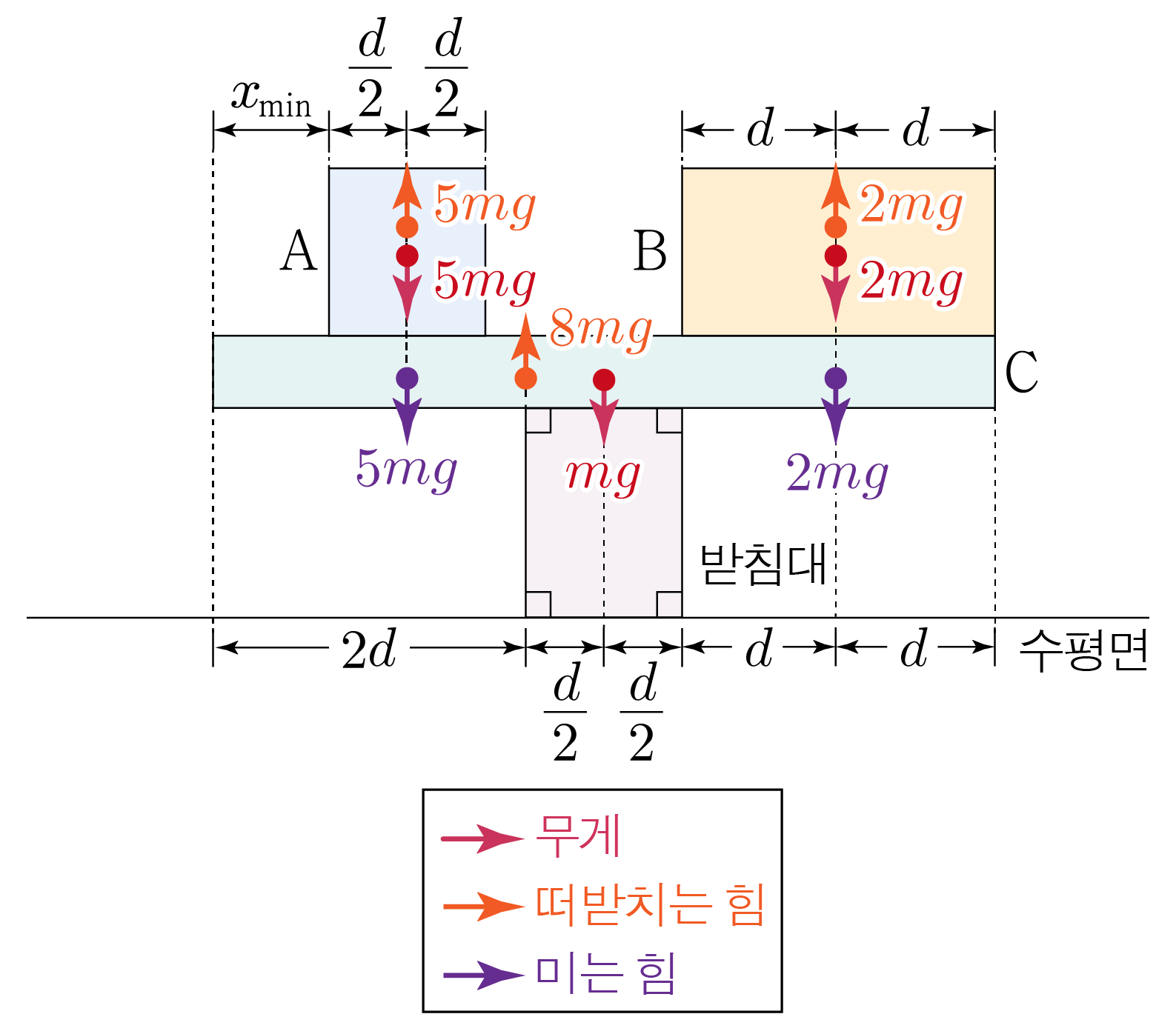
C C C C
A A C C − ( x min + d 2 ) × 5 m g = − 5 x min m g − 5 2 d m g − ( x m i n + 2 d ) × 5 m g = − 5 x m i n m g − 2 5 d m g B B C C − 4 d × 2 m g = − 8 d m g − 4 d × 2 m g = − 8 d m g C C − 5 2 d × m g = − 5 2 d m g − 2 5 d × m g = − 2 5 d m g 받침대가 C C 2 d × 8 m g = 16 d m g 2 d × 8 m g = 1 6 d m g
C C 0 0 − 5 x min m g − 5 2 d m g − 8 d m g − 5 2 d m g + 16 d m g = 0 − 5 x m i n m g − 2 5 d m g − 8 d m g − 2 5 d m g + 1 6 d m g = 0 − 5 x min − 5 2 d − 8 d − 5 2 d + 16 d = 0 , − 5 x m i n − 2 5 d − 8 d − 2 5 d + 1 6 d = 0 , − 5 x min − 5 d − 8 d + 16 d = 0 , − 5 x m i n − 5 d − 8 d + 1 6 d = 0 , − 5 x min − 13 d + 16 d = 0 , − 5 x m i n − 1 3 d + 1 6 d = 0 , − 5 x min + 3 d = 0 , − 5 x m i n + 3 d = 0 , 3 d = 5 x min , 3 d = 5 x m i n , x min = 3 5 d x m i n = 5 3 d
질량 중심으로 x min x m i n
x x C C A , B , C A , B , C
A , B , C A , B , C 1 , 2 , 3 1 , 2 , 3 m 1 = 5 m , m 1 = 5 m , m 2 = 2 m , m 2 = 2 m , m 3 = m m 3 = m
따라서 ∑ i = 1 n m i = ∑ i = 1 3 m i = m 1 + m 2 + m 3 = 5 m + 2 m + m = 8 m i = 1 ∑ n m i = i = 1 ∑ 3 m i = m 1 + m 2 + m 3 = 5 m + 2 m + m = 8 m
C C r 1 = x min + d 2 , r 1 = x m i n + 2 d , r 2 = 4 d , r 2 = 4 d , r 3 = 5 2 d r 3 = 2 5 d
그러므로 ∑ i = 1 n m i r i = ∑ i = 1 3 m i r i , i = 1 ∑ n m i r i = i = 1 ∑ 3 m i r i , ∑ i = 1 n m i r i = m 1 r 1 + m 2 r 2 + m 3 r 3 , i = 1 ∑ n m i r i = m 1 r 1 + m 2 r 2 + m 3 r 3 , ∑ i = 1 n m i r i = 5 m × ( x min + d 2 ) + ( 2 m × 4 d ) + ( m × 5 2 d ) , i = 1 ∑ n m i r i = 5 m × ( x m i n + 2 d ) + ( 2 m × 4 d ) + ( m × 2 5 d ) , ∑ i = 1 n m i r i = ( 5 m x min + 5 2 m d ) + 8 m d + 5 2 m d , i = 1 ∑ n m i r i = ( 5 m x m i n + 2 5 m d ) + 8 m d + 2 5 m d , ∑ i = 1 n m i r i = 5 m x min + 13 m d i = 1 ∑ n m i r i = 5 m x m i n + 1 3 m d
질량 중심의 위치는 ∑ i = 1 n m i r i ∑ i = 1 n m i = ∑ i = 1 3 m i r i ∑ i = 1 3 m i = 5 m x min + 13 m d 8 m = 2 d i = 1 ∑ n m i i = 1 ∑ n m i r i = i = 1 ∑ 3 m i i = 1 ∑ 3 m i r i = 8 m 5 m x m i n + 1 3 m d = 2 d 5 m x min + 13 m d 8 m = 2 d , 8 m 5 m x m i n + 1 3 m d = 2 d , 5 x min + 13 d = 16 d , 5 x m i n + 1 3 d = 1 6 d , 5 x min = 3 d , 5 x m i n = 3 d , x min = 3 5 d x m i n = 5 3 d
따라서 정답은 2 2
2번 문항 정답 및 해설 보기
정답: $3$
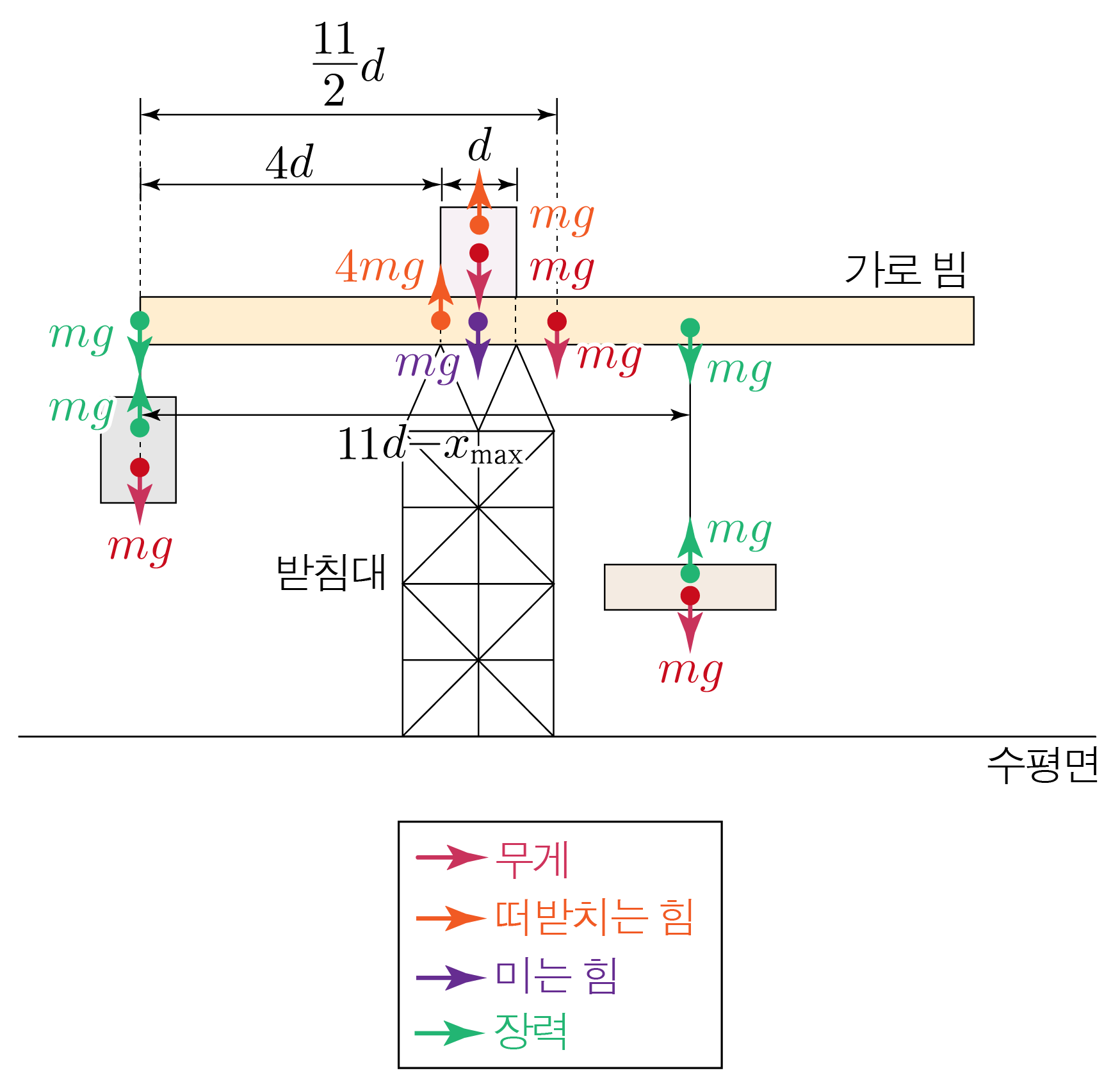
물체와 가로 빔의 무게를 구하면 아래와 같다.
가로 빔의 왼쪽에 매달린 물체의 무게: m g m g
가로 빔의 오른쪽에 매달린 물체의 무게: m g m g
가로 빔 위에 놓인 물체의 무게: m g m g
가로 빔의 무게: m g m g
가로 빔에 작용하는 알짜힘이 0 0 m g + m g + m g + m g = 4 m g m g + m g + m g + m g = 4 m g
1. 1 . x x
평형이 붕괴된 직후 가로 빔의 회전 방향을 통해 붕괴 직전 가로 빔에 작용하는 힘을 구해보자.
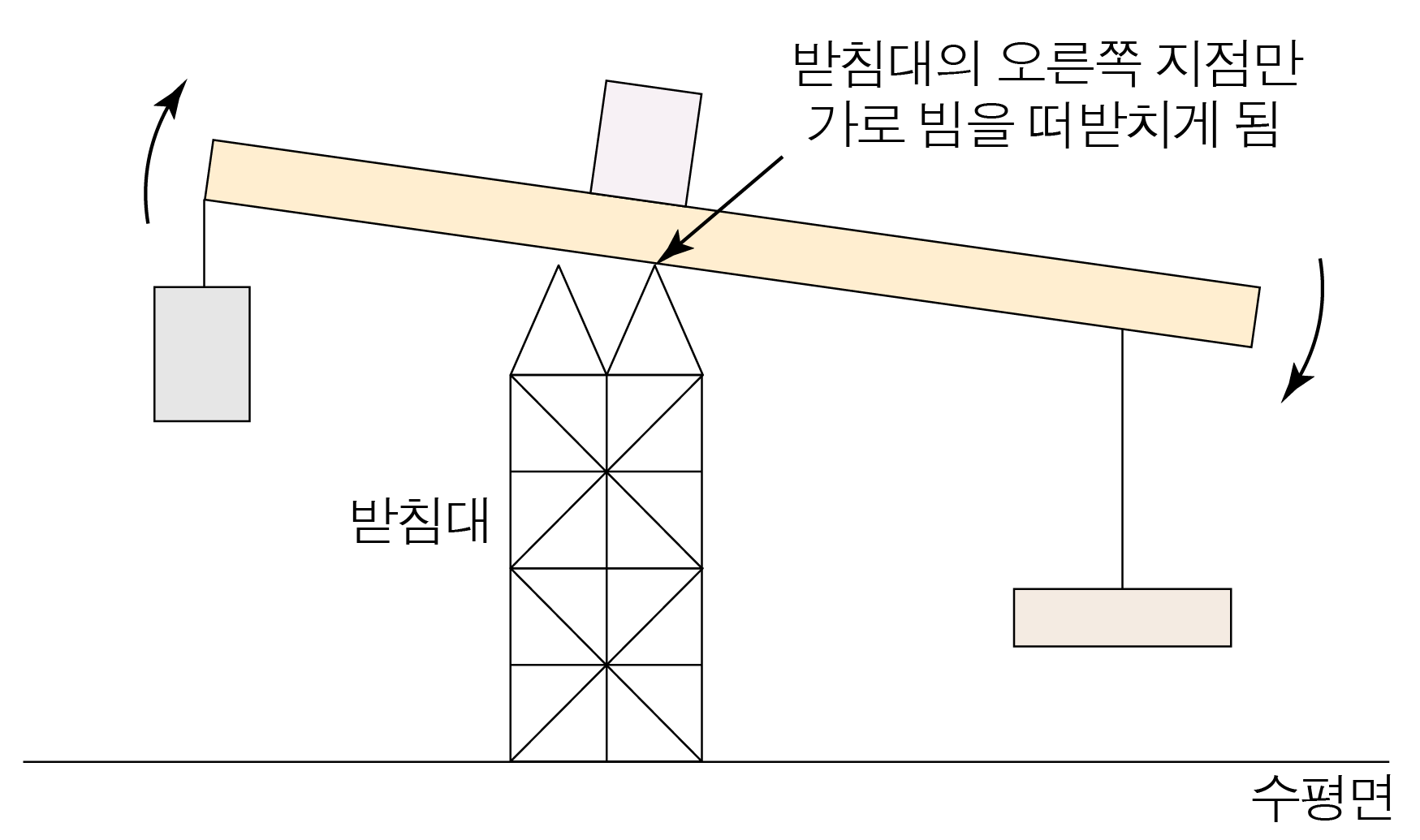
가로 빔과 물체를 하나의 계로 볼 때, 계의 질량 중심이 가로 빔과 받침대가 맞닿아 있는 부분 중 오른쪽 지점보다 오른쪽으로 치우치면 가로 빔에 작용하는 돌림힘의 합이 0 0
이때 아래 그림과 같이 받침대의 오른쪽 지점만 가로 빔을 떠받치게 되므로,x x 0 0
그러므로 x x x min x m i n
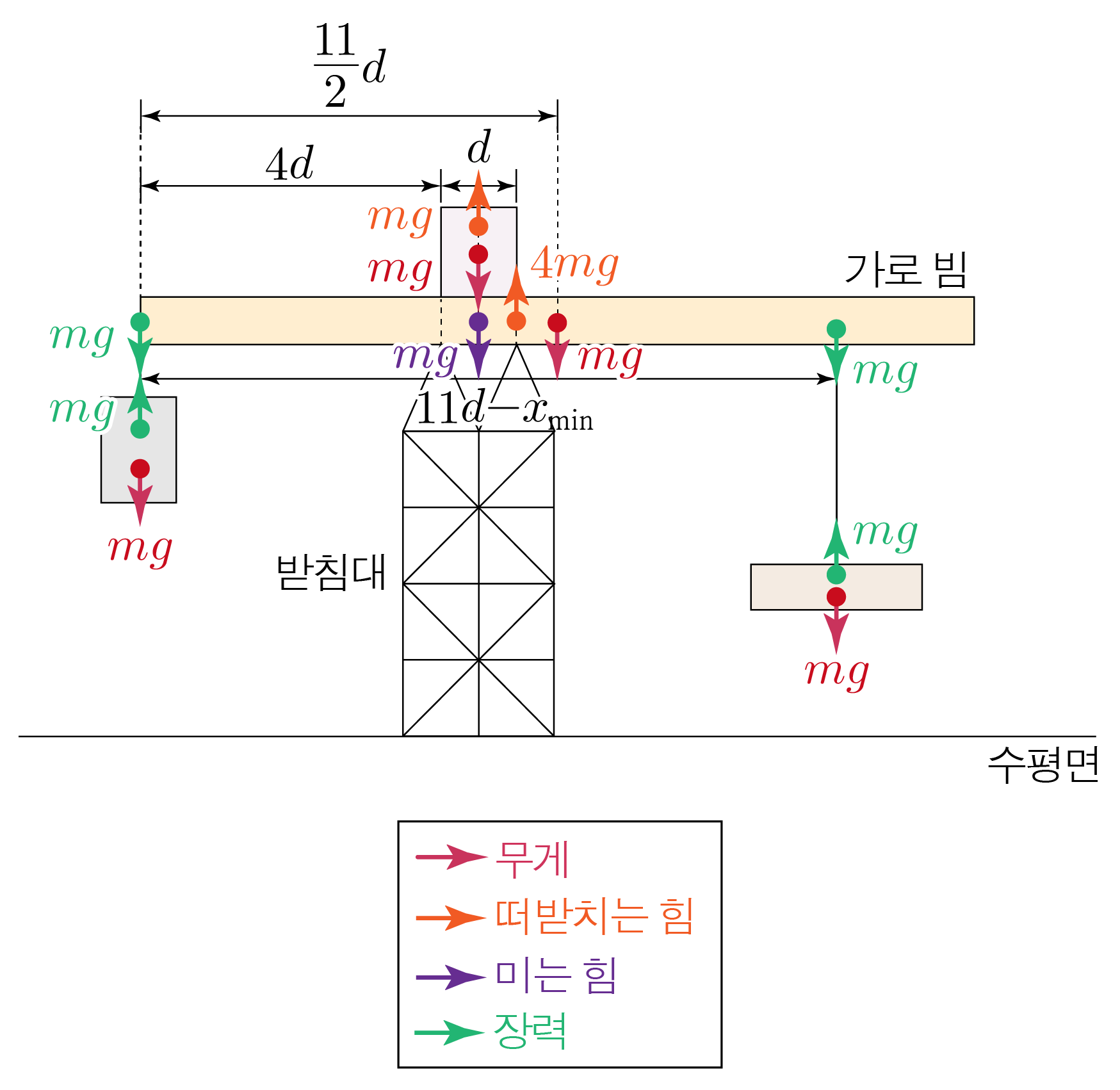
가로 빔의 가장 왼쪽 지점을 기준점으로 할 때, 가로 빔에 작용하는 각 힘에 의한 돌림힘을 구하면 아래와 같다.
가로 빔 위에 놓인 물체가 미는 힘에 의한 돌림힘:− ( 4 d + d 2 ) × m g = − 9 2 d m g − ( 4 d + 2 d ) × m g = − 2 9 d m g
왼쪽 줄이 당기는 힘에 의한 돌림힘:0 × m g = 0 0 × m g = 0
오른쪽 줄이 당기는 힘에 의한 돌림힘:− ( 11 d − x min ) × m g = − 11 d m g + x min m g − ( 1 1 d − x m i n ) × m g = − 1 1 d m g + x m i n m g
가로 빔의 무게에 의한 돌림힘:− 11 2 d × m g = − 11 2 d m g − 2 1 1 d × m g = − 2 1 1 d m g
받침대가 가로 빔을 떠받치는 힘에 의한 돌림힘:5 d × 4 m g = 20 d m g 5 d × 4 m g = 2 0 d m g
가로 빔에 작용하는 돌림힘의 합이 0 0 − 9 2 d m g + 0 − 11 d m g + x min m g − 11 2 d m g + 20 d m g = 0 , − 2 9 d m g + 0 − 1 1 d m g + x m i n m g − 2 1 1 d m g + 2 0 d m g = 0 , − 9 2 d − 11 d + x min − 11 2 d + 20 d = 0 , − 2 9 d − 1 1 d + x m i n − 2 1 1 d + 2 0 d = 0 , − 10 d − 11 d + x min + 20 d = 0 , − 1 0 d − 1 1 d + x m i n + 2 0 d = 0 , − 21 d + x min + 20 d = 0 , − 2 1 d + x m i n + 2 0 d = 0 , − d + x min = 0 , − d + x m i n = 0 , x min = d x m i n = d
질량 중심으로 x min x m i n
x x
가로 빔, 가로 빔의 왼쪽에 줄로 연결된 물체, 가로 빔의 오른쪽에 줄로 연결된 물체, 가로 빔 위의 물체를 각각 1 , 2 , 3 , 4 1 , 2 , 3 , 4 m 1 = m 2 = m 3 = m 4 = m m 1 = m 2 = m 3 = m 4 = m
따라서 ∑ i = 1 n m i = ∑ i = 1 4 m i = m 1 + m 2 + m 3 + m 4 = 4 m i = 1 ∑ n m i = i = 1 ∑ 4 m i = m 1 + m 2 + m 3 + m 4 = 4 m
가로 빔의 가장 왼쪽 지점을 기준점이라 하면r 1 = 11 2 d , r 1 = 2 1 1 d , r 2 = 0 , r 2 = 0 , r 3 = 11 d − x min , r 3 = 1 1 d − x m i n , r 4 = 4 d + d 2 = 9 2 d r 4 = 4 d + 2 d = 2 9 d
그러므로 ∑ i = 1 n m i r i = ∑ i = 1 4 m i r i , i = 1 ∑ n m i r i = i = 1 ∑ 4 m i r i , ∑ i = 1 n m i r i = m 1 r 1 + m 2 r 2 + m 3 r 3 + m 4 r 4 , i = 1 ∑ n m i r i = m 1 r 1 + m 2 r 2 + m 3 r 3 + m 4 r 4 , ∑ i = 1 n m i r i = m × 11 2 d + m × 0 + m × ( 11 d − x min ) + m × 9 2 d , i = 1 ∑ n m i r i = m × 2 1 1 d + m × 0 + m × ( 1 1 d − x m i n ) + m × 2 9 d , ∑ i = 1 n m i r i = 11 2 m d + 11 m d − x min m + 9 2 m d , i = 1 ∑ n m i r i = 2 1 1 m d + 1 1 m d − x m i n m + 2 9 m d , ∑ i = 1 n m i r i = 33 2 m d − x min m + 9 2 m d , i = 1 ∑ n m i r i = 2 3 3 m d − x m i n m + 2 9 m d , ∑ i = 1 n m i r i = 21 m d − x min m i = 1 ∑ n m i r i = 2 1 m d − x m i n m
질량 중심의 위치는 ∑ i = 1 n m i r i ∑ i = 1 n m i = ∑ i = 1 4 m i r i ∑ i = 1 4 m i = 21 m d − x min m 4 m = 5 d i = 1 ∑ n m i i = 1 ∑ n m i r i = i = 1 ∑ 4 m i i = 1 ∑ 4 m i r i = 4 m 2 1 m d − x m i n m = 5 d 21 m d − x min m = 20 m d , 2 1 m d − x m i n m = 2 0 m d , 21 d − x min = 20 d , 2 1 d − x m i n = 2 0 d , − x min = − d , − x m i n = − d , x min = d x m i n = d
2. 2 . x x
평형이 붕괴된 직후 가로 빔의 회전 방향을 통해 붕괴 직전 가로 빔에 작용하는 힘을 구해보자.
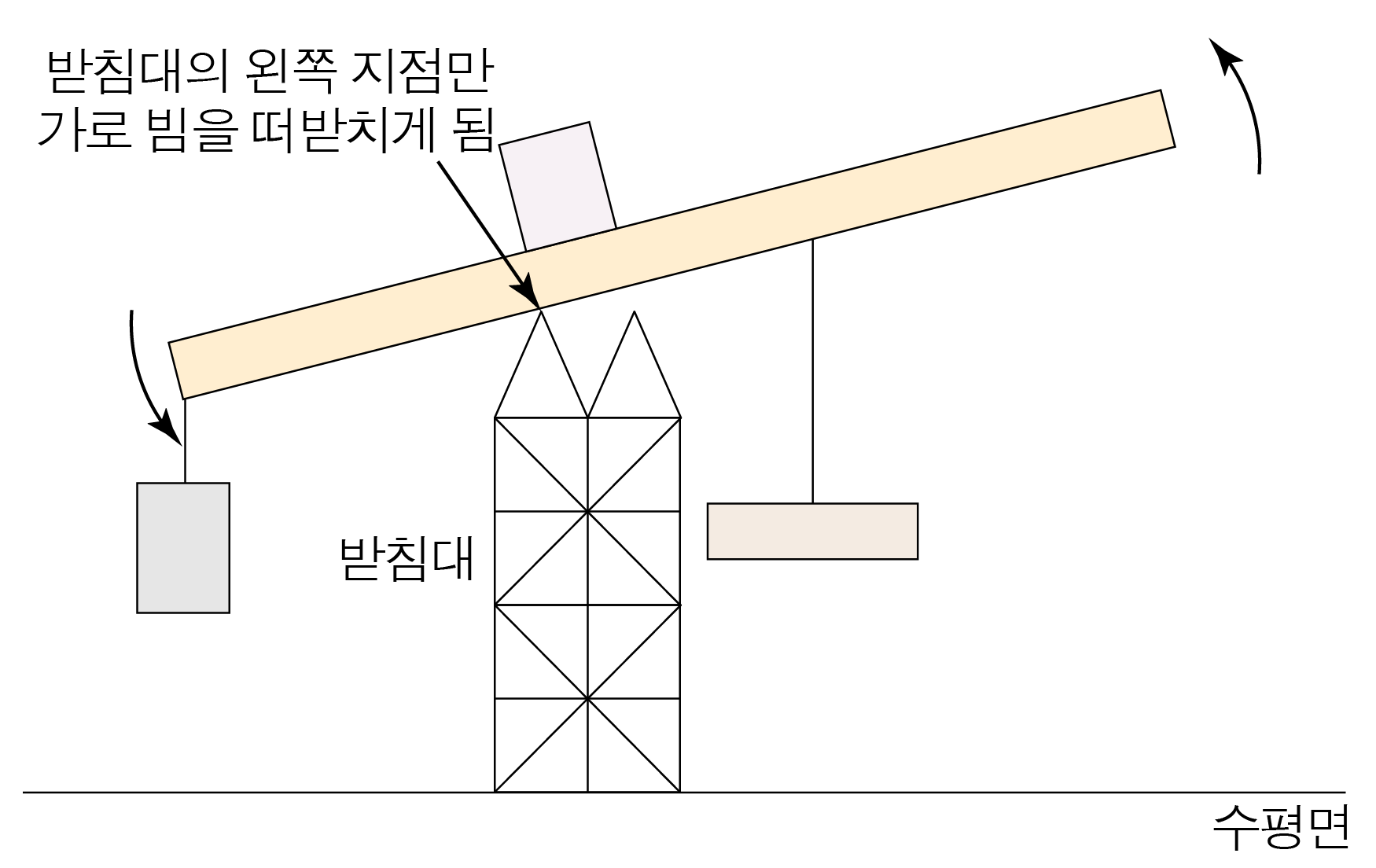
가로 빔과 물체를 하나의 계로 볼 때, 계의 질량 중심이 가로 빔과 받침대가 맞닿아 있는 부분 중 왼쪽 지점보다 왼쪽으로 치우치면 가로 빔에 작용하는 돌림힘의 합이 0 0
이때 아래 그림과 같이 받침대의 왼쪽 지점만 가로 빔을 떠받치게 되므로,x x 0 0
그러므로 x x x max x m a x
가로 빔의 가장 왼쪽 지점을 기준점으로 할 때, 가로 빔에 작용하는 각 힘에 의한 돌림힘을 구하면 아래와 같다.
가로 빔 위에 놓인 물체가 미는 힘에 의한 돌림힘:− ( 4 d + d 2 ) × m g = − 9 2 d m g − ( 4 d + 2 d ) × m g = − 2 9 d m g
왼쪽 줄이 당기는 힘에 의한 돌림힘:0 × m g = 0 0 × m g = 0
오른쪽 줄이 당기는 힘에 의한 돌림힘:− ( 11 d − x max ) × m g = − 11 d m g + x max m g − ( 1 1 d − x m a x ) × m g = − 1 1 d m g + x m a x m g
가로 빔의 무게에 의한 돌림힘:− 11 2 d × m g = − 11 2 d m g − 2 1 1 d × m g = − 2 1 1 d m g
받침대가 가로 빔을 떠받치는 힘에 의한 돌림힘:4 d × 4 m g = 16 d m g 4 d × 4 m g = 1 6 d m g
가로 빔에 작용하는 돌림힘의 합이 0 0 − 9 2 d m g + 0 − 11 d m g + x max m g − 11 2 d m g + 16 d m g = 0 , − 2 9 d m g + 0 − 1 1 d m g + x m a x m g − 2 1 1 d m g + 1 6 d m g = 0 , − 9 2 d − 11 d + x max − 11 2 d + 16 d = 0 , − 2 9 d − 1 1 d + x m a x − 2 1 1 d + 1 6 d = 0 , − 10 d − 11 d + x max + 16 d = 0 , − 1 0 d − 1 1 d + x m a x + 1 6 d = 0 , − 21 d + x max + 16 d = 0 , − 2 1 d + x m a x + 1 6 d = 0 , − 5 d + x max = 0 , − 5 d + x m a x = 0 , x max = 5 d x m a x = 5 d
질량 중심으로 x max x m a x
x x
가로 빔, 가로 빔의 왼쪽에 줄로 연결된 물체, 가로 빔의 오른쪽에 줄로 연결된 물체, 가로 빔 위의 물체를 각각 1 , 2 , 3 , 4 1 , 2 , 3 , 4 m 1 = m 2 = m 3 = m 4 = m m 1 = m 2 = m 3 = m 4 = m
따라서 ∑ i = 1 n m i = ∑ i = 1 4 m i = m 1 + m 2 + m 3 + m 4 = 4 m i = 1 ∑ n m i = i = 1 ∑ 4 m i = m 1 + m 2 + m 3 + m 4 = 4 m
아래쪽 가로 빔의 가장 왼쪽 지점을 기준점이라 하면 r 1 = 11 2 d , r 1 = 2 1 1 d , r 2 = 0 , r 2 = 0 , r 3 = 11 d − x max , r 3 = 1 1 d − x m a x , r 4 = 4 d + d 2 = 9 2 d r 4 = 4 d + 2 d = 2 9 d
그러므로 ∑ i = 1 n m i r i = ∑ i = 1 4 m i r i , i = 1 ∑ n m i r i = i = 1 ∑ 4 m i r i , ∑ i = 1 n m i r i = m 1 r 1 + m 2 r 2 + m 3 r 3 + m 4 r 4 , i = 1 ∑ n m i r i = m 1 r 1 + m 2 r 2 + m 3 r 3 + m 4 r 4 , ∑ i = 1 n m i r i = m × 11 2 d + m × 0 + m × ( 11 d − x max ) + m × 9 2 d , i = 1 ∑ n m i r i = m × 2 1 1 d + m × 0 + m × ( 1 1 d − x m a x ) + m × 2 9 d , ∑ i = 1 n m i r i = 11 2 m d + 11 m d − x max m + 9 2 m d , i = 1 ∑ n m i r i = 2 1 1 m d + 1 1 m d − x m a x m + 2 9 m d , ∑ i = 1 n m i r i = 33 2 m d − x max m + 9 2 m d , i = 1 ∑ n m i r i = 2 3 3 m d − x m a x m + 2 9 m d , ∑ i = 1 n m i r i = 21 m d − x max m i = 1 ∑ n m i r i = 2 1 m d − x m a x m
질량 중심의 위치는 ∑ i = 1 n m i r i ∑ i = 1 n m i = ∑ i = 1 4 m i r i ∑ i = 1 4 m i = 21 m d − x max m 4 m = 4 d i = 1 ∑ n m i i = 1 ∑ n m i r i = i = 1 ∑ 4 m i i = 1 ∑ 4 m i r i = 4 m 2 1 m d − x m a x m = 4 d 21 m d − x max m = 16 m d , 2 1 m d − x m a x m = 1 6 m d , 21 d − x max = 16 d , 2 1 d − x m a x = 1 6 d , − x max = − 5 d , − x m a x = − 5 d , x max = 5 d x m a x = 5 d
그러므로 x min + x max = d + 5 d = 6 d x m i n + x m a x = d + 5 d = 6 d
따라서 정답은 3 3