¶ 지식 정보
¶ 계
분석하고자 하는 대상 전체를 하나로 묶어서 부른 것이다.
¶ 강체
힘을 가해도 형태가 변하지 않는 물체이다.
¶ 관성 모멘트
회전축을 기준으로 같은 각속도로 회전하는 물체(강체)가 총 개 있고,
번째 물체의 질량을 , 회전축으로부터 번째 물체까지의 거리를 라 할 때
이 물체들로 이루어진 계의 관성 모멘트는 이다.
기본 단위는 이고, 기호로는 로 나타낸다.
¶ 관성 모멘트 예시
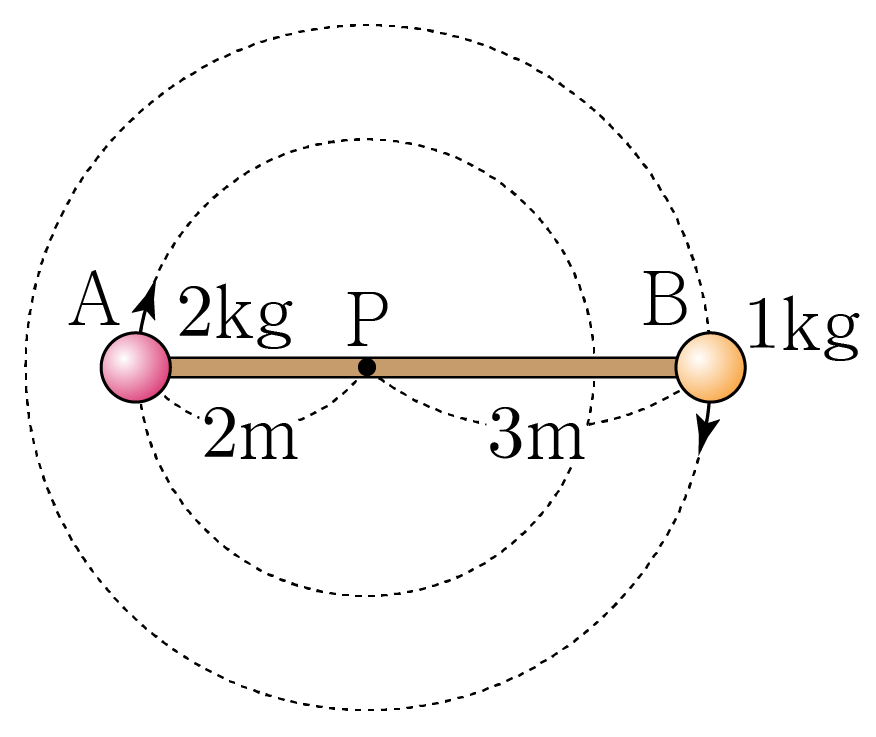
그림은 물체 , 가 막대 끝에 고정되어 점 를 중심으로 시계 방향으로 회전하고 있는 모습을 나타낸 것이다.
, 의 질량은 각각 , 이다. , , 막대로 이루어진 계의 관성 모멘트 를 구해보자. (단, 물체의 크기와 막대의 질량은 무시한다.)
회전축을 기준으로 같은 각속도로 회전하는 물체가 총 개 있고,
번째 물체의 질량을 , 회전축으로부터 번째 물체까지의 거리를 , 이 물체들로 이루어진 계의 관성 모멘트 이다.
막대의 질량은 무시하므로 계의 관성 모멘트는 와 만 고려하면 된다.
물체가 총 개이므로 이고, , 를 각각 , 번째 물체라 하면 , 이다.
회전축(화면(종이면)에 수직이고 를 지나는 선)으로부터 물체까지의 거리는 , 이다.
그러므로
이다.
¶ 적용 문항
¶ 1번 문항

정답: $4$
회전축을 기준으로 같은 각속도로 회전하는 물체가 총 개 있고,
번째 물체의 질량을 , 회전축으로부터 번째 물체까지의 거리를 , 이 물체들로 이루어진 계의 관성 모멘트 이다.
막대의 질량은 무시하므로 계의 관성 모멘트는 ~만 고려하면 된다.
물체가 총 개이므로 이고, , , , 를 각각 , , , 번째 물체라 하면
, , , 이다.
- 회전축이 축일 때 관성 모멘트 구하기:
축으로부터 물체까지의 거리는 , , , 이다.
그러므로 회전축이 축일 때 관성 모멘트를 라 하면,
이다.
- 회전축이 축일 때 관성 모멘트 구하기:
축으로부터 물체까지의 거리는 , , , 이다.
그러므로 회전축이 축일 때 관성 모멘트를 라 하면,
이다.
계의 관성 모멘트는 회전축이 축일 때와 축일 때가 같으므로
이다.
따라서 정답은 번이다.
¶ 2번 문항
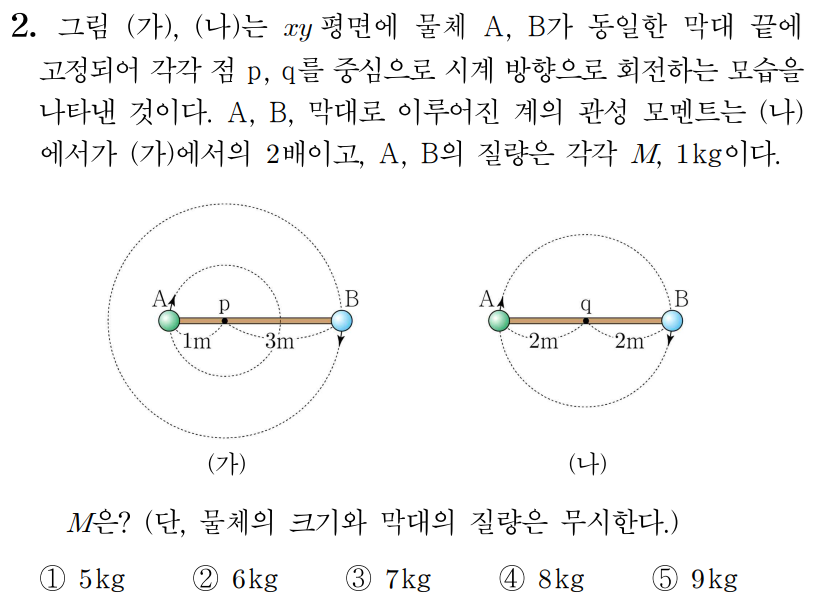
정답: $3$
회전축을 기준으로 같은 각속도로 회전하는 물체가 총 개 있고,
번째 물체의 질량을 , 회전축으로부터 번째 물체까지의 거리를 , 이 물체들로 이루어진 계의 관성 모멘트 이다.
막대의 질량은 무시하므로 계의 관성 모멘트는 와 만 고려하면 된다.
물체가 총 개이므로 이고, , 를 각각 , 번째 물체라 하면 , 이다.
- (가)에서 계의 관성 모멘트 구하기:
회전축(화면(종이면)에 수직이고 를 지나는 선)으로부터 물체까지의 거리는 , 이다.
그러므로 (가)에서 관성 모멘트를 라 하면,
이다.
- (나)에서 계의 관성 모멘트 구하기:
회전축(화면(종이면)에 수직이고 를 지나는 선)으로부터 물체까지의 거리는 , 이다.
그러므로 (나)에서 관성 모멘트를 라 하면,
이다.
계의 관성 모멘트는 (나)에서가 (가)에서의 배이므로
이다.
따라서 정답은 번이다.




