화학 반응에서 반응물과 생성물의 양적 관계에 관한 것이다.m o l m o l m o l m o l m o l m o l
질량(g g → m o l → m o l 64 g 6 4 g O 2 O 2 m o l m o l 32 g / m o l 3 2 g / m o l 64 g × 1 m o l 32 g = 2 m o l 6 4 g × 3 2 g 1 m o l = 2 m o l
m o l → m o l → g g 2 m o l 2 m o l O 2 O 2 32 g / m o l 3 2 g / m o l 2 m o l × 32 g 1 m o l = 64 g 2 m o l × 1 m o l 3 2 g = 6 4 g
기체의 부피(L L → m o l → m o l 22.4 L / m o l 2 2 . 4 L / m o l
m o l → m o l → L L m o l m o l 22.4 L / m o l 2 2 . 4 L / m o l
기체의 부피(L L → m o l → m o l 67.2 L 6 7 . 2 L O 2 ( g ) O 2 ( g ) m o l m o l 67.2 L × 1 m o l 22.4 L = 3 m o l 6 7 . 2 L × 2 2 . 4 L 1 m o l = 3 m o l
m o l → m o l → L L 3 m o l 3 m o l O 2 ( g ) O 2 ( g ) 3 m o l × 22.4 L 1 m o l = 67.2 L 3 m o l × 1 m o l 2 2 . 4 L = 6 7 . 2 L
입자 수(개) → m o l → m o l N A = 6.02 × 1 0 23 N A = 6 . 0 2 × 1 0 2 3 / m o l / m o l
m o l → m o l → m o l m o l N A = 6.02 × 1 0 23 N A = 6 . 0 2 × 1 0 2 3 / m o l / m o l
입자 수(개) → m o l → m o l O 2 O 2 12.04 × 1 0 23 1 2 . 0 4 × 1 0 2 3 m o l m o l 12.04 × 1 0 23 1 2 . 0 4 × 1 0 2 3 ÷ N A = 12.04 × 1 0 23 ÷ N A = 1 2 . 0 4 × 1 0 2 3 × 1 m o l 6.02 × 1 0 23 개 = 2 m o l × 6 . 0 2 × 1 0 2 3 개 1 m o l = 2 m o l
m o l → m o l → 2 m o l 2 m o l O 2 O 2 2 m o l × N A = 2 m o l × 6.02 × 1 0 23 개 1 m o l = 12.04 × 1 0 23 2 m o l × N A = 2 m o l × 1 m o l 6 . 0 2 × 1 0 2 3 개 = 1 2 . 0 4 × 1 0 2 3
화학 반응에서 다른 반응물에 비해 먼저 소모되어 생성물의 양을 제한하는 반응물이다.
화학 반응에서 다른 반응물에 비해 필요한 양을 초과하는 반응물이다.
다음은 철(F e F e O 2 O 2 Ⅲ Ⅲ
4 F e ( s ) + 3 O 2 ( g ) → 2 F e 2 O 3 ( s ) 4 F e ( s ) + 3 O 2 ( g ) → 2 F e 2 O 3 ( s )
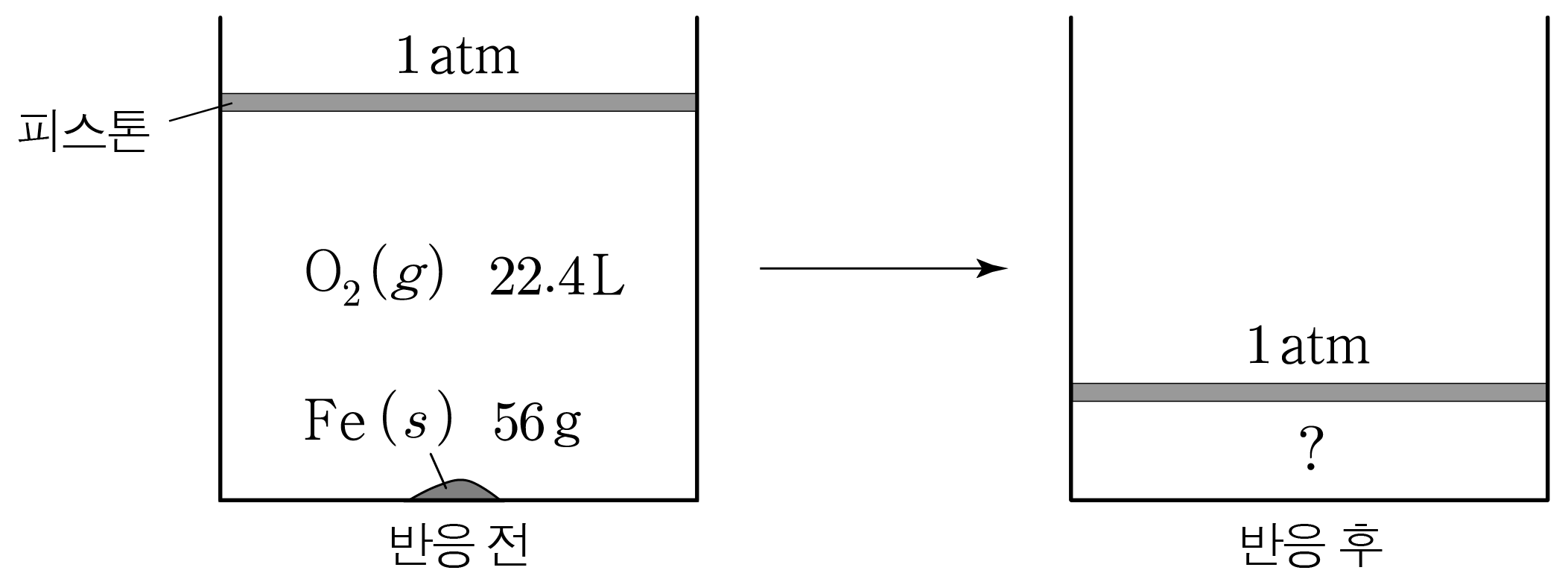
그림은 1 a t m 1 a t m F e ( s ) 56 g , F e ( s ) 5 6 g , O 2 ( g ) 22.4 L O 2 ( g ) 2 2 . 4 L 0 ∘ C 0 ∘ C F e F e O 2 O 2 F e 2 O 3 F e 2 O 3 56 g / m o l 5 6 g / m o l 32 g / m o l 3 2 g / m o l 160 g / m o l 1 6 0 g / m o l
반응 전 반응물의 m o l m o l
F e ( s ) F e ( s ) m o l m o l O 2 ( g ) O 2 ( g ) m o l m o l
반응 분석하기:
계수비만큼의 반응물이 반응하고 생성물이 생성되므로,F e ( s ) F e ( s ) 1 m o l , 1 m o l , O 2 ( g ) O 2 ( g ) 1 m o l × 3 4 = 3 4 m o l 1 m o l × 4 3 = 4 3 m o l F e 2 O 3 ( s ) F e 2 O 3 ( s ) 1 × 2 4 = 1 2 m o l 1 × 4 2 = 2 1 m o l
이때 F e ( s ) F e ( s ) O 2 ( g ) O 2 ( g )
따라서 반응을 정리하면 아래 표와 같다.
반응식
$4\mathrm{Fe}(s)$
$+$
$3\mathrm{O_{2}}(g)$
$\rightarrow$
$2\mathrm{Fe_{2}O_{3}}(s)$
반응 전 몰 수
$1$
$1$
$0$
반응 몰 수
$-1$
$-\frac{3}{4}$
$+\frac{1}{2}$
반응 후 몰 수
$0$
$\frac{1}{4}$
$\frac{1}{2}$
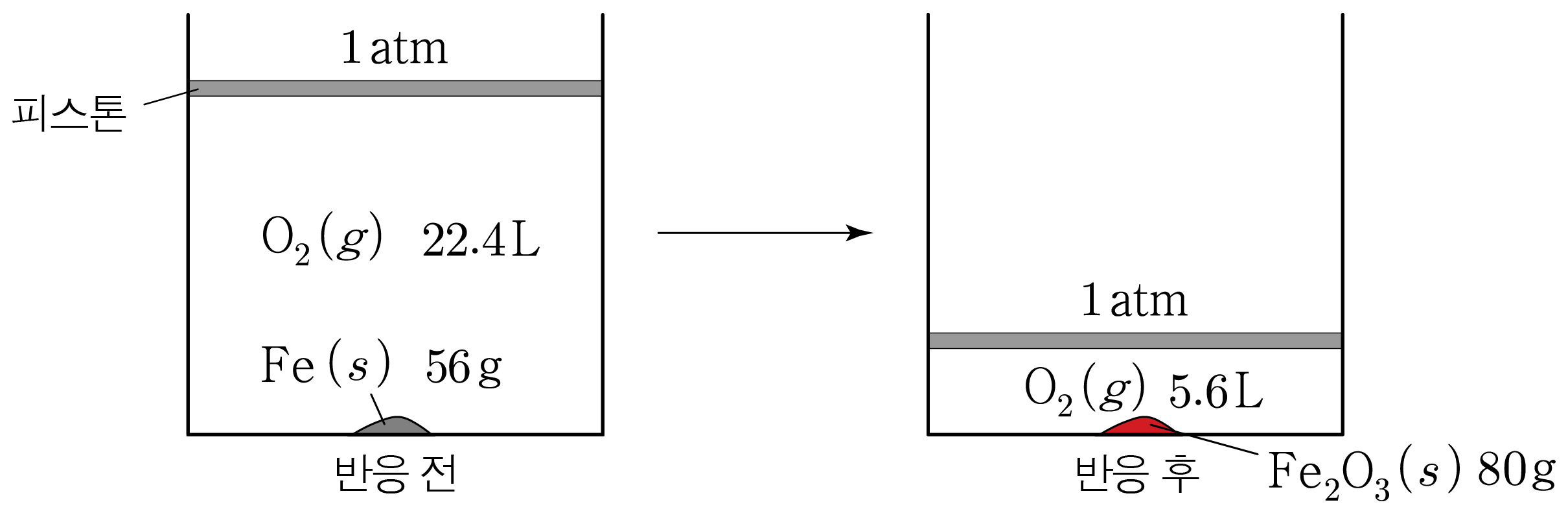
반응 후 분석하기:
생성된 F e 2 O 3 ( s ) F e 2 O 3 ( s ) 0.5 m o l × 160 g m o l = 80 g 0 . 5 m o l × m o l 1 6 0 g = 8 0 g
남은 O 2 ( g ) O 2 ( g ) O 2 ( g ) O 2 ( g ) 1 m o l − 3 4 m o l = 1 4 m o l 1 m o l − 4 3 m o l = 4 1 m o l 1 4 m o l × 22.4 L 1 m o l = 5.6 L 4 1 m o l × 1 m o l 2 2 . 4 L = 5 . 6 L
그러므로 위에 구한 내용을 그림에 나타내면 아래와 같다.
1번 문항 정답 및 해설 보기
정답: $3$
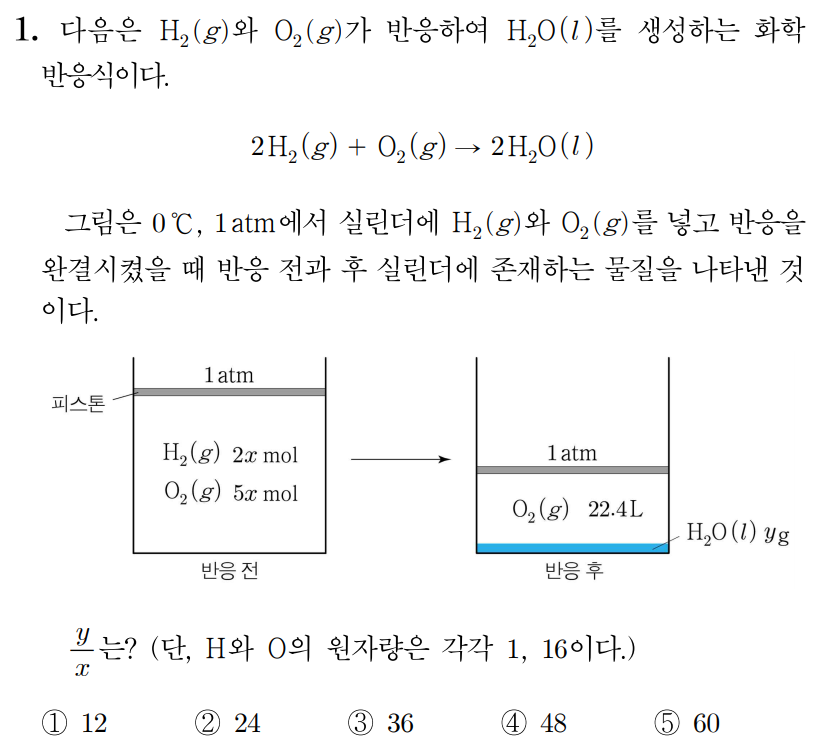
H 2 ( g ) H 2 ( g )
반응식
$2\mathrm{H_{2}}(g)$
$+$
$\mathrm{O_{2}}(g)$
$\rightarrow$
$2\mathrm{H_{2}O}(l)$
반응 전 몰 수
$2x$
$5x$
$0$
반응 몰 수
$-2x$
$-x$
$+2x$
반응 후 몰 수
$0$
$4x$
$2x$
0 ∘ C , 0 ∘ C , 1 a t m 1 a t m 1 m o l 1 m o l 22.4 L 2 2 . 4 L O 2 ( g ) O 2 ( g ) 1 m o l 1 m o l
그러므로 4 x = 1 , 4 x = 1 , x = 1 4 x = 4 1 H 2 O ( l ) H 2 O ( l ) 1 4 m o l × 2 = 1 2 m o l 4 1 m o l × 2 = 2 1 m o l
H 2 O H 2 O 1 1 H H 2 2 16 1 6 O O 1 1 1 × 2 + 16 = 18 1 × 2 + 1 6 = 1 8
이때 1 m o l 1 m o l g g H 2 O 1 m o l H 2 O 1 m o l 18 g 1 8 g H 2 O 1 2 m o l H 2 O 2 1 m o l 18 g × 1 2 = 9 g , 1 8 g × 2 1 = 9 g , y = 9 y = 9
x = 1 4 , x = 4 1 , y = 9 y = 9 y x = 36 x y = 3 6
따라서 답은 3 3
2번 문항 정답 및 해설 보기
정답: $1$
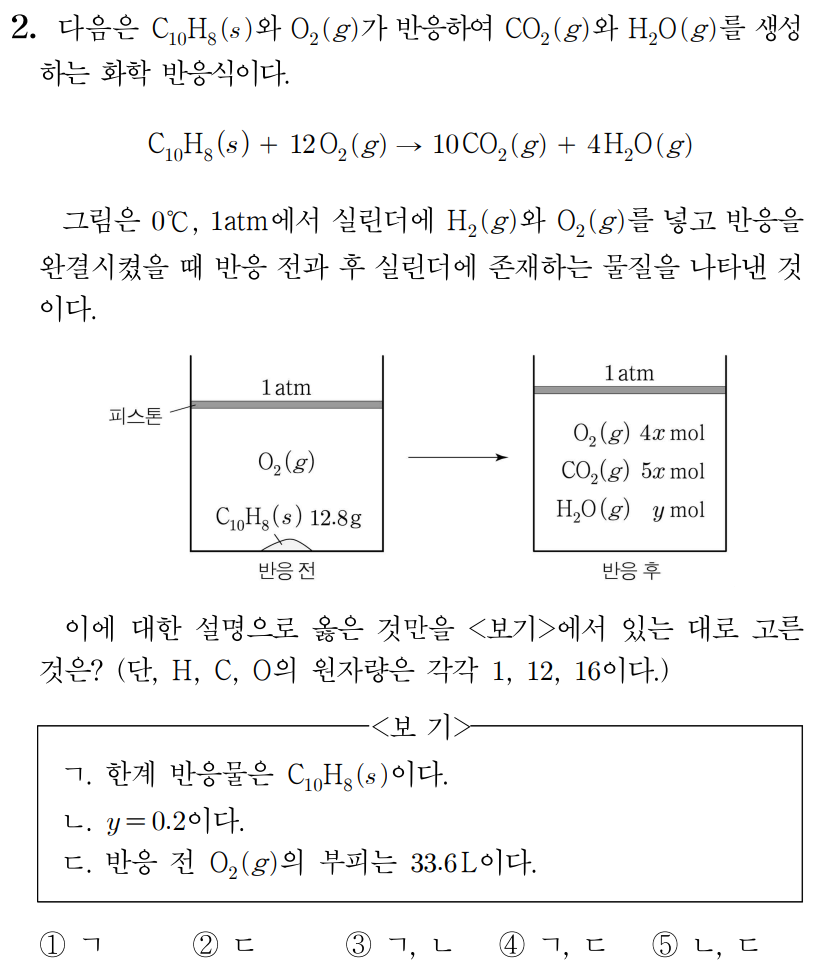
ㄱ. 화학 반응에서 C 10 H 8 ( s ) C 1 0 H 8 ( s ) O 2 ( g ) O 2 ( g ) C 10 H 8 ( s ) C 1 0 H 8 ( s ) O 2 ( g ) O 2 ( g )
ㄴ. C 10 H 8 C 1 0 H 8 12 1 2 C C 10 1 0 1 1 H H 8 8 12 × 10 + 1 × 8 = 128 1 2 × 1 0 + 1 × 8 = 1 2 8
그러므로 12.8 g 1 2 . 8 g C 10 H 8 C 1 0 H 8 12.8 g × 1 m o l 128 g = 0.1 m o l 1 2 . 8 g × 1 2 8 g 1 m o l = 0 . 1 m o l
C 10 H 8 C 1 0 H 8 0.1 m o l 0 . 1 m o l O 2 O 2 1.2 m o l 1 . 2 m o l C O 2 C O 2 H 2 O H 2 O 1 m o l , 1 m o l , 0.4 m o l 0 . 4 m o l
따라서 반응 전 O 2 ( g ) O 2 ( g ) a m o l a m o l
반응식
$\mathrm{C_{10}H_{8}}(s)$
$+$
$12\mathrm{O_{2}}(g)$
$\rightarrow$
$10\mathrm{CO_{2}}(g)$
$+$
$4\mathrm{H_{2}O}(g)$
반응 전 몰 수
$0.1$
$a$
$0$
$0$
반응 몰 수
$-0.1$
$-1.2$
$+1$
$+0.4$
반응 후 몰 수
$0$
$4x$
$5x$
$y$
이를 통해 a − 1.2 = 4 x , a − 1 . 2 = 4 x , 1 = 5 x , 1 = 5 x , y = 0.4 y = 0 . 4
ㄷ. a − 1.2 = 4 x , a − 1 . 2 = 4 x , 1 = 5 x 1 = 5 x x = 1 5 , x = 5 1 , a = 2 a = 2 O 2 ( g ) O 2 ( g ) 2 m o l 2 m o l 0 ∘ C , 0 ∘ C , 1 a t m 1 a t m 1 m o l 1 m o l 22.4 L 2 2 . 4 L O 2 ( g ) O 2 ( g ) 2 m o l × 22.4 L 1 m o l = 44.8 L 2 m o l × 1 m o l 2 2 . 4 L = 4 4 . 8 L
따라서 답은 1 1