물체의 역학적 에너지를 변화시키지 않는 힘이다.
물체의 역학적 에너지를 변화시키는 힘이다.
물체에 작용하는 알짜힘이 한 일은 물체의 운동 에너지 변화량과 같으며,
물체의 운동 방향과 알짜힘의 방향이 같은 경우 물체의 운동 에너지는 증가하며, 반대인 경우 감소한다.
물체의 운동 방향과 비보존력의 방향이 같은 경우 물체의 역학적 에너지는 증가하며, 반대인 경우 감소한다.
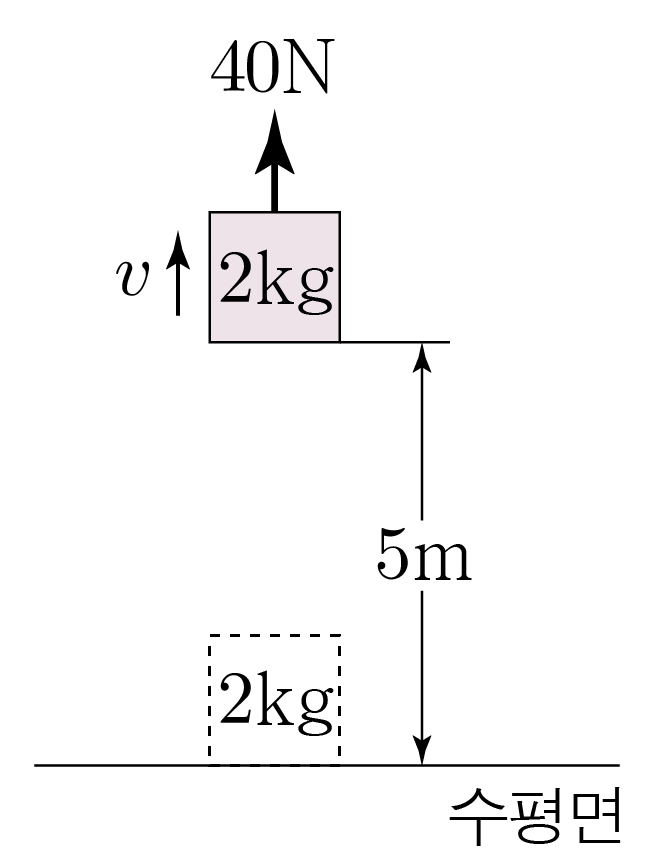
그림은 수평면에 정지해 있는 질량이 2 k g 2 k g 40 N 4 0 N 5 m 5 m v v 10 m / s 2 1 0 m / s 2
물체에 작용하는 알짜힘이 한 일은 물체의 운동 에너지 변화량과 같음을 활용하는 경우
물체에 연직 아래 방향으로 크기가 2 k g × 10 m / s 2 = 20 k g ⋅ m / s 2 = 20 N 2 k g × 1 0 m / s 2 = 2 0 k g ⋅ m / s 2 = 2 0 N 40 N − 20 N = 20 N 4 0 N − 2 0 N = 2 0 N
물체가 운동하는 동안 물체의 운동 방향과 알짜힘의 방향이 같으므로 알짜힘이 한 일은 운동 에너지 증가량과 같다.
이를 식으로 세우면20 N × 5 m = 1 2 × 2 k g × v 2 , 2 0 N × 5 m = 2 1 × 2 k g × v 2 , 100 N ⋅ m = 1 k g × v 2 , 1 0 0 N ⋅ m = 1 k g × v 2 , 100 J = 1 k g × v 2 , 1 0 0 J = 1 k g × v 2 , 100 k g ⋅ m 2 / s 2 = 1 k g × v 2 , 1 0 0 k g ⋅ m 2 / s 2 = 1 k g × v 2 , 100 m 2 / s 2 = v 2 , 1 0 0 m 2 / s 2 = v 2 , v = 10 m / s v = 1 0 m / s
물체에 작용하는 비보존력이 한 일은 물체의 역학적 에너지 변화량과 같음을 활용하는 경우
물체는 높이 5 m 5 m 2 k g × 10 m / s 2 × 5 m = 100 k g ⋅ m 2 / s 2 = 100 J 2 k g × 1 0 m / s 2 × 5 m = 1 0 0 k g ⋅ m 2 / s 2 = 1 0 0 J
물체가 운동하는 동안 물체의 운동 방향과 비보존력(연직 위 방향으로 크기가 40 N 4 0 N
이를 식으로 세우면40 N × 5 m = 1 2 × 2 k g × v 2 + 100 J , 4 0 N × 5 m = 2 1 × 2 k g × v 2 + 1 0 0 J , 200 N ⋅ m = 1 k g × v 2 + 100 J , 2 0 0 N ⋅ m = 1 k g × v 2 + 1 0 0 J , 200 J = 1 k g × v 2 + 100 J , 2 0 0 J = 1 k g × v 2 + 1 0 0 J , 100 J = 1 k g × v 2 , 1 0 0 J = 1 k g × v 2 , 100 k g ⋅ m 2 / s 2 = 1 k g × v 2 , 1 0 0 k g ⋅ m 2 / s 2 = 1 k g × v 2 , 100 m 2 / s 2 = v 2 , 1 0 0 m 2 / s 2 = v 2 , v = 10 m / s v = 1 0 m / s
위에서 구한 내용을 바탕으로 위치별 물체의 운동 에너지, 중력 퍼텐셜 에너지, 역학적 에너지, 알짜힘과 비보존력이 한 일을 표기하면 아래 그림과 같다.
1번 문항 정답 및 해설 보기
정답: $3$
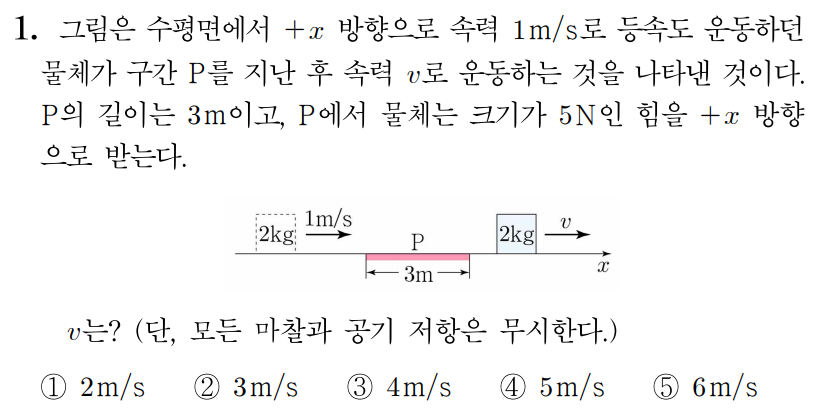
P P 5 N 5 N
이를 식으로 세우면5 N × 3 m = 1 2 × 2 k g × v 2 − 1 2 × 2 k g × ( 1 m / s ) 2 5 N × 3 m = 2 1 × 2 k g × v 2 − 2 1 × 2 k g × ( 1 m / s ) 2 15 N ⋅ m = 1 2 × 2 k g × ( v 2 − ( 1 m / s ) 2 ) , 1 5 N ⋅ m = 2 1 × 2 k g × ( v 2 − ( 1 m / s ) 2 ) , 15 J = 1 2 × 2 k g × ( v 2 − ( 1 m / s ) 2 ) , 1 5 J = 2 1 × 2 k g × ( v 2 − ( 1 m / s ) 2 ) , 15 J = 1 k g × ( v 2 − 1 m 2 / s 2 ) , 1 5 J = 1 k g × ( v 2 − 1 m 2 / s 2 ) , 15 m 2 / s 2 = v 2 − 1 m 2 / s 2 , 1 5 m 2 / s 2 = v 2 − 1 m 2 / s 2 , 16 m 2 / s 2 = v 2 , 1 6 m 2 / s 2 = v 2 , v = 4 m / s v = 4 m / s
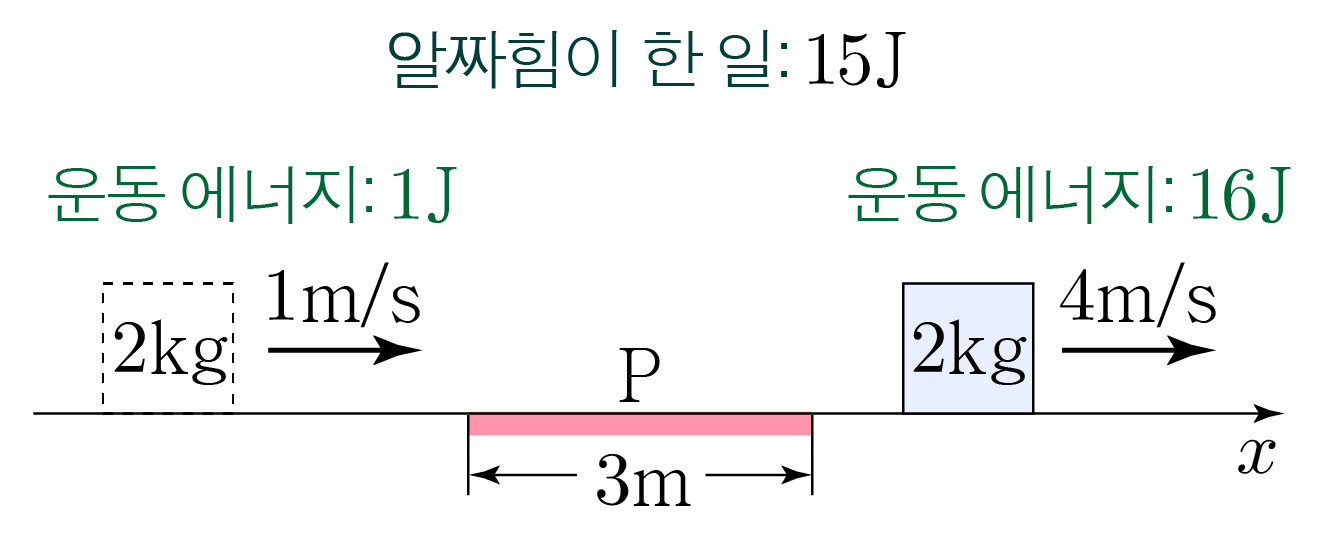
위에서 구한 내용을 바탕으로 위치별 물체의 운동 에너지, 알짜힘이 한 일을 표기하면 아래 그림과 같다.
따라서 정답은 3 3
2번 문항 정답 및 해설 보기
정답: $4$
물체에 작용하는 알짜힘이 한 일은 물체의 운동 에너지 변화량과 같음을 활용하는 경우
물체에 연직 아래 방향으로 크기가 1 k g × 10 m / s 2 = 10 k g ⋅ m / s 2 = 10 N 1 k g × 1 0 m / s 2 = 1 0 k g ⋅ m / s 2 = 1 0 N F − 10 N F − 1 0 N
물체가 운동하는 동안 물체의 운동 방향과 알짜힘의 방향이 같으므로 알짜힘이 한 일은 물체의 운동 에너지 증가량과 같다.
이를 식으로 세우면( F − 10 N ) × 2 m = 1 2 × 1 k g × ( 4 m / s ) 2 , ( F − 1 0 N ) × 2 m = 2 1 × 1 k g × ( 4 m / s ) 2 , ( F − 10 N ) × 2 m = 1 2 × 1 k g × 16 m 2 / s 2 , ( F − 1 0 N ) × 2 m = 2 1 × 1 k g × 1 6 m 2 / s 2 , ( F − 10 N ) × 2 m = 8 k g ⋅ m 2 / s 2 , ( F − 1 0 N ) × 2 m = 8 k g ⋅ m 2 / s 2 , F − 10 N = 4 k g ⋅ m / s 2 , F − 1 0 N = 4 k g ⋅ m / s 2 , F = 4 k g ⋅ m / s 2 + 10 N , F = 4 k g ⋅ m / s 2 + 1 0 N , F = 4 N + 10 N , F = 4 N + 1 0 N , F = 14 F = 1 4
물체에 작용하는 비보존력이 한 일은 물체의 역학적 에너지 변화량과 같음을 활용하는 경우
물체의 높이가 2 m 2 m 1 k g × 10 m / s 2 × 2 m = 20 k g ⋅ m 2 / s 2 = 20 J 1 k g × 1 0 m / s 2 × 2 m = 2 0 k g ⋅ m 2 / s 2 = 2 0 J
물체가 운동하는 동안 물체의 운동 방향과 비보존력(전동기가 물체를 당기는 힘)의 방향이 같으므로
이를 식으로 세우면F × 2 m = 1 2 × 1 k g × ( 4 m / s ) 2 + 20 J , F × 2 m = 2 1 × 1 k g × ( 4 m / s ) 2 + 2 0 J , F × 2 m = 1 2 × 1 k g × 16 m 2 / s 2 + 20 k g ⋅ m 2 / s 2 , F × 2 m = 2 1 × 1 k g × 1 6 m 2 / s 2 + 2 0 k g ⋅ m 2 / s 2 , F × 2 m = 8 k g ⋅ m 2 / s 2 + 20 k g ⋅ m 2 / s 2 , F × 2 m = 8 k g ⋅ m 2 / s 2 + 2 0 k g ⋅ m 2 / s 2 , F × 2 m = 28 k g ⋅ m 2 / s 2 , F × 2 m = 2 8 k g ⋅ m 2 / s 2 , F × 2 = 28 k g ⋅ m / s 2 , F × 2 = 2 8 k g ⋅ m / s 2 , F = 14 k g ⋅ m / s 2 , F = 1 4 k g ⋅ m / s 2 , F = 14 F = 1 4
위에서 구한 내용을 바탕으로 위치별 물체의 운동 에너지, 중력 퍼텐셜 에너지, 역학적 에너지, 알짜힘과 비보존력이 한 일을 표기하면 아래 그림과 같다.
따라서 정답은 4 4