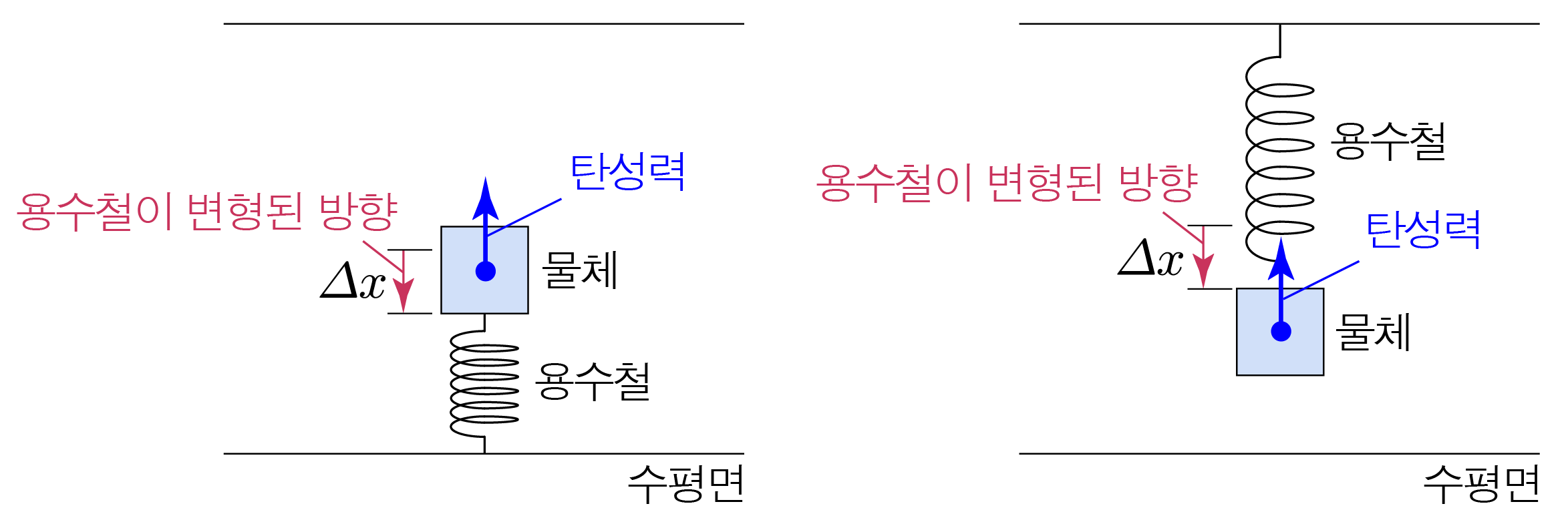
용수철의 모양을 변형시켰을 때 원래 모양으로 되돌아가려는 힘이다.
탄성력의 크기는 용수철이 변형된 길이에 비례하는데, 이 관계에서 비례 상수를 용수철 상수라고 한다.F → 탄성 F 탄성 k k Δ x Δ x Δ Δ F → 탄성 F 탄성 k Δ x k Δ x
용수철 상수 k k N / m N / m
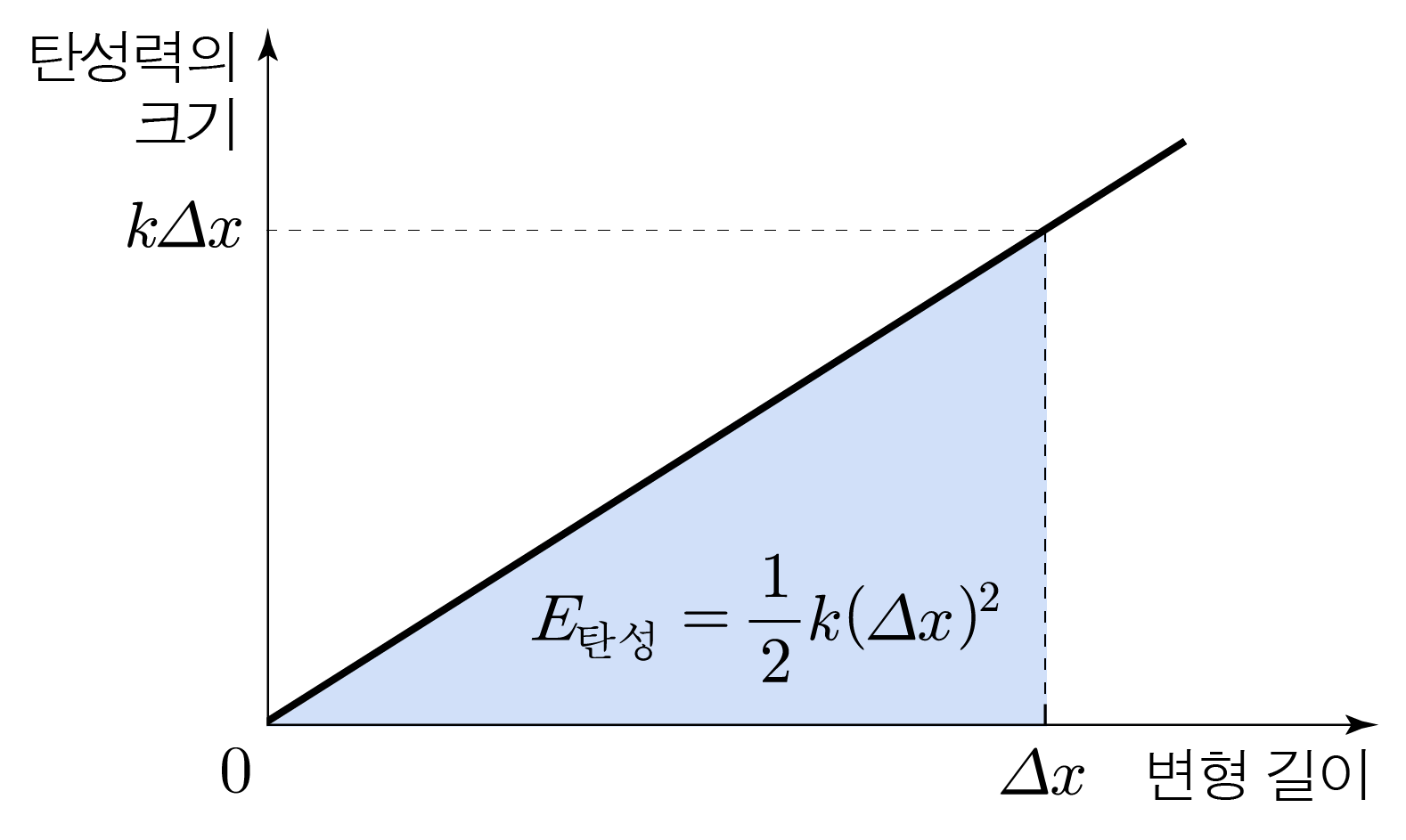
용수철이 변형되었을 때 갖는 에너지이다.E 탄성 E 탄성 k k Δ x Δ x E 탄성 = 1 2 k ( Δ x ) 2 E 탄성 = 2 1 k ( Δ x ) 2
용수철을 당기는 동안 F → 탄성 F 탄성 k Δ x k Δ x Δ x Δ x − − E 탄성 = 1 2 k ( Δ x ) 2 E 탄성 = 2 1 k ( Δ x ) 2
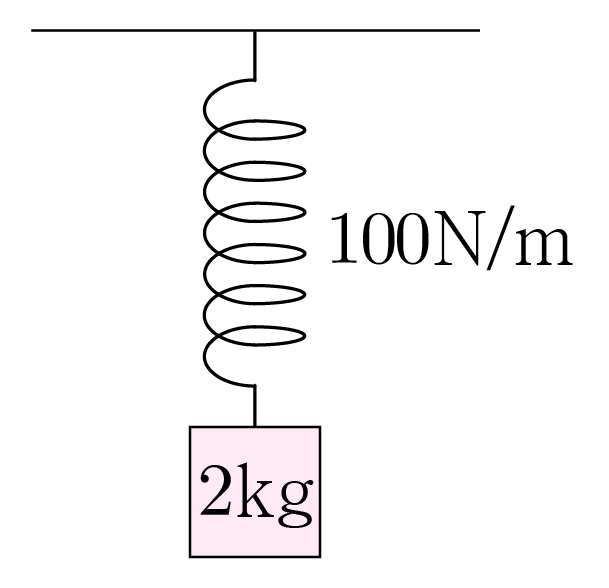
그림과 같이 질량이 2 k g 2 k g 100 N / m 1 0 0 N / m 10 m / s 2 1 0 m / s 2
물체에 작용하는 중력은 연직 아래 방향으로 크기가 2 k g × 10 m / s 2 = 20 k g ⋅ m / s 2 = 20 N 2 k g × 1 0 m / s 2 = 2 0 k g ⋅ m / s 2 = 2 0 N 0 0 20 N 2 0 N
1 1 d d F → 탄성 F 탄성 k Δ x k Δ x 20 N = 100 N / m × d , 2 0 N = 1 0 0 N / m × d , 20 N = 100 d N / m , 2 0 N = 1 0 0 d N / m , 20 m = 100 d , 2 0 m = 1 0 0 d , 20 100 m = d , 1 0 0 2 0 m = d , d = 20 100 m = 0.2 m d = 1 0 0 2 0 m = 0 . 2 m
2 2 E 탄성 = 1 2 k ( Δ x ) 2 E 탄성 = 2 1 k ( Δ x ) 2 Δ x Δ x 0.2 m 0 . 2 m E 탄성 = 1 2 × 100 N / m × ( 0.2 m ) 2 , E 탄성 = 2 1 × 1 0 0 N / m × ( 0 . 2 m ) 2 , E 탄성 = 50 N / m × ( 1 5 m ) 2 , E 탄성 = 5 0 N / m × ( 5 1 m ) 2 , E 탄성 = 50 N / m × 1 25 m 2 , E 탄성 = 5 0 N / m × 2 5 1 m 2 , E 탄성 = 2 N ⋅ m = 2 J E 탄성 = 2 N ⋅ m = 2 J
1번 문항 정답 및 해설 보기
정답: $1$
ㄱ. 물체에 작용하는 중력은 연직 아래 방향으로 크기가 2 k g × 10 m / s 2 = 20 k g ⋅ m / s 2 = 20 N 2 k g × 1 0 m / s 2 = 2 0 k g ⋅ m / s 2 = 2 0 N 0 0 20 N 2 0 N
ㄴ. F → 탄성 F 탄성 k Δ x k Δ x 20 N = 200 N / m × d , 2 0 N = 2 0 0 N / m × d , 20 N = 200 d N / m , 2 0 N = 2 0 0 d N / m , 20 m = 200 d , 2 0 m = 2 0 0 d , 20 200 m = d , 2 0 0 2 0 m = d , d = 0.1 m d = 0 . 1 m
ㄷ. E 탄성 = 1 2 k ( Δ x ) 2 = 1 2 k d 2 E 탄성 = 2 1 k ( Δ x ) 2 = 2 1 k d 2 E 탄성 = 1 2 × 200 N / m × ( 0.1 m ) 2 , E 탄성 = 2 1 × 2 0 0 N / m × ( 0 . 1 m ) 2 , E 탄성 = 100 N / m × ( 1 10 m ) 2 , E 탄성 = 1 0 0 N / m × ( 1 0 1 m ) 2 , E 탄성 = 100 N / m × 1 100 m 2 , E 탄성 = 1 0 0 N / m × 1 0 0 1 m 2 , E 탄성 = 1 N ⋅ m = 1 J E 탄성 = 1 N ⋅ m = 1 J
따라서 정답은 1 1
2번 문항 정답 및 해설 보기
정답: $3$
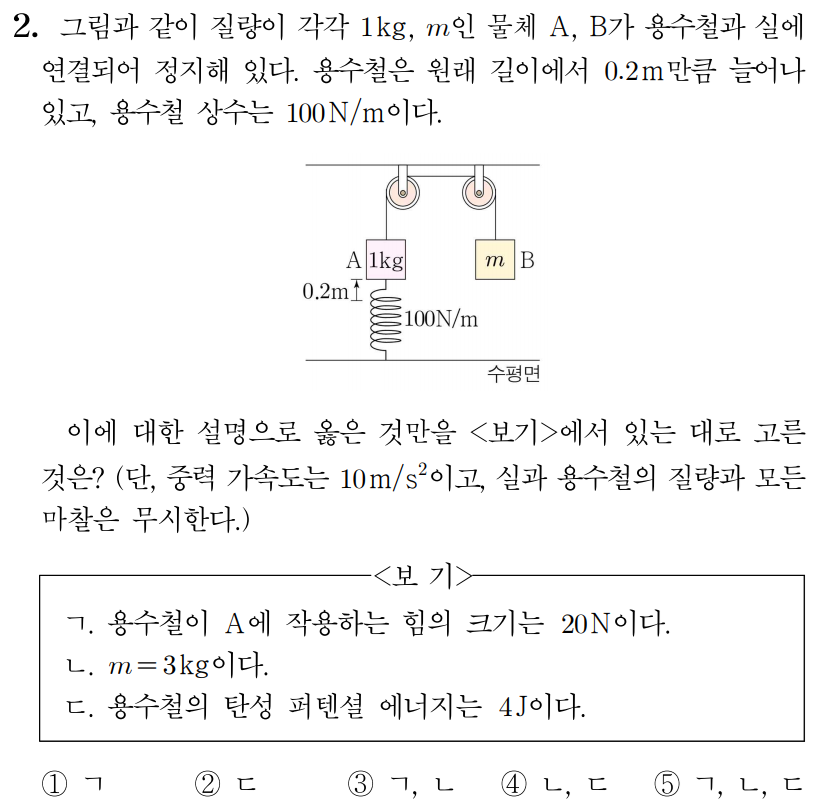
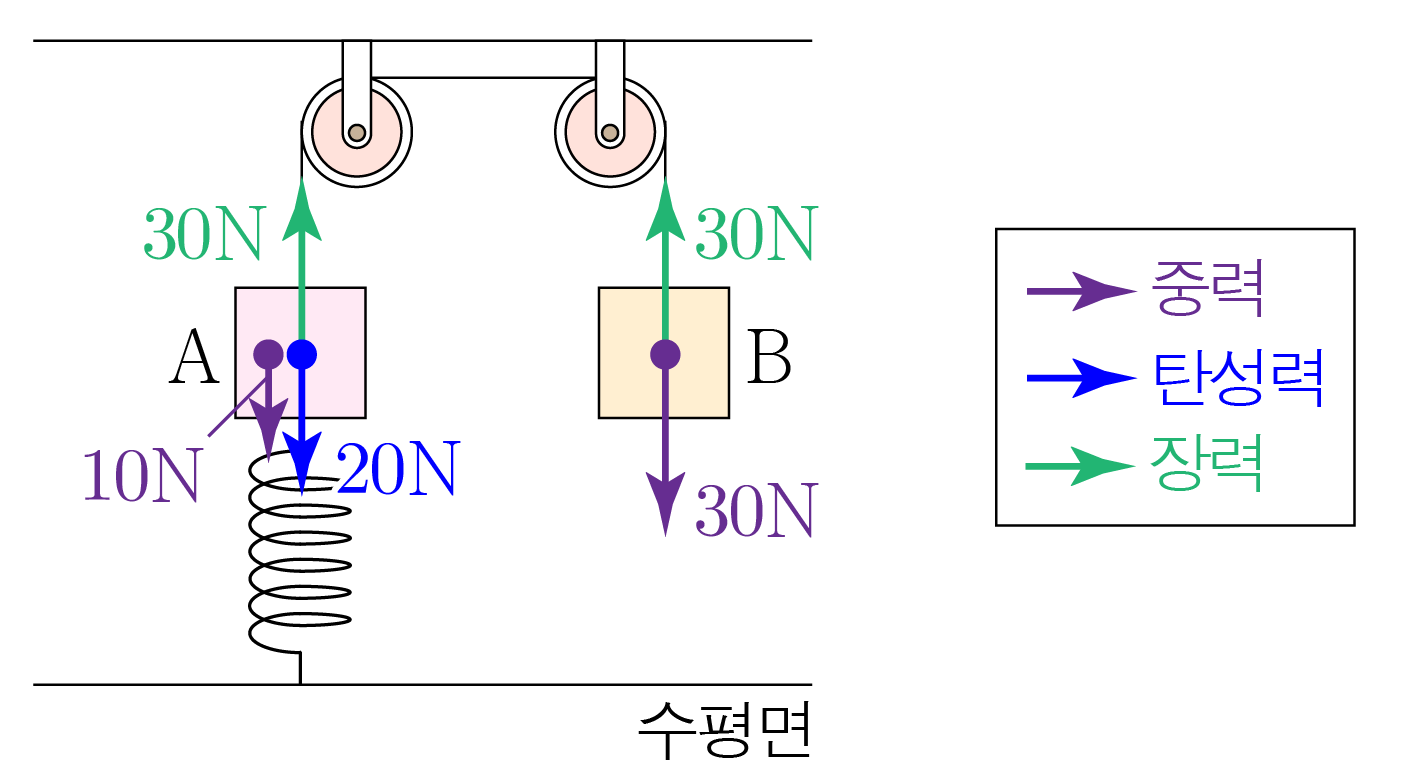
ㄱ. 용수철은 원래 길이에서 0.2 m 0 . 2 m A A A A k Δ x k Δ x 100 N / m × 0.2 m = 20 N 1 0 0 N / m × 0 . 2 m = 2 0 N
ㄴ. A A 1 k g × 10 m / s 2 = 10 k g ⋅ m / s 2 = 10 N 1 k g × 1 0 m / s 2 = 1 0 k g ⋅ m / s 2 = 1 0 N A A 10 N 1 0 N 20 N 2 0 N A A 0 0 A A 10 N + 20 N = 30 N 1 0 N + 2 0 N = 3 0 N
이때 실이 A A B B B B B B m = 30 N 10 m / s 2 = 30 k g ⋅ m / s 2 10 m / s 2 = 3 k g m = 1 0 m / s 2 3 0 N = 1 0 m / s 2 3 0 k g ⋅ m / s 2 = 3 k g
앞서 구한 내용을 바탕으로 A A B B
ㄷ. E 탄성 = 1 2 k ( Δ x ) 2 E 탄성 = 2 1 k ( Δ x ) 2 E 탄성 = 1 2 × 100 N / m × ( 0.2 m ) 2 , E 탄성 = 2 1 × 1 0 0 N / m × ( 0 . 2 m ) 2 , E 탄성 = 50 N / m × ( 1 5 m ) 2 , E 탄성 = 5 0 N / m × ( 5 1 m ) 2 , E 탄성 = 50 N / m × 1 25 m 2 , E 탄성 = 5 0 N / m × 2 5 1 m 2 , E 탄성 = 2 N ⋅ m = 2 J E 탄성 = 2 N ⋅ m = 2 J
따라서 정답은 3 3