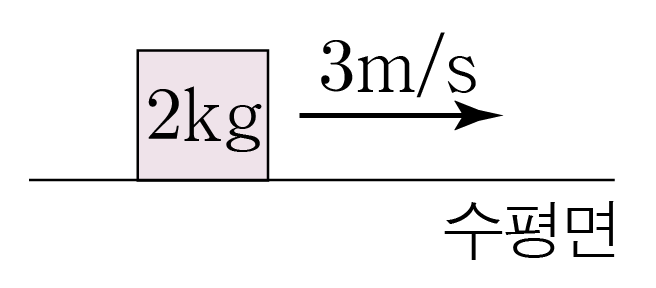물체에 작용한 힘의 크기와 힘이 작용하는 동안 물체가 이동한 거리를 곱한 값이다.− − J = N ⋅ m = k g ⋅ m 2 / s 2 J = N ⋅ m = k g ⋅ m 2 / s 2 J J J o u l e J o u l e W W
W W
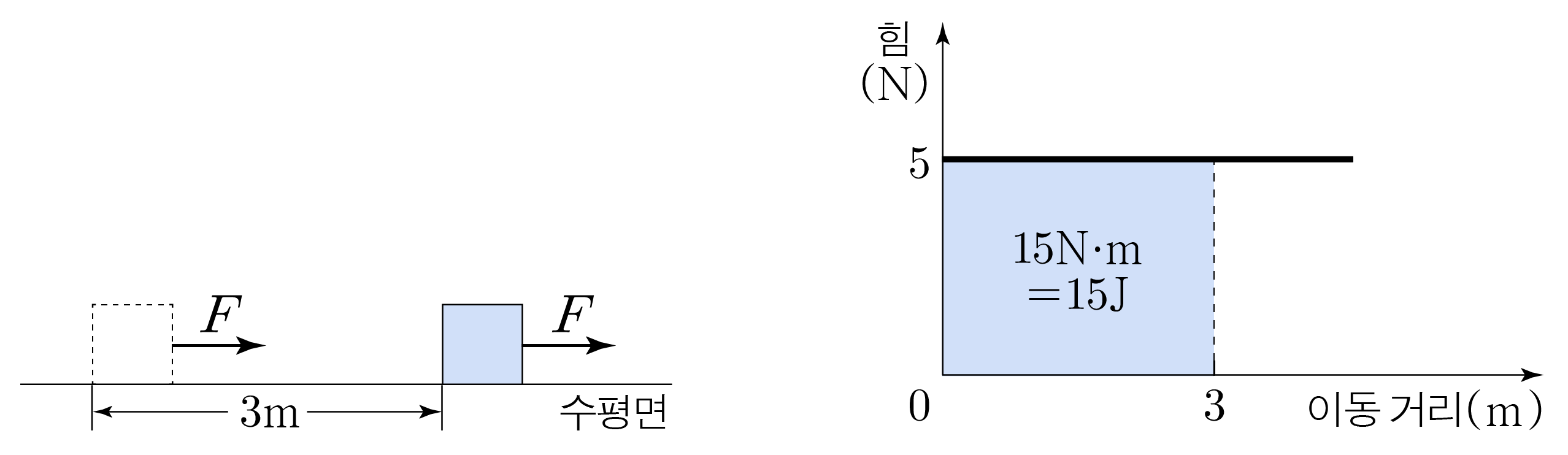
그림과 같이 어느 물체가 3 m 3 m 5 N 5 N F F F F 5 N × 3 m = 15 N ⋅ m = 15 J 5 N × 3 m = 1 5 N ⋅ m = 1 5 J
일을 할 수 있는 능력으로 기본 단위는 J J
운동하는 물체가 가지는 에너지로, 물체의 병진 운동 에너지를 E k E k m m v v E k = 1 2 m v 2 E k = 2 1 m v 2
그림과 같이 질량이 2 k g 2 k g 3 m / s 3 m / s
물체의 병진 운동 에너지를 E k E k m m v v E k = 1 2 m v 2 E k = 2 1 m v 2 E k = 1 2 × 2 k g × ( 3 m / s ) 2 = 9 k g ⋅ m 2 / s 2 = 9 J E k = 2 1 × 2 k g × ( 3 m / s ) 2 = 9 k g ⋅ m 2 / s 2 = 9 J
중력이 작용하는 공간에 있는 물체가 가지는 에너지로, 물체의 중력 퍼텐셜 에너지를 E p E p m m g g h h E p = m g h E p = m g h
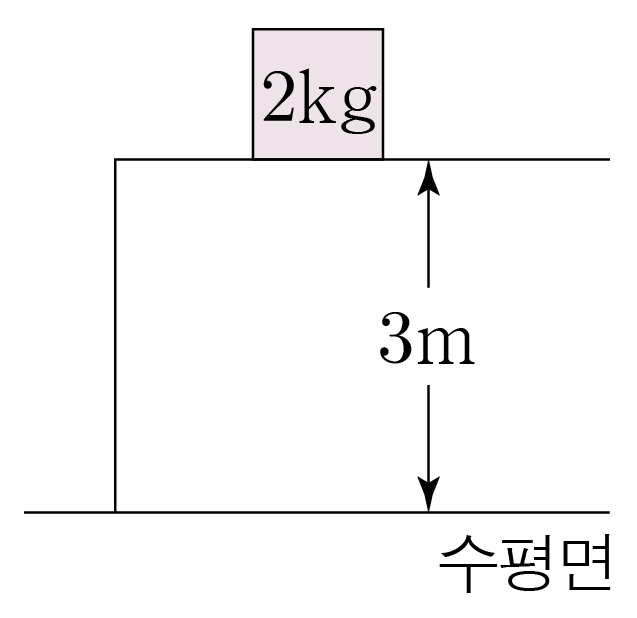
그림과 같이 질량이 2 k g 2 k g 3 m 3 m 10 m / s 2 1 0 m / s 2
물체의 중력 퍼텐셜 에너지를 E p E p m m g g h h E p = m g h E p = m g h E p = 2 k g × 10 m / s 2 × 3 m = 60 k g ⋅ m 2 / s 2 = 60 J E p = 2 k g × 1 0 m / s 2 × 3 m = 6 0 k g ⋅ m 2 / s 2 = 6 0 J
물체의 운동 에너지와 퍼텐셜 에너지의 합이다.
물체에 중력 및 수직 항력만 작용할 때, 물체의 역학적 에너지는 보존된다.
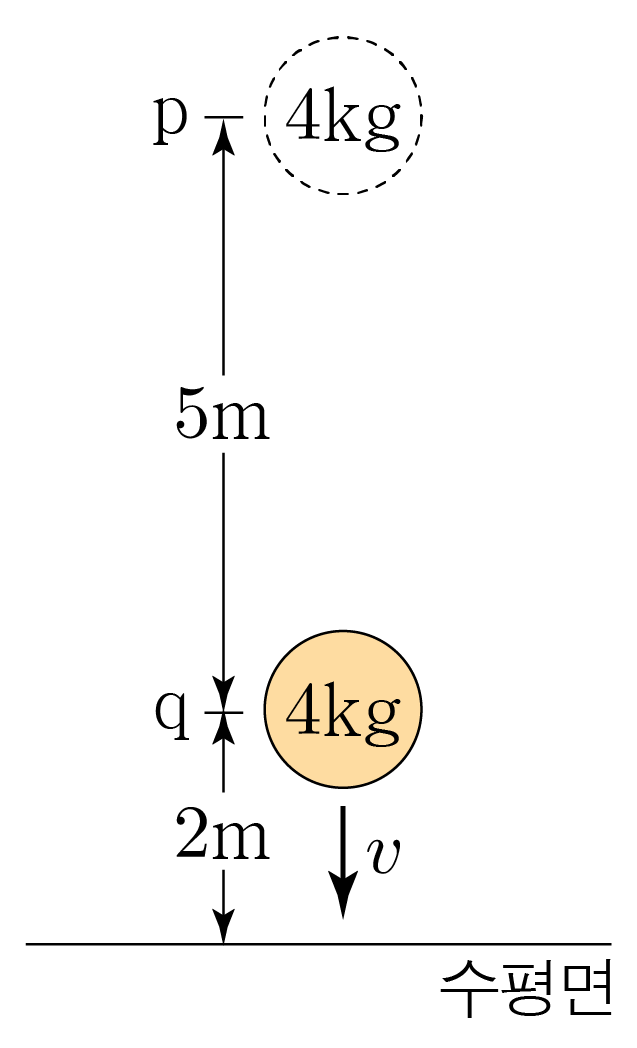
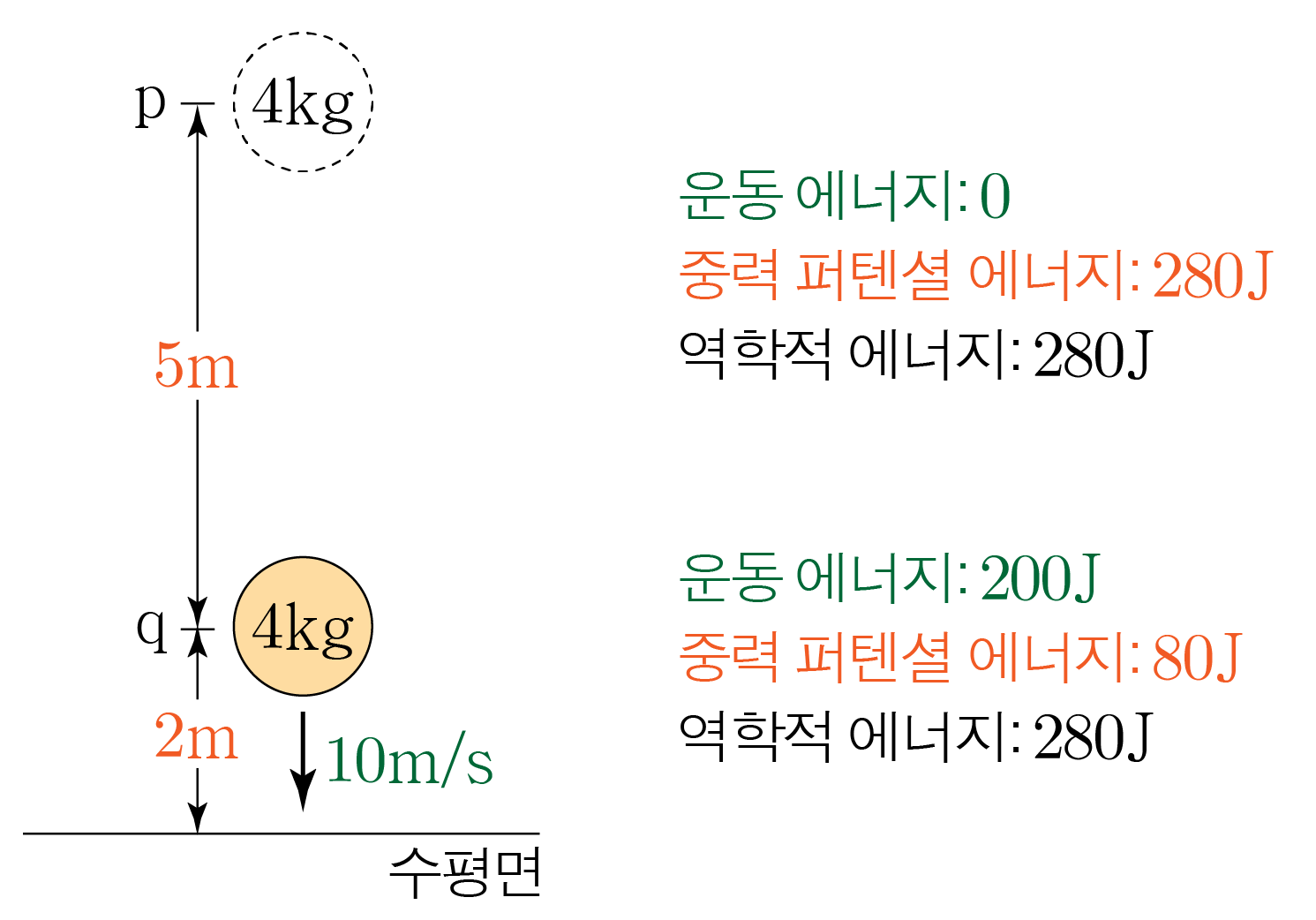
그림과 같이 질량이 4 k g 4 k g 7 m 7 m p p 2 m 2 m q q v v 10 m / s 2 1 0 m / s 2
물체가 p p q q
운동 에너지: 1 2 × 4 k g × ( 0 m / s ) 2 = 0 2 1 × 4 k g × ( 0 m / s ) 2 = 0
중력 퍼텐셜 에너지: 4 k g × 10 m / s 2 × 7 m = 280 k g ⋅ m 2 / s 2 = 280 4 k g × 1 0 m / s 2 × 7 m = 2 8 0 k g ⋅ m 2 / s 2 = 2 8 0
역학적 에너지: 0 + 280 J = 280 0 + 2 8 0 J = 2 8 0
운동 에너지: 1 2 × 4 k g × v 2 = 2 v 2 2 1 × 4 k g × v 2 = 2 v 2
중력 퍼텐셜 에너지: 4 k g × 10 m / s 2 × 2 m = 80 k g ⋅ m 2 / s 2 = 80 4 k g × 1 0 m / s 2 × 2 m = 8 0 k g ⋅ m 2 / s 2 = 8 0
역학적 에너지: 2 v 2 k g + 80 2 v 2 k g + 8 0
물체에는 중력만 작용하여 역학적 에너지는 보존된다.p p q q
280 J = 2 v 2 k g + 80 J , 2 8 0 J = 2 v 2 k g + 8 0 J , 200 J = 2 v 2 k g , 2 0 0 J = 2 v 2 k g , 100 J = 100 k g ⋅ m 2 / s 2 = v 2 k g , 1 0 0 J = 1 0 0 k g ⋅ m 2 / s 2 = v 2 k g , 100 m 2 / s 2 = v 2 , 1 0 0 m 2 / s 2 = v 2 , v = 10 m / s v = 1 0 m / s
위에서 구한 내용을 바탕으로 위치별 물체의 운동 에너지, 중력 퍼텐셜 에너지, 역학적 에너지를 표기하면 아래 그림과 같다.
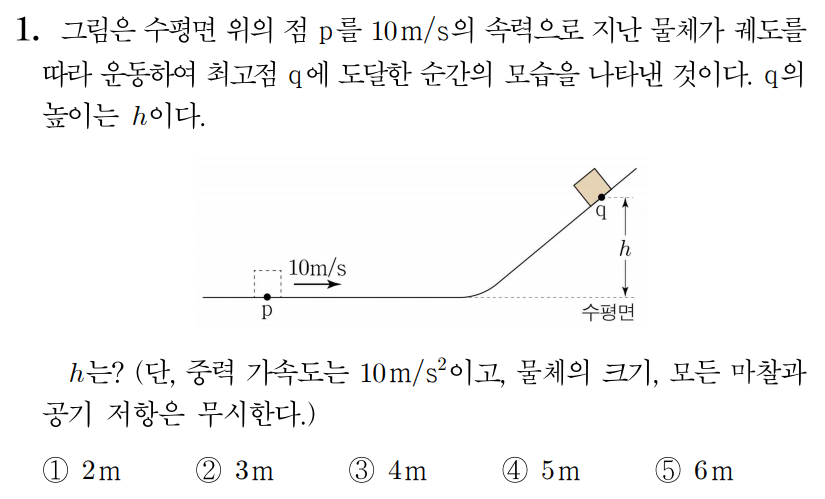
1번 문항 정답 및 해설 보기
정답: $4$
물체에 중력 및 수직 항력만 작용하므로 물체의 역학적 에너지는 보존된다.p p q q m m 1 2 m × ( 10 m / s ) 2 + m × 10 m / s 2 × 0 = 1 2 m × ( 0 ) 2 + m × 10 m / s 2 × h , 2 1 m × ( 1 0 m / s ) 2 + m × 1 0 m / s 2 × 0 = 2 1 m × ( 0 ) 2 + m × 1 0 m / s 2 × h , 1 2 m × ( 10 m / s ) 2 = m × 10 m / s 2 × h , 2 1 m × ( 1 0 m / s ) 2 = m × 1 0 m / s 2 × h , 50 m m 2 / s 2 = 10 m h m / s 2 , 5 0 m m 2 / s 2 = 1 0 m h m / s 2 , h = 5 m h = 5 m
따라서 정답은 4 4
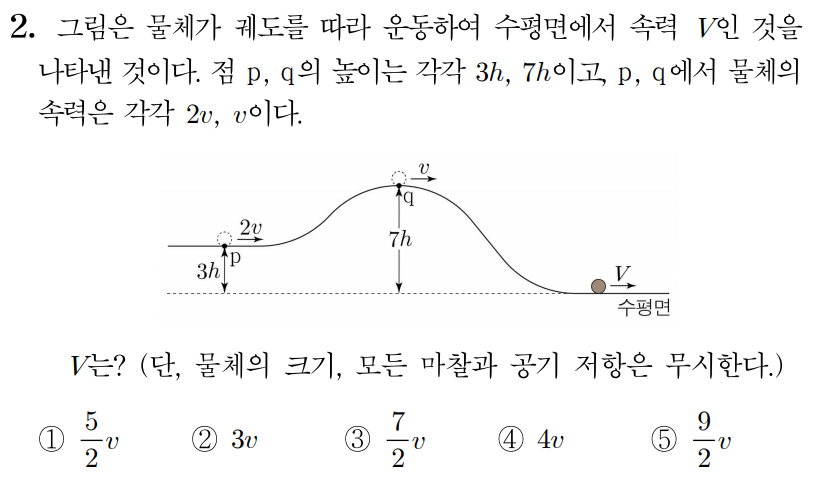
2번 문항 정답 및 해설 보기
정답: $1$
물체에 중력 및 수직 항력만 작용하므로 물체의 역학적 에너지는 보존된다.p p q q m m 1 2 m × ( 2 v ) 2 + m g × 3 h = 1 2 m × ( v ) 2 + m g × 7 h = 1 2 m × ( V ) 2 + m g × 0 , 2 1 m × ( 2 v ) 2 + m g × 3 h = 2 1 m × ( v ) 2 + m g × 7 h = 2 1 m × ( V ) 2 + m g × 0 , 2 m v 2 + 3 m g h = 1 2 m v 2 + 7 m g h = 1 2 m V 2 , 2 m v 2 + 3 m g h = 2 1 m v 2 + 7 m g h = 2 1 m V 2 , 2 v 2 + 3 g h = 1 2 v 2 + 7 g h = 1 2 V 2 2 v 2 + 3 g h = 2 1 v 2 + 7 g h = 2 1 V 2
이때 2 v 2 + 3 g h = 1 2 v 2 + 7 g h , 2 v 2 + 3 g h = 2 1 v 2 + 7 g h , 3 2 v 2 = 4 g h , 2 3 v 2 = 4 g h , g h = 3 8 v 2 g h = 8 3 v 2
이를 1 2 v 2 + 7 g h = 1 2 V 2 2 1 v 2 + 7 g h = 2 1 V 2 1 2 v 2 + 7 × 3 8 v 2 = 1 2 V 2 , 2 1 v 2 + 7 × 8 3 v 2 = 2 1 V 2 , 1 2 v 2 + 21 8 v 2 = 1 2 V 2 , 2 1 v 2 + 8 2 1 v 2 = 2 1 V 2 , 25 8 v 2 = 1 2 V 2 , 8 2 5 v 2 = 2 1 V 2 , V 2 = 25 4 v 2 , V 2 = 4 2 5 v 2 , V = 5 2 v V = 2 5 v
따라서 정답은 1 1