¶ 지식 정보
¶ 헤스의 법칙
반응물과 생성물의 종류, 상태, 양이 각각 같으면, 반응 경로에 관계없이 반응 엔탈피()의 총합은 같다.
따라서 서로 다른 두 열화학 반응식을 더하여 새로운 반응식을 만드는 것이 가능하다.
두 열화학 반응식을 더할 때는 두 반응식의 반응물, 생성물, 를 각각 더한 후,
반응물과 생성물에 종류와 상태가 같은 화합물이 있는 경우 양쪽에 같은 계수만큼 뺀다.
예를 들어, 에서 아래와 같이 가지 열화학 반응식이 있다고 해보자.
$\mathrm{A}(g) \rightarrow \mathrm{2B}(g) \qquad \Delta H^\circ = a$
$\mathrm{B}(g) \rightarrow \mathrm{C}(g) \qquad \Delta H^\circ = b$
두 열화학 반응식의 반응물, 생성물, 를 각각 더하면 아래와 같다.
- 반응물:
- 생성물:
- :
따라서 두 열화학 반응식을 더하면 다음과 같다.
반응물과 생성물에 종류와 상태가 같은 화합물인 가 있으므로 양쪽에 같은 계수인 만큼 빼주면 아래와 같다.
¶ 헤스의 법칙 예시
다음은 에서 가지 열화학 반응식이다. 이 자료로부터 를 구해보자.
$\mathrm{H_2O}(l) \rightarrow \mathrm{H_2O}(s) \qquad \Delta H^\circ = -6\,\mathrm{kJ}$⋯①
$\mathrm{H_2O}(l) \rightarrow \mathrm{H_2O}(g) \qquad \Delta H^\circ = 44\,\mathrm{kJ}$⋯②
$\mathrm{H_2O}(s) \rightarrow \mathrm{H_2O}(g) \qquad \Delta H^\circ = x\,\mathrm{kJ}$⋯③
를 구해야하므로 ①, ②를 통해 ③을 만들어야 한다.
반응물이 가 되도록 만들어야 하는데, 는 ①, ② 중 ①에서만 생성물로 있으므로 아래와 같이 ①의 역반응(④)을 구한다.
$\mathrm{H_2O}(s) \rightarrow \mathrm{H_2O}(l) \qquad \Delta H^\circ = 6\,\mathrm{kJ}$⋯④
②와 ④를 더하면
$\mathrm{H_2O}(l) + \mathrm{H_2O}(s) \rightarrow \mathrm{H_2O}(g) + \mathrm{H_2O}(l) \qquad \Delta H^\circ = 44\,\mathrm{kJ} + 6\,\mathrm{kJ}$
$\mathrm{H_2O}(s) \rightarrow \mathrm{H_2O}(g) \qquad \Delta H^\circ = 50\,\mathrm{kJ}$
이다.
따라서 이다.
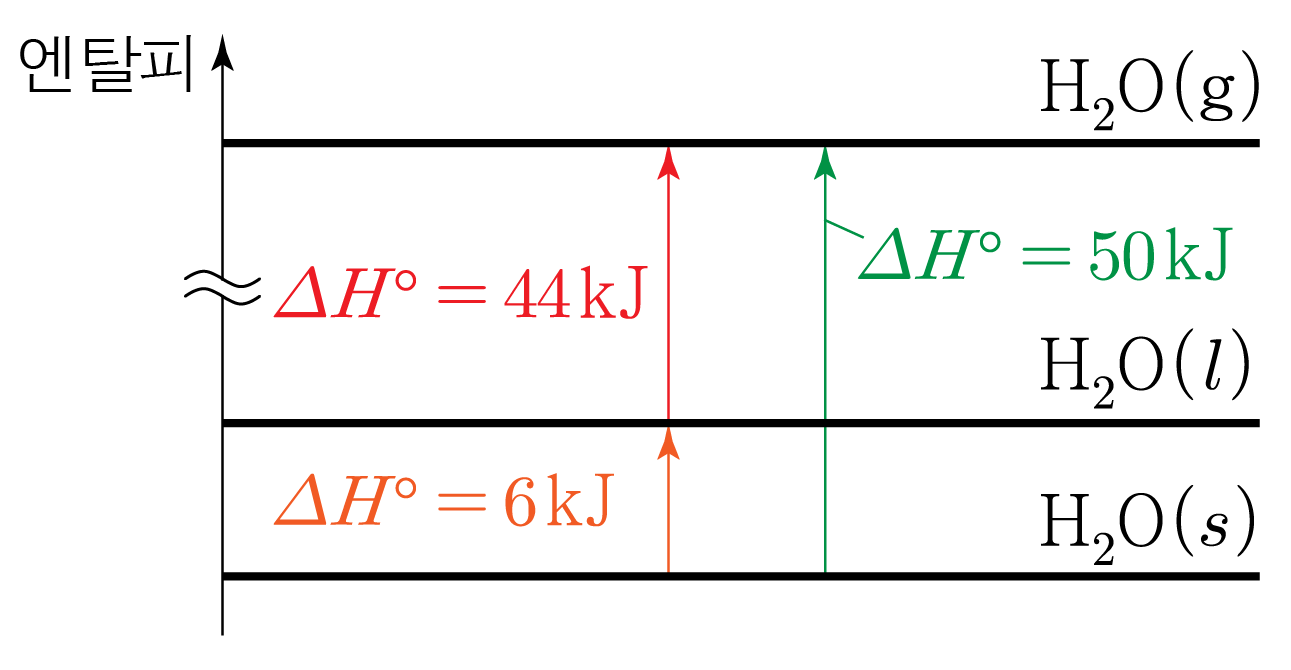
이 과정을 그림으로 나타내면 아래 그림과 같다.
¶ 적용 문항
¶ 1번 문항

정답: $3$
문제에서 주어진 열화학 반응식은 아래와 같다.
$\mathrm{N_2}(g) + \mathrm{O_2}(g) \rightarrow \mathrm{2NO}(g) \qquad \Delta H^\circ = 181\,\mathrm{kJ}$⋯①
$\mathrm{N_2}(g) + \mathrm{2O_2}(g) \rightarrow \mathrm{2NO_2}(g) \qquad \Delta H^\circ = 66\,\mathrm{kJ}$⋯②
$\mathrm{2NO}(g) + \mathrm{O_2}(g) \rightarrow \mathrm{2NO_2}(g) \qquad \Delta H^\circ = x\,\mathrm{kJ}$⋯③
를 구해야하므로 ①, ②를 통해 ③을 만들어야 한다.
반응물 중 가 포함되도록 해야하는데, 는 ①, ② 중 ①에서만 생성물로 있으므로 아래와 같이 ①의 역반응(④)을 구한다.
$\mathrm{2NO}(g) \rightarrow \mathrm{N_2}(g) + \mathrm{O_2}(g) \qquad \Delta H^\circ = -181\,\mathrm{kJ}$⋯④
②와 ④를 더하면 아래와 같다.
$\mathrm{N_2}(g) + \mathrm{2O_2}(g) + \mathrm{2NO}(g) \rightarrow \mathrm{2NO_2}(g) + \mathrm{N_2}(g) + \mathrm{O_2}(g) \qquad \Delta H^\circ = 66\,\mathrm{kJ} - 181\,\mathrm{kJ},$
$\mathrm{2O_2}(g) + \mathrm{2NO}(g) \rightarrow \mathrm{2NO_2}(g) + \mathrm{O_2}(g) \qquad \Delta H^\circ = -115\,\mathrm{kJ},$
$\mathrm{O_2}(g) + \mathrm{2NO}(g) \rightarrow \mathrm{2NO_2}(g) \qquad \Delta H^\circ = -115\,\mathrm{kJ},$
$\mathrm{2NO}(g) + \mathrm{O_2}(g) \rightarrow \mathrm{2NO_2}(g) \qquad \Delta H^\circ = -115\,\mathrm{kJ}$
그러므로 이다.
따라서 답은 번이다.
¶ 2번 문항

정답: $2$
문제에서 주어진 열화학 반응식은 아래와 같다.
$\mathrm{H_2}(g) + \mathrm{Cl_2}(g) \rightarrow \mathrm{2HCl}(g) \qquad \Delta H^\circ = -185\,\mathrm{kJ}$⋯①
$\mathrm{2H_2}(g) + \mathrm{O_2}(g) \rightarrow \mathrm{2H_2O}(l) \qquad \Delta H^\circ = -572\,\mathrm{kJ}$⋯②
$\mathrm{4HCl}(g) + \mathrm{O_2}(g) \rightarrow \mathrm{2Cl_2}(g) + \mathrm{2H_2O}(l) \qquad \Delta H^\circ = x\,\mathrm{kJ}$⋯③
를 구해야하므로 ①, ②를 통해 ③을 만들어야 한다.
반응물 중 이 포함되도록 해야하는데, 은 ①, ② 중 ①에서만 생성물로 있으므로 아래와 같이 ①의 역반응을 구한다.
③에서 의 계수가 이므로 이를 맞추기 위해 각 화합물의 계수와 에 각각 를 곱한다.
$\mathrm{4HCl}(g) \rightarrow \mathrm{2H_2}(g) + \mathrm{2Cl_2}(g) \qquad \Delta H^\circ = 370\,\mathrm{kJ}$⋯④
②와 ④를 더하면 아래와 같다.
$\mathrm{2H_2}(g) + \mathrm{O_2}(g) + \mathrm{4HCl}(g) \rightarrow \mathrm{2H_2O}(l) + \mathrm{2H_2}(g) + \mathrm{2Cl_2}(g) \qquad \Delta H^\circ = -572\,\mathrm{kJ} + 370\,\mathrm{kJ},$
$\mathrm{O_2}(g) + \mathrm{4HCl}(g) \rightarrow \mathrm{2H_2O}(l) + \mathrm{2Cl_2}(g) \qquad \Delta H^\circ = -202\,\mathrm{kJ},$
$\mathrm{4HCl}(g) + \mathrm{O_2}(g) \rightarrow \mathrm{2Cl_2}(g) + \mathrm{2H_2O}(l) \qquad \Delta H^\circ = -202\,\mathrm{kJ}$
그러므로 이다.
따라서 답은 번이다.