¶ 지식 정보
| 해당 지식 | |
|---|---|
|
|
| 하위 지식 | 상위 지식 |
|
|
¶ 쌍극자
크기가 같고 부호가 반대인 전하가 분리된 것이다.
¶ 쌍극자 모멘트
쌍극자의 전하량의 크기()와 쌍극자 사이의 거리()를 곱()한 물리량이다.
기본 단위는 이고, 기호로는 로 나타낸다.
십자 화살표()를 통해 양()의 전하에서 음()의 전하 방향으로 표시하고, 쌍극자 모멘트 방향으로 전자가 약간 몰린다.
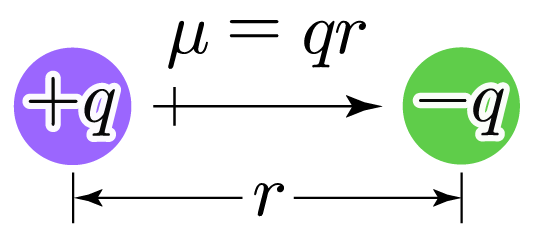
¶ 쌍극자 모멘트 예시
의 루이스 구조가 아래 그림과 같을 때, 쌍극자 모멘트를 표시해 보자.
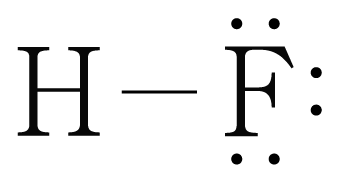
는 보다 전기 음성도가 크므로 공유 결합하고 있는 전자를 더 잘 끌어당겨 부분적인 음전하()를 띠고,
반대로 는 부분적인 양전하()를 띤다.
쌍극자 모멘트는 십자 화살표()를 통해 양()의 전하에서 음()의 전하 방향으로 표기하므로 이를 그리면 아래 그림과 같다.
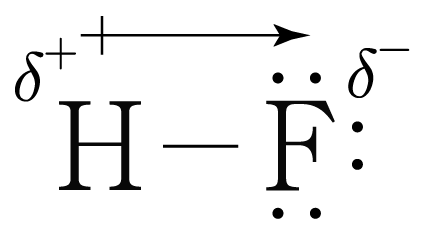
¶ 분자의 극성
분자의 쌍극자 모멘트(각 쌍극자 모멘트의 합)가 인 경우 무극성 분자, 이 아닌 경우 극성 분자이다.
¶ 분자의 극성 예시
의 극성을 판단해보자. (단, 전기 음성도 크기는 이다.)
의 극성 판단:
의 루이스 구조를 그리면 아래 그림과 같다.
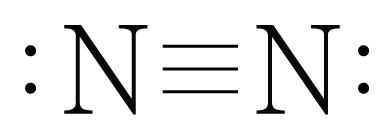
공유 결합을 하는 두 원자의 전기 음성도가 같으므로 공유 결합하고 있는 전자를 끌어당기는 능력도 같아 부분적인 전하가 생기지 않는다.
따라서 의 쌍극자 모멘트는 이고, 는 무극성 분자이다.
의 극성 판단:
의 루이스 구조를 그리면 아래 그림과 같다.
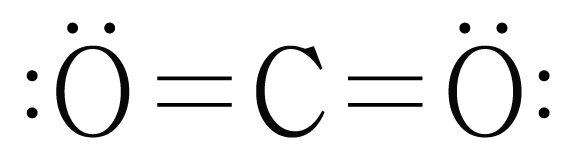
는 개와 결합하고 있으므로 결합수는 개이고, 비공유 전자쌍은 개이므로
는 직선형 구조이며, 결합각은 이다.
는 보다 전기 음성도가 크므로 공유 결합하고 있는 전자를 더 잘 끌어당겨 부분적인 음전하()를 띠고,
반대로 는 부분적인 양전하()를 띤다.
따라서 의 구조에 쌍극자 모멘트를 표기하면 아래 그림과 같다.
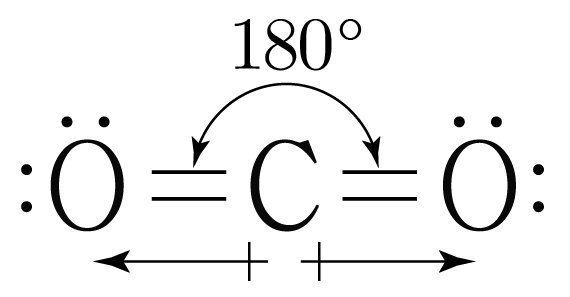
결합각이 이므로 크기가 같고 방향이 반대인 개의 쌍극자 모멘트가 완전히 상쇄되어 의 쌍극자 모멘트의 합은 이다.
그러므로 는 무극성 분자이다.
의 극성 판단:
의 루이스 구조를 그리면 아래 그림과 같다.
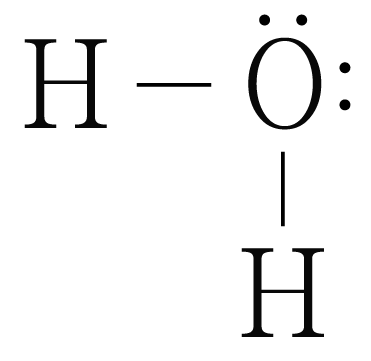
는 개와 결합하고 있으므로 결합수는 개이고, 비공유 전자쌍은 개이므로
는 굽은형 구조이며, 결합각은 약 이다.
는 보다 전기 음성도가 크므로 공유 결합하고 있는 전자를 더 잘 끌어당겨 부분적인 음전하()를 띠고,
반대로 는 부분적인 양전하()를 띤다.
따라서 의 차원 구조에 쌍극자 모멘트를 표기하면 아래 그림과 같다.
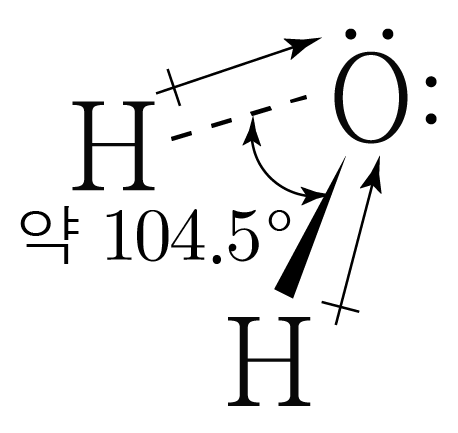
결합각이 약 이므로 개의 쌍극자 모멘트가 완전히 상쇄되지 않아 는 극성 분자이다.
의 극성 판단:
의 루이스 구조를 그리면 아래 그림과 같다.
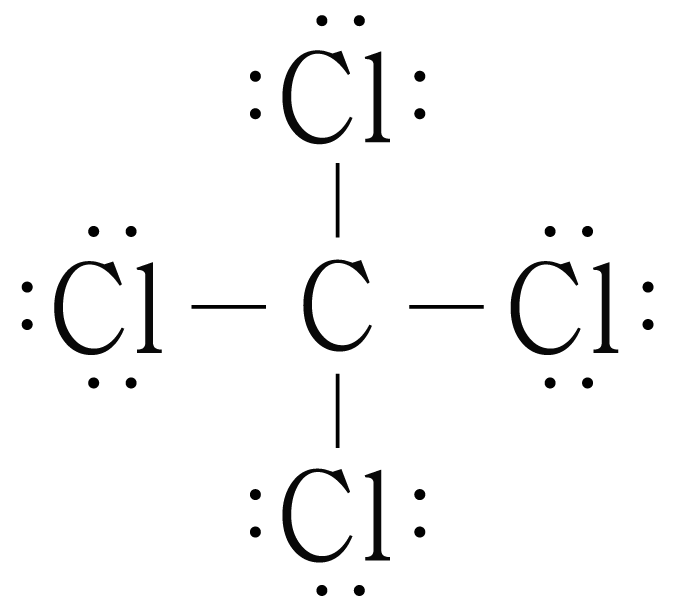
는 개와 결합하고 있으므로 결합수는 개이고, 비공유 전자쌍은 개이므로
는 사면체 구조이며, 결합각은 약 이다.
은 보다 전기 음성도가 크므로 공유 결합하고 있는 전자를 더 잘 끌어당겨 부분적인 음전하()를 띠고,
반대로 는 부분적인 양전하()를 띤다.
따라서 의 차원 구조에 쌍극자 모멘트를 표기하면 아래 그림과 같다.
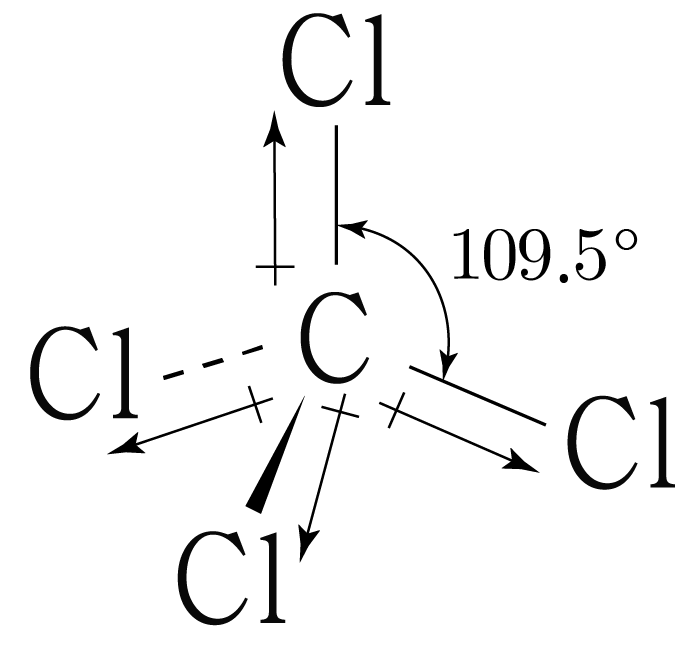
결합각이 약 이므로 개의 쌍극자 모멘트가 완전히 상쇄되어 의 쌍극자 모멘트는 이다.
그러므로 는 무극성 분자이다.
¶ 적용 문항
¶ 1번 문항
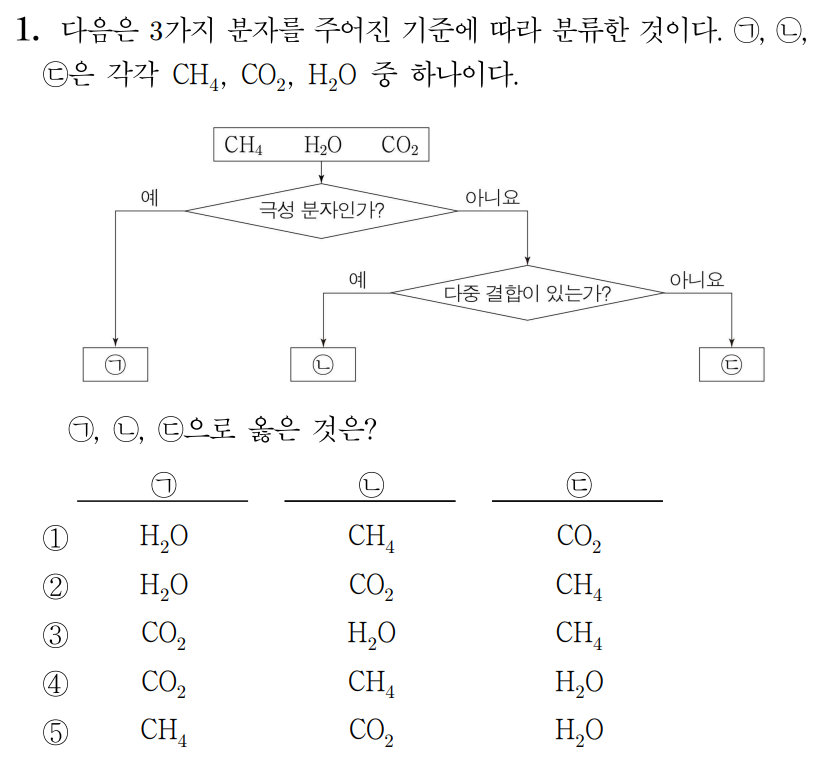
정답: $2$
의 극성을 판단해보자.
의 극성 판단:
의 루이스 구조를 그리면 아래 그림과 같다.
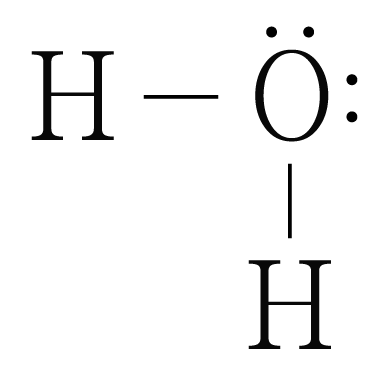
는 개와 결합하고 있으므로 결합수는 개이고, 비공유 전자쌍은 개이므로
는 굽은형 구조이며, 결합각은 약 이다.
는 보다 전기 음성도가 크므로 공유 결합하고 있는 전자를 더 잘 끌어당겨 부분적인 음전하()를 띠고,
반대로 는 부분적인 양전하()를 띤다.
따라서 의 차원 구조에 쌍극자 모멘트를 표기하면 아래 그림과 같다.
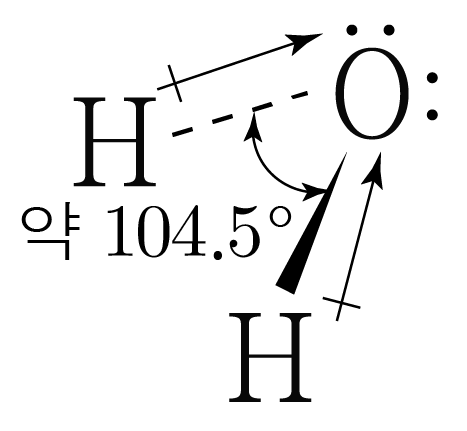
결합각이 약 이므로 개의 쌍극자 모멘트가 완전히 상쇄되지 않아 는 극성 분자이다.
의 극성 판단:
의 루이스 구조를 그리면 아래 그림과 같다.
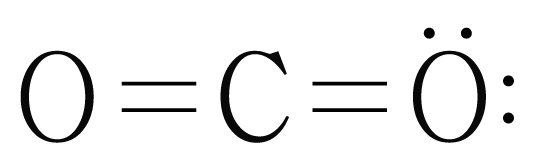
는 개와 결합하고 있으므로 결합수는 개이고, 비공유 전자쌍은 개이므로
는 직선형 구조이며, 결합각은 이다.
는 보다 전기 음성도가 크므로 공유 결합하고 있는 전자를 더 잘 끌어당겨 부분적인 음전하()를 띠고,
반대로 는 부분적인 양전하()를 띤다.
따라서 의 구조에 쌍극자 모멘트를 표기하면 아래 그림과 같다.
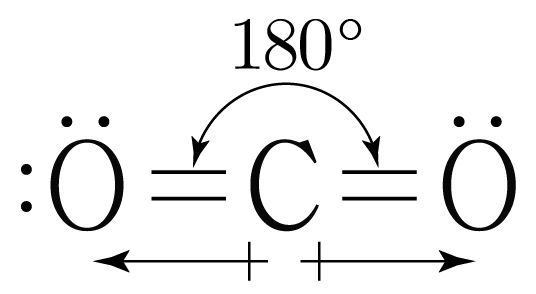
결합각이 이므로 개의 쌍극자 모멘트가 완전히 상쇄되어 의 쌍극자 모멘트의 합은 이다.
그러므로 는 무극성 분자이다.
의 극성 판단:
의 루이스 구조를 그리면 아래 그림과 같다.
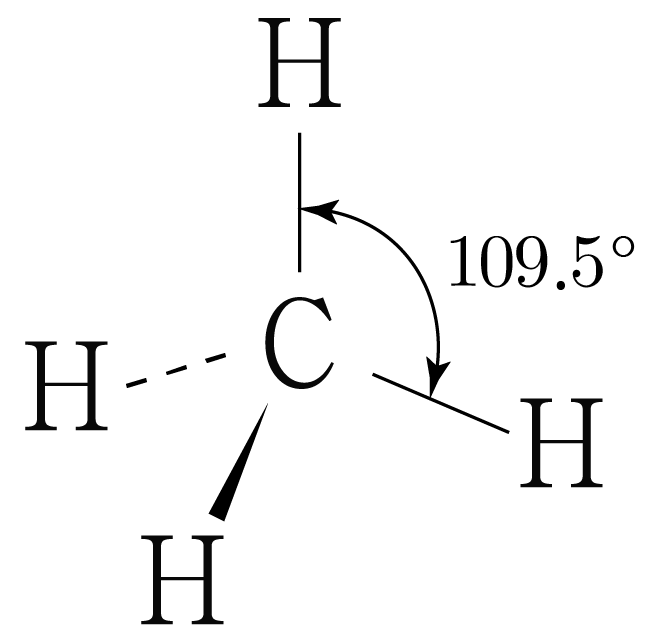
는 개와 결합하고 있으므로 결합수는 개이고, 비공유 전자쌍은 개이므로
는 사면체 구조이며, 결합각은 약 이다.
는 보다 전기 음성도가 크므로 공유 결합하고 있는 전자를 더 잘 끌어당겨 부분적인 음전하()를 띠고,
반대로 는 부분적인 양전하()를 띤다.
따라서 의 차원 구조에 쌍극자 모멘트를 표기하면 아래 그림과 같다.
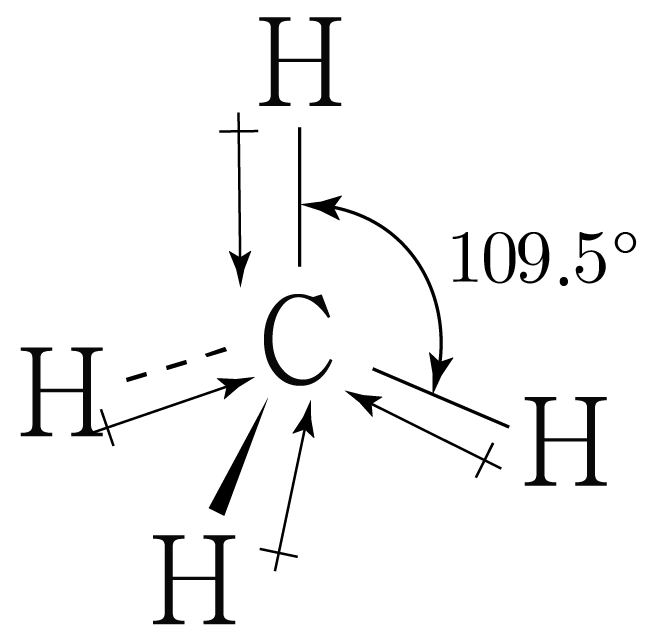
결합각이 약 이므로 개의 쌍극자 모멘트가 완전히 상쇄되어 의 쌍극자 모멘트는 이다.
그러므로 는 무극성 분자이다.
중 는 무극성 분자, 는 극성 분자이고,
중 만 다중 결합을 가지므로 ㉠, ㉡, ㉢은 각각 이다.
따라서 답은 번이다.
¶ 2번 문항
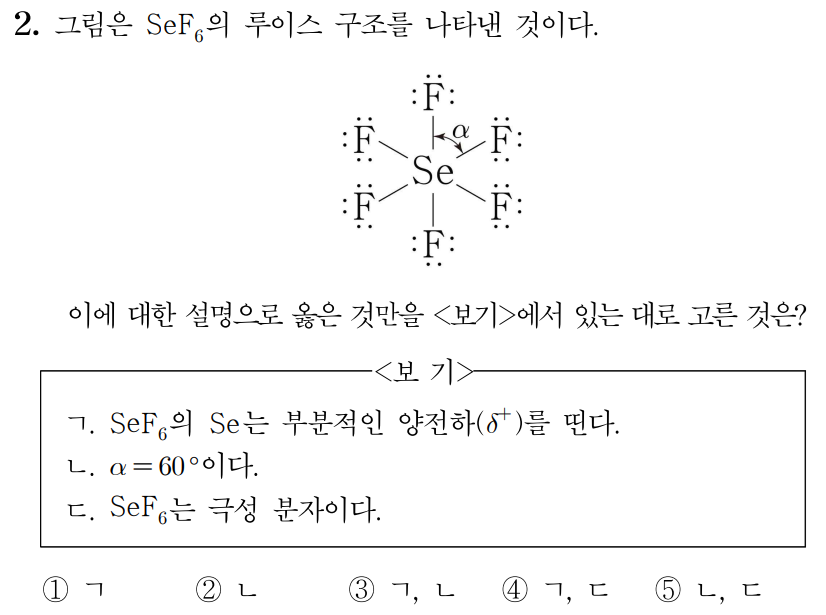
정답: $1$
는 개와 결합하고 있으므로 결합수는 개이고, 비공유 전자쌍은 개이다.
따라서 의 수평면에서 결합각은 이고,
수평면과 수직 방향의 결합각은 이며, 팔면체 구조이다.
는 보다 전기 음성도가 크므로 공유 결합하고 있는 전자를 더 잘 끌어당겨 부분적인 음전하()를 띠고,
반대로 는 부분적인 양전하()를 띤다.
따라서 의 차원 구조에 쌍극자 모멘트를 표기하면 아래 그림과 같다.
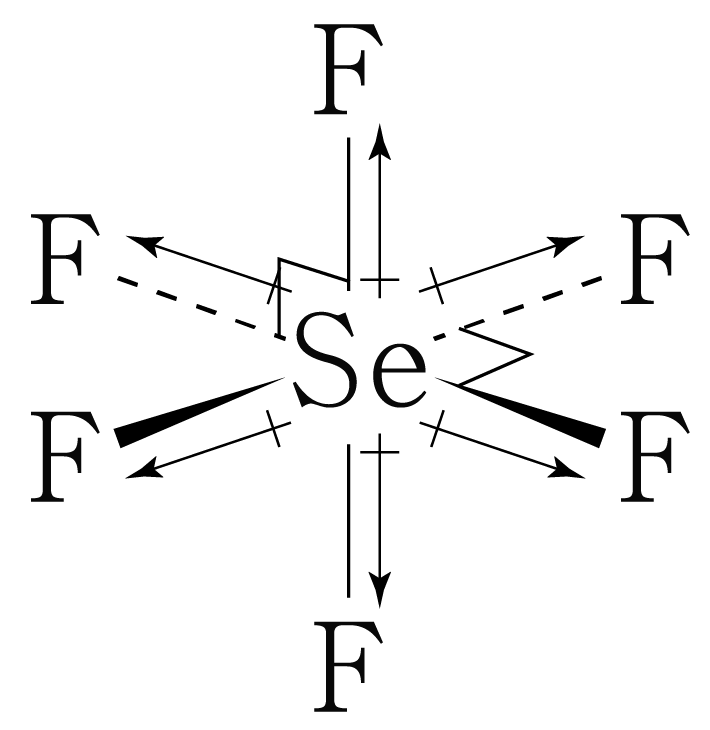
개의 쌍극자 모멘트가 완전히 상쇄되어 의 쌍극자 모멘트는 이다.
그러므로 는 무극성 분자이다.
ㄱ. 는 부분적인 양전하()를 띤다. (O)
ㄴ. 수평면에서 결합각은 이고, 수평면과 수직 방향의 결합각은 이므로 인접한 결합각은 이다.
그러므로 이다. (X)
ㄷ. 는 무극성 분자이다. (X)
따라서 답은 번이다.