정답: $2$
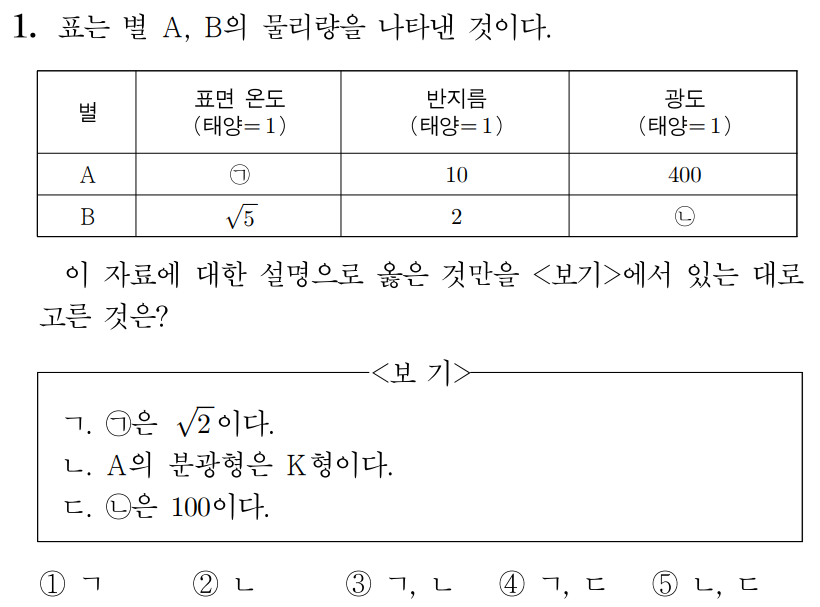
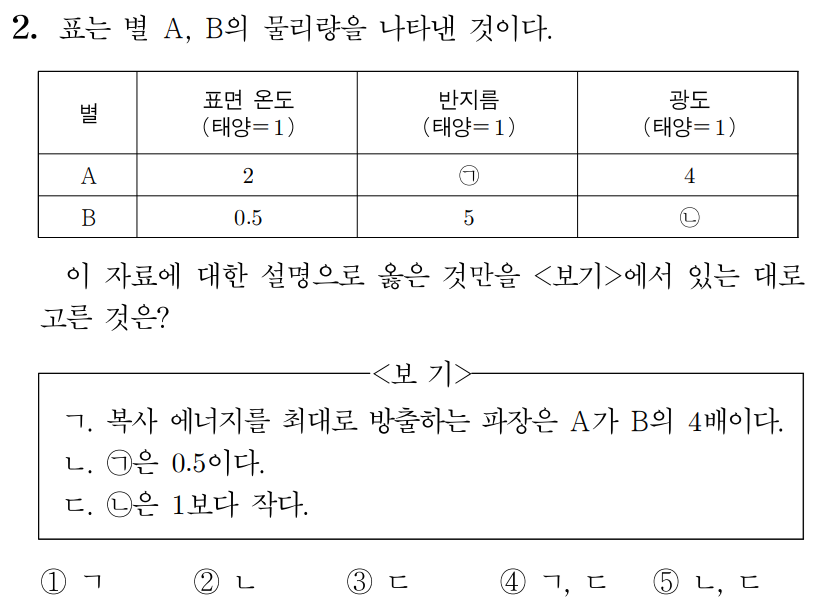
ㄱ. 빈의 변위 상수를 a, 흑체의 표면 온도를 T라 할 때, λmax=Ta이다.
태양의 표면 온도를 T⊙라 하고, A, B가 복사 에너지를 최대로 방출하는 파장을 각각 λA, λB라 할 때,
λA=2T⊙a,
λB=0.5T⊙a=0.5T⊙×10a×10=5T⊙10a=T⊙2a=2T⊙4a이다.
그러므로 복사 에너지를 최대로 방출하는 파장은 A가 B의 41배이다. (X)
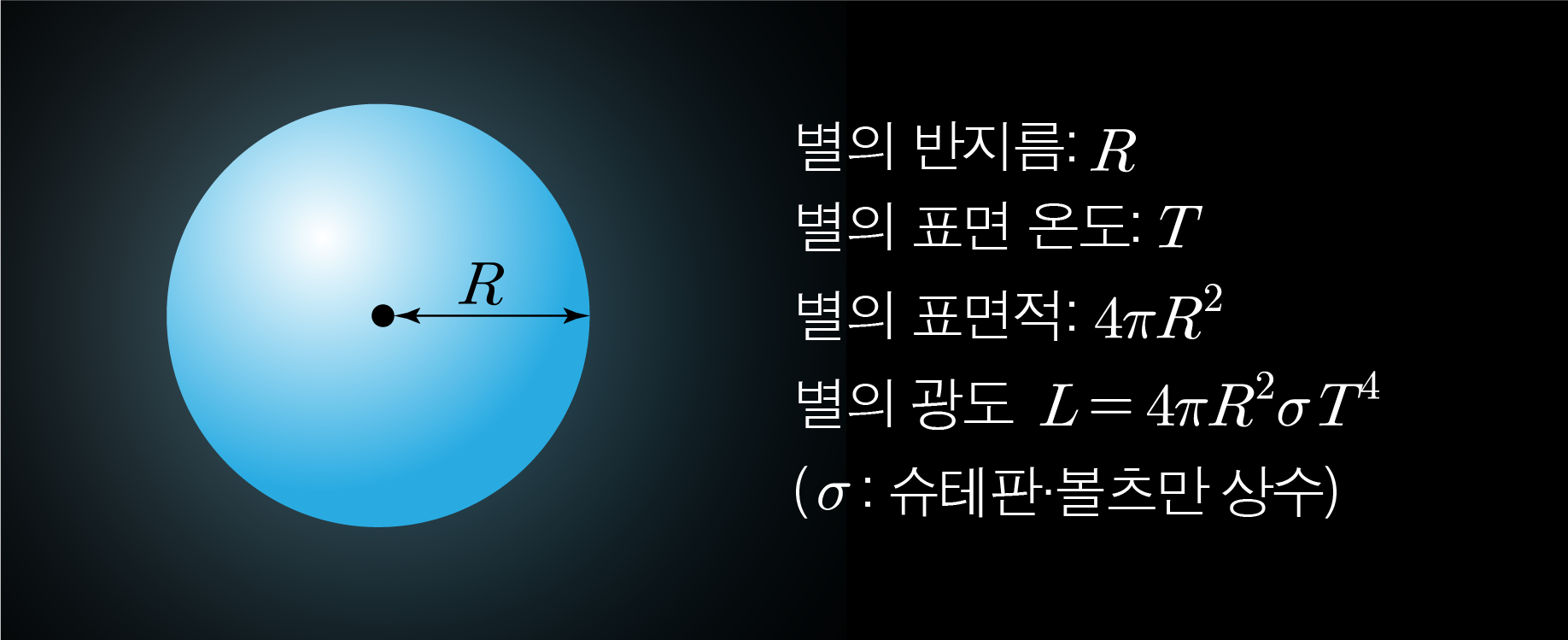
ㄴ. 슈테판·볼츠만 상수를 σ, 별의 반지름을 R, 별의 표면 온도를 T라 할 때,
광도는 L=4πR2σT4이므로 태양의 광도, 반지름을 각각 L⊙, R⊙이라 하면, L⊙=4πR⊙2σT⊙4⋯①이다.
A의 광도 4L⊙=4π(㉠R⊙)2σ(2T⊙)4이므로 L⊙에 ①을 넣으면
4×4πR⊙2σT⊙4=4π(㉠R⊙)2σ(2T⊙)4,
16πR⊙2σT⊙4=4π(㉠R⊙)2σ(2T⊙)4,
4R⊙2T⊙4=(㉠R⊙)2(2T⊙)4,
4R⊙2T⊙4=16(㉠R⊙)2T⊙4,
R⊙2=4(㉠R⊙)2,
(㉠R⊙)2=41R⊙2,
㉠R⊙=21R⊙,
㉠=21=0.5이다. (O)
ㄷ. B의 광도는 4π(5R⊙)2σ(0.5T⊙)4이므로 B의 광도를 LB라 할 때,
LB=4π(5R⊙)2σ(0.5T⊙)4,
LB=4π×25R⊙2σ(21T⊙)4,
LB=4π×25R⊙2σ×161T⊙4,
LB=16100πR⊙2σT⊙4,
LB=425πR⊙2σT⊙4이다.
①에서 L⊙=4πR⊙2σT⊙4=416πR⊙2σT⊙4이므로 LB>L⊙이다.
그러므로 ㉡은 1보다 크다. (X)
따라서 정답은 2번이다.