지구가 별빛에 의해 단위 시간(1 s 1 s 1 m 2 1 m 2 W / m 2 W / m 2
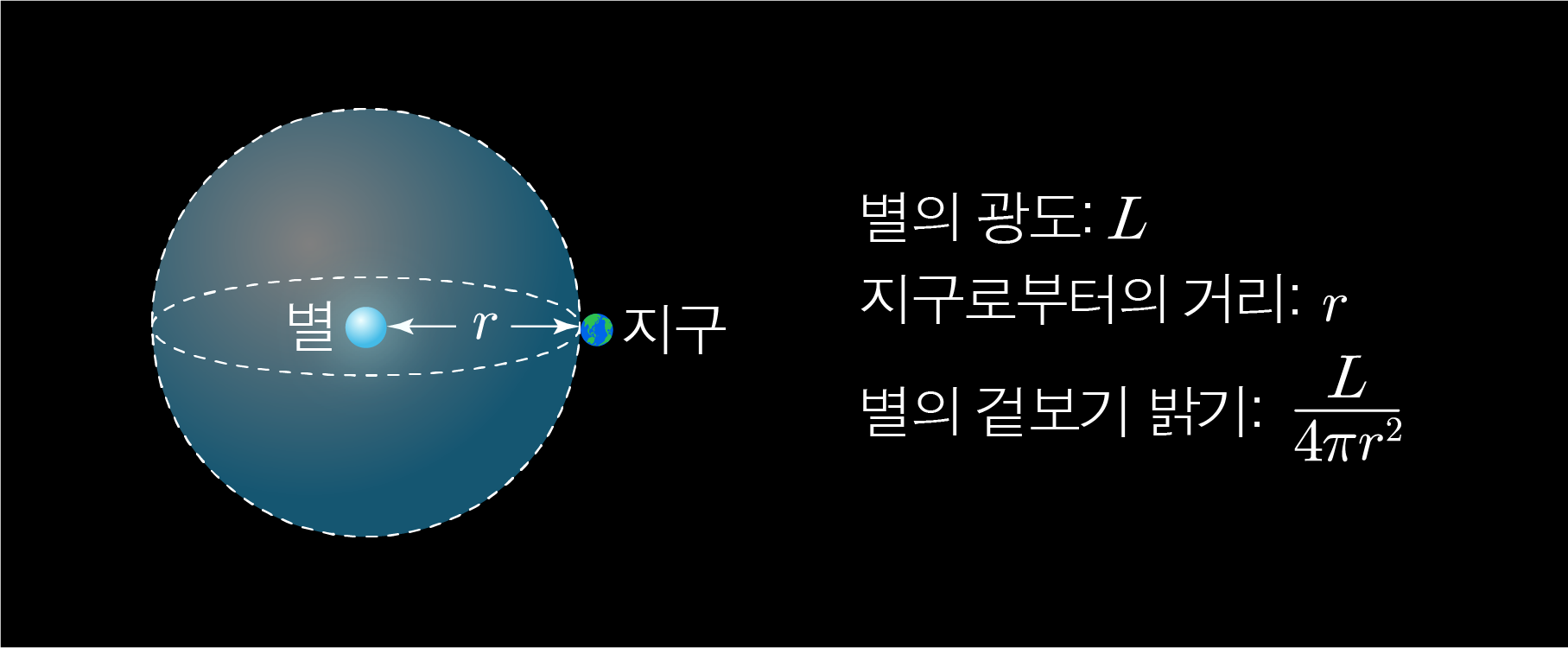
우주 공간에서 별과 행성의 크기는 상대적으로 매우 작아 하나의 점으로 볼 수 있으며,
그러므로 별의 광도를 L L r r L 4 π r 2 4 π r 2 L
표는 별 A A B B
별
광도
지구로부터의 거리
겉보기 밝기
$\mathrm{A}$
$1$
$1$
$1$
$\mathrm{B}$
$8$
$2$
$㉠$
별의 광도를 L L r r L 4 π r 2 4 π r 2 L
A A B B L L 8 L 8 L A A B B r r 2 r 2 r
A A L 4 π r 2 4 π r 2 L B B 8 L 4 π ( 2 r ) 2 = 8 L 4 π × 4 r 2 = 8 L 16 π r 2 = L 2 π r 2 4 π ( 2 r ) 2 8 L = 4 π × 4 r 2 8 L = 1 6 π r 2 8 L = 2 π r 2 L B B A A 2 2 ㉠ = 2 ㉠ = 2
매질이 없는 공간(진공)에서 빛이 약 3.26 3 . 2 6 1 p c 1 p c
밝기 1 0 2 5 1 0 5 2 1 1 별의 밝기가 클수록 등급이 낮으며, 기본 단위는 없다.
1 1 1 0 2 5 1 0 5 2 2.5 2 . 5 5 5 ( 1 0 2 5 ) 5 = 1 0 2 = 100 ( 1 0 5 2 ) 5 = 1 0 2 = 1 0 0
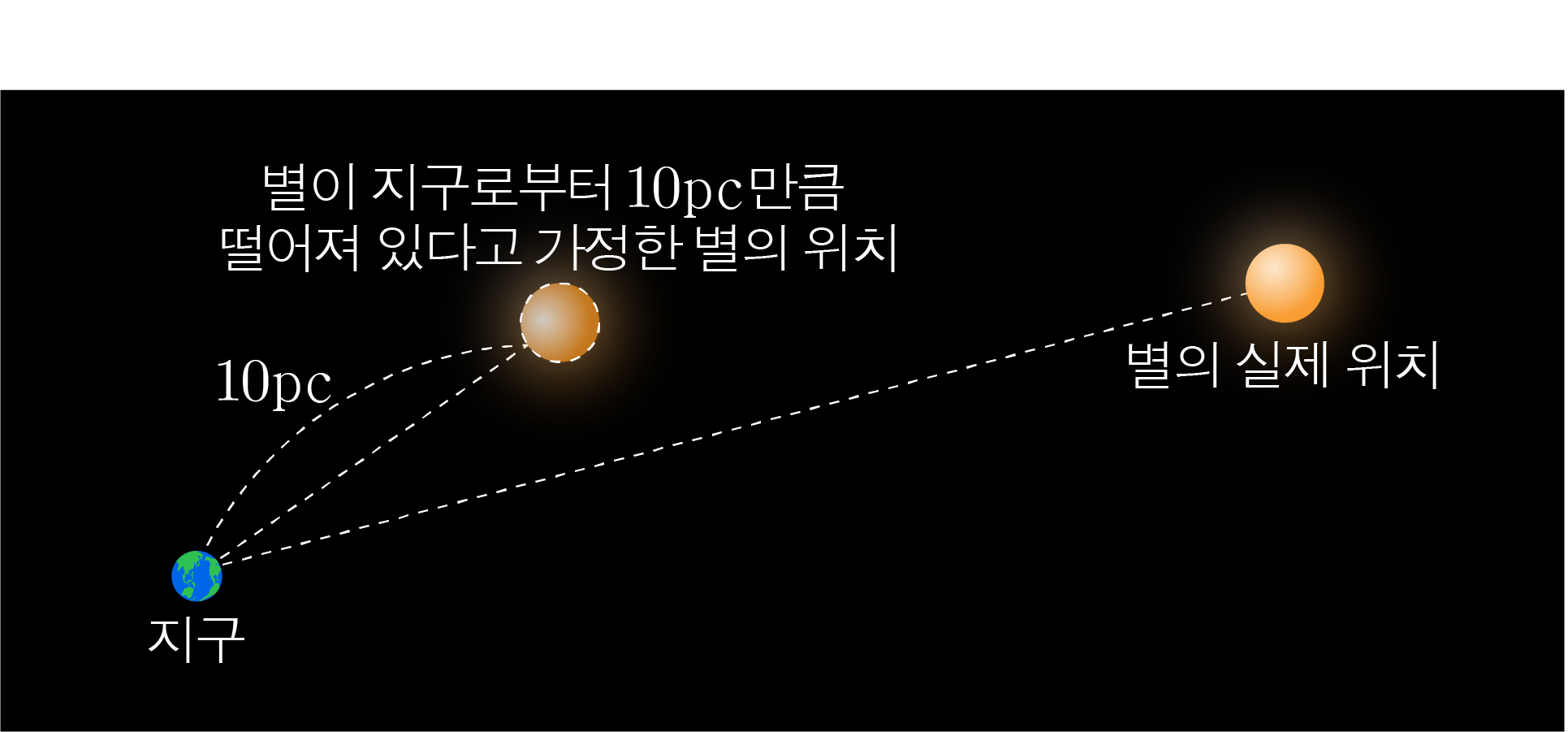
별이 지구로부터 10 p c 1 0 p c + 4.8 + 4 . 8
별의 실제 겉보기 밝기를 등급으로 바꾼 값이다. 태양의 겉보기 등급은 약 − 26.7 − 2 6 . 7
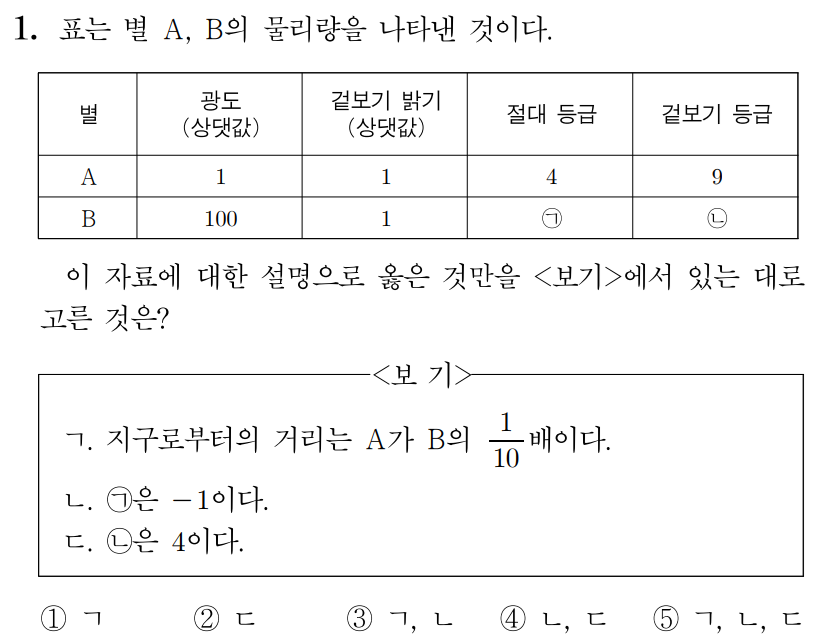
표는 별 A A B B
별
광도
절대 등급
겉보기 등급
지구로부터의
$\mathrm{A}$
$1$
$+4.8$
$㉠$
$10$
$\mathrm{B}$
$100$
$㉡$
$+4.8$
$㉢$
절대 등급은 별이 지구로부터 10 p c 1 0 p c
이때 별 A A 10 p c 1 0 p c ㉠ = + 4.8 ㉠ = + 4 . 8
별의 광도를 L L r r L 4 π r 2 4 π r 2 L
광도(L L B B A A 100 1 0 0 A A B B 10 p c 1 0 p c B B A A 100 1 0 0
별의 밝기가 클수록 등급이 낮으며, 5 5 100 1 0 0 B B A A 5 5 ㉡ = + 4.8 − 5 = − 0.2 ㉡ = + 4 . 8 − 5 = − 0 . 2
B B 5 5 10 p c 1 0 p c 100 1 0 0
그러므로 L 4 π ( 10 p c ) 2 = 100 × L 4 π ( ㉢ p c ) 2 , 4 π ( 1 0 p c ) 2 L = 1 0 0 × 4 π ( ㉢ p c ) 2 L , 1 ( 10 p c ) 2 = 100 ( ㉢ p c ) 2 , ( 1 0 p c ) 2 1 = ( ㉢ p c ) 2 1 0 0 , ( ㉢ p c ) 2 = 100 ( 10 p c ) 2 , ( ㉢ p c ) 2 = 1 0 0 ( 1 0 p c ) 2 , ( ㉢ p c ) 2 = 1 0 2 ( 10 p c ) 2 , ( ㉢ p c ) 2 = 1 0 2 ( 1 0 p c ) 2 , ㉢ p c = 10 × 10 p c , ㉢ p c = 1 0 × 1 0 p c , ㉢ p c = 100 p c , ㉢ p c = 1 0 0 p c , ㉢ = 100 ㉢ = 1 0 0
1번 문항 정답 및 해설 보기
정답: $3$
ㄱ. A A B B L L 100 L 1 0 0 L A A B B r A r A r B r B A A L 4 π r A 2 4 π r A 2 L B B 100 L 4 π r B 2 4 π r B 2 1 0 0 L
A A B B L 4 π r A 2 = 100 L 4 π r B 2 , 4 π r A 2 L = 4 π r B 2 1 0 0 L , 1 r A 2 = 100 r B 2 , r A 2 1 = r B 2 1 0 0 , r B 2 = 100 r A 2 , r B 2 = 1 0 0 r A 2 , r B = 10 r A , r B = 1 0 r A , r A = 1 10 r B r A = 1 0 1 r B
ㄴ. 광도는 B B A A 100 1 0 0 A A B B 10 p c 1 0 p c B B A A 100 1 0 0
별의 밝기가 클수록 등급이 낮으며, 5 5 100 1 0 0 B B A A 5 5 ㉠ = 4 − 5 = − 1 ㉠ = 4 − 5 = − 1
ㄷ. A A 9 − 4 = 5 9 − 4 = 5 A A 10 p c 1 0 p c 100 1 0 0
그러므로 A A r A r A L 4 π ( 10 p c ) 2 = 100 L 4 π r A 2 , 4 π ( 1 0 p c ) 2 L = 4 π r A 2 1 0 0 L , 1 ( 10 p c ) 2 = 100 r A 2 , ( 1 0 p c ) 2 1 = r A 2 1 0 0 , r A 2 = 100 × ( 10 p c ) 2 , r A 2 = 1 0 0 × ( 1 0 p c ) 2 , r A 2 = 1 0 2 × ( 10 p c ) 2 , r A 2 = 1 0 2 × ( 1 0 p c ) 2 , r A = 10 × 10 p c , r A = 1 0 × 1 0 p c , r A = 100 p c r A = 1 0 0 p c
①에서 r A = 1 10 r B r A = 1 0 1 r B r A = 100 p c r A = 1 0 0 p c r B = 1000 p c r B = 1 0 0 0 p c
따라서 B B 10 p c 1 0 p c B B L B 4 π ( 10 p c ) 2 : L B 4 π ( 1000 p c ) 2 , 4 π ( 1 0 p c ) 2 L B : 4 π ( 1 0 0 0 p c ) 2 L B , 1 ( 10 p c ) 2 : 1 ( 1000 p c ) 2 , ( 1 0 p c ) 2 1 : ( 1 0 0 0 p c ) 2 1 , ( 1000 p c ) 2 : ( 10 p c ) 2 , ( 1 0 0 0 p c ) 2 : ( 1 0 p c ) 2 , 100 0 2 : 1 0 2 , 1 0 0 0 2 : 1 0 2 , 10 0 2 : 1 2 , 1 0 0 2 : 1 2 , 10 0 2 : 1 1 0 0 2 : 1
별의 밝기가 클수록 등급이 낮으며, 5 5 100 1 0 0 10 1 0 10 0 2 1 0 0 2 B B 10 1 0 − 1 = ㉡ − 10 , − 1 = ㉡ − 1 0 , − 1 + 10 = ㉡ , − 1 + 1 0 = ㉡ , ㉡ = 9 ㉡ = 9
따라서 정답은 3 3
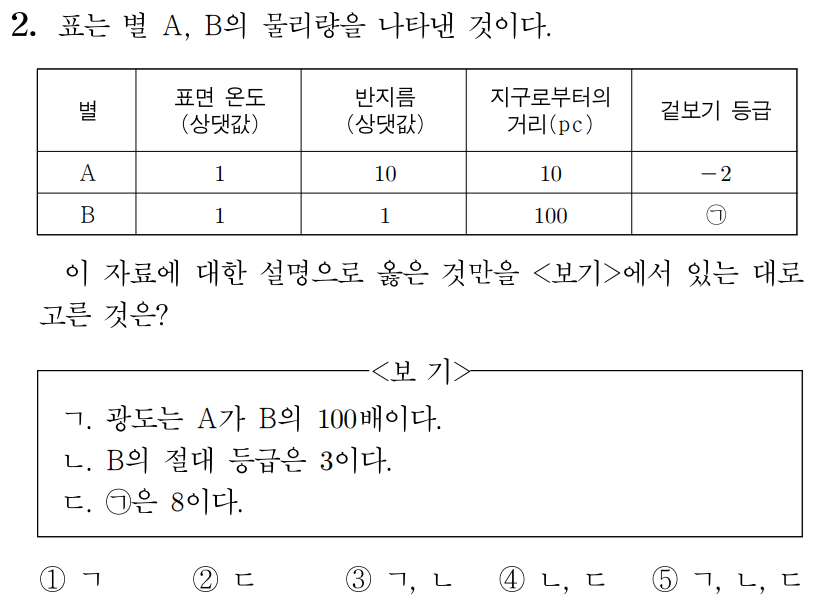
2번 문항 정답 및 해설 보기
정답: $5$
ㄱ. 슈테판-볼츠만 상수를 σ σ R R T T L = 4 π R 2 σ T 4 L = 4 π R 2 σ T 4 A A B B L A L A L B L B A A B B 10 R 1 0 R R R A A B B T T
L A = 4 π ( 10 R ) 2 σ T 4 = 4 π × 100 R 2 × σ T 4 = 400 π R 2 σ T 4 L A = 4 π ( 1 0 R ) 2 σ T 4 = 4 π × 1 0 0 R 2 × σ T 4 = 4 0 0 π R 2 σ T 4 L B = 4 π R 2 σ T 4 L B = 4 π R 2 σ T 4 L A = 100 L B L A = 1 0 0 L B
ㄴ. 절대 등급은 별이 지구로부터 10 p c 1 0 p c
이때 A A 10 p c 1 0 p c A A − 2 − 2
별의 밝기가 클수록 등급이 낮으며, 5 5 100 1 0 0 A A B B 5 5 B B M M − 2 = M − 5 , − 2 = M − 5 , M = 3 M = 3
ㄷ. B B 10 p c 1 0 p c B B L B 4 π ( 10 p c ) 2 : L B 4 π ( 100 p c ) 2 , 4 π ( 1 0 p c ) 2 L B : 4 π ( 1 0 0 p c ) 2 L B , 1 ( 10 p c ) 2 : 1 ( 100 p c ) 2 , ( 1 0 p c ) 2 1 : ( 1 0 0 p c ) 2 1 , ( 100 p c ) 2 : ( 10 p c ) 2 , ( 1 0 0 p c ) 2 : ( 1 0 p c ) 2 , 10 0 2 : 1 0 2 , 1 0 0 2 : 1 0 2 , 1 0 2 : 1 2 , 1 0 2 : 1 2 , 100 : 1 1 0 0 : 1
별의 밝기가 클수록 등급이 낮으며, 5 5 100 1 0 0 B B 5 5 3 = ㉠ − 5 , 3 = ㉠ − 5 , 3 + 5 = ㉠ , 3 + 5 = ㉠ , ㉠ = 8 ㉠ = 8
따라서 정답은 5 5