공기의 진동에 의해 전달되는 파동이다.
사람은 진동수가 약 20 ∼ 20000 H z 2 0 ∼ 2 0 0 0 0 H z
음파의 속력이다.
파동을 발생시키는 대상이다.
파원이 음파를 발생시키는 경우 해당 파원을 음원이라 한다.
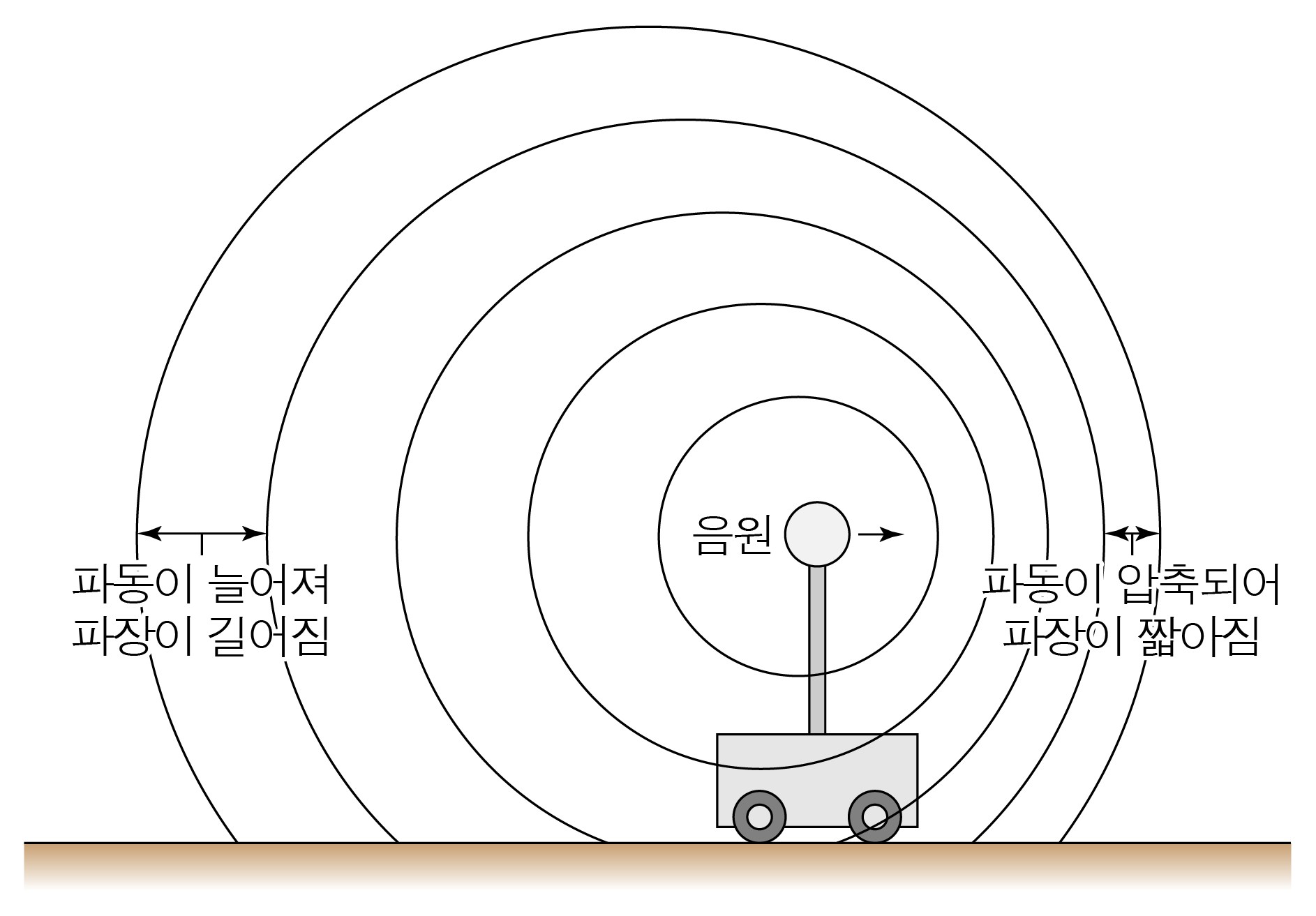
파원이나 파동을 관찰하는 관찰자가 운동할 때 파동의 진동수가 다르게 관측되는 현상이다.
음원이 관찰자와 가까워질 때 파동이 압축되어 파장이 짧아진다.v v v = f λ v = f λ f f
음원이 관찰자와 멀어질 때 파동이 늘어나 파장이 길어진다.v v v = f λ v = f λ f f
파동의 진동수를 f 0 f 0 f 1 , f 1 , V , V , v 0 , v 0 , v s v s f 1 = ( V ± v 0 V ∓ v s ) f 0 f 1 = ( V ∓ v s V ± v 0 ) f 0
± ± ∓ ∓ + + − −
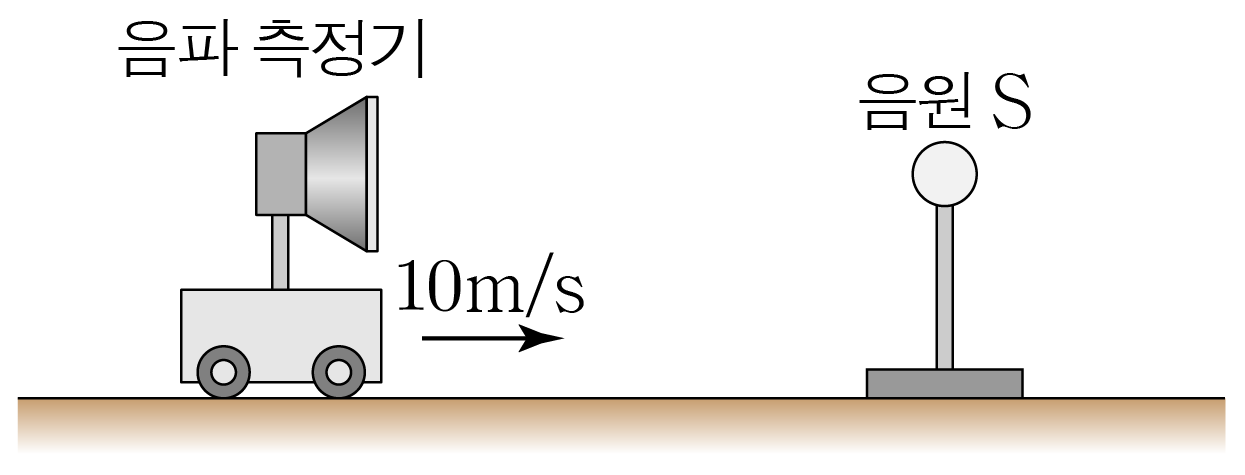
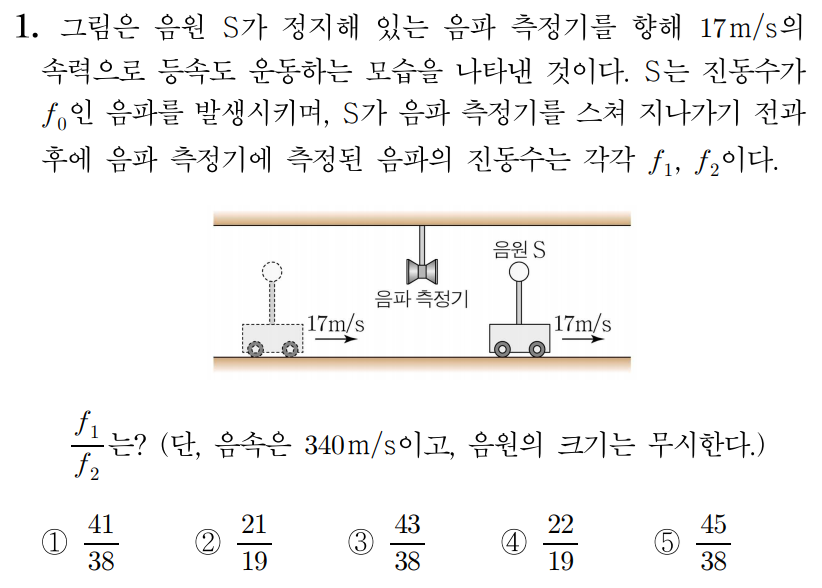
그림은 음파 측정기가 정지해 있는 음원 S S 10 m / s 1 0 m / s S S 680 H z 6 8 0 H z f f 340 m / s 3 4 0 m / s f f
파동의 진동수를 f 0 f 0 f 1 , f 1 , V , V , v 0 , v 0 , v s v s f 1 = ( V ± v 0 V ∓ v s ) f 0 f 1 = ( V ∓ v s V ± v 0 ) f 0
음원(S S v s = 0 v s = 0 S S ± ± + + − − + +
따라서 f 1 = ( V ± v 0 V ∓ v s ) f 0 f 1 = ( V ∓ v s V ± v 0 ) f 0 f = ( 340 m / s + 10 m / s 340 m / s + 0 ) × 680 H z , f = ( 3 4 0 m / s + 0 3 4 0 m / s + 1 0 m / s ) × 6 8 0 H z , f = ( 350 m / s 340 m / s ) × 680 H z , f = ( 3 4 0 m / s 3 5 0 m / s ) × 6 8 0 H z , f = 350 340 × 680 H z , f = 3 4 0 3 5 0 × 6 8 0 H z , f = 350 × 2 H z , f = 3 5 0 × 2 H z , f = 700 H z f = 7 0 0 H z
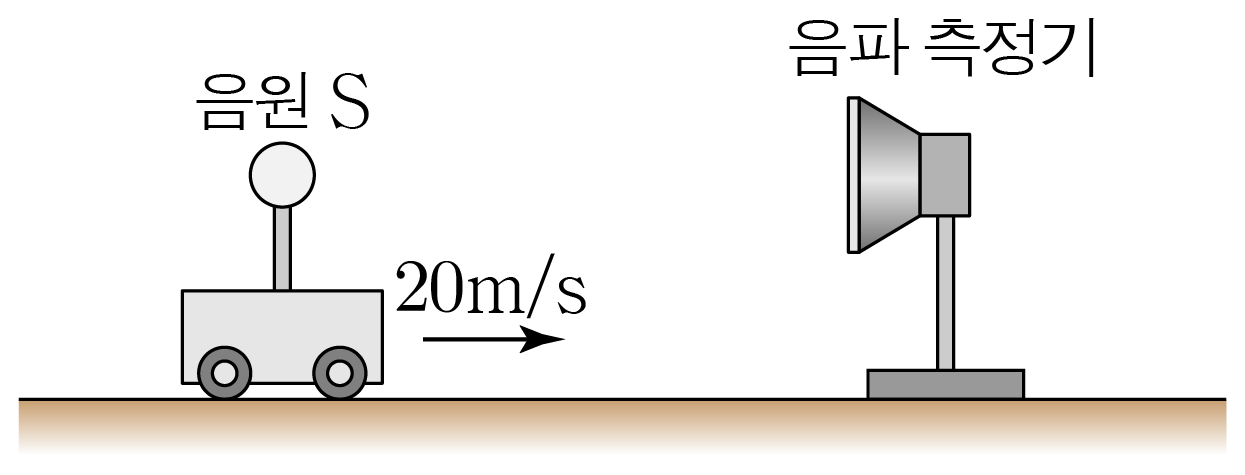
그림은 음원 S S 20 m / s 2 0 m / s S S 320 H z 3 2 0 H z f f 340 m / s 3 4 0 m / s f f
파동의 진동수를 f 0 f 0 f 1 , f 1 , V , V , v 0 , v 0 , v s v s f 1 = ( V ± v 0 V ∓ v s ) f 0 f 1 = ( V ∓ v s V ± v 0 ) f 0
관찰자(음파 측정기)는 정지해 있으므로 v 0 = 0 v 0 = 0 S S ∓ ∓ + + − − − −
따라서 f 1 = ( V ± v 0 V ∓ v s ) f 0 f 1 = ( V ∓ v s V ± v 0 ) f 0 f = ( 340 m / s + 0 340 m / s − 20 m / s ) × 320 H z , f = ( 3 4 0 m / s − 2 0 m / s 3 4 0 m / s + 0 ) × 3 2 0 H z , f = ( 340 m / s 320 m / s ) × 320 H z , f = ( 3 2 0 m / s 3 4 0 m / s ) × 3 2 0 H z , f = 340 320 × 320 H z , f = 3 2 0 3 4 0 × 3 2 0 H z , f = 340 H z f = 3 4 0 H z
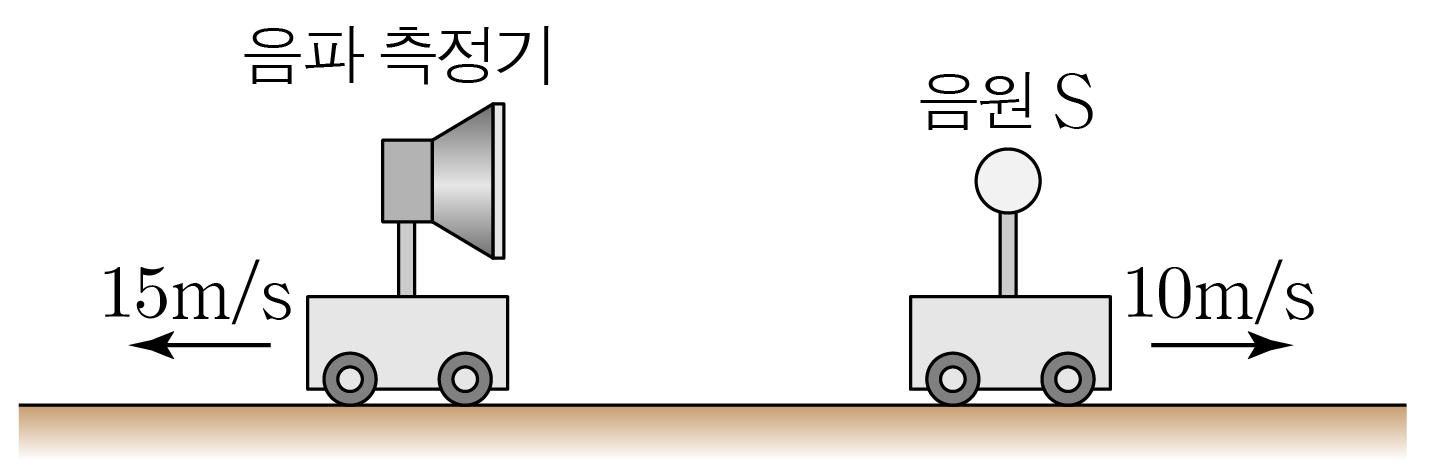
그림은 음파 측정기와 음원 S S 15 m / s , 1 5 m / s , 10 m / s 1 0 m / s S S 700 H z 7 0 0 H z f f 340 m / s 3 4 0 m / s f f
파동의 진동수를 f 0 f 0 f 1 , f 1 , V , V , v 0 , v 0 , v s v s f 1 = ( V ± v 0 V ∓ v s ) f 0 f 1 = ( V ∓ v s V ± v 0 ) f 0
관찰자(음파 측정기)가 음원(S S ± ± + + − − − −
음원(S S ∓ ∓ + + − − + +
따라서 f 1 = ( V − v 0 V + v s ) f 0 f 1 = ( V + v s V − v 0 ) f 0 f = ( 340 m / s − 15 m / s 340 m / s + 10 m / s ) × 700 H z , f = ( 3 4 0 m / s + 1 0 m / s 3 4 0 m / s − 1 5 m / s ) × 7 0 0 H z , f = ( 325 m / s 350 m / s ) × 700 H z , f = ( 3 5 0 m / s 3 2 5 m / s ) × 7 0 0 H z , f = 325 350 × 700 H z , f = 3 5 0 3 2 5 × 7 0 0 H z , f = 325 × 2 H z , f = 3 2 5 × 2 H z , f = 650 H z f = 6 5 0 H z
1번 문항 정답 및 해설 보기
정답: $2$
파동의 진동수를 f 0 f 0 f , f , V , V , v 0 , v 0 , v s v s f = ( V ± v 0 V ∓ v s ) f 0 f = ( V ∓ v s V ± v 0 ) f 0
S S v 0 = 0 v 0 = 0 S S ∓ ∓ + + − − − −
그러므로 f = ( V ± v 0 V ∓ v s ) f 0 f = ( V ∓ v s V ± v 0 ) f 0 f 1 = ( 340 m / s + 0 340 m / s − 17 m / s ) f 0 , f 1 = ( 3 4 0 m / s − 1 7 m / s 3 4 0 m / s + 0 ) f 0 , f 1 = ( 340 m / s 323 m / s ) f 0 , f 1 = ( 3 2 3 m / s 3 4 0 m / s ) f 0 , f 1 = 340 323 f 0 , f 1 = 3 2 3 3 4 0 f 0 , f 1 = 20 19 f 0 f 1 = 1 9 2 0 f 0
S S v 0 = 0 v 0 = 0 S S ∓ ∓ + + − − + +
따라서 f = ( V ± v 0 V ∓ v s ) f 0 f = ( V ∓ v s V ± v 0 ) f 0 f 2 = ( 340 m / s + 0 340 m / s + 17 m / s ) f 0 , f 2 = ( 3 4 0 m / s + 1 7 m / s 3 4 0 m / s + 0 ) f 0 , f 2 = ( 340 m / s 357 m / s ) f 0 , f 2 = ( 3 5 7 m / s 3 4 0 m / s ) f 0 , f 2 = 340 357 f 0 , f 2 = 3 5 7 3 4 0 f 0 , f 2 = 20 21 f 0 f 2 = 2 1 2 0 f 0
그러므로 f 1 f 2 = 20 19 f 0 20 21 f 0 = 20 19 20 21 = 20 19 × 21 20 = 21 19 f 2 f 1 = 2 1 2 0 f 0 1 9 2 0 f 0 = 2 1 2 0 1 9 2 0 = 1 9 2 0 × 2 0 2 1 = 1 9 2 1
따라서 정답은 2 2
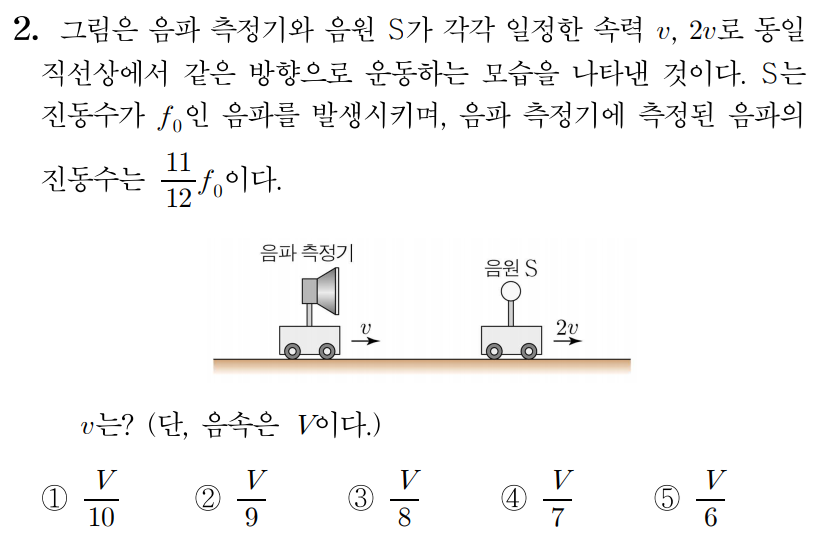
2번 문항 정답 및 해설 보기
정답: $1$
파동의 진동수를 f 0 f 0 f 1 , f 1 , V , V , v , v , 2 v 2 v f 1 = ( V ± v V ∓ 2 v ) f 0 f 1 = ( V ∓ 2 v V ± v ) f 0
관찰자(음파 측정기)가 음원(S S ± ± + + − − + +
음원(S S ∓ ∓ + + − − + +
그러므로 f 1 = ( V + v V + 2 v ) f 0 f 1 = ( V + 2 v V + v ) f 0 11 12 f 0 = ( V + v V + 2 v ) f 0 , 1 2 1 1 f 0 = ( V + 2 v V + v ) f 0 , 11 12 = V + v V + 2 v , 1 2 1 1 = V + 2 v V + v , 11 ( V + 2 v ) = 12 ( V + v ) , 1 1 ( V + 2 v ) = 1 2 ( V + v ) , 11 V + 22 v = 12 V + 12 v , 1 1 V + 2 2 v = 1 2 V + 1 2 v , 22 v = V + 12 v , 2 2 v = V + 1 2 v , 10 v = V , 1 0 v = V , v = V 10 v = 1 0 V
따라서 정답은 1 1
