¶ 지식 정보
¶ 작용·반작용 법칙
힘은 항상 쌍으로 작용하며, 두 힘의 작용점은 상호 작용하는 각각의 물체에 있고 크기는 같고 방향은 반대이다.
이때 기준이 되는 힘을 작용이라고 하며, 그 힘과 동시에 크기가 같고 방향은 반대로 작용하는 힘을 반작용이라 한다.
¶ 작용·반작용 관계에 있는 힘 파악
작용·반작용 관계에 있는 힘은 주어와 목적어만 서로 반대이다.
¶ 작용·반작용 관계에 있는 힘 파악 예시
- (주어)가 (목적어)에 작용하는 힘은 (주어)가 (목적어)에 작용하는 힘과 작용·반작용 관계에 있다.
- (주어)가 (목적어)를 미는 힘은 (주어)가 (목적어)를 미는 힘과 작용·반작용 관계에 있다.
- 지구(주어)가 물체(목적어)를 끌어당기는 힘(물체에 작용하는 중력)은 물체(주어)가 지구(목적어)를 끌어당기는 힘과 작용·반작용 관계에 있다.
¶ 작용·반작용 법칙 예시
작용·반작용 법칙의 실생활 예시:
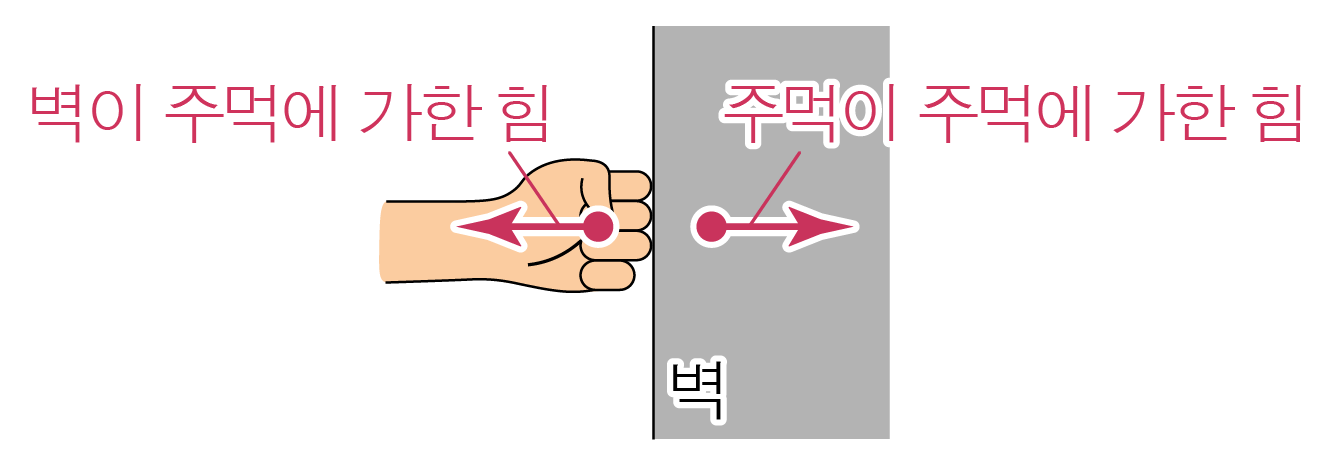
- 주먹으로 벽을 강하게 치는 경우:
주먹으로 벽에 힘을 가했지만, 그에 대한 반작용으로 벽도 주먹에 힘을 가해 주먹이 아프다.
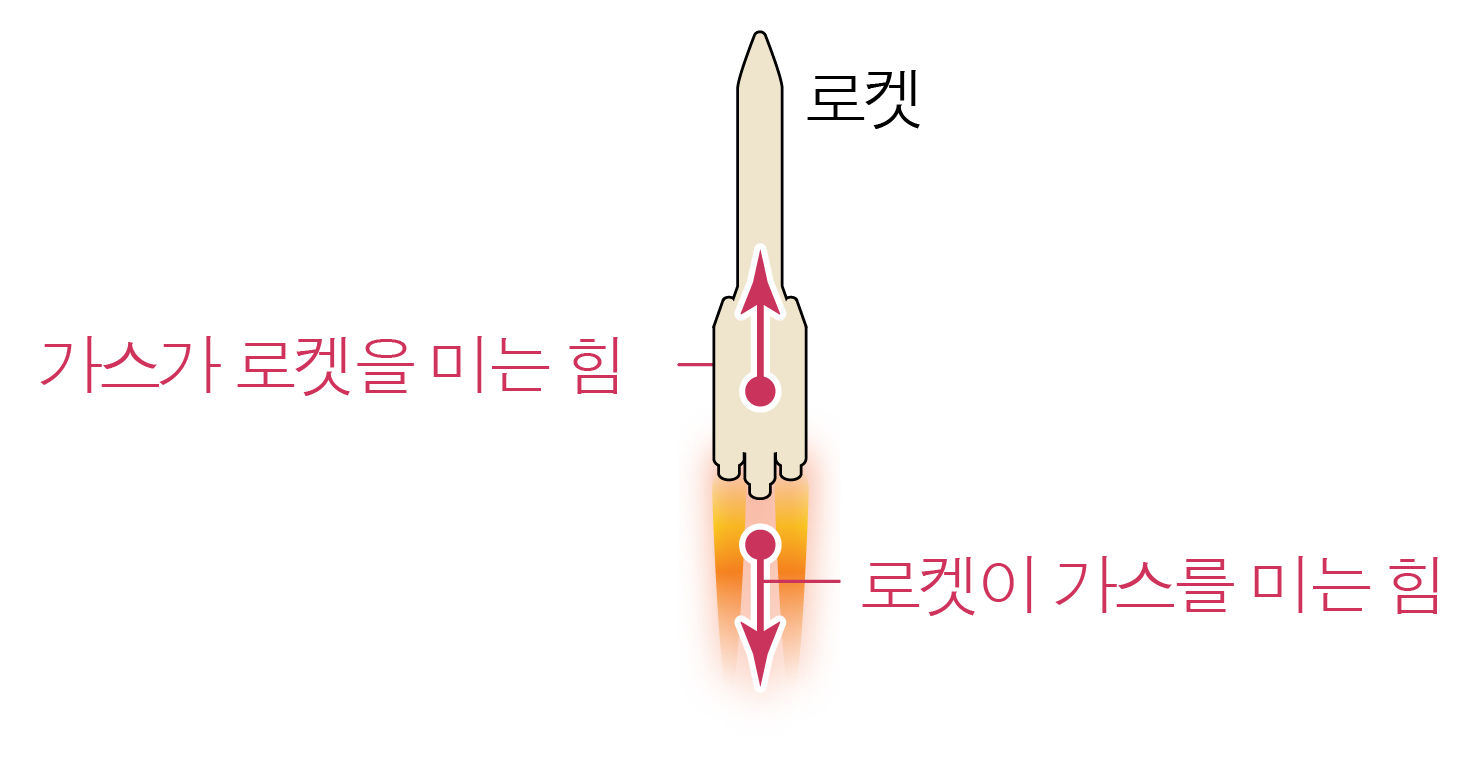
- 로켓이 가스를 분출하며 날아가는 경우:
로켓이 가스를 미는 힘만큼 그에 대한 반작용으로 가스도 로켓을 밀어 로켓이 위로 날아간다.
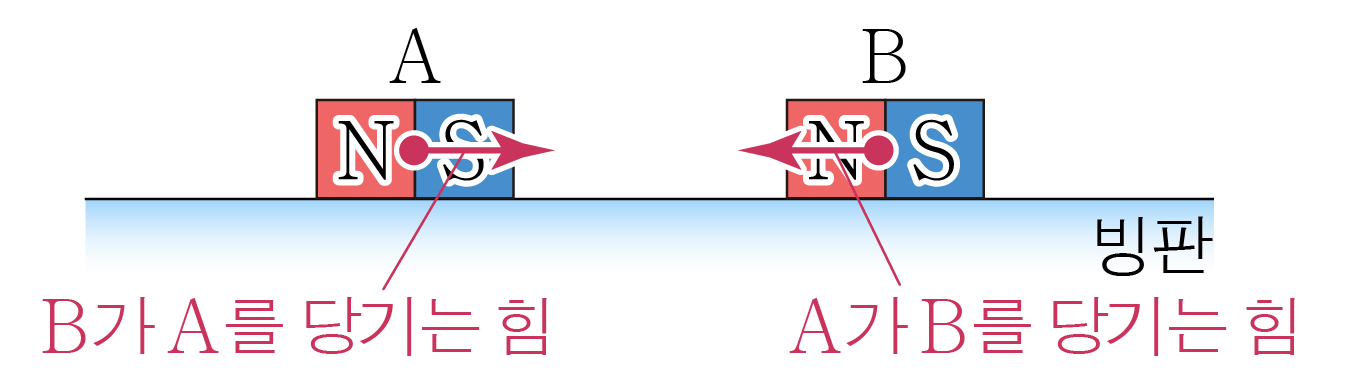
- 서로 다른 극을 마주보도록 동일한 자석 , 를 빙판 위에 놓은 경우:
자석 가 를 끌어당기는 힘만큼 도 를 끌어당기므로 와 가 서로 가까워지는 방향으로 움직인다.
¶ 작용·반작용 법칙을 통한 힘의 분석 예시
¶ 물체의 가속도가 0인 경우
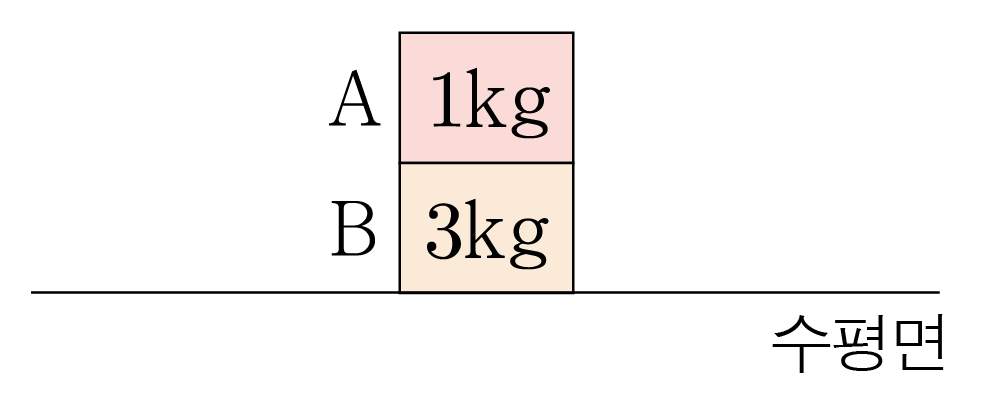
그림과 같이 수평면 위에 질량이 각각 , 인 물체 , 가 놓여 있다.
각 물체에 작용하는 힘을 분석해 보자. (단, 중력 가속도는 이다.)
각 물체에 작용하는 중력의 크기 구하기:
-
에 작용하는 중력의 크기:
$1\thinspace\mathrm{kg}\times 10\thinspace\mathrm{m/s^2}=10\thinspace\mathrm{kg· m/s^2}=10\thinspace\mathrm{N}$ -
에 작용하는 중력의 크기:
$3\thinspace\mathrm{kg}\times 10\thinspace\mathrm{m/s^2}=30\thinspace\mathrm{kg· m/s^2}=30\thinspace\mathrm{N}$
와 는 정지해 있으므로 와 에 작용하는 알짜힘은 이다.
따라서 가 를 떠받치는 힘(수직 항력)은 위 방향으로 임을 알 수 있다.
이때 작용·반작용 법칙에 의해 가 에 힘을 작용(가 를 떠받침)함과 동시에 이에 대한 반작용으로
도 에 크기가 같고 방향이 반대인 힘을 작용한다.
그러므로 에는 에 의해 아래 방향으로 크기 의 힘이 작용한다.
에 작용하는 알짜힘은 이므로 수평면이 에 작용하는 힘은 위 방향으로 이다. (마찬가지로 작용·반작용 법칙에 의해 도 수평면에 크기 의 힘을 아래 방향으로 작용한다.)
따라서 , 에 작용하는 힘을 모두 표기하면 아래 그림과 같다.
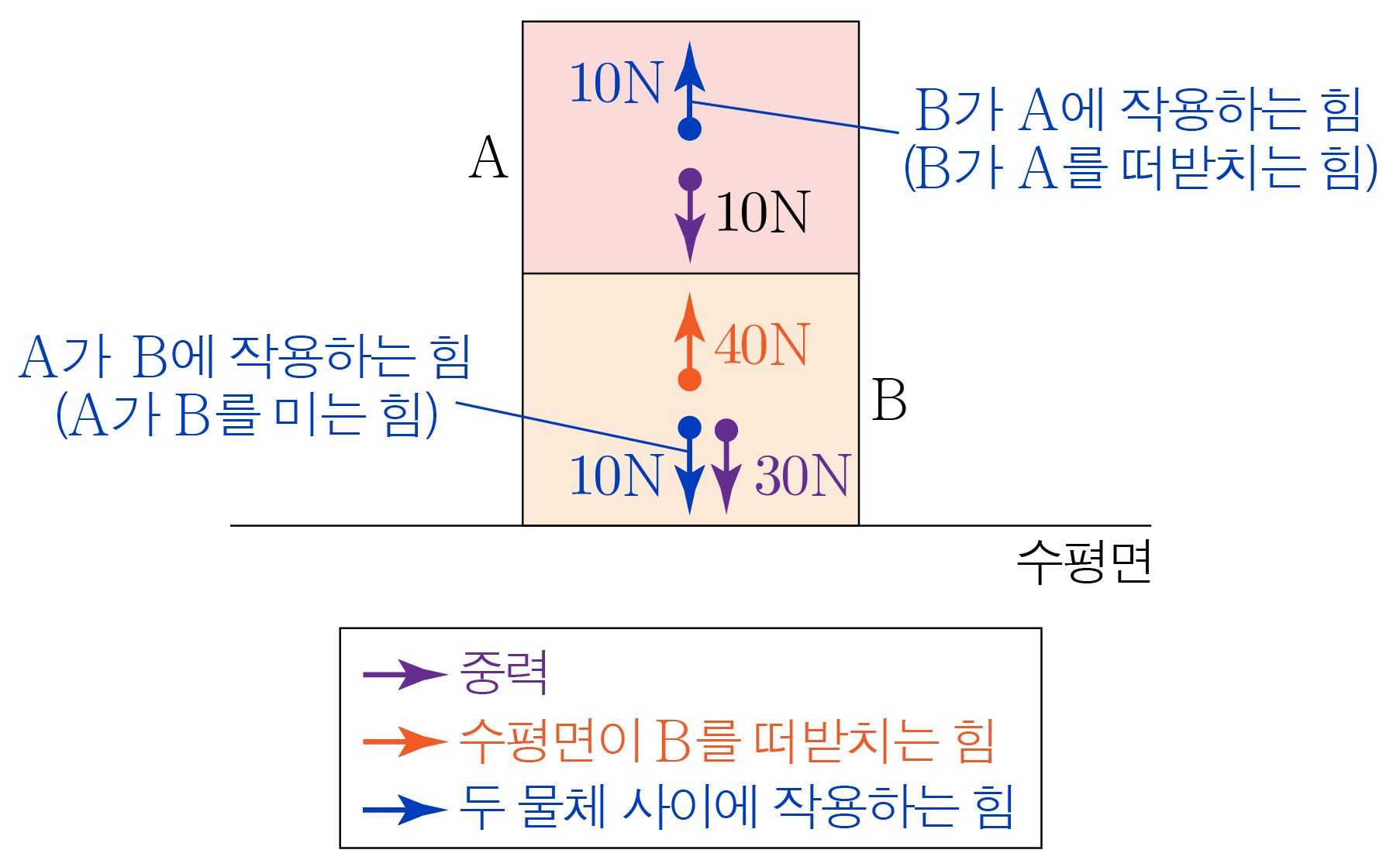
¶ 물체의 가속도가 0이 아닌 경우
그림은 질량이 각각 , 인 물체 , 가 수평 방향으로 의 힘을 받아 등가속도 직선 운동하는 모습을 나타낸 것이다.
물체의 가속도의 크기를 구해보자. (단, 중력 가속도는 이고, 모든 마찰과 공기 저항은 무시한다.)
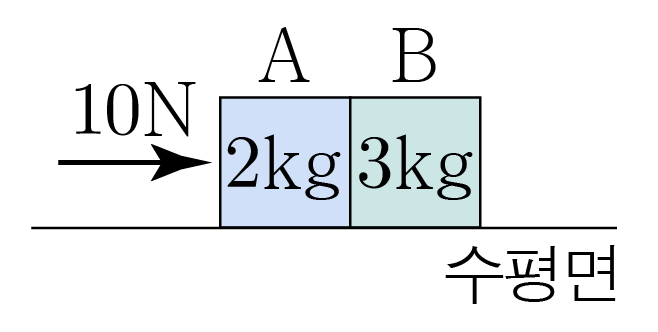
와 는 함께 움직이므로 가속도의 크기는 같다.
따라서 , 를 하나의 물체로 생각하여 가속도를 구할 수 있다.
와 를 질량이 인 한 물체로 볼 때, 물체의 가속도의 크기를 라 하면,
가속도 법칙에 의해
이다.
-
를 통해 가 에 작용하는 힘 구하기:
의 가속도는 오른쪽 방향으로 크기는 이므로
에 작용하는 알짜힘은 오른쪽 방향으로 이다.
따라서 가 에 작용하는 힘은 왼쪽 방향으로 크기가 임을 알 수 있다. -
를 통해 가 에 작용하는 힘 구하기:
의 가속도는 오른쪽 방향으로 크기는 이므로
에 작용하는 알짜힘은 오른쪽 방향으로 이고,
이는 가 에 작용하는 힘에 해당한다.
이를 통해 가 에 작용하는 힘과 가 에 작용하는 힘은 크기가 같고 방향이 서로 반대로, 작용·반작용 법칙을 따름을 알 수 있다.
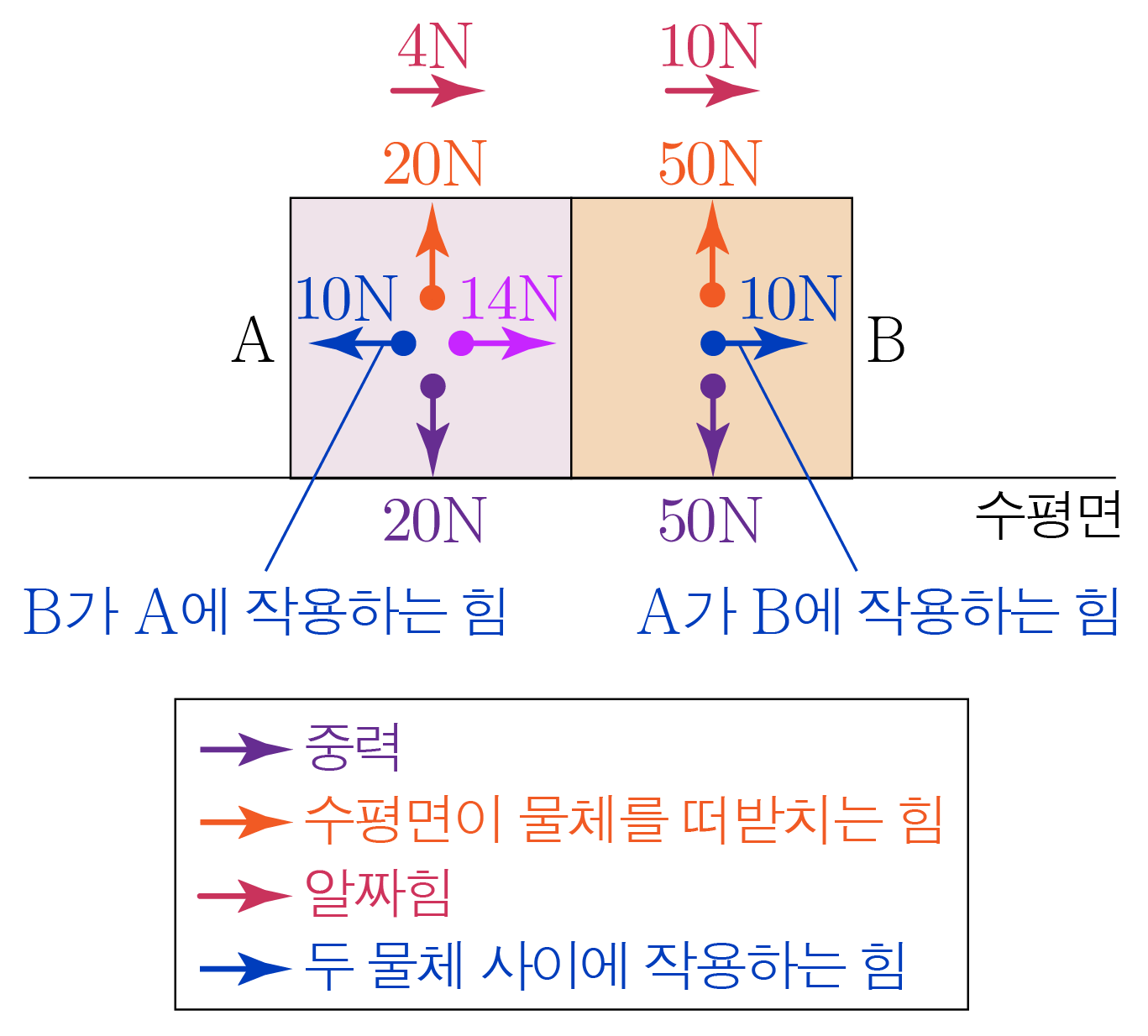
앞서 구한 내용을 바탕으로 , 에 작용하는 힘을 모두 표기하면 아래 그림과 같다.
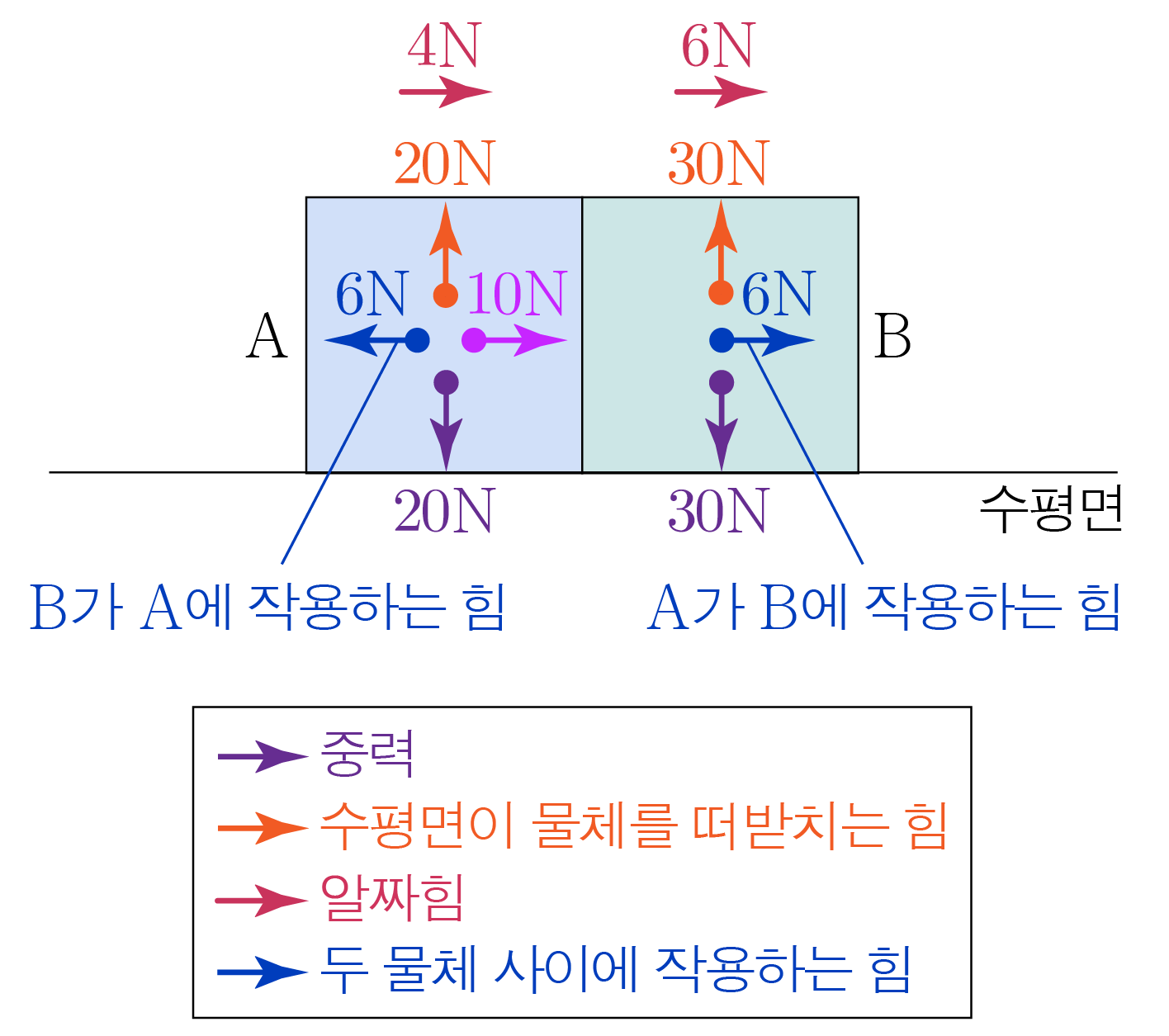
¶ 적용 문항
¶ 1번 문항

정답: $2$
ㄱ. 에 작용하는 중력은 지구가 를 당기는 힘과 같고 이와 작용·반작용 관계에 있는 힘은 가 지구를 당기는 힘이다. (X)
ㄴ. 각 물체에 작용하는 중력의 크기 구하기:
-
에 작용하는 중력의 크기:
-
에 작용하는 중력의 크기:
와 는 정지해 있으므로 와 에 작용하는 알짜힘은 이다.
따라서 가 를 떠받치는 힘(수직 항력)은 위 방향으로 크기가 임을 알 수 있다.
이때 작용·반작용 법칙에 의해 도 에 크기는 같고 방향은 반대인 힘을 작용하므로,
에는 에 의해 아래 방향으로 크기가 인 힘이 작용한다. (O)
ㄷ. 에 작용하는 알짜힘은 이므로 수평면이 에 작용하는 힘은 위 방향으로 크기는 이다. (X)
앞서 구한 내용을 바탕으로 , 에 작용하는 힘을 모두 표기하면 아래 그림과 같다.
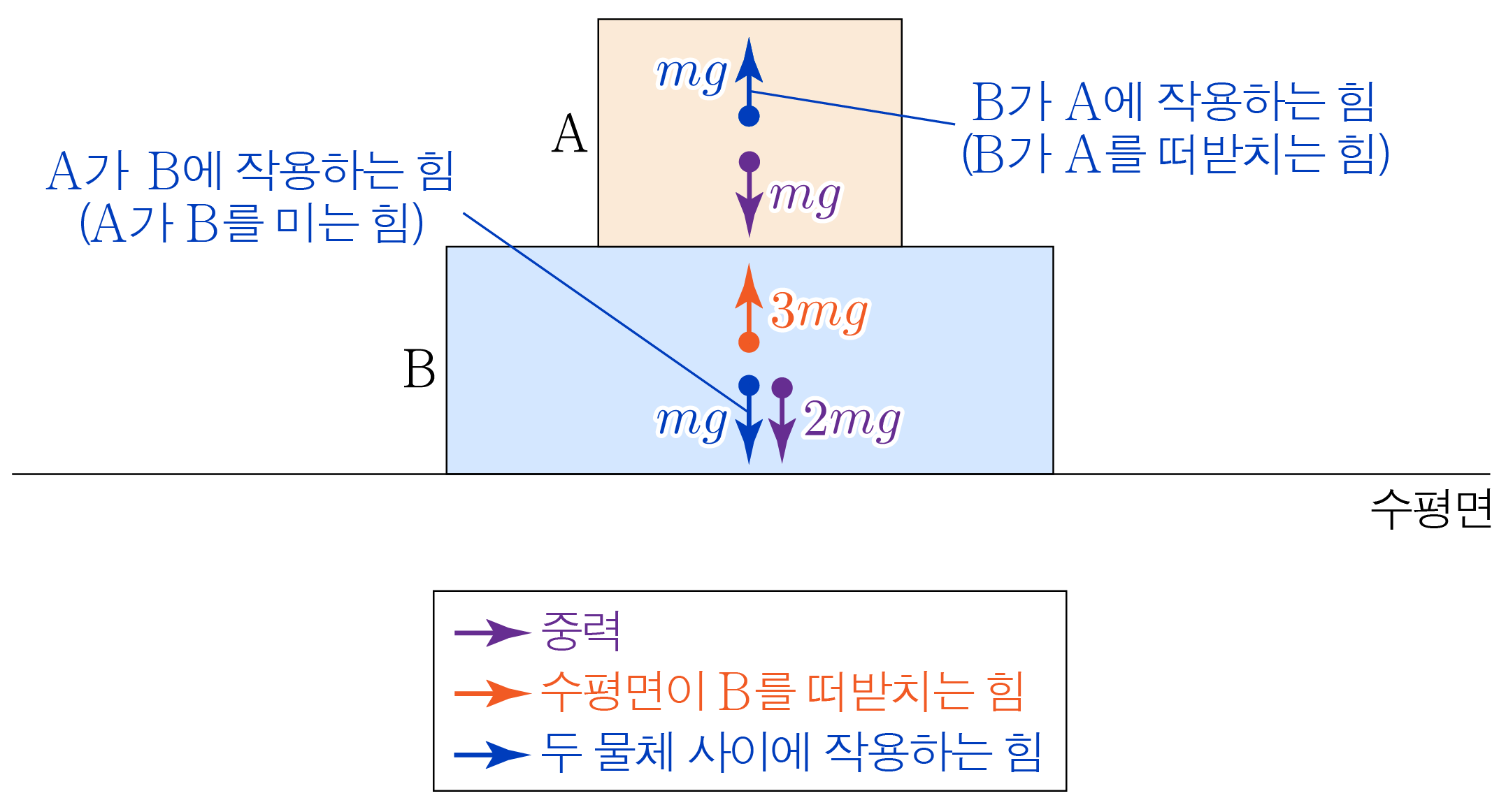
따라서 정답은 번이다.
¶ 2번 문항

정답: $2$
와 를 질량이 인 한 물체로 볼 때, 물체의 가속도의 크기를 라 하면,
가속도 법칙에 의해
이다.
-
를 통해 가 에 작용하는 힘 구하기:
의 가속도는 오른쪽 방향으로 크기는 이므로 에 작용하는 알짜힘은 오른쪽 방향으로 크기는 이다.
그러므로 가 에 작용하는 힘은 왼쪽 방향으로 크기가 임을 알 수 있다. -
를 통해 가 에 작용하는 힘 구하기:
의 가속도는 오른쪽 방향으로 크기는 이므로
에 작용하는 알짜힘은 오른쪽 방향으로 이고, 이는 가 에 작용하는 힘에 해당한다. -
를 통해 가 에 작용하는 힘 구하기:
작용·반작용 법칙에 의해 도 에 크기 의 힘을 왼쪽으로 작용하므로 가 에 작용하는 힘의 크기는 이다.
앞서 구한 내용을 바탕으로 , 에 작용하는 힘을 모두 표기하면 아래 그림과 같다.
따라서 정답은 번이다.


