해당 지식
하위 지식
상위 지식
$-$
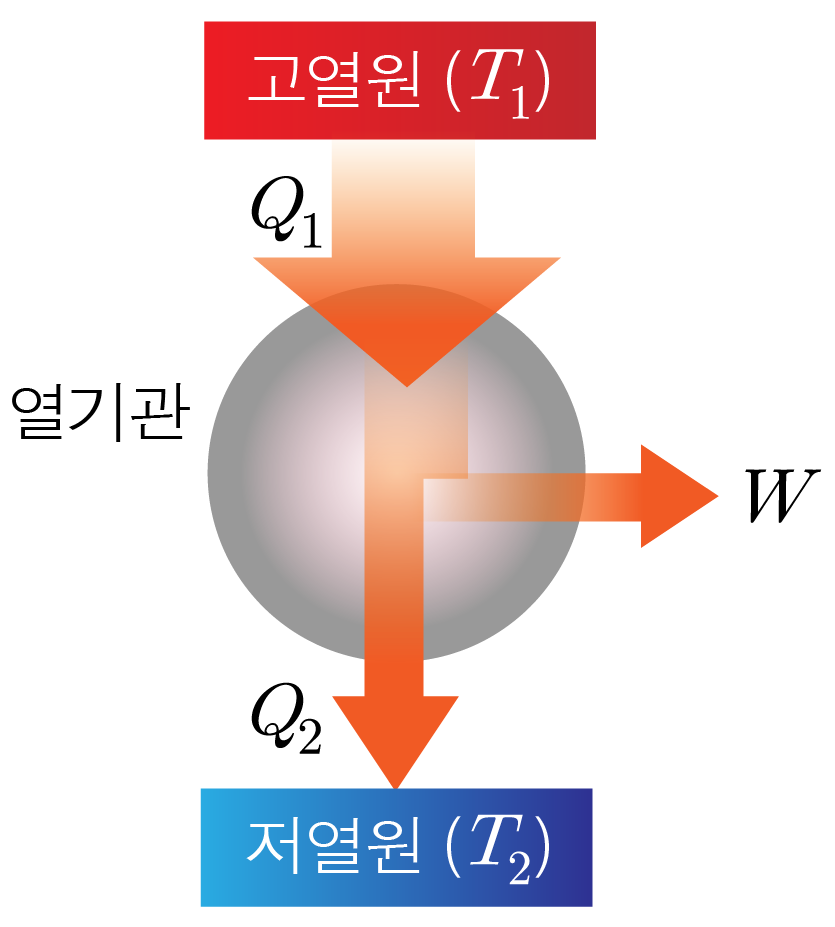
열역학 과정이 반복되는 순환 과정을 거쳐 열을 일로 바꾸는 장치이다.
기체는 1 1 Q 1 Q 1 W W Q 2 Q 2
기체는 1 1 1 1 Δ U = 0 Δ U = 0 Q 1 = W + Q 2 Q 1 = W + Q 2
열기관의 열효율을 e e 1 1 Q 1 Q 1 Q 2 Q 2 W W e = Q 1 − Q 2 Q 1 = W Q 1 e = Q 1 Q 1 − Q 2 = Q 1 W
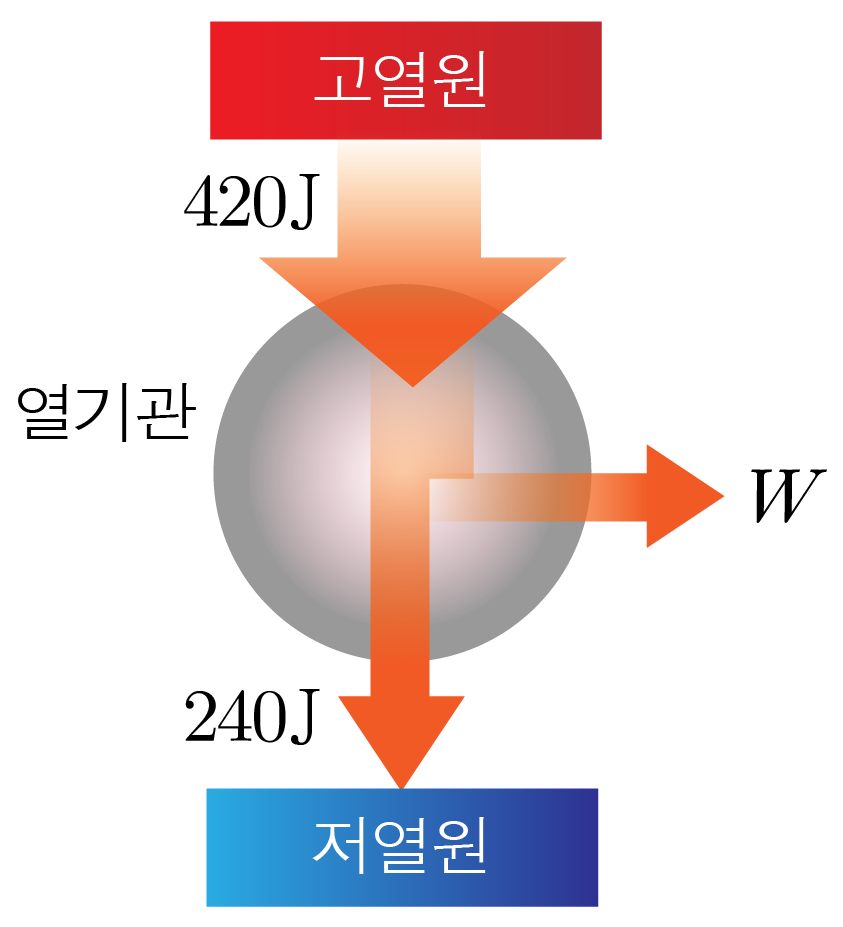
그림은 열효율이 e e 1 1 420 J 4 2 0 J W W 240 J 2 4 0 J W W e e
기체가 1 1 Q 1 Q 1 Q 2 Q 2
Q 1 = W + Q 2 Q 1 = W + Q 2 420 J = W + 240 J , 4 2 0 J = W + 2 4 0 J , 420 J − 240 J = W , 4 2 0 J − 2 4 0 J = W , W = 180 J W = 1 8 0 J
e = Q 1 − Q 2 Q 1 = W Q 1 e = Q 1 Q 1 − Q 2 = Q 1 W e = 420 J − 240 J 420 J = 180 J 420 J = 3 7 e = 4 2 0 J 4 2 0 J − 2 4 0 J = 4 2 0 J 1 8 0 J = 7 3
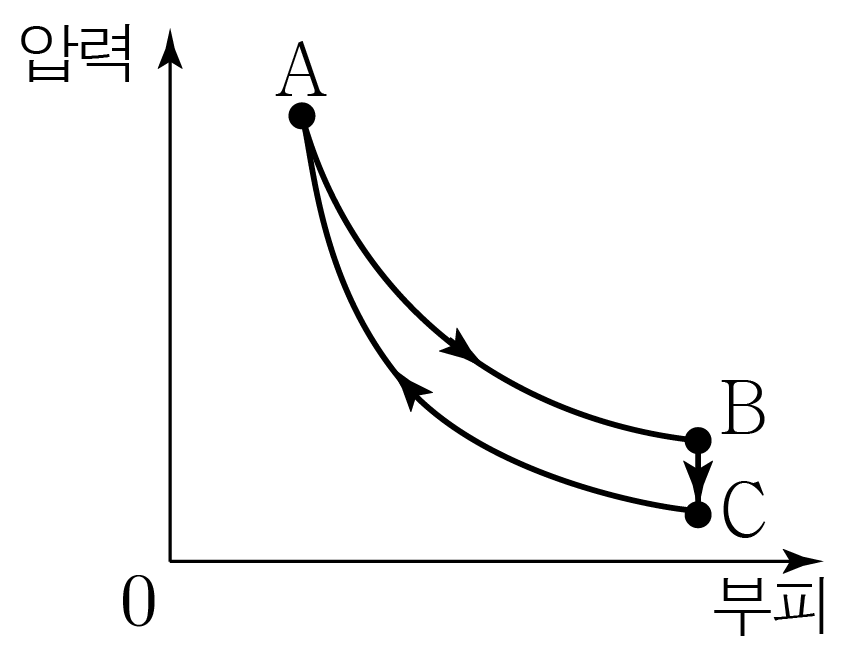
그림은 열효율이 e e A → B → C → A A → B → C → A A → B A → B B → C B → C C → A C → A A → B A → B 450 J 4 5 0 J C → A C → A 270 J 2 7 0 J 1 1 e e
A → B A → B A → B A → B Δ U = 0 Δ U = 0 Q = W Q = W W = 450 J W = 4 5 0 J Q = 450 J Q = 4 5 0 J
B → C B → C B → C B → C W = 0 W = 0 Q = Δ U Q = Δ U Δ U = x Δ U = x Q = x Q = x
C → A C → A C → A C → A Q = 0 Q = 0 Δ U + W = 0 Δ U + W = 0 Δ U = 270 J Δ U = 2 7 0 J W = − 270 J W = − 2 7 0 J
이를 표로 정리하면 아래와 같다:
과정
$Q$
$\Delta U$
$W$
$\mathrm{A} \to \mathrm{B}$
$450\,\mathrm{J}$
$0$
$450\,\mathrm{J}$
$\mathrm{B} \to \mathrm{C}$
$x$
$x$
$0$
$\mathrm{C} \to \mathrm{A}$
$0$
$270\,\mathrm{J}$
$-270\,\mathrm{J}$
1. 1 . 1 1
1 1 A → B → C → A A → B → C → A 450 J − 270 J = 180 J 4 5 0 J − 2 7 0 J = 1 8 0 J
2. 2 . 1 1
기체는 1 1 A → B → C → A A → B → C → A Δ U = 0 Δ U = 0 x + 270 J = 0 , x + 2 7 0 J = 0 , x = − 270 J x = − 2 7 0 J
이를 통해 1 1 450 J 4 5 0 J 270 J 2 7 0 J
3. 3 . e e
e = Q 1 − Q 2 Q 1 = W Q 1 e = Q 1 Q 1 − Q 2 = Q 1 W W W Q 1 Q 1 e = W Q 1 = 180 J 450 J = 2 5 e = Q 1 W = 4 5 0 J 1 8 0 J = 5 2
1번 문항 정답 및 해설 보기
정답: $5$
ㄱ. 열기관에서 기체는 고열원으로부터 열을 흡수하여 일 W W T 1 > T 2 T 1 > T 2
ㄴ. 1 1 Q 1 Q 1 Q 2 Q 2 0.3 0 . 3 e = Q 1 − Q 2 Q 1 = W Q 1 e = Q 1 Q 1 − Q 2 = Q 1 W 0.3 = Q 1 − 315 J Q 1 = W Q 1 0 . 3 = Q 1 Q 1 − 3 1 5 J = Q 1 W 0.3 = 1 − 315 J Q 1 , 0 . 3 = 1 − Q 1 3 1 5 J , 0.3 Q 1 = Q 1 − 315 J , 0 . 3 Q 1 = Q 1 − 3 1 5 J , 315 J = 0.7 Q 1 , 3 1 5 J = 0 . 7 Q 1 , Q 1 = 450 J Q 1 = 4 5 0 J
ㄷ. 1 1 Q 1 = W + Q 2 Q 1 = W + Q 2 450 J = W + 315 J , 4 5 0 J = W + 3 1 5 J , 450 J − 315 J = W , 4 5 0 J − 3 1 5 J = W , W = 135 J W = 1 3 5 J
따라서 정답은 5 5
2번 문항 정답 및 해설 보기
정답: $2$
A → B A → B A → B A → B W = 0 W = 0 Q = Δ U Q = Δ U P P V V 3 2 P V 2 3 P V A A 3 2 P 0 V 0 2 3 P 0 V 0 B B 3 2 × ( 2 P 0 ) × V 0 = 3 P 0 V 0 2 3 × ( 2 P 0 ) × V 0 = 3 P 0 V 0 Δ U = Q = 3 P 0 V 0 − 3 2 P 0 V 0 = 3 2 P 0 V 0 Δ U = Q = 3 P 0 V 0 − 2 3 P 0 V 0 = 2 3 P 0 V 0
B → C B → C B → C B → C Δ V Δ V Δ U = 3 2 P Δ V Δ U = 2 3 P Δ V W = P Δ V W = P Δ V B → C B → C Δ V = V 0 Δ V = V 0 Δ U = 3 2 × 2 P 0 × V 0 = 3 P 0 V 0 Δ U = 2 3 × 2 P 0 × V 0 = 3 P 0 V 0 W = 2 P 0 V 0 W = 2 P 0 V 0 Q = 3 P 0 V 0 + 2 P 0 V 0 = 5 P 0 V 0 Q = 3 P 0 V 0 + 2 P 0 V 0 = 5 P 0 V 0
C → D C → D C → D C → D W = 0 W = 0 Q = Δ U Q = Δ U C C 3 2 × ( 2 P 0 ) × ( 2 V 0 ) = 6 P 0 V 0 2 3 × ( 2 P 0 ) × ( 2 V 0 ) = 6 P 0 V 0 D D 3 2 × P 0 × ( 2 V 0 ) = 3 P 0 V 0 2 3 × P 0 × ( 2 V 0 ) = 3 P 0 V 0 Δ U = Q = 3 P 0 V 0 − 6 P 0 V 0 = − 3 P 0 V 0 Δ U = Q = 3 P 0 V 0 − 6 P 0 V 0 = − 3 P 0 V 0
D → A D → A D → A D → A Δ V Δ V Δ U = 3 2 P Δ V Δ U = 2 3 P Δ V W = P Δ V W = P Δ V D → A D → A Δ V = − V 0 Δ V = − V 0 Δ U = 3 2 × P 0 × ( − V 0 ) = − 3 2 P 0 V 0 Δ U = 2 3 × P 0 × ( − V 0 ) = − 2 3 P 0 V 0 W = P 0 × ( − V 0 ) = − P 0 V 0 W = P 0 × ( − V 0 ) = − P 0 V 0 Q = − 3 2 P 0 V 0 − P 0 V 0 = − 5 2 P 0 V 0 Q = − 2 3 P 0 V 0 − P 0 V 0 = − 2 5 P 0 V 0
이를 표로 정리하면 아래와 같다:
과정
$Q$
$\Delta U$
$W$
$\mathrm{A} \to \mathrm{B}$
$\frac{3}{2}P_0V_0$
$\frac{3}{2}P_0V_0$
$0$
$\mathrm{B} \to \mathrm{C}$
$5P_0V_0$
$3P_0V_0$
$2P_0V_0$
$\mathrm{C} \to \mathrm{D}$
$-3P_0V_0$
$-3P_0V_0$
$0$
$\mathrm{D} \to \mathrm{A}$
$-\frac{5}{2}P_0V_0$
$-\frac{3}{2}P_0V_0$
$-P_0V_0$
1. 1 . 1 1
1 1 A → B → C → D → A A → B → C → D → A W = 2 P 0 V 0 − P 0 V 0 = P 0 V 0 W = 2 P 0 V 0 − P 0 V 0 = P 0 V 0
2. 2 . 1 1 Q 1 Q 1
Q 1 = 3 2 P 0 V 0 + 5 P 0 V 0 , Q 1 = 2 3 P 0 V 0 + 5 P 0 V 0 , Q 1 = 13 2 P 0 V 0 Q 1 = 2 1 3 P 0 V 0
3. 3 . e e
e = Q 1 − Q 2 Q 1 = W Q 1 e = Q 1 Q 1 − Q 2 = Q 1 W W W Q 1 Q 1 e = W Q 1 = P 0 V 0 13 2 P 0 V 0 = 2 13 e = Q 1 W = 2 1 3 P 0 V 0 P 0 V 0 = 1 3 2
따라서 정답은 2 2
