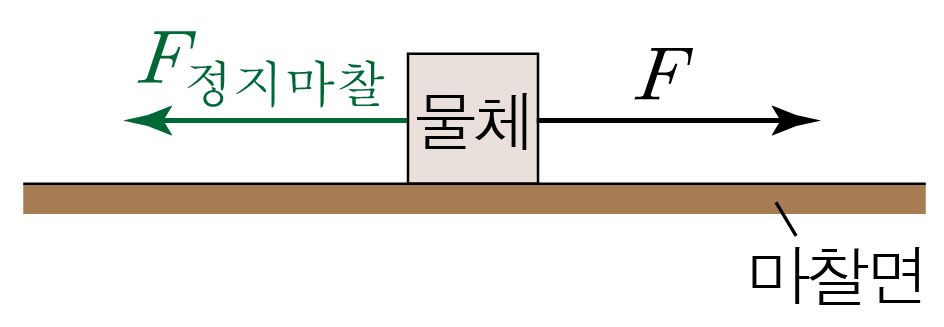
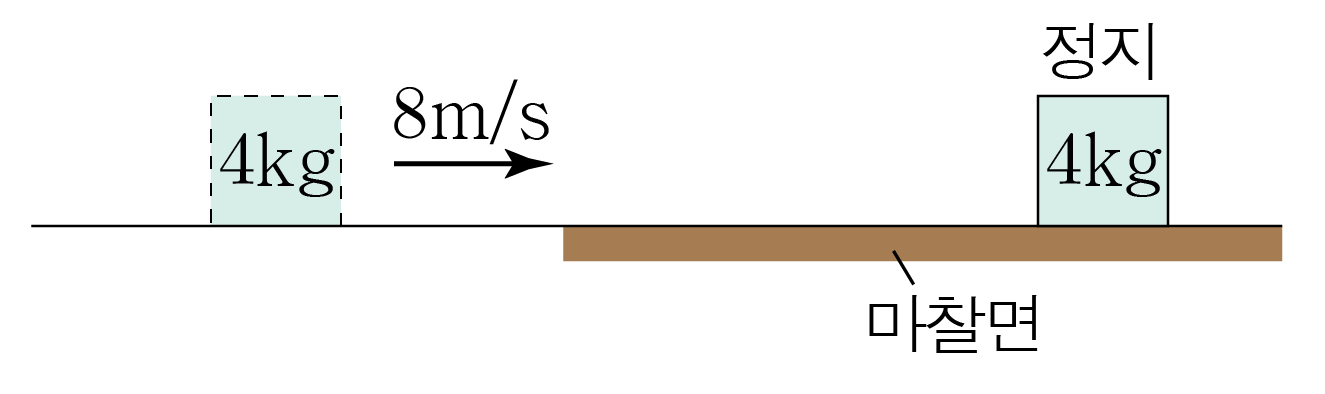두 물체가 서로 접촉하여 누르고 있고 물체가 운동하거나 운동하려고 할 때 물체의 운동을 방해하는 방향으로 작용하는 힘이다.
마찰력의 크기를 F 마찰 F 마 찰 μ μ N N F 마찰 = μ N F 마 찰 = μ N μ μ
물체가 정지해 있을 때 작용하는 마찰력으로, 물체에 작용하는 외부 힘 F → F
정지 마찰력은 물체에 작용하는 접촉면 방향의 알짜힘이 0 0 F → F F → 정지마찰 F 정 지 마 찰
최대 정지 마찰력의 크기를 F 최대정지마찰 F 최 대 정 지 마 찰 μ 정지 μ 정 지 N N F 최대정지마찰 = μ 정지 N F 최 대 정 지 마 찰 = μ 정 지 N
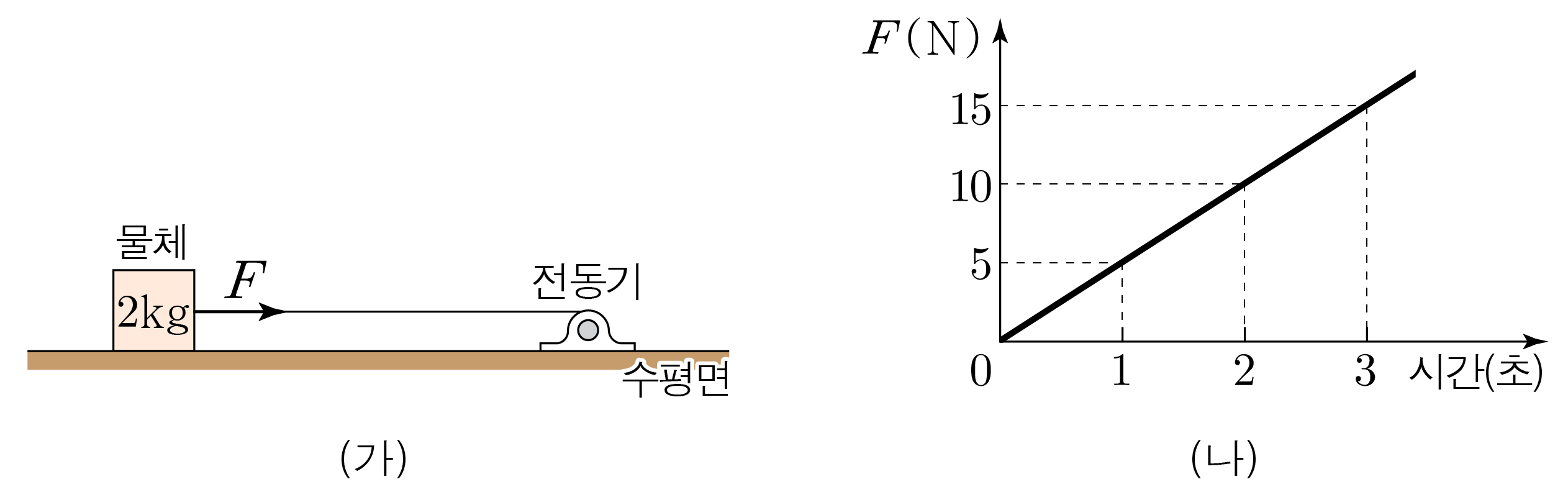
그림 (가)는 0 s 0 s 2 k g 2 k g F → F 2 s 2 s 10 m / s 2 1 0 m / s 2
물체는 0 s 0 s 2 s 2 s F → F F → F 2 s 2 s 10 N 1 0 N
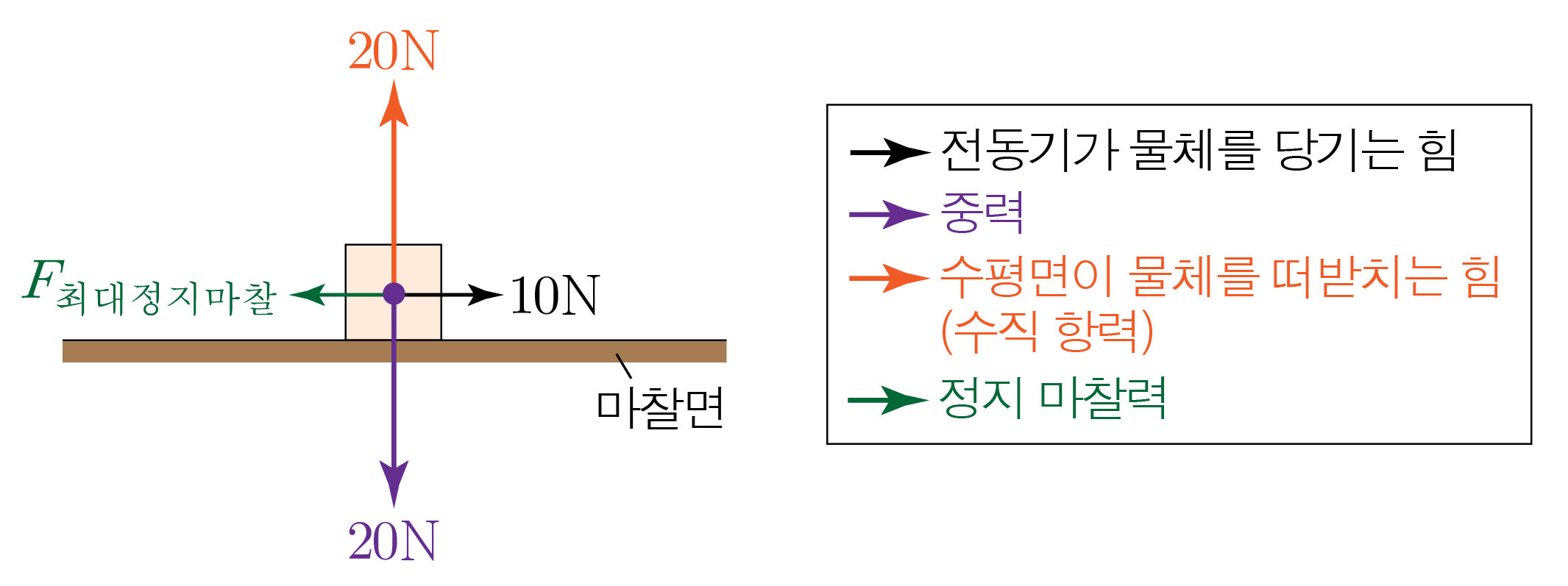
이때 물체의 질량은 2 k g 2 k g 2 k g × 10 m / s 2 = 20 k g ⋅ m / s 2 = 20 N 2 k g × 1 0 m / s 2 = 2 0 k g ⋅ m / s 2 = 2 0 N 20 N 2 0 N
앞서 구한 내용을 바탕으로 2 2
따라서 F 최대정지마찰 = μ 정지 N F 최 대 정 지 마 찰 = μ 정 지 N 10 N = μ 정지 × 20 N , 1 0 N = μ 정 지 × 2 0 N , μ 정지 = 0.5 μ 정 지 = 0 . 5
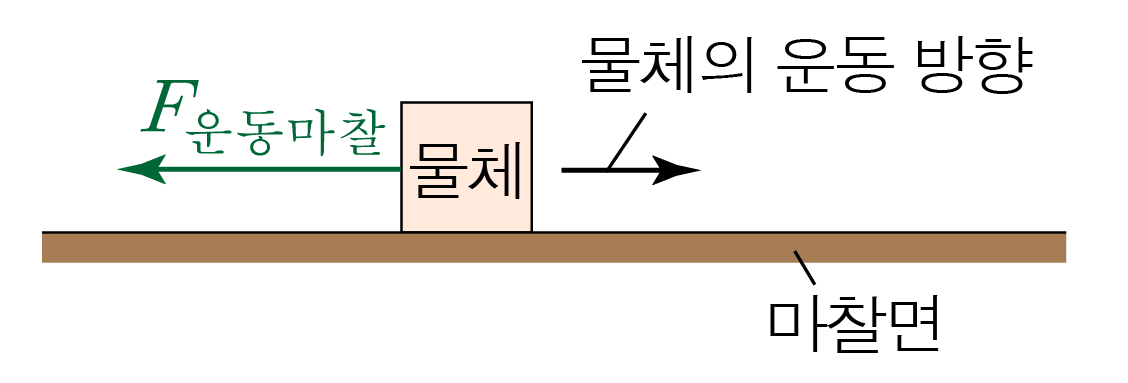
물체가 운동할 때 작용하는 마찰력으로, 방향은 물체의 운동 방향의 반대이다.
운동 마찰력의 크기를 F 운동마찰 F 운 동 마 찰 μ 운동 μ 운 동 N N F 운동마찰 = μ 운동 N F 운 동 마 찰 = μ 운 동 N
운동 마찰 계수는 정지 마찰 계수보다 작거나 같다.
따라서 정지 상태의 물체를 가속시키는 것보다 이미 움직이고 있는 물체를 가속시키는 것이 더 쉽다.
그림과 같이 질량이 4 k g 4 k g 8 m / s 8 m / s 2 s 2 s μ μ μ μ 10 m / s 2 1 0 m / s 2
물체는 마찰 구간에 8 m / s 8 m / s 2 s 2 s 8 m / s 2 s = 4 m / s 2 2 s 8 m / s = 4 m / s 2
물체에 작용하는 알짜힘은 운동 마찰력과 같으므로 가속도 법칙을 통해 물체에 작용하는 운동 마찰력의 크기는 4 k g × 4 m / s 2 = 16 k g ⋅ m / s 2 = 16 N 4 k g × 4 m / s 2 = 1 6 k g ⋅ m / s 2 = 1 6 N
이때 물체의 질량은 4 k g 4 k g 4 k g × 10 m / s 2 = 40 k g ⋅ m / s 2 = 40 N 4 k g × 1 0 m / s 2 = 4 0 k g ⋅ m / s 2 = 4 0 N 40 N 4 0 N
따라서 F 운동마찰 = μ 운동 N F 운 동 마 찰 = μ 운 동 N 16 N = μ × 40 N , 1 6 N = μ × 4 0 N , μ = 0.4 μ = 0 . 4
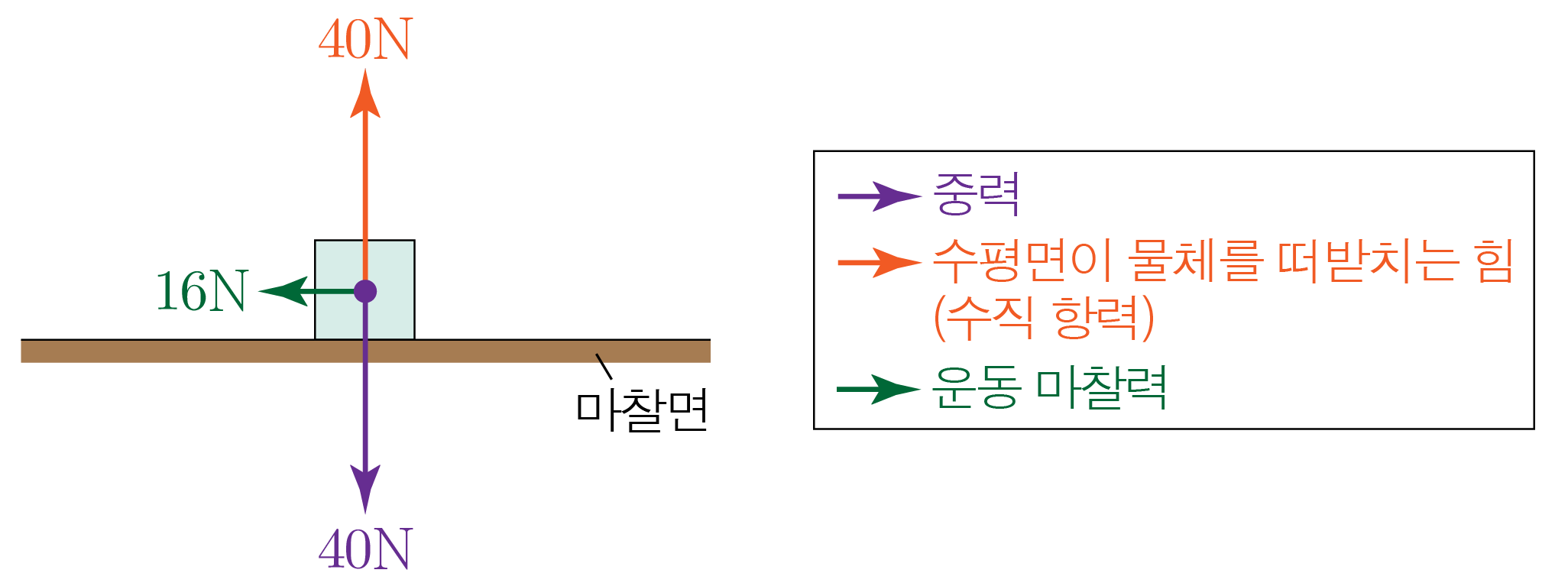
앞서 구한 내용을 바탕으로 마찰면에서 물체가 등가속도 운동을 하는 동안 물체에 작용하는 모든 힘을 표기하면 아래 그림과 같다.
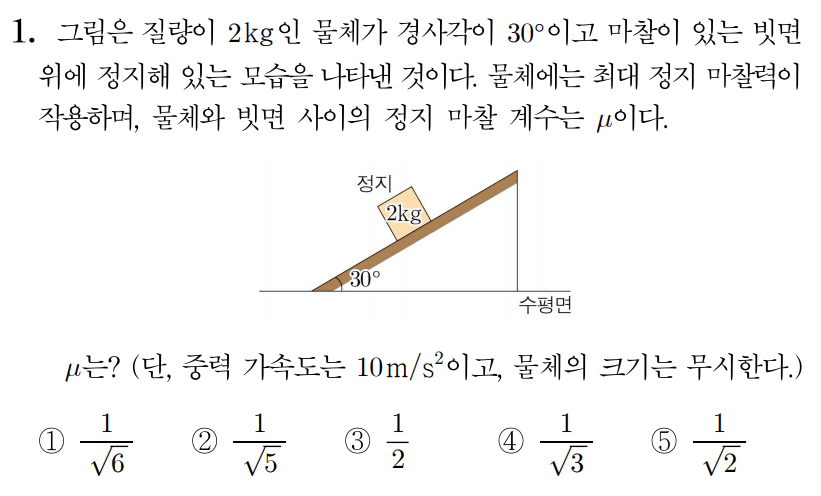
1번 문항 정답 및 해설 보기
정답: $4$
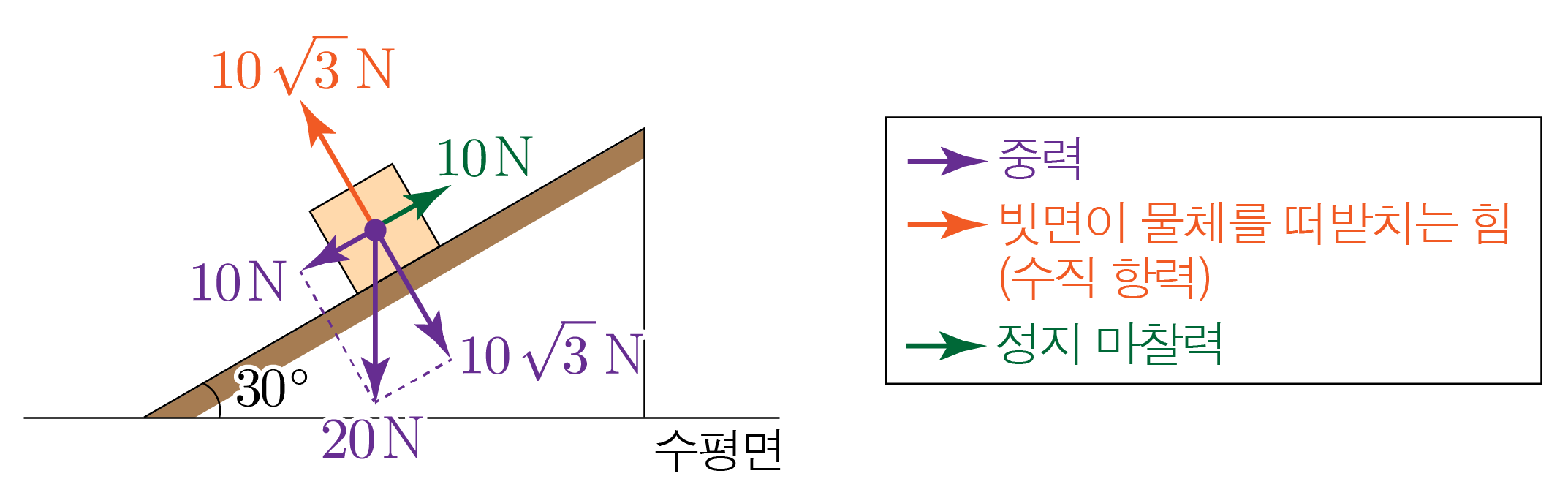
중력을 빗면에 나란한 방향과 수직인 방향으로 분해하기:
빗면에 나란한 방향으로 분해한 힘의 크기:2 k g × 10 m / s 2 × sin 3 0 ∘ = 20 k g ⋅ m / s 2 × sin 3 0 ∘ = 20 N × 1 2 = 10 2 k g × 1 0 m / s 2 × sin 3 0 ∘ = 2 0 k g ⋅ m / s 2 × sin 3 0 ∘ = 2 0 N × 2 1 = 1 0
빗면에 수직인 방향으로 분해한 힘의 크기:2 k g × 10 m / s 2 × cos 3 0 ∘ = 20 k g ⋅ m / s 2 × cos 3 0 ∘ = 20 N × 3 2 = 10 3 2 k g × 1 0 m / s 2 × cos 3 0 ∘ = 2 0 k g ⋅ m / s 2 × cos 3 0 ∘ = 2 0 N × 2 3 = 1 0 3
물체는 정지해 있으므로 빗면에 나란한 방향으로 분해한 힘의 크기는 정지 마찰력의 크기와 같다.10 N 1 0 N
또한 빗면에 수직인 방향으로 분해한 힘의 크기는 수직 항력의 크기와 같다.
그러므로 F 최대정지마찰 = μ 정지 N F 최 대 정 지 마 찰 = μ 정 지 N 10 N = μ 정지 × 10 3 N , 1 0 N = μ 정 지 × 1 0 3 N , μ 정지 = 1 3 μ 정 지 = 3 1
앞서 구한 내용을 바탕으로 물체에 작용하는 모든 힘을 표기하면 아래 그림과 같다.
따라서 정답은 4 4
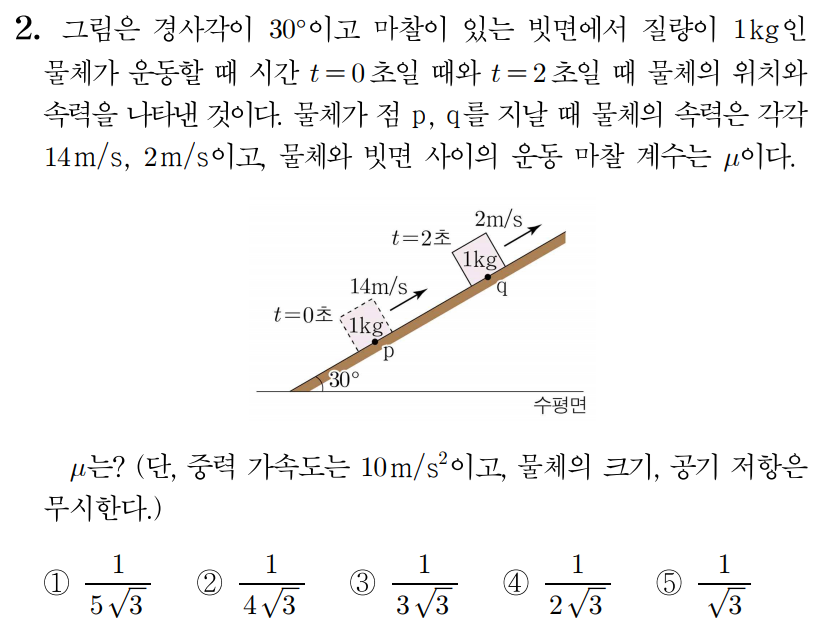
2번 문항 정답 및 해설 보기
정답: $1$
물체는 2 s 2 s 14 m / s − 2 m / s = 12 m / s 1 4 m / s − 2 m / s = 1 2 m / s 12 m / s 2 s = 6 m / s 2 2 s 1 2 m / s = 6 m / s 2
가속도 법칙을 통해 물체에 작용하는 알짜힘의 크기는 1 k g × 6 m / s 2 = 6 k g ⋅ m / s 2 = 6 N 1 k g × 6 m / s 2 = 6 k g ⋅ m / s 2 = 6 N
마찰력은 물체의 운동 방향과 반대로 작용하므로 빗면과 나란한 아래쪽 방향으로 작용한다.
중력을 빗면에 나란한 방향과 수직인 방향으로 분해하기:
빗면에 나란한 방향으로 분해한 힘의 크기:1 k g × 10 m / s 2 × sin 3 0 ∘ = 10 k g ⋅ m / s 2 × sin 3 0 ∘ = 10 N × 1 2 = 5 1 k g × 1 0 m / s 2 × sin 3 0 ∘ = 1 0 k g ⋅ m / s 2 × sin 3 0 ∘ = 1 0 N × 2 1 = 5
빗면에 수직인 방향으로 분해한 힘의 크기:1 k g × 10 m / s 2 × cos 3 0 ∘ = 10 k g ⋅ m / s 2 × cos 3 0 ∘ = 10 N × 3 2 = 5 3 1 k g × 1 0 m / s 2 × cos 3 0 ∘ = 1 0 k g ⋅ m / s 2 × cos 3 0 ∘ = 1 0 N × 2 3 = 5 3
빗면에 수직인 방향으로 분해한 힘의 크기는 수직 항력의 크기와 같으므로F 운동마찰 = μ 운동 N F 운 동 마 찰 = μ 운 동 N F 운동마찰 = μ × 5 3 N = 5 3 μ N F 운 동 마 찰 = μ × 5 3 N = 5 3 μ N
①에 의해 물체에 작용하는 알짜힘은 빗면에 나란한 방향으로 분해한 중력과 마찰력의 합과 같으므로6 N = 5 N + 5 3 μ N , 6 N = 5 N + 5 3 μ N , 1 N = 5 3 μ N , 1 N = 5 3 μ N , 1 = 5 3 μ , 1 = 5 3 μ , μ = 1 5 3 μ = 5 3 1
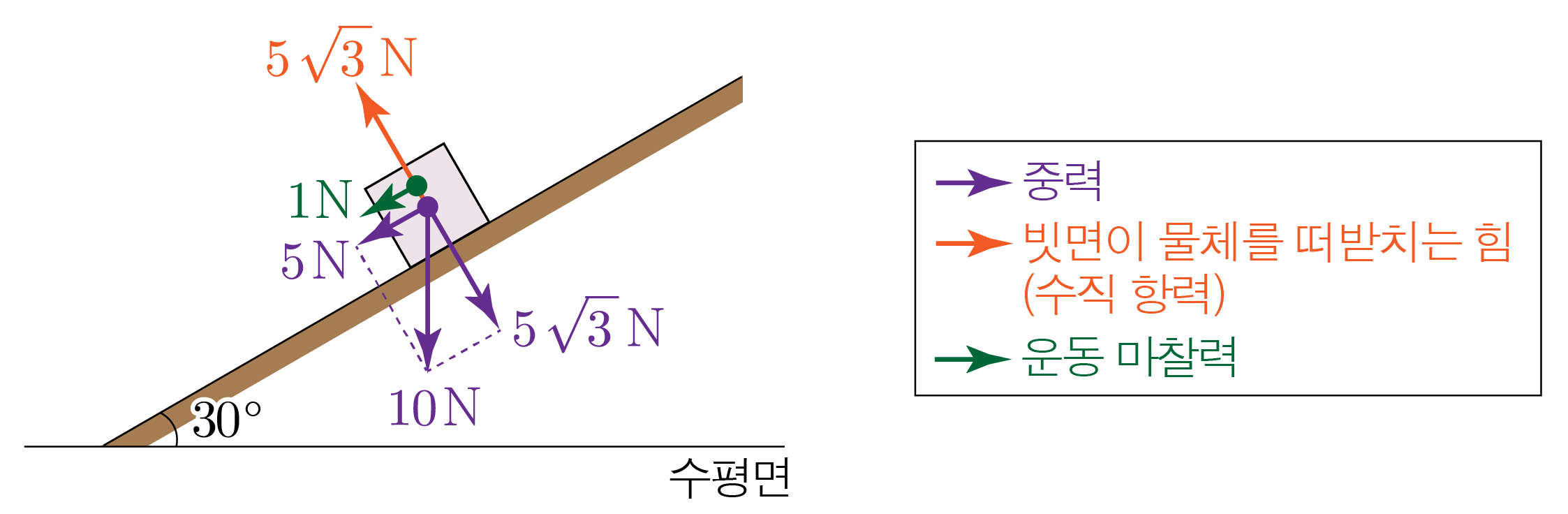
앞서 구한 내용을 바탕으로 물체에 작용하는 모든 힘을 표기하면 아래 그림과 같다.
따라서 정답은 1 1