¶ 지식 정보
¶ 등가속도 운동
가속도가 이 아닌 일정한 값을 갖는 운동이다.
¶ 등가속도 운동하는 물체의 평균 속도
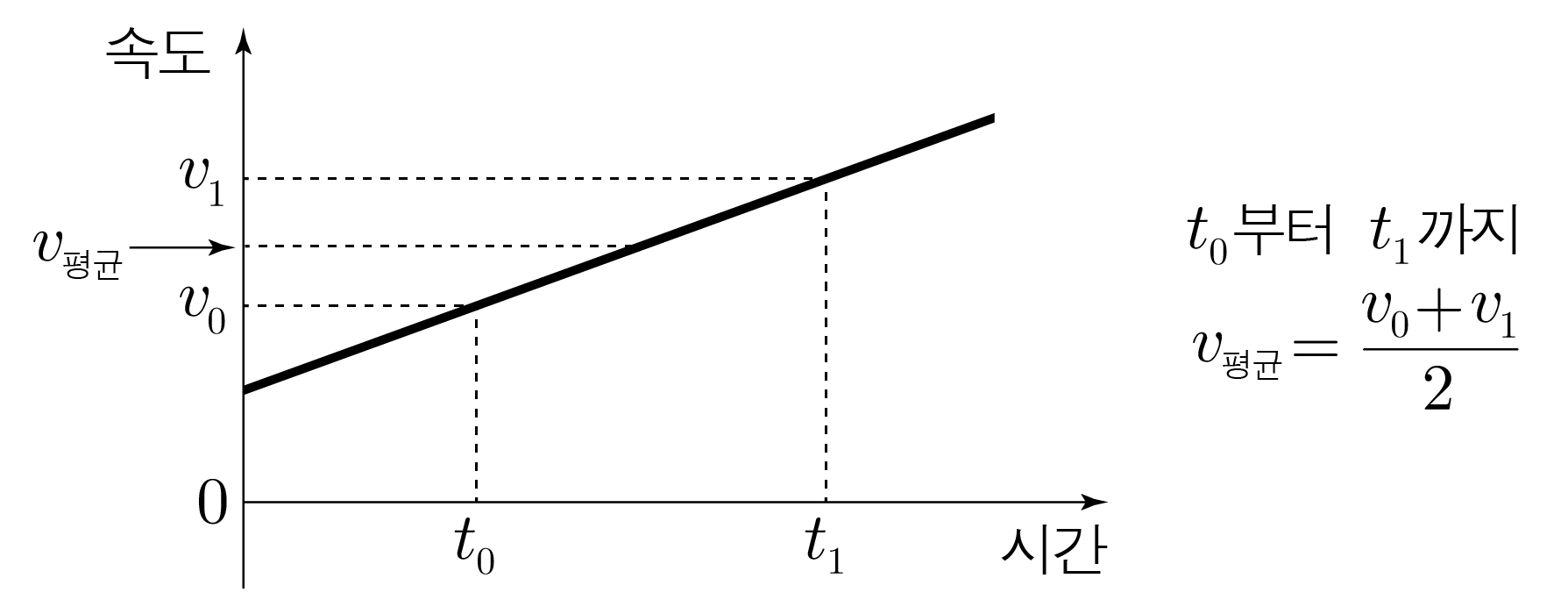
처음 속도와 나중 속도의 중간 값이다.
처음 속도와 나중 속도를 각각 이라 하면, 평균 속도는 이다.
등가속도 운동하는 물체의 속도시간 그래프를 그리면 가속도(그래프의 기울기)가 일정하기 때문에 아래 그림과 같이 직선 형태의 그래프가 나타난다.
¶ 등가속도 운동하는 물체의 속도-시간 그래프 분석 예시
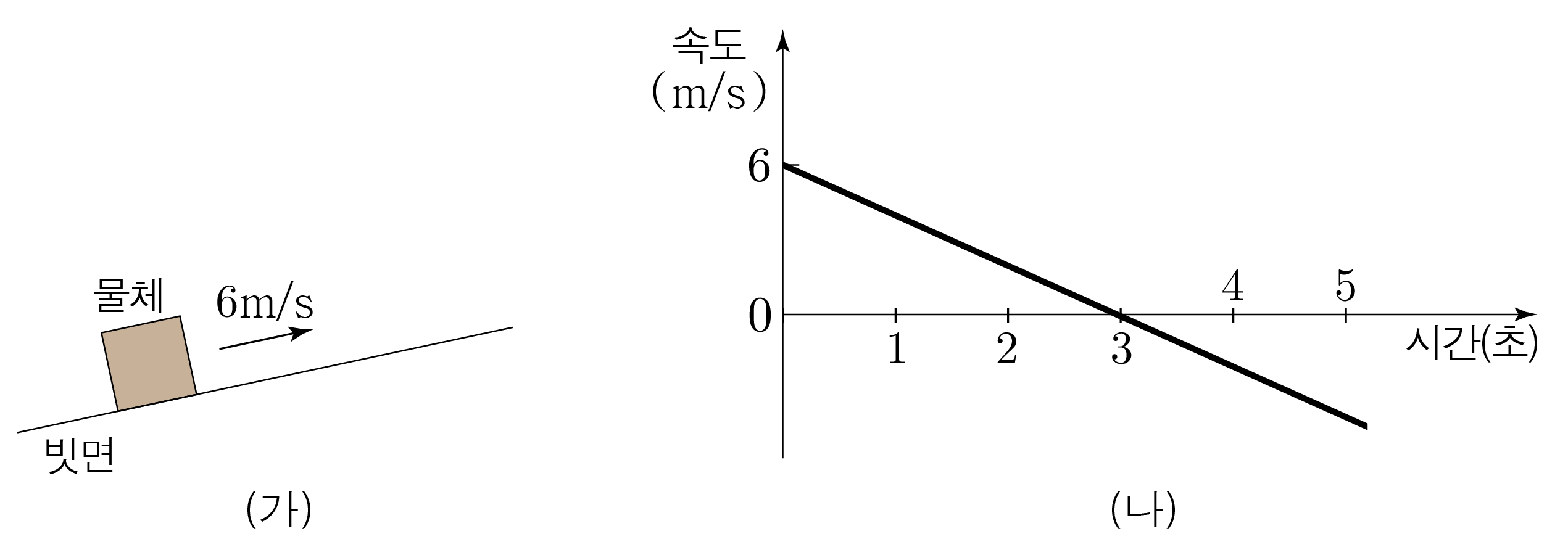
그림 (가)는 빗면에서 등가속도 운동하는 물체를, (나)는 물체의 속도시간 그래프를 나타낸 것이다.
물체의 속도시간 그래프를 분석해보자. (단, 속도의 방향은 빗면을 올라가는 방향이 양이다.)
-
방향 정보:
부터 까지 물체의 속도는 양의 부호를 가지므로 빗면을 올라감을 알 수 있고,
이후부터 물체의 속도는 음의 부호를 가지므로 물체는 빗면을 내려간다.
-
가속도 정보:
동안 물체의 속도는 만큼 변했으므로
가속도(단위 시간 동안 속도 변화)는 이다.
-
속도 정보:
물체의 가속도는 이므로
일 때 물체의 속도는 이다.
-
평균 속도 정보:
부터 까지 물체의 평균 속도는 이고,
부터 까지 물체의 평균 속도는 이다.
-
이동 거리 정보:
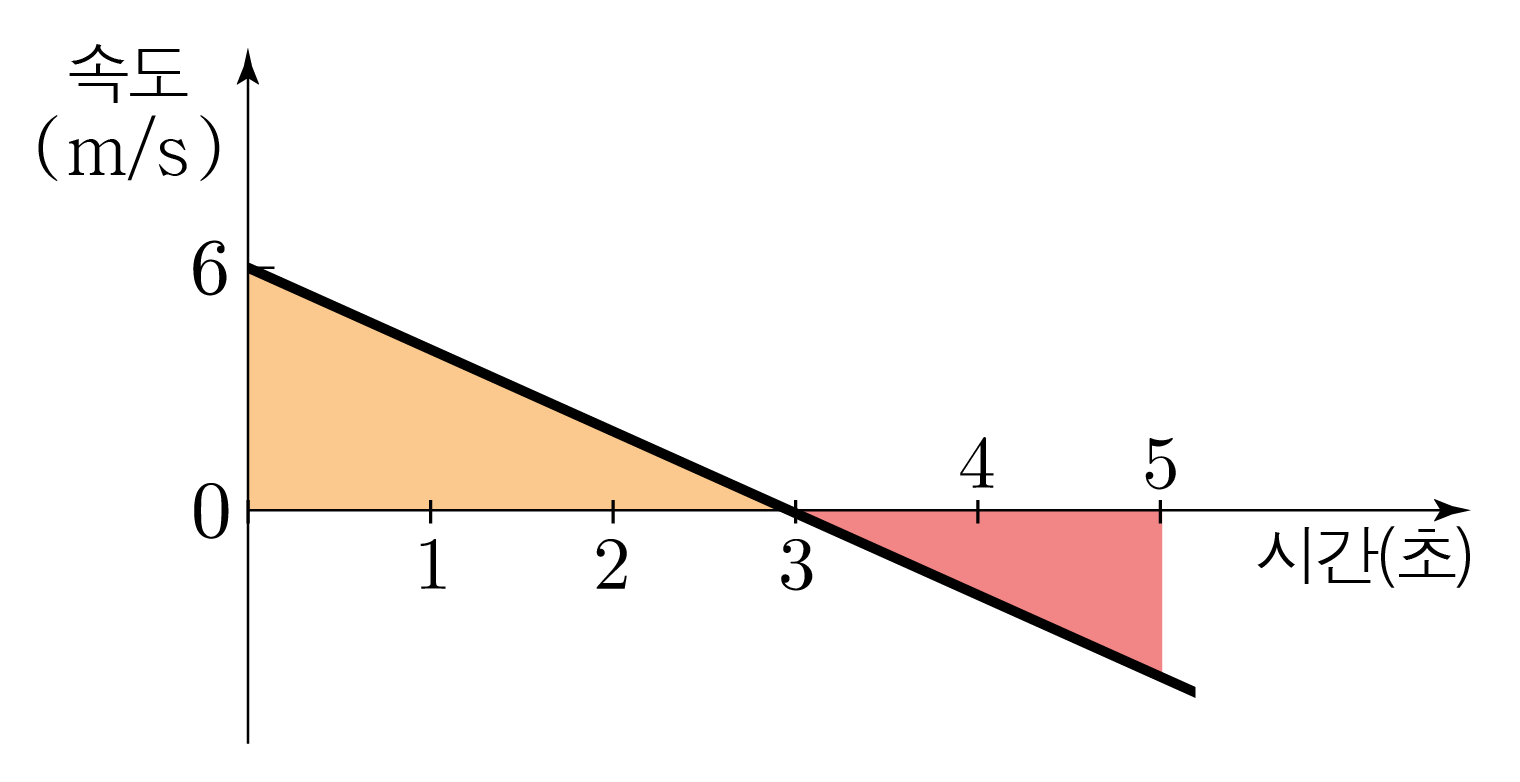
부터 까지 물체의 이동 거리는 아래 그림의 주황색 부분의 면적에 해당하므로
이다.
부터 까지 물체의 이동 거리는 아래 그림의 분홍색 부분의 면적에 해당하므로
이다.
평균 속력을 이용하면 부터 까지 물체의 이동 거리는
부터 까지 물체의 이동 거리는 로 구할 수 있다.
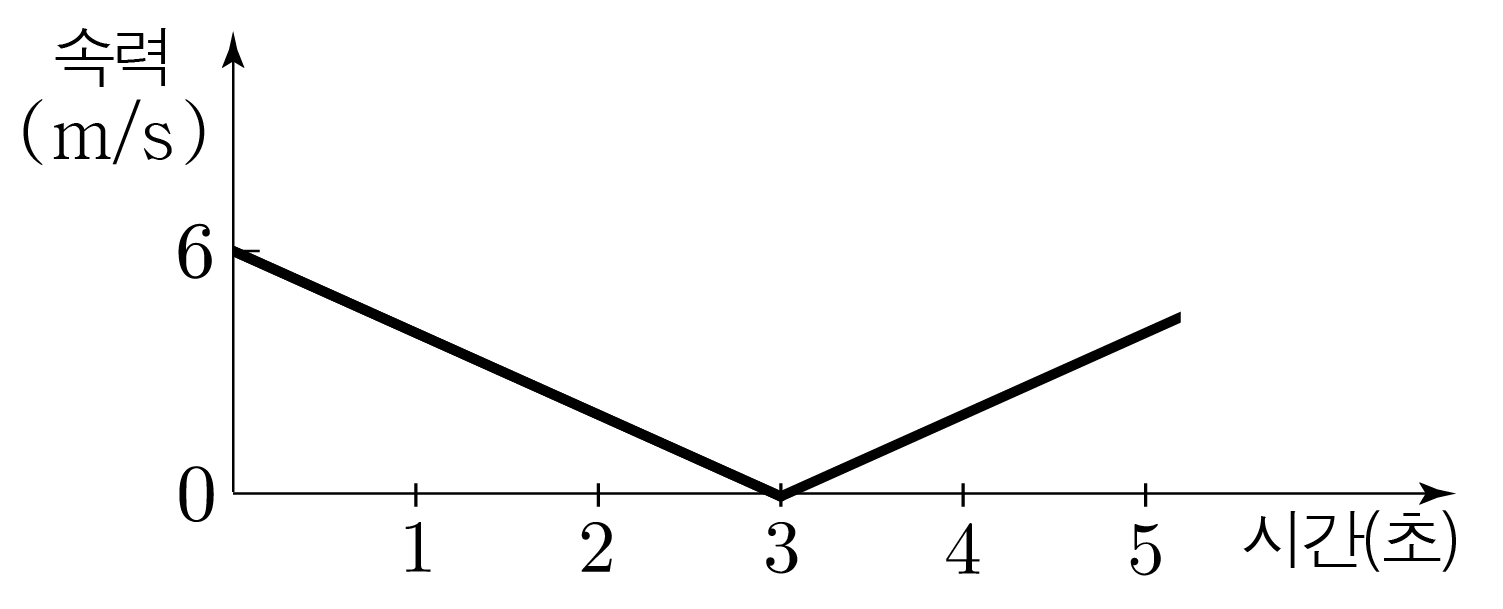
¶ 등가속도 운동하는 물체의 속력-시간 그래프 예시
축에 시간을, 축에 속력을 나타낸 그래프이다.
속도 대신 속력으로 나타내어 그래프로 물체의 운동 방향을 알 수 없다.
¶ 적용 문항
¶ 1번 문항

정답: $5$
ㄱ. 오른쪽 방향을 양, 자동차의 가속도를 라고 할 때, 문제에서 주어진 조건을 토대로 속도시간 그래프를 그리면 아래 그림과 같다.
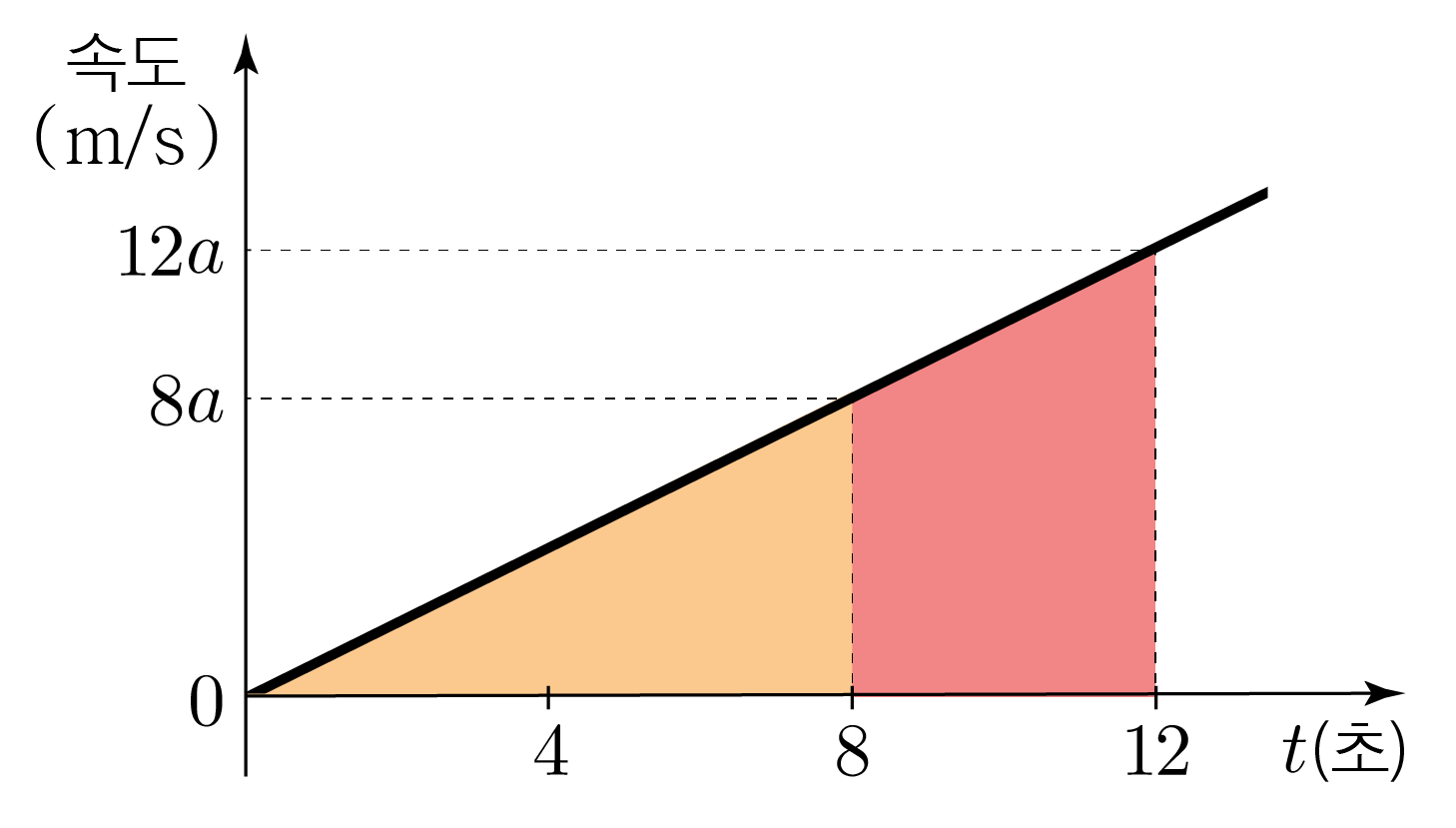
와 사이의 거리는 주황색과 분홍색 면적의 합과 같고, 이는 이므로
이다. (O)
ㄴ. 자동차가 를 통과할 때(일 때) 자동차의 속력은
이다. (O)
ㄷ. 와 사이의 거리는 분홍색 면적과 같으며, 부터 까지의 자동차의 평균 속도는
이다.
그러므로 와 사이의 거리는
이다. (O)
따라서 정답은 번이다.
¶ 2번 문항

정답: $4$
자동차가 를 통과한 후 를 통과하는데까지 걸린 시간을 , 오른쪽 방향을 양으로 하고, 문제에서 주어진 조건을 토대로 속도시간 그래프를 그리면 아래 그림과 같다.
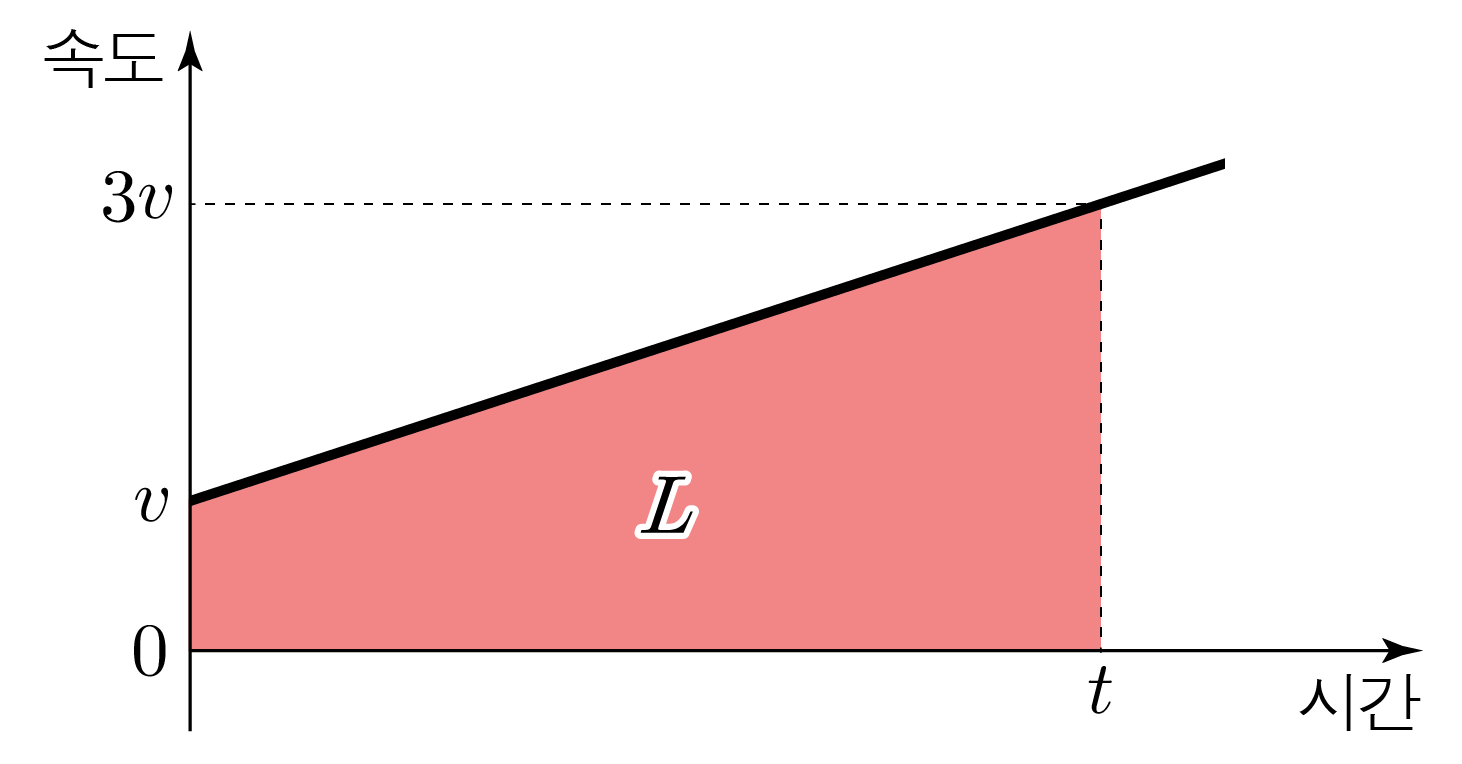
와 사이의 거리 은 분홍색 면적과 같고,
자동차가 를 통과한 순간부터 를 통과할 때까지의 평균 속도는 이므로
이다.
동안 자동차의 속도는 만큼 변하므로 자동차의 가속도의 크기는 이다.
이때 이므로 자동차의 가속도의 크기는 이다.
따라서 정답은 번이다.