¶ 지식 정보
¶ 전자 영역(입체수)
원자의 (결합수 비공유 전자쌍의 수)이다.
¶ 원자가 결합 이론
공유 결합은 한 원자의 오비탈과 다른 원자의 오비탈 사이의 겹침에 의해 형성된다는 이론이다.
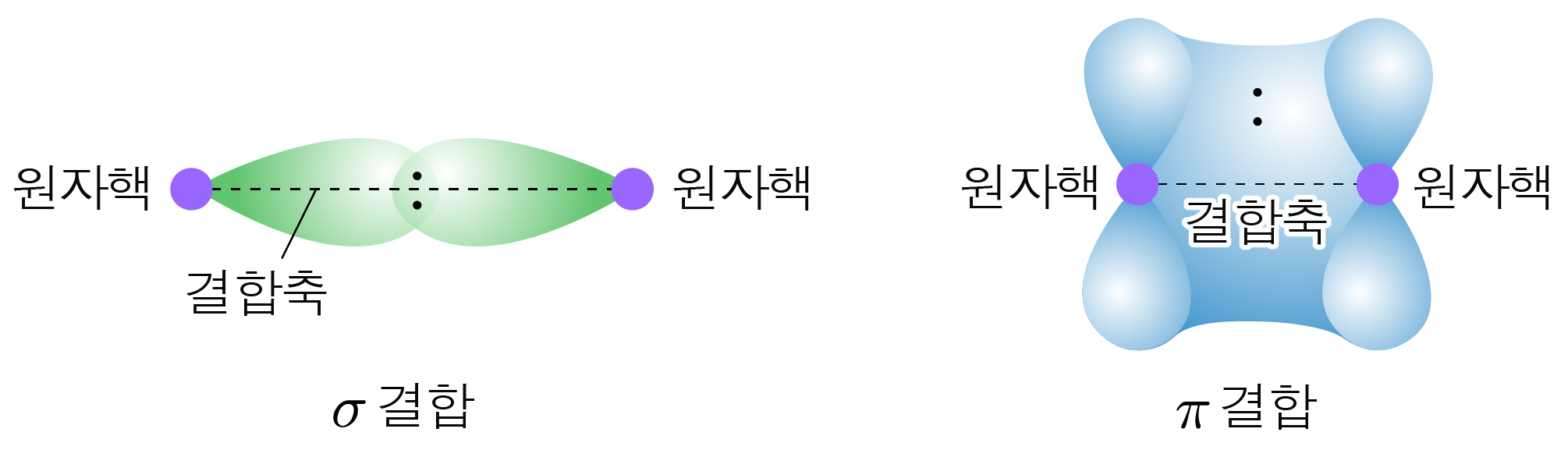
¶ σ 결합과 π 결합
- (시그마) 결합: 원자핵과 원자핵을 잇는 직선인 결합축을 따라 오비탈의 정면 중첩으로 형성되는 결합이다.
- (파이) 결합: 결합축에 수직으로 평행한 두 오비탈의 옆면 중첩으로 형성되는 결합이다.
단일 결합은 개의 결합으로,
중 결합은 개의 결합과 개의 결합,
중 결합은 개의 결합과 개의 결합으로 이루어진다.
아래 그림과 같이 결합에서는 한 원자가 회전하더라도 오비탈간 중첩이 유지되기 때문에 자유로운 회전이 가능하지만,
결합에서는 한 원자가 회전할 때 오비탈간 중첩이 유지되지 않으므로 회전이 제한된다.
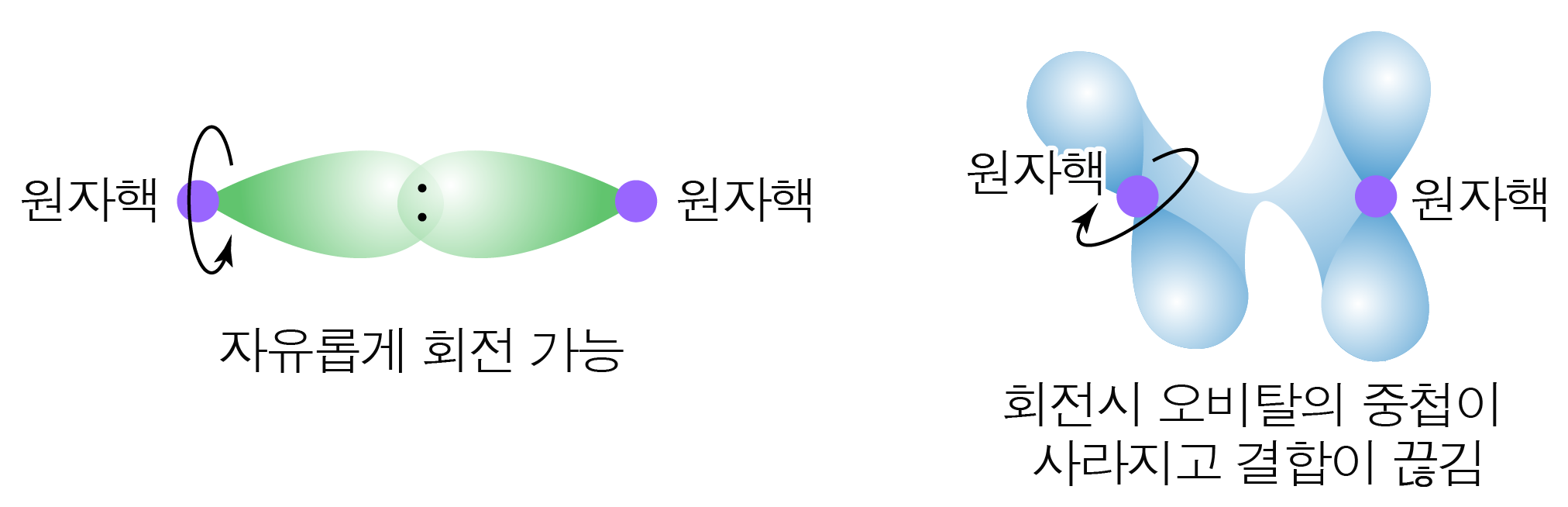
따라서 중 결합과 중 결합은 결합에 의해 회전이 제한된다.
¶ 혼성화
, 와 같은 오비탈이 혼합하여 새로운 형태와 에너지 준위의 오비탈(혼성 오비탈)을 만드는 것이다.
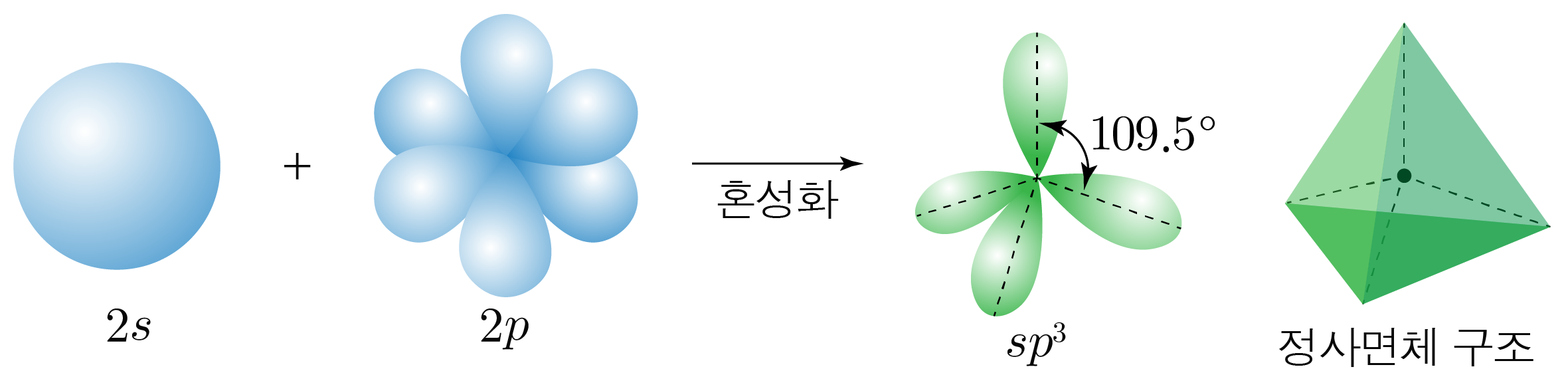
¶ 혼성 오비탈
개의 오비탈과 개의 오비탈이 혼합하여 만들어진 개의 동등한 혼성 오비탈이다.
원자가 개의 전자 영역을 가지는 경우에 해당한다.
혼성 오비탈은 정사면체 구조를 가지고, 혼성 오비탈 사이의 각은 이다.
핵심 혼성 오비탈만 표현하였다.
¶ 혼성 오비탈 예시
그림은 의 루이스 구조를 나타낸 것이다. 의 오비탈을 그려보자.
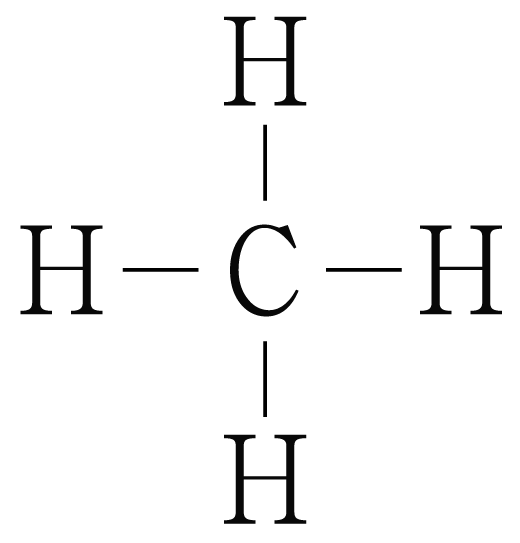
와 사이 결합은 단일 결합이므로 각 결합은 개의 결합으로 이루어진다.
원자는 개와 결합하고 있으므로 결합수는 개이고, 비공유 전자쌍은 개이다.
따라서 중심 원자의 전자 영역은 (결합수 비공유 전자쌍의 수) 개 개 개이다.
원자가 개의 전자 영역을 가지는 경우는 혼성 오비탈에 해당한다.
혼성 오비탈은 정사면체 구조를 가지고, 혼성 오비탈 사이의 각은 이므로 의 오비탈을 그리면 아래 그림과 같다.
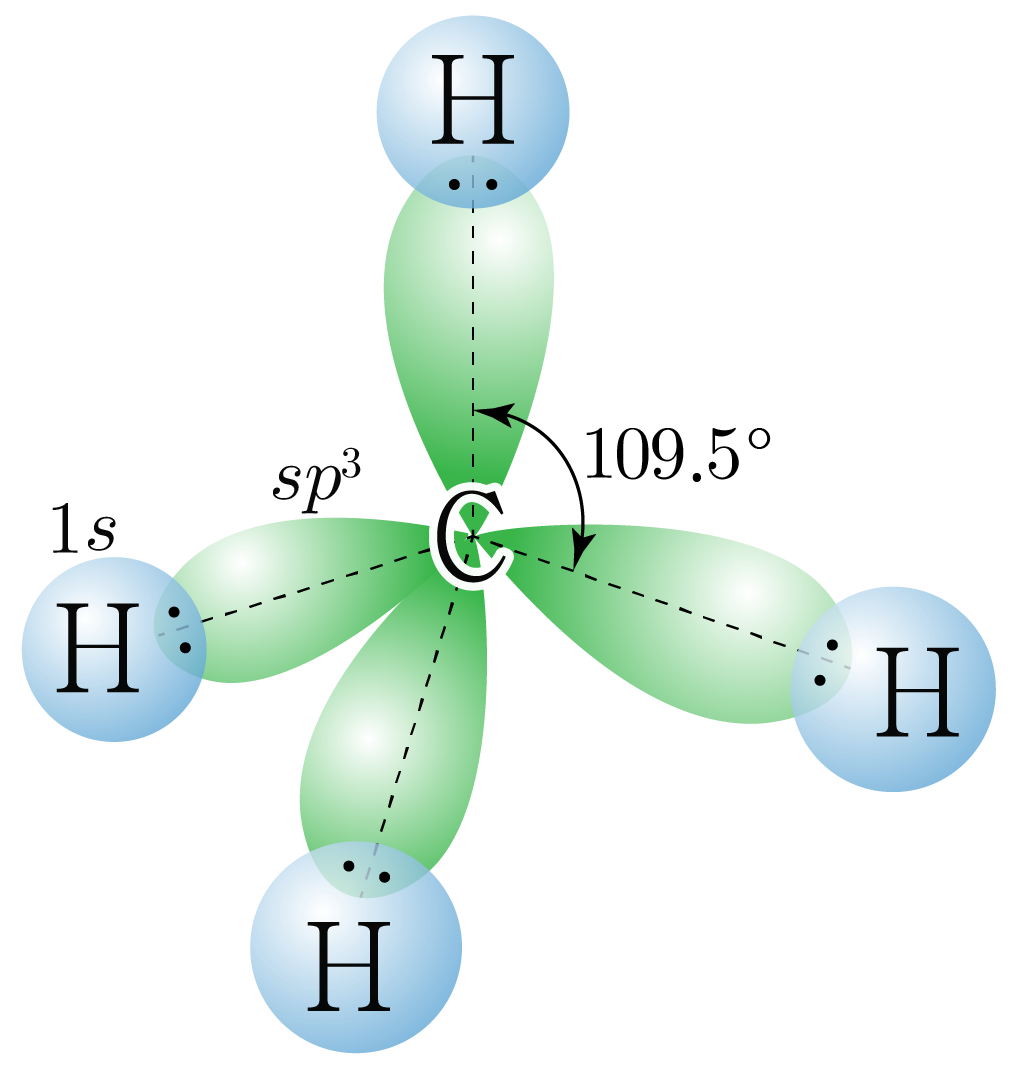
핵심 혼성 오비탈만 표현하였다.
¶ 혼성 오비탈
개의 오비탈과 개의 오비탈이 혼합하여 만들어진 개의 동등한 혼성 오비탈이다.
원자가 개의 전자 영역을 가지는 경우에 해당한다.
혼성 오비탈은 평면 삼각형 구조를 가지고, 혼성 오비탈 사이의 각은 이며,
혼성화에 참여하지 않은 오비탈과 수직을 이룬다.
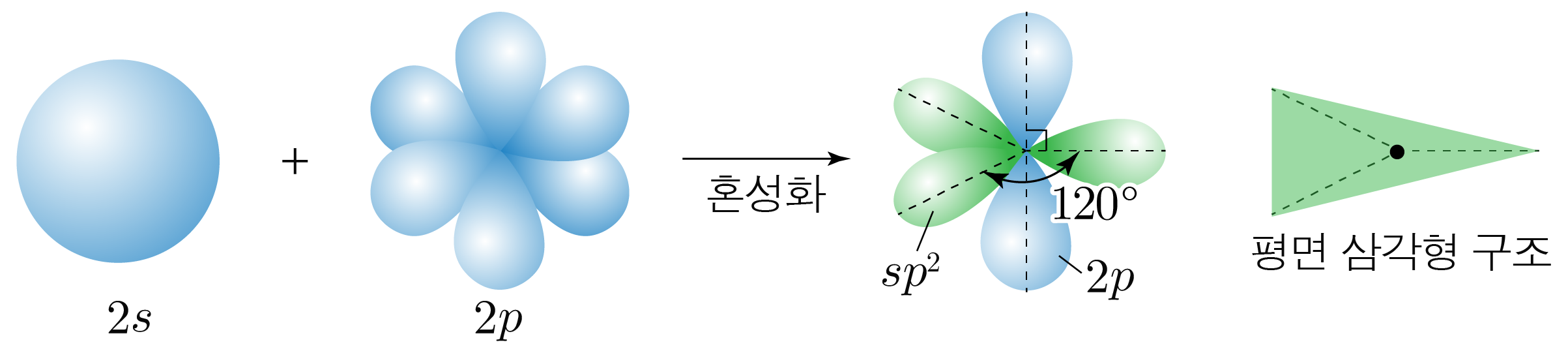
핵심 혼성 오비탈만 표현하였다.
¶ 혼성 오비탈 예시
그림은 의 루이스 구조를 나타낸 것이다. 의 오비탈을 그려보자.
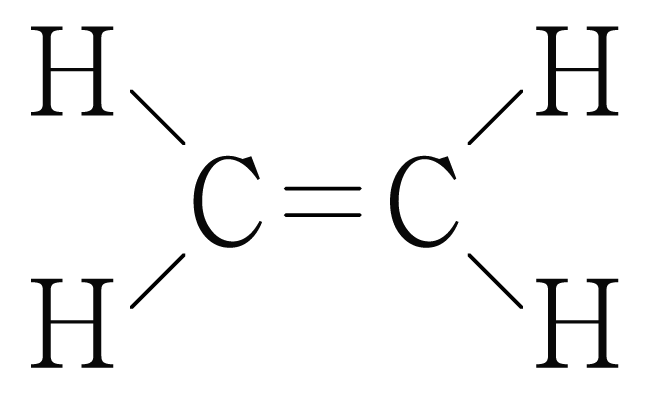
사이 결합은 중 결합이므로 개의 결합과 개의 결합으로 이루어진다.
각 원자는 개, 개와 결합하고 있으므로 결합수는 개이고, 비공유 전자쌍은 개이다.
따라서 각 원자의 전자 영역은 (결합수 비공유 전자쌍의 수) 개 개 개이다.
원자가 개의 전자 영역을 가지는 경우는 혼성 오비탈에 해당한다.
혼성 오비탈은 평면 삼각형 구조를 가지고, 혼성 오비탈 사이의 각은 이며,
혼성화에 참여하지 않은 오비탈과 수직을 이루므로 의 오비탈을 그리면 아래 그림과 같다.
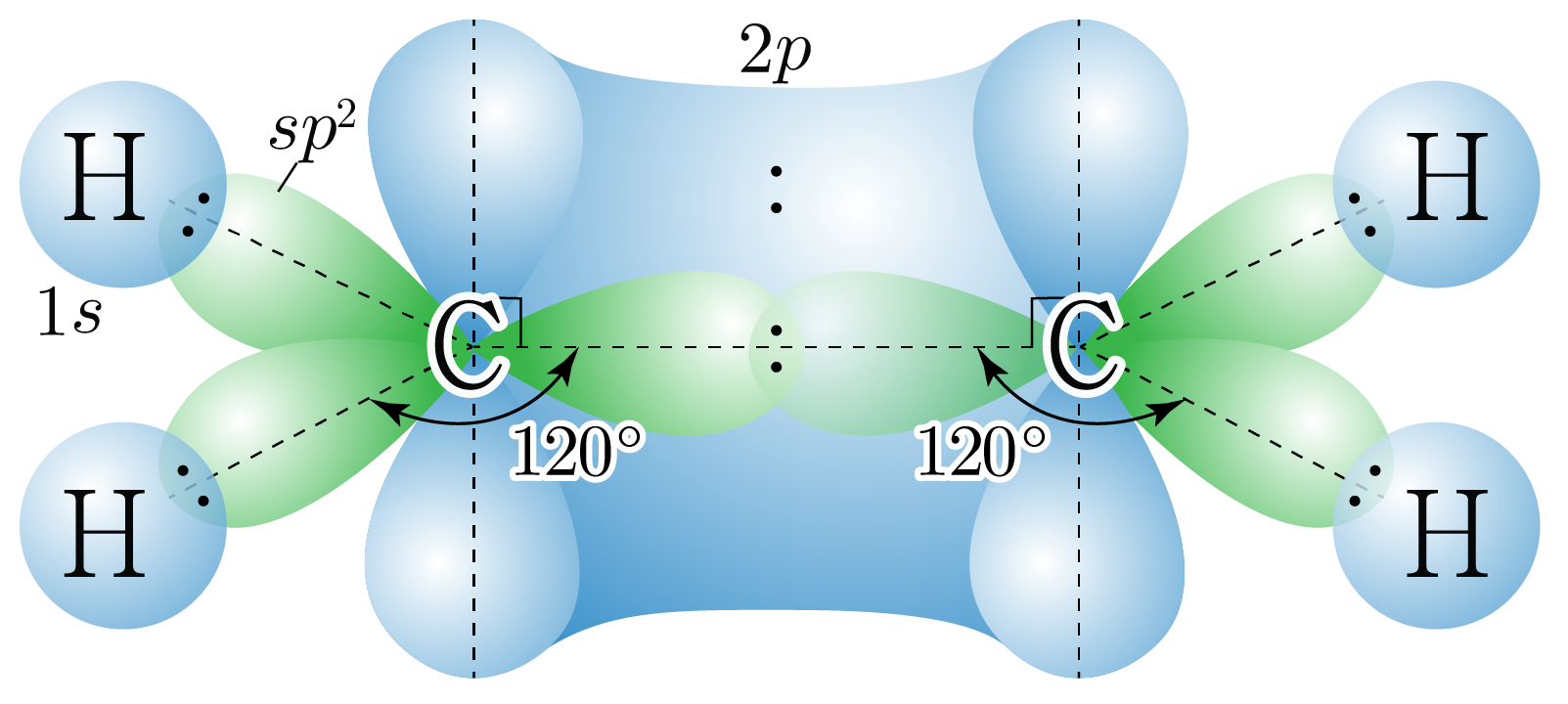
핵심 혼성 오비탈만 표현하였다.
¶ 혼성 오비탈
개의 오비탈과 개의 오비탈이 혼합하여 만들어진 개의 동등한 혼성 오비탈이다.
원자가 개의 전자 영역을 가지는 경우에 해당한다.
혼성 오비탈은 선형 구조를 가지고, 혼성 오비탈 사이의 각은 이며,
혼성화에 참여하지 않은 오비탈과 수직을 이룬다.
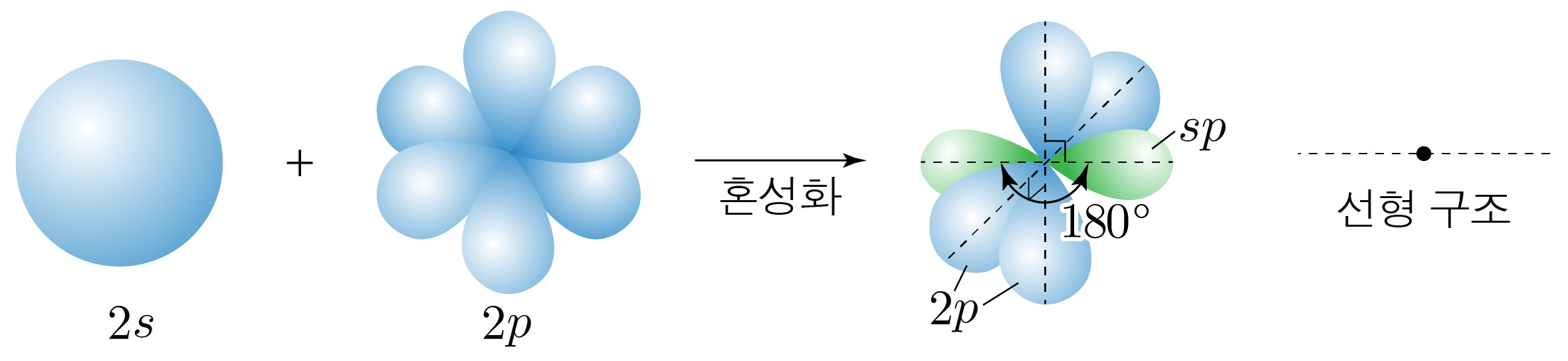
핵심 혼성 오비탈만 표현하였다.
¶ 혼성 오비탈 예시
그림은 의 루이스 구조를 나타낸 것이다. 의 오비탈을 그려보자.
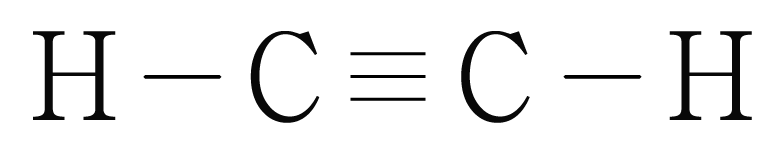
사이 결합은 중 결합이므로 개의 결합과 개의 결합으로 이루어진다.
각 원자는 개, 개와 결합하고 있으므로 결합수는 개이고, 비공유 전자쌍은 개이다.
따라서 각 원자의 전자 영역은 (결합수 비공유 전자쌍의 수) (개 개) 개이다.
원자가 개의 전자 영역을 가지는 경우는 혼성 오비탈에 해당한다.
혼성 오비탈은 선형 구조를 가지고, 혼성 오비탈 사이의 각은 이며,
혼성화에 참여하지 않은 오비탈과 수직을 이루므로 의 오비탈을 그리면 아래 그림과 같다.
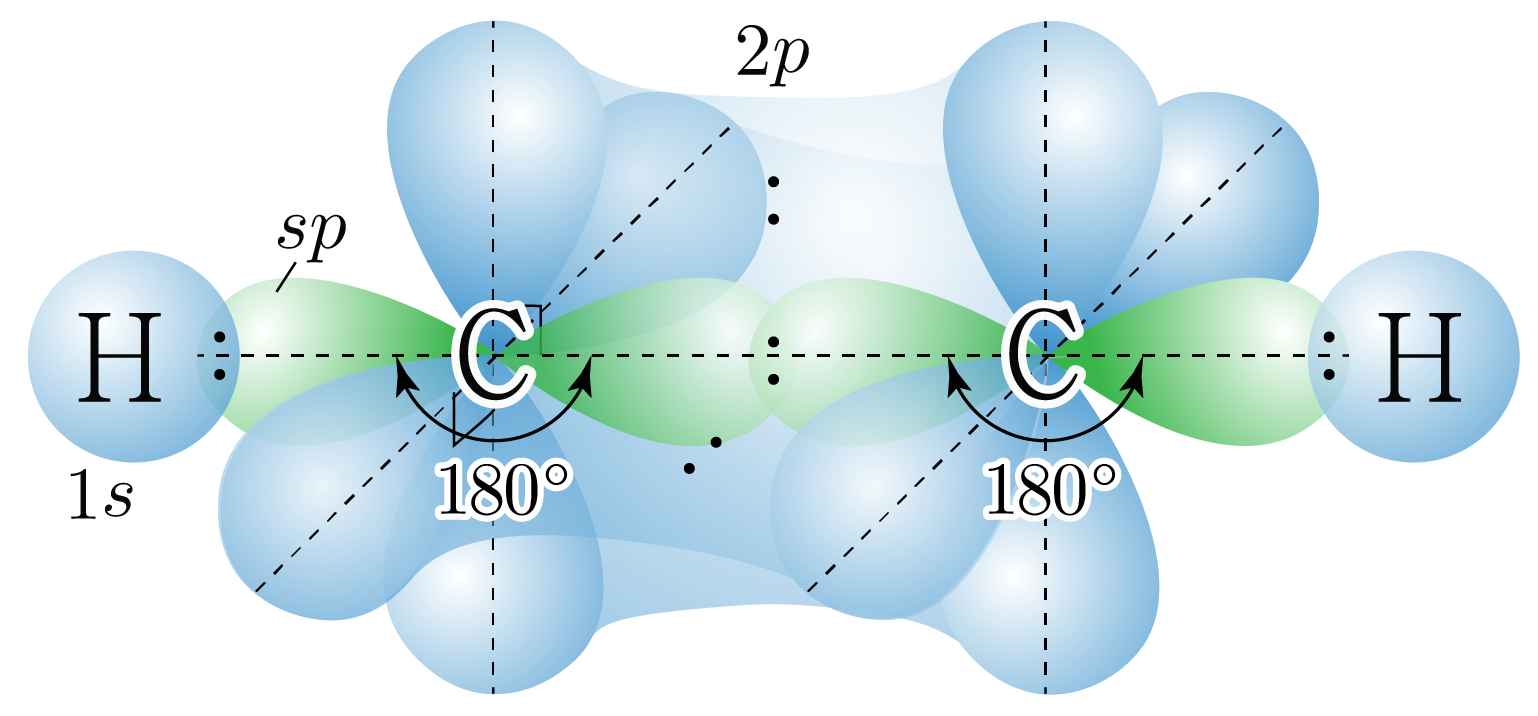
핵심 혼성 오비탈만 표현하였다.
¶ 오비탈의 기여도
각 혼성 오비탈별 오비탈과 오비탈의 기여도는 아래 표와 같다:
| 혼성 오비탈 | $s$ 오비탈의 기여도 | $p$ 오비탈의 기여도 |
|---|---|---|
| $sp^3$ | $\frac{1}{4}$ ($25\,\mathrm{\%}$) | $\frac{3}{4}$ ($75\,\mathrm{\%}$) |
| $sp^2$ | $\frac{1}{3}$ (약 $33.3\,\mathrm{\%}$) | $\frac{2}{3}$ (약 $66.7\,\mathrm{\%}$) |
| $sp$ | $\frac{1}{2}$ ($50\,\mathrm{\%}$) | $\frac{1}{2}$ ($50\,\mathrm{\%}$) |
오비탈의 기여도가 클수록 전자가 핵에 더 가까이 존재하여 공유 결합의 길이가 짧아진다.
¶ 적용 문항
¶ 1번 문항
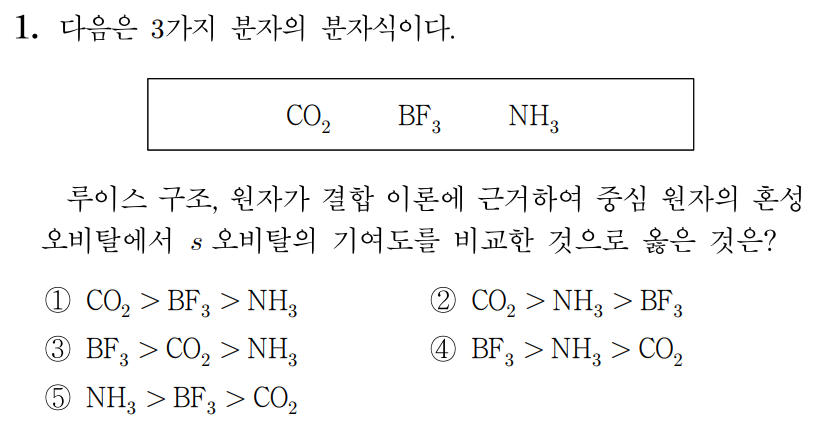
정답: $1$
, , 의 루이스 구조를 그리면 아래 그림과 같다.
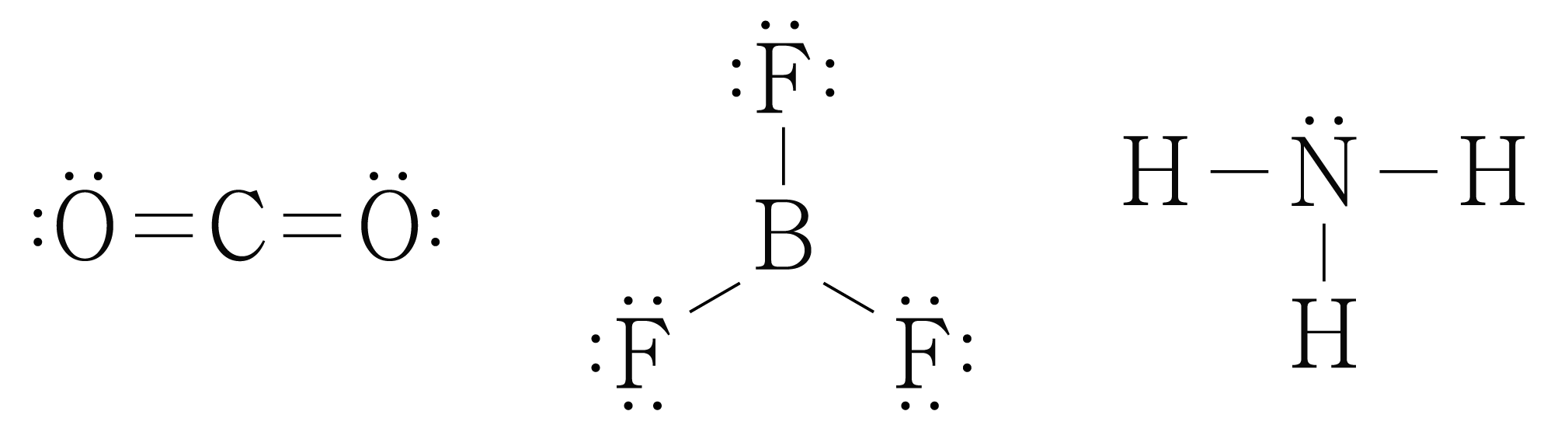
전자 영역은 원자의 (결합수 비공유 전자쌍의 수)이므로 각 분자에서 중심 원자의 전자 영역을 구하면 다음과 같다.
: (결합수 비공유 전자쌍의 수) (개 개) 개이다.
: (결합수 비공유 전자쌍의 수) (개 개) 개이다.
: (결합수 비공유 전자쌍의 수) (개 개) 개이다.
개, 개, 개의 전자 영역은 각각 , , 혼성 오비탈을 형성한 경우에 해당한다.
오비탈의 기여도는 이므로 , , 의 혼성 오비탈에서 오비탈의 기여도는
이다.
따라서 답은 번이다.
¶ 2번 문항

정답: $5$
ㄱ. 의 루이스 구조를 그리면 아래 그림과 같다.
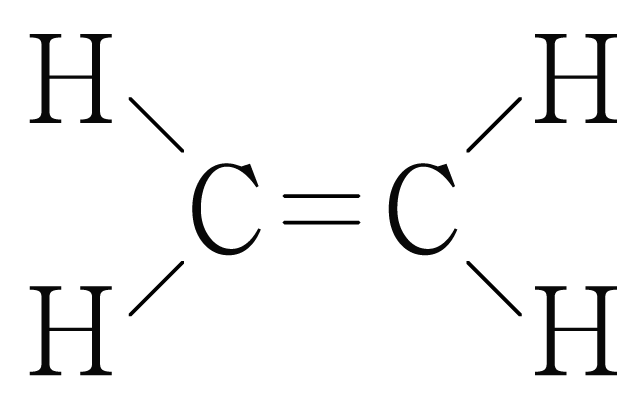
중 결합은 개의 결합과 개의 결합으로 이루어지므로
에서 두 탄소() 사이 결합에는 개의 결합과 개의 결합이 존재한다. (O)
ㄴ. 의 루이스 구조를 그리면 아래 그림과 같다.
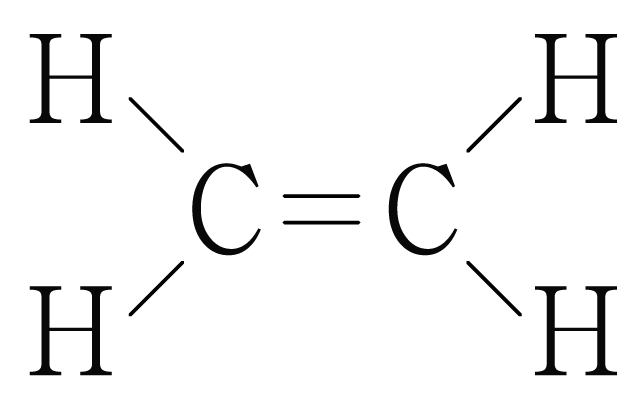
에서 각 탄소 원자(중심 원자)는 결합수는 개, 비공유 전자쌍은 개이므로 결합각은 이고, 선형 구조이다.
에서 각 탄소 원자(중심 원자)는 결합수는 개, 비공유 전자쌍은 개이므로 결합각은 이고, 평면 삼각형 구조이다.
그러므로 와 의 차원 구조를 그리면 아래 그림과 같다.
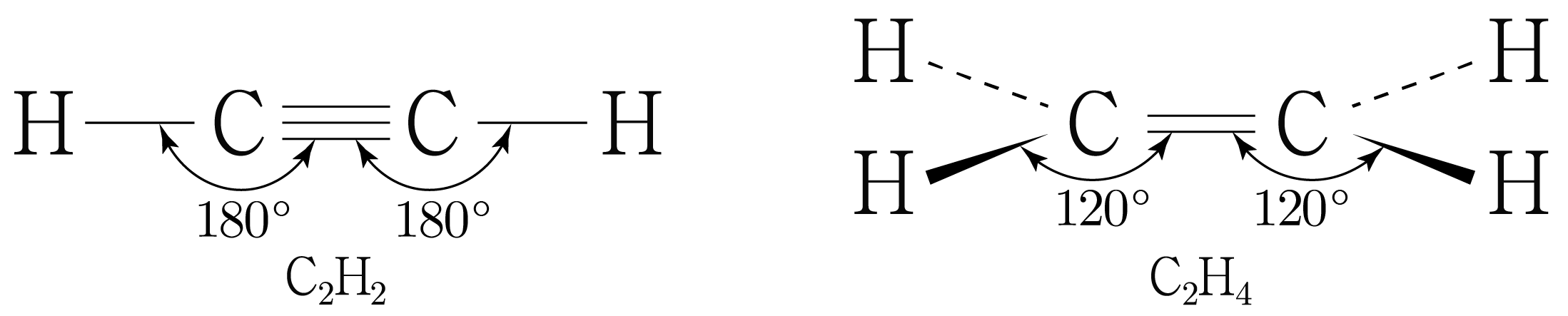
그러므로 평균 결합각은 가 보다 크다. (O)
ㄷ. 전자 영역은 원자의 (결합수 비공유 전자쌍의 수)이다.
에서 각 탄소 원자의 전자 영역은 (결합수 비공유 전자쌍의 수) (개 개) 개이고,
개의 전자 영역은 혼성 오비탈을 형성한 경우에 해당한다.
에서 각 탄소 원자의 전자 영역은 (결합수 비공유 전자쌍의 수) (개 개) 개이고,
개의 전자 영역은 혼성 오비탈을 형성한 경우에 해당한다.
오비탈의 기여도는 이므로 혼성 오비탈에서 오비탈의 기여도는 이다.
오비탈의 기여도가 클수록 전자가 핵에 더 가까이 존재하여 공유 결합의 길이는 짧아지므로
수소()와 탄소() 사이 평균 공유 결합의 길이는 가 보다 짧다. (O)
따라서 답은 번이다.

