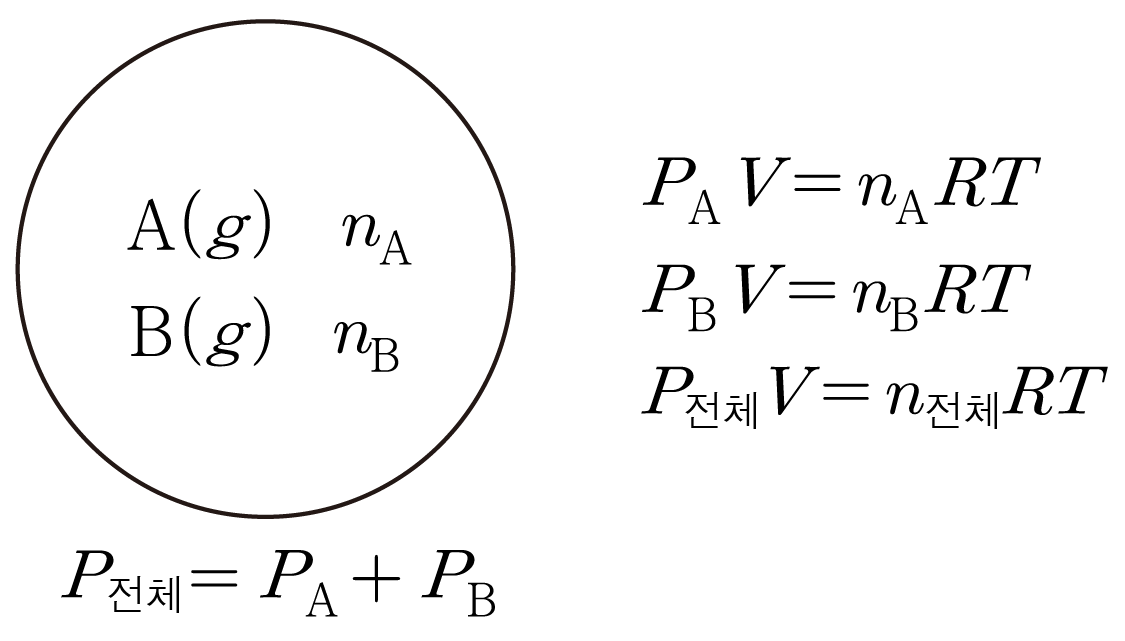혼합물에서 어떤 물질 A A X A X A n A n A n 전체 n 전체 X A = n A n 전체 X A = n 전체 n A
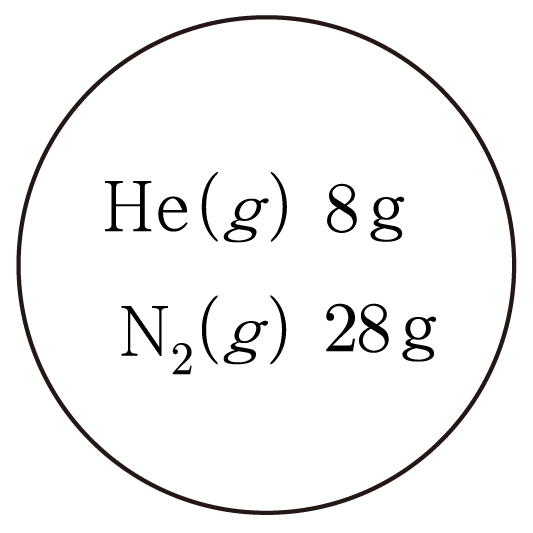
그림과 같이 강철 용기에 H e ( g ) H e ( g ) N 2 ( g ) N 2 ( g ) 8 g 8 g 28 g 2 8 g H e ( g ) H e ( g ) N 2 ( g ) N 2 ( g ) X H e X H e X N 2 X N 2 H e H e N N 4 4 14 1 4
H e ( g ) H e ( g ) 8 g 4 g / m o l = 2 4 g / m o l 8 g = 2
N 2 ( g ) N 2 ( g ) 28 g ( 14 × 2 ) g / m o l = 28 g 28 g / m o l = 1 ( 1 4 × 2 ) g / m o l 2 8 g = 2 8 g / m o l 2 8 g = 1
혼합물의 전체 몰 수 구하기:2 m o l + 1 m o l = 3 2 m o l + 1 m o l = 3
따라서 X H e = 2 m o l 3 m o l = 2 3 , X H e = 3 m o l 2 m o l = 3 2 , X N 2 = 1 m o l 3 m o l = 1 3 X N 2 = 3 m o l 1 m o l = 3 1
서로 다른 기체가 같은 용기 속에 혼합되어 있을 때, 각 성분 기체가 나타내는 압력이다.
혼합 기체의 전체 압력은 각 성분 기체의 부분 압력의 합과 같으며,
예를 들어 아래 그림과 같이 온도 T T A A B B A A B B P A P A P B P B n A n A n B n B P A V = n A R T , P A V = n A R T , P B V = n B R T P B V = n B R T P 전체 P 전체 P A + P B P A + P B
P 전체 P 전체 n 전체 = n A + n B n 전체 = n A + n B P 전체 V = n 전체 R T P 전체 V = n 전체 R T
A A X A X A P 전체 V = n 전체 R T P 전체 V = n 전체 R T R = P 전체 V n 전체 T R = n 전체 T P 전체 V P A V = n A R T P A V = n A R T R = P A V n A T R = n A T P A V P 전체 V n 전체 T = P A V n A T , n 전체 T P 전체 V = n A T P A V , P 전체 × n A n 전체 = P A P 전체 × n 전체 n A = P A
이때 n A n 전체 = X A n 전체 n A = X A P 전체 X A = P A P 전체 X A = P A
이를 통해 각 성분 기체의 부분 압력은 전체 압력과 몰 분율의 곱과 같음을 알 수 있다.
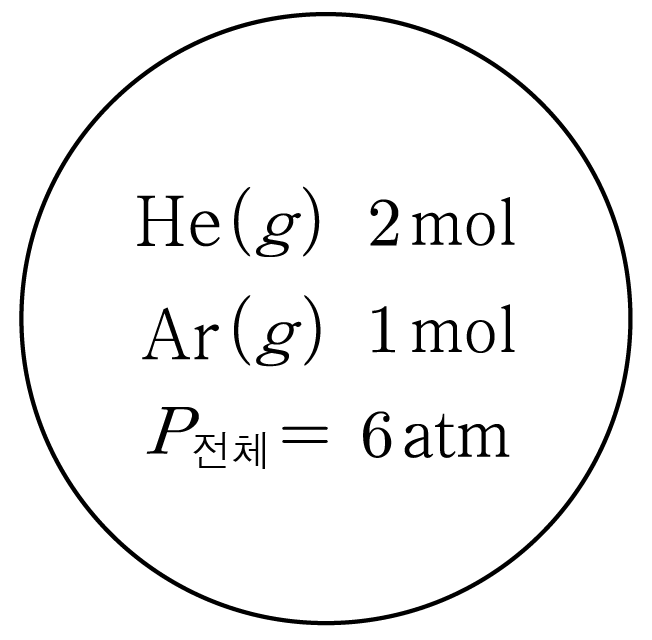
그림과 같이 온도 T T H e ( g ) H e ( g ) A r ( g ) A r ( g ) 2 m o l 2 m o l 1 m o l 1 m o l 6 a t m 6 a t m H e ( g ) H e ( g ) A r ( g ) A r ( g ) P H e P H e P A r P A r
혼합물의 전체 몰 수:2 m o l + 1 m o l = 3 2 m o l + 1 m o l = 3
H e ( g ) H e ( g ) 2 m o l 3 m o l = 2 3 3 m o l 2 m o l = 3 2 P H e = 6 a t m × 2 3 = 4 P H e = 6 a t m × 3 2 = 4
A r ( g ) A r ( g ) 1 m o l 3 m o l = 1 3 3 m o l 1 m o l = 3 1 P A r = 6 a t m × 1 3 = 2 P A r = 6 a t m × 3 1 = 2
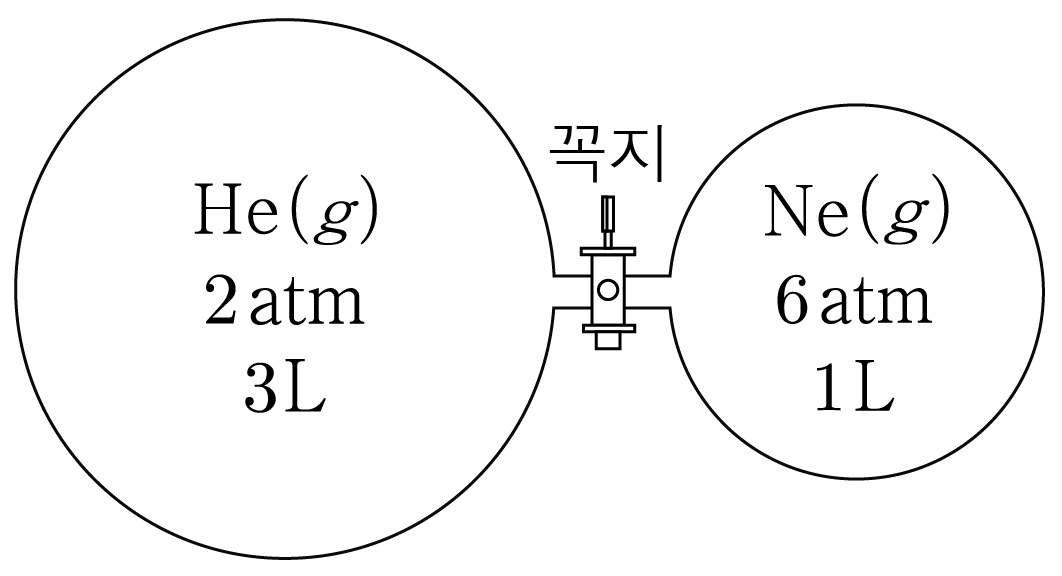
그림은 온도 T K T K H e ( g ) H e ( g ) N e ( g ) N e ( g ) H e ( g ) H e ( g ) N e ( g ) N e ( g )
H e ( g ) H e ( g ) N e ( g ) N e ( g ) n H e n H e n N e n N e R R 2 a t m × 3 L = n H e R × T K , 2 a t m × 3 L = n H e R × T K , n H e = 6 a t m ⋅ L R T K , n H e = R T K 6 a t m ⋅ L , 6 a t m × 1 L = n N e R × T K , 6 a t m × 1 L = n N e R × T K , n N e = 6 a t m ⋅ L R T K n N e = R T K 6 a t m ⋅ L n H e n H e n n n H e = n N e = n = 6 a t m ⋅ L R T K n H e = n N e = n = R T K 6 a t m ⋅ L
전체 압력을 먼저 구하고 이후 부분 압력 구하는 방법:
전체 몰 수는 2 n 2 n P 전체 P 전체 P 전체 × ( 3 L + 1 L ) = 2 n × R × T K P 전체 × ( 3 L + 1 L ) = 2 n × R × T K P 전체 × 4 L = 2 × 6 a t m ⋅ L R T K × R × T K , P 전체 × 4 L = 2 × R T K 6 a t m ⋅ L × R × T K , P 전체 × 4 L = 12 a t m ⋅ L , P 전체 × 4 L = 1 2 a t m ⋅ L , P 전체 = 3 a t m P 전체 = 3 a t m
H e ( g ) H e ( g ) n H e n 전체 = n 2 n = 1 2 n 전체 n H e = 2 n n = 2 1 H e ( g ) H e ( g ) 3 a t m × 1 2 = 3 2 a t m , 3 a t m × 2 1 = 2 3 a t m ,
N e ( g ) N e ( g ) n N e n 전체 = n 2 n = 1 2 n 전체 n N e = 2 n n = 2 1 N e ( g ) N e ( g ) 3 a t m × 1 2 = 3 2 a t m 3 a t m × 2 1 = 2 3 a t m
부분 압력을 먼저 구하고 이후 전체 압력 구하는 방법:
꼭지를 열고 충분한 시간이 흐른 후 H e ( g ) H e ( g ) N e ( g ) N e ( g ) P H e P H e P N e P N e
H e ( g ) H e ( g ) P H e × ( 3 L + 1 L ) = n H e R × T K P H e × ( 3 L + 1 L ) = n H e R × T K P H e × 4 L = 6 a t m ⋅ L R T K × R × T K , P H e × 4 L = R T K 6 a t m ⋅ L × R × T K , P H e × 4 L = 6 a t m ⋅ L , P H e × 4 L = 6 a t m ⋅ L , P H e = 3 2 P H e = 2 3
N e ( g ) N e ( g ) P N e × ( 3 L + 1 L ) = n N e R × T K P N e × ( 3 L + 1 L ) = n N e R × T K P N e × 4 L = 6 a t m ⋅ L R T K × R × T K , P N e × 4 L = R T K 6 a t m ⋅ L × R × T K , P N e × 4 L = 6 a t m ⋅ L , P N e × 4 L = 6 a t m ⋅ L , P N e = 3 2 P N e = 2 3
전체 압력(P 전체 P 전체 P 전체 = 3 2 a t m + 3 2 a t m = 3 a t m P 전체 = 2 3 a t m + 2 3 a t m = 3 a t m
1번 문항 정답 및 해설 보기
정답: $2$
H e H e 4 4 H e H e 4 g 4 g / m o l = 1 m o l 4 g / m o l 4 g = 1 m o l
N e N e 20 2 0 N e N e 25 g 20 g / m o l = 5 4 m o l 2 0 g / m o l 2 5 g = 4 5 m o l
그러므로 H e ( g ) H e ( g ) n H e n 전체 = 1 m o l 1 m o l + 5 4 m o l = 1 m o l 9 4 m o l = 4 9 n 전체 n H e = 1 m o l + 4 5 m o l 1 m o l = 4 9 m o l 1 m o l = 9 4
따라서 답은 2 2
2번 문항 정답 및 해설 보기
정답: $5$
N e ( g ) N e ( g ) A r ( g ) A r ( g ) n N e n N e n A r n A r R R 3 a t m × 2 L = n N e R T , 3 a t m × 2 L = n N e R T , 6 a t m ⋅ L = n N e R T , 6 a t m ⋅ L = n N e R T , n N e = 6 a t m ⋅ L R T , n N e = R T 6 a t m ⋅ L , 2 a t m × 1 L = n A r R × T , 2 a t m × 1 L = n A r R × T , 2 a t m ⋅ L = n A r R × T , 2 a t m ⋅ L = n A r R × T , n A r = 2 a t m ⋅ L R T n A r = R T 2 a t m ⋅ L
따라서 n A r = n = 2 a t m ⋅ L R T n A r = n = R T 2 a t m ⋅ L n N e = 3 n n N e = 3 n
ㄱ. 꼭지를 연 후 충분한 시간이 지났을 때, A r ( g ) A r ( g ) n n + 3 n = 1 4 n + 3 n n = 4 1
ㄴ. 혼합 기체의 전체 몰 수는 n + 3 n = 4 n n + 3 n = 4 n P 전체 P 전체 P 전체 × ( 2 L + 1 L ) = 4 n R T , P 전체 × ( 2 L + 1 L ) = 4 n R T , 3 P 전체 L = 4 n R T , 3 P 전체 L = 4 n R T , P 전체 = 4 n R T 3 L P 전체 = 3 L 4 n R T P 전체 = 4 n R T 3 L × 2 a t m ⋅ L R T = 8 3 a t m P 전체 = 3 L 4 n R T × R T 2 a t m ⋅ L = 3 8 a t m
ㄷ. N e ( g ) N e ( g ) 3 n n + 3 n = 3 4 n + 3 n 3 n = 4 3 N e ( g ) N e ( g ) 8 3 a t m × 3 4 = 2 a t m 3 8 a t m × 4 3 = 2 a t m
따라서 답은 5 5