¶ 지식 정보
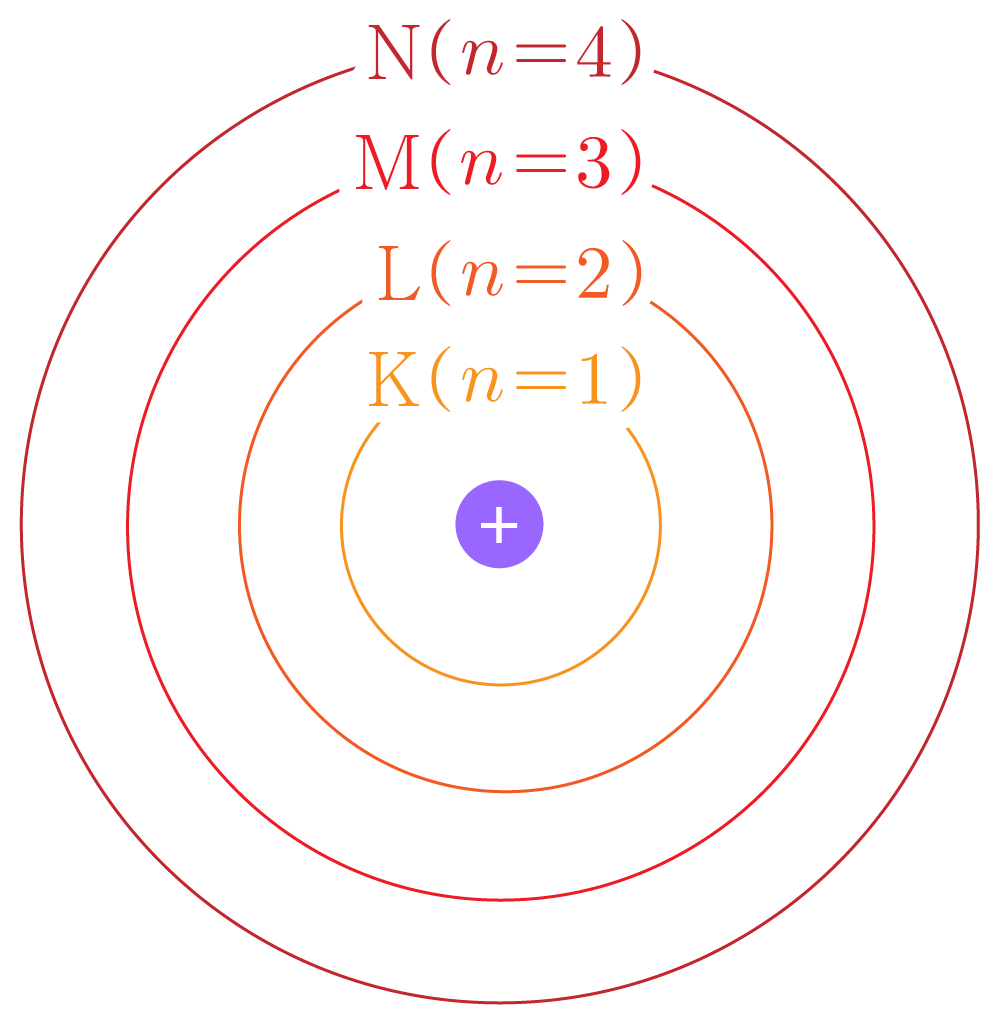
¶ 전자 껍질의 이름
주 양자수 이 인 껍질은
주 양자수 이 인 껍질은
주 양자수 이 인 껍질은
주 양자수 이 인 껍질은 으로 나타낸다.
¶ 오비탈(궤도 함수)
전자가 원자핵 주위에서 발견될 확률을 나타내는 함수이다. 오비탈의 종류는 등이 있다.
오비탈의 모양은 전자가 발견될 확률이 이상인 공간을 경계면으로 나타낸 것이다.
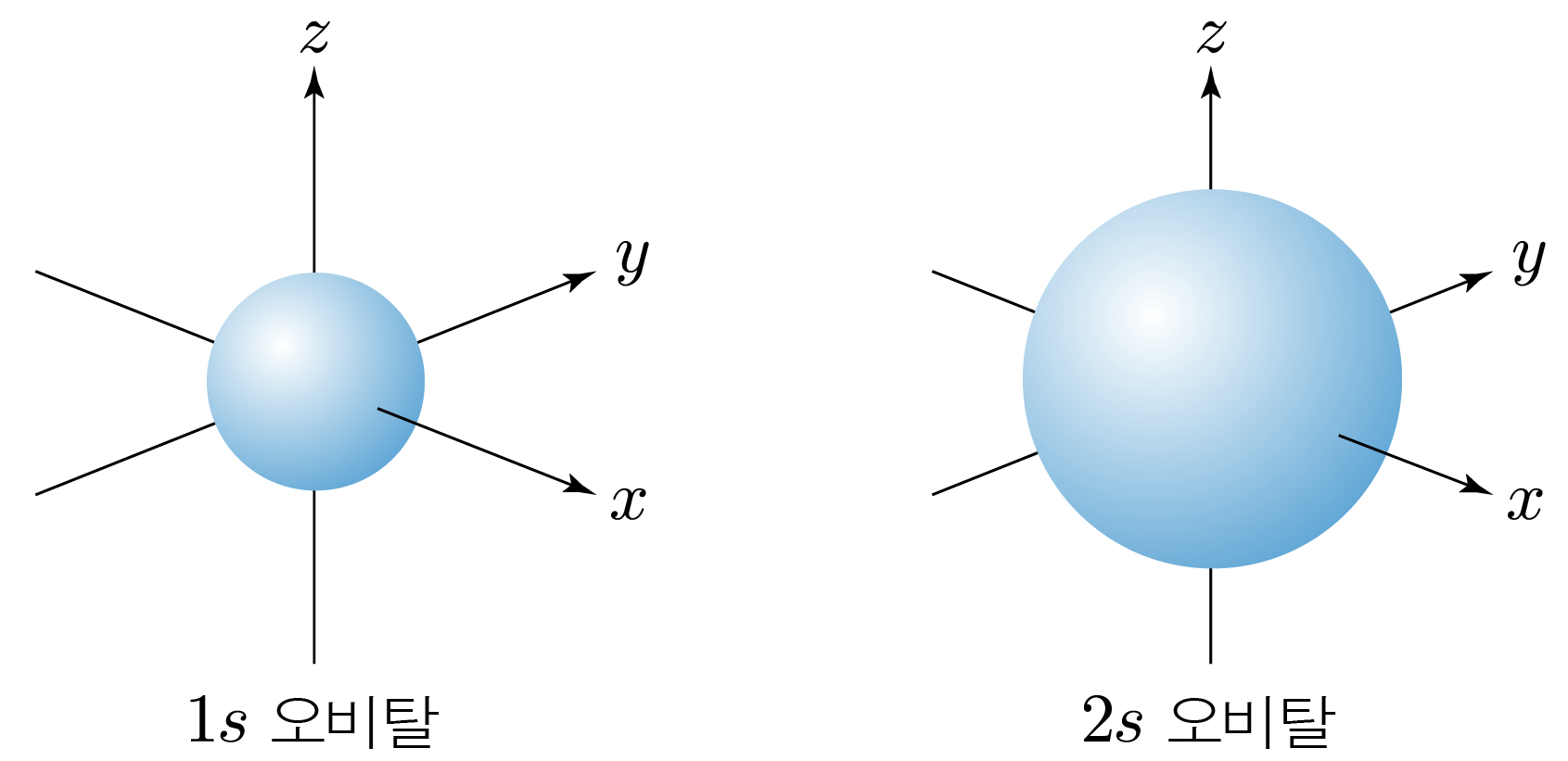
¶ s 오비탈의 특징
- 구형 모양의 개의 오비탈로 이루어진다.
- 구형이기 때문에 방향성이 없다.
방향에 관계없이 원자핵으로부터 거리가 같으면 전자가 발견될 확률도 같다. - 주 양자수 이 클수록 오비탈의 크기가 크다.
- 모든 마다 존재한다.
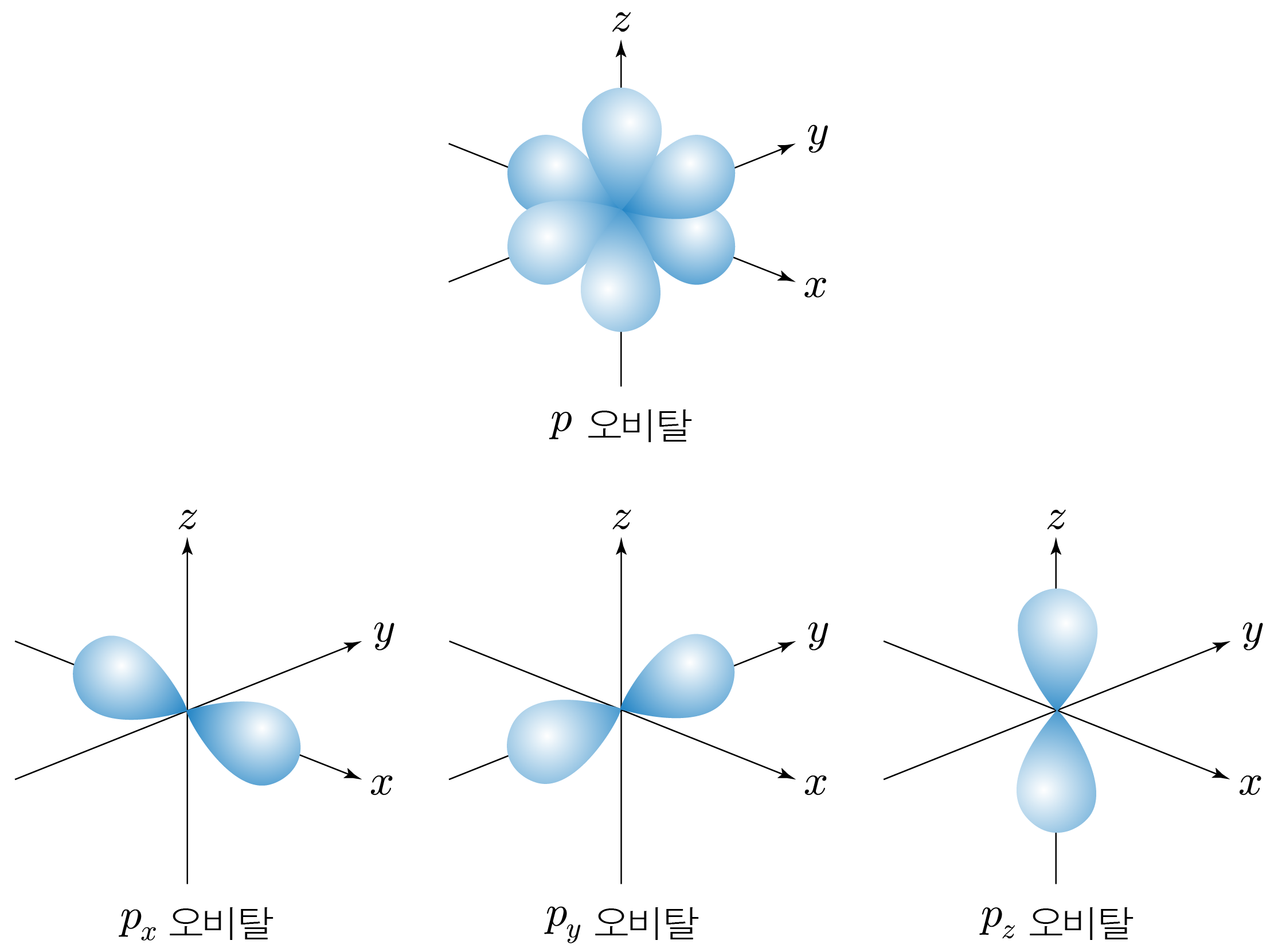
¶ p 오비탈의 특징
- 아령 모양의 개의 오비탈로 이루어진다.
- 방향성이 있으며, 차원 공간의 각 축 방향으로 분포한다.
- 축 방향으로 분포하는 오비탈은 각각 로 나타낸다.
- 주 양자수 이상부터 존재한다.
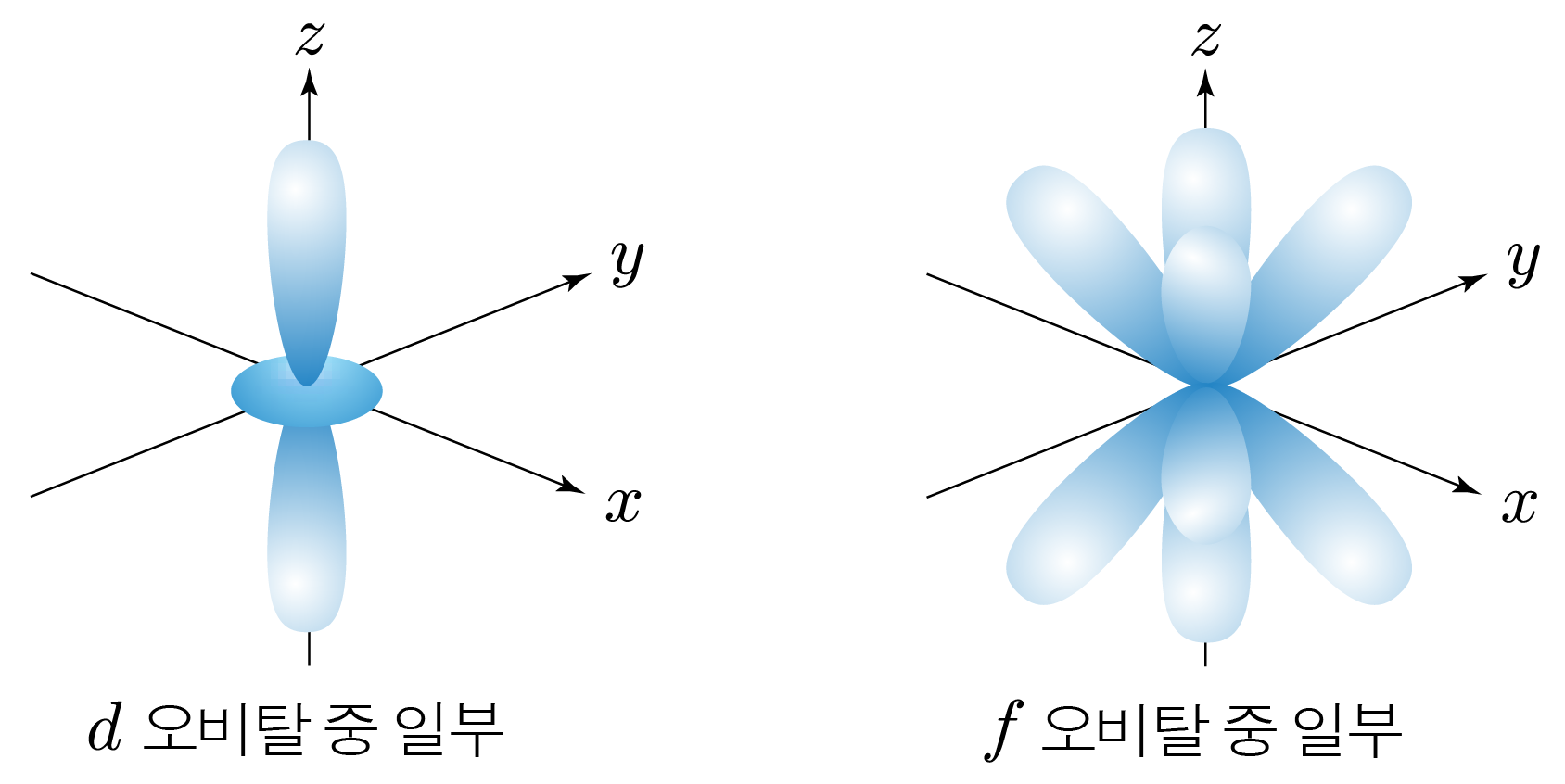
¶ d와 f 오비탈의 특징
- 네잎클로버나 도넛 등 복잡한 모양의 오비탈이다.
- 는 개, 는 개의 오비탈로 이루어진다.
- 오비탈은 주 양자수 이상부터, 오비탈은 이상부터 존재한다.
¶ 오비탈에 들어갈 수 있는 전자의 수
오비탈 개당 전자는 최대 개까지 들어갈 수 있다.
오비탈의 개수가 개인 오비탈은 최대 개,
오비탈의 개수가 개인 오비탈은 최대 개( 각각 개씩),
오비탈의 개수가 개인 오비탈은 최대 개,
오비탈의 개수가 개인 오비탈은 최대 개의 전자가 들어갈 수 있다.
¶ 오비탈의 표기
주 양자수를 표기하는 경우 오비탈의 종류( )의 왼쪽에 표기한다.
오비탈에 들어있는 전자의 개수를 표기하는 경우 오비탈의 종류의 오른쪽 위에 표기한다.

$n$에 주 양자수를, $\mathrm{X}$에 오비탈의 종류를 표기한다.
예를 들어, 주 양자수()가 인 오비탈에 전자가 개 들어있으면 로 표기한다.
¶ 전자 껍질별 오비탈 정리
| 전자 껍질 | $\mathrm{K}$ | $\mathrm{L}$ | $\mathrm{M}$ | $\mathrm{N}$ | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 주 양자수$(n)$ | $1$ | $2$ | $3$ | $4$ | ||||||
| 오비탈 종류 | $1s$ | $2s$ | $2p$ | $3s$ | $3p$ | $3d$ | $4s$ | $4p$ | $4d$ | $4f$ |
| 오비탈 수 | $1$ | $1$ | $3$ | $1$ | $3$ | $5$ | $1$ | $3$ | $5$ | $7$ |
| 최대로 들어갈 수 있는 전자의 수 |
$2$ | $2$ | $6$ | $2$ | $6$ | $10$ | $2$ | $6$ | $10$ | $14$ |
¶ 적용 문항
¶ 1번 문항
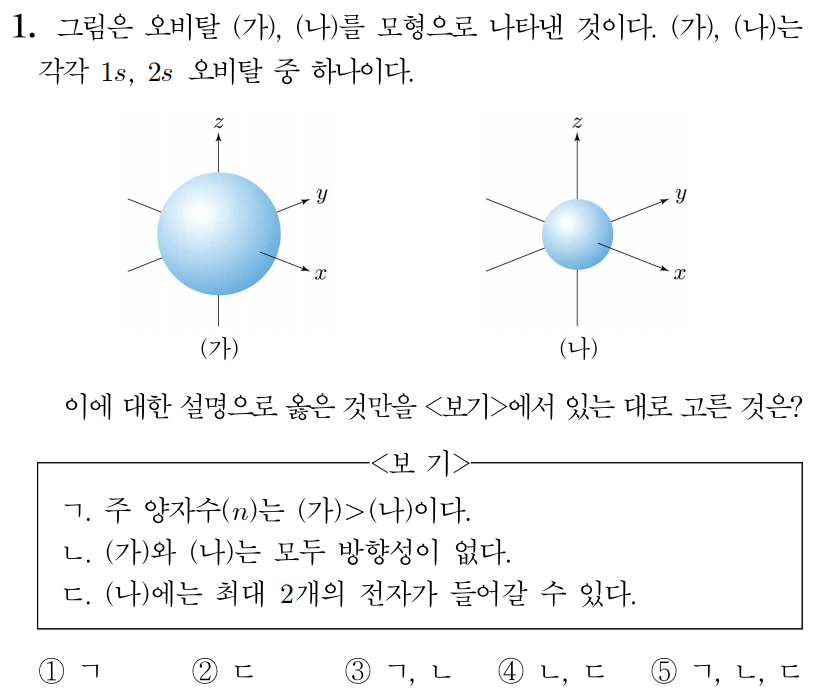
정답: $5$
ㄱ. 주 양자수는 오비탈의 종류( )의 왼쪽에 표기하고,
주 양자수 이 클수록 오비탈의 크기가 크므로 (가), (나)는 각각 이다.
그러므로 주 양자수()는 (가)(나)이다. (O)
ㄴ. 오비탈은 방향성이 없으므로 (가)와 (나)는 모두 방향성이 없다. (O)
ㄷ. 오비탈은 전자가 최대 개 들어가므로 (나)에는 최대 개의 전자가 들어갈 수 있다. (O)
따라서 답은 번이다.
¶ 2번 문항

정답: $3$
ㄱ. 그림의 오비탈은 아령 모양이므로 오비탈이다. (O)
ㄴ. 주 양자수는 오비탈의 종류( )의 왼쪽에 표기하므로 주 양자수()는 이다. (O)
ㄷ. 전자는 에 각각 최대 개씩 들어갈 수 있다. (X)
따라서 답은 번이다.


