¶ 지식 정보
| 해당 지식 | |
|---|---|
|
|
| 하위 지식 | 상위 지식 |
|
|
¶ 사칙 계산 순서
사칙 계산의 순서는 다음과 같은 규칙을 따른다.
우선 순위가 높은 수식부터 먼저 계산하며, 우선 순위는 아래와 같다.
괄호 안의 수식
곱셈과 나눗셈
덧셈과 뺄셈
우선 순위가 같은 경우 왼쪽에서 오른쪽으로 차례대로 계산한다.
¶ 사칙 계산 순서 예시
- 우선 순위가 같은 경우:
를 계산해보자.
덧셈과 뺄셈의 우선 순위는 같으므로 왼쪽에서 오른쪽으로 차례대로 계산한다.
따라서 이다.
- 우선 순위가 다른 경우:
를 계산해보자.
곱셈과 나눗셈은 덧셈과 뺄셈보다 우선 순위가 높으므로 먼저 계산한다.
따라서 이다.
- 괄호가 있는 경우:
을 계산해보자.
곱셈과 나눗셈은 덧셈과 뺄셈보다 우선 순위가 높지만, 괄호 안의 수식이 가장 높은 우선 순위를 가지므로 가장 먼저 계산한다.
따라서 이다.
- 괄호 안에 우선 순위가 다른 수식이 있는 경우:
을 계산해보자.
괄호 안의 수식이 가장 높은 우선 순위를 가지므로 가장 먼저 계산한다.
이때 괄호 안의 수식 에서 곱셈과 나눗셈은 덧셈과 뺄셈보다 우선 순위가 높으므로 먼저 계산한다.
따라서 이다.
¶ 적용 문항
¶ 1번 문항
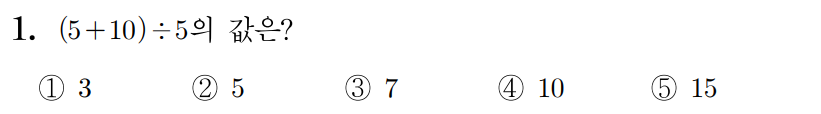
정답: $1$
곱셈과 나눗셈은 덧셈과 뺄셈보다 우선 순위가 높지만, 괄호 안의 수식이 가장 높은 우선 순위를 가지므로 가장 먼저 계산한다.
그러므로 이다.
따라서 정답은 번이다.
¶ 2번 문항
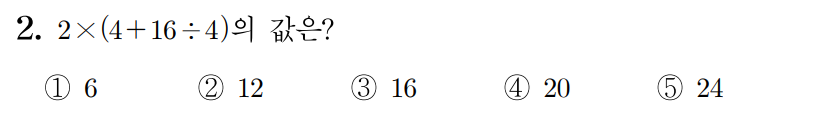
정답: $3$
괄호 안의 수식이 가장 높은 우선 순위를 가지므로 가장 먼저 계산한다. 이때 괄호 안의 수식 에서 곱셈과 나눗셈은 덧셈과 뺄셈보다 우선 순위가 높으므로 먼저 계산한다.
그러므로 이다.
따라서 정답은 번이다.