전하 사이에 작용하는 힘이다.
전하량의 부호가 같은 두 전하 사이에는 서로 밀어내는 힘인 척력이 작용하고,
전하를 띠며 크기를 가지지 않는 이상적인 물체이다.
두 점전하 사이에 작용하는 전기력의 크기는 두 점전하의 전하량 크기의 곱에 비례하고,
이 관계에서 비례 상수를 쿨롱 상수라고 한다. (진공에서 쿨롱 상수 값은 8.99 × 1 0 9 N ⋅ m 2 / C 2 8 . 9 9 × 1 0 9 N ⋅ m 2 / C 2
전기력의 크기를 F 전기 F 전기 k k q 1 q 1 q 2 q 2 d d F 전기 = k q 1 q 2 d 2 F 전기 = k d 2 q 1 q 2
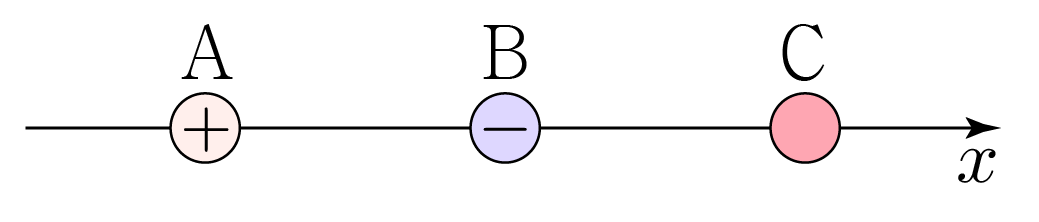
그림과 같이 x x A A B B C C A A B B + + − − A A 0 0 C C B B C C
인접한 점전하 사이의 거리를 d d k k A A B B C C q A q A q B q B q C q C A A B B k q A q B d 2 k d 2 q A q B A A C C k q A q C ( 2 d ) 2 = k q A q C 4 d 2 k ( 2 d ) 2 q A q C = k 4 d 2 q A q C
전하량의 부호가 같은 두 전하 사이에는 척력이 작용하고,B B A A + x + x
이때 A A 0 0 B B A A C C A A
이를 통해 C C A A B B A A − x − x A A C C C C + +
또한 B B A A C C A A k q A q B d 2 = k q A q C 4 d 2 , k d 2 q A q B = k 4 d 2 q A q C , q A q B d 2 = q A q C 4 d 2 , d 2 q A q B = 4 d 2 q A q C , 4 q A q B = q A q C , 4 q A q B = q A q C , q C = 4 q B q C = 4 q B
1번 문항 정답 및 해설 보기
정답: $4$
A A P P B B q q C C Q Q k k d d + x + x + + A A P P + k q 2 d 2 + k d 2 q 2 B B P P + k q 2 d 2 + k d 2 q 2 P P + x + x
이때 P P 0 0 C C P P − x − x
P P C C C C + + C C P P − k q Q ( 2 d ) 2 = − k q Q 4 d 2 − k ( 2 d ) 2 q Q = − k 4 d 2 q Q
P P 0 0 + k q 2 d 2 + k q 2 d 2 − k q Q 4 d 2 = 0 , + k d 2 q 2 + k d 2 q 2 − k 4 d 2 q Q = 0 , k 2 q 2 d 2 − k q Q 4 d 2 = 0 , k d 2 2 q 2 − k 4 d 2 q Q = 0 , 2 q 2 d 2 − q Q 4 d 2 = 0 , d 2 2 q 2 − 4 d 2 q Q = 0 , 2 q 2 − q Q 4 = 0 , 2 q 2 − 4 q Q = 0 , 2 q 2 = q Q 4 , 2 q 2 = 4 q Q , 8 q 2 = q Q , 8 q 2 = q Q , Q = 8 q Q = 8 q
이를 통해 C C A A 8 8
따라서 정답은 4 4
2번 문항 정답 및 해설 보기
정답: $5$
ㄱ. A A B B A A B B B B A A + x + x
이때 A A B B C C A A − x − x C C + + A A − x − x
ㄴ. 쿨롱 상수를 k k d d + x + x + +
A A C C + k ( 2 q ) × ( 8 q ) ( 2 d ) 2 = k 16 q 2 4 d 2 = k 4 q 2 d 2 + k ( 2 d ) 2 ( 2 q ) × ( 8 q ) = k 4 d 2 1 6 q 2 = k d 2 4 q 2
B B C C − k q × ( 8 q ) d 2 = − k 8 q 2 d 2 − k d 2 q × ( 8 q ) = − k d 2 8 q 2
C C k 4 q 2 d 2 − k 8 q 2 d 2 = − k 4 q 2 d 2 k d 2 4 q 2 − k d 2 8 q 2 = − k d 2 4 q 2
C C − − C C − x − x
ㄷ. C C A A − k ( 2 q ) × ( 8 q ) ( 2 d ) 2 = − k 16 q 2 4 d 2 = − k 4 q 2 d 2 − k ( 2 d ) 2 ( 2 q ) × ( 8 q ) = − k 4 d 2 1 6 q 2 = − k d 2 4 q 2
B B A A + k q × ( 2 q ) d 2 = k 2 q 2 d 2 + k d 2 q × ( 2 q ) = k d 2 2 q 2
F = ∣ − k 4 q 2 d 2 + k 2 q 2 d 2 ∣ , F = ∣ ∣ ∣ ∣ − k d 2 4 q 2 + k d 2 2 q 2 ∣ ∣ ∣ ∣ , F = ∣ − k 2 q 2 d 2 ∣ , F = ∣ ∣ ∣ ∣ − k d 2 2 q 2 ∣ ∣ ∣ ∣ , F = k 2 q 2 d 2 F = k d 2 2 q 2
그러므로 C C ∣ − k 4 q 2 d 2 ∣ = k 4 q 2 d 2 = 2 F ∣ ∣ ∣ ∣ − k d 2 4 q 2 ∣ ∣ ∣ ∣ = k d 2 4 q 2 = 2 F
따라서 정답은 5 5