¶ 지식 정보
¶ 대조군과 실험군
대조군은 실험에서 비교의 기준이 되어, 아무 변화도 주지 않고 그대로 둔 집단이고, 실험군은 검증하려는 요인을 변화시킨 집단이다.
대조군과 실험군을 활용한 실험을 대조 실험이라 한다.
¶ 변인
실험에서 변화를 줄 수 있는 요인이다.
변인에는 크게 독립 변인(통제 변인, 조작 변인)과 종속 변인이 있다.
¶ 독립 변인
실험 결과에 영향을 줄 수 있는 변인으로, 통제 변인과 조작 변인이 있다.
- 통제 변인: 실험에서 일정하게 유지시키는 독립 변인
- 조작 변인: 실험에서 의도적으로 변화시키는 독립 변인
¶ 종속 변인
조작 변인에 의해 변하는 변인이다.
¶ 변인 통제
대조 실험에서 조작 변인을 제외한 다른 모든 독립 변인을 일정하게 유지하는 것이다.
¶ 생명과학에서의 그래프
실험 결과나 생명 현상에서 얻은 데이터의 변화를 그림으로 나타낸 것이다.
¶ 생명과학 실험 결과 그래프에서 축별 의미
가로축은 조작 변인을 나타내고, 세로축은 종속 변인을 나타낸다.
¶ 생명과학 실험 결과 그래프에서 축별 의미 예시
그림은 어느 생명과학 실험 결과를 나타낸 것이다. 이를 해석해보자.
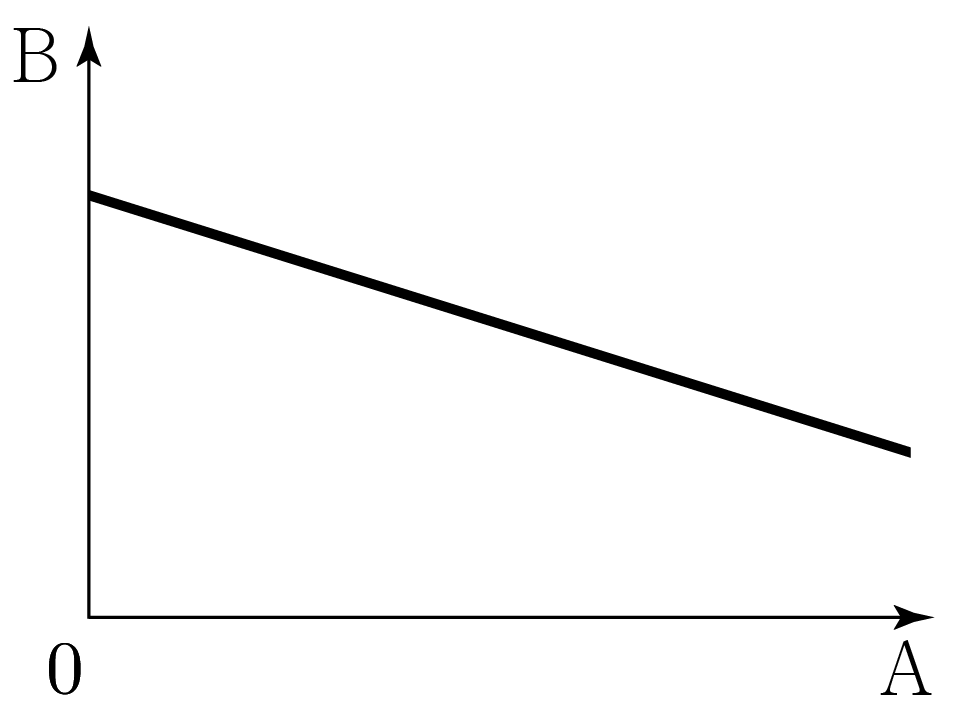
가로축은 조작 변인을 나타내고, 세로축은 종속 변인을 나타내므로 이 그래프는 실험자가 의도적으로 를 변화시킬 때, 이로 인해 가 변하는 것을 나타낸 것이다.
각 축에서 화살표 방향으로 갈수록 값이 커지므로 를 증가시키면 는 감소함을 알 수 있다.
¶ 생명과학의 탐구 방법
크게 귀납적 탐구 방법과 연역적 탐구 방법으로 나눌 수 있다.
¶ 귀납적 탐구 방법
자연 현상을 관찰하여 얻은 자료를 분석하여 일반적인 원리를 도출해내는 탐구 방법이다.
¶ 귀납적 탐구 과정
자연 현상의 관찰 → 관찰 주제의 선정 → 관찰 방법과 절차의 고안 → 관찰의 수행 → 관찰 결과 분석 → 결론 도출
¶ 귀납적 탐구 사례
핀치새의 부리의 귀납적 탐구 사례
자연 현상의 관찰: 갈라파고스 군도에 사는 핀치새의 부리 모양이 서로 다른 것을 발견했다.
관찰 주제의 선정: 다양한 환경에 서식하는 핀치의 부리를 관찰하기로 했다.
관찰 방법과 절차의 고안 + 관찰의 수행: 갈라파고스 군도의 각 섬에 사는 핀치를 관찰 및 채집한 후 부리 모양을 서로 비교했다.
관찰 결과 분석 + 결론 도출: 서식 지역과 먹이에 따라 핀치의 부리 모양이 달라졌다는 결론을 내렸다.
¶ 연역적 탐구 방법
잠정적인 답인 가설을 세우고 가설의 옳고 그름을 검증하는 탐구 방법이다. 가설은 옳고 그름이 확인 가능하도록 설정해야 한다.
¶ 연역적 탐구 과정
자연 현상의 관찰 → 문제 인식 → 가설 설정 → 탐구 설계 및 수행 → 결과 정리 및 분석 → 결론 도출(가설이 옳지 않을 경우 가설 설정으로 돌아가 가설 수정) → 일반화
¶ 연역적 탐구 사례
땀 분비의 연역적 탐구 사례
자연 현상의 관찰: 운동하면 심장이 빠르게 뛰는 것을 경험한다.
문제 인식: 운동을 하는 것과 심박수의 변화는 어떤 관계가 있을까?
가설 설정: 운동을 하면 심박수가 증가할 것이다.
탐구 설계 및 수행: 성별과 나이가 같은 참가자를 두 집단으로 나누어 초기 심박수를 측정하고, 집단별로 분 동안 아래의 행동을 수행시킨 후 다시 심박수를 측정한다.
- 대조군: 의 방에서 분 동안 가만히 앉아 있는다.
- 실험군: 의 방에서 분 동안 운동을 한다.
이 실험에서의 변인:
- 독립 변인:
• 조작 변인: 운동 여부
• 통제 변인: 성별, 나이, 방의 온도, 심박수 측정 간격 - 종속 변인: 심박수
결과 정리 및 분석: 운동을 한 집단에서 심박수가 증가하였다.
결론 도출: 운동을 하면 심박수가 증가한다. (가설이 옳다.)
일반화: 사람은 운동을 하면 심장이 더 빠르게 움직인다.
¶ 적용 문항
¶ 1번 문항

정답: $5$
ㄱ. 연역적 탐구는 가설을 세우고 가설의 옳고 그름을 검증하는 단계가 포함되어 있다.
자료에는 이 과정이 없으므로 연역적 탐구 방법이 이용되지 않았다.
자료에서는 불빛이 밝은 쪽에 더 많은 벌레가 모인다(자연 현상)는 것을 관찰하여 가설을 세우는 과정 없이 벌레는 강한 빛에 이끌리는 경향이 있다(일반적인 원리)는 것을 도출했으므로 귀납적 탐구 방법에 해당한다. (X)
ㄴ. 변인 통제는 대조 실험에서 조작 변인을 제외한 다른 모든 독립 변인을 일정하게 유지하는 것이므로 ⓐ는 변인 통제 과정에 해당한다. (O)
ㄷ. (라)에서 결론을 내렸으므로 (라)는 탐구 과정 중 결론 도출 단계에 해당한다. (O)
따라서 정답은 번이다.
¶ 2번 문항

정답: $3$
ㄱ. 연역적 탐구는 가설을 세우고 가설의 옳고 그름을 검증하는 단계가 포함되어 있다.
자료에는 (가)에서 가설을 세우는 단계가 있으므로 연역적 탐구 방법이 이용되었다. (O)
ㄴ. 조작 변인은 실험에서 의도적으로 변화시키는 변인이고, 자료에서 과 가 받는 햇빛의 양을 의도적으로 변화시키고 있으므로 ⓐ(햇빛)는 조작 변인이다. (O)
ㄷ. (라)에서 햇빛을 받으면 식물이 더 잘 자란다는 결론을 내렸으므로 어두운 곳에 둔 가 햇빛이 잘 드는 곳에 둔 보다 잎이 적고 줄기 높이가 낮아야 한다. 그러므로 ㉠, ㉡은 각각 , 이다. (X)
따라서 정답은 번이다.


